基于改进SVR算法的灌浆功率阈值预测方法研究

王晓玲，薛林丽，佟大威，余 佳，祝玉珊，王佳俊

基于改进SVR算法的灌浆功率阈值预测方法研究

王晓玲，薛林丽，佟大威，余 佳，祝玉珊，王佳俊

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

灌浆过程中将灌浆功率控制于阈值范围之内，有利于保证灌浆安全和质量．目前施工现场多根据有限个原位点的灌浆生产性试验，结合专家经验确定灌浆功率阈值．为实现灌浆功率阈值的科学预测，本研究在三维精细裂隙网络模拟和支持向量回归(SVR)算法两方面提出了改进技术．前者采用改进的拉丁超立方抽样(ILHS)方法模拟出与实际分布拟合度更高的裂隙参数，从而可构建与岩体实际地质情况一致性更高的三维精细裂隙网络模型，基于建立的裂隙模型和灌浆实时监控与分析系统采集地质参数和施工参数来构建灌浆功率阈值预测模型的输入参数集，具体包括：裂隙数量、裂隙平均迹长、裂隙平均倾向、裂隙平均倾角、灌前透水率、孔序、孔深和设计压力．后者采用改进蝗虫优化算法(IGOA)对SVR算法进行改进，实现对惩罚因子、核参数以及不敏感损失系数的优化计算，其中IGOA中通过引入混沌理论、动态权重和Lévy飞行以弥补算法易陷入局部最优的不足，提高算法的搜索能力．基于IGOA-SVR算法构建了灌浆功率阈值预测模型，可实现各灌浆孔孔段的灌浆功率阈值高精度预测．将所提出的算法和预测模型应用于西南某水电站灌浆工程灌浆功率阈值的预测分析，通过与4种常用的预测模型进行对比，表明其比现有常用模型具有更高的精度．

灌浆功率阈值；三维精细裂隙网络；拉丁超立方抽样方法；蝗虫优化算法；支持向量回归

灌浆能够显著降低坝基渗透能力，提高岩体稳定性和密实性[1]，因此保证灌浆质量对于维持建筑物的安全、长久、稳定运行具有重要意义．张海军等[2]和熊义泳等[3]通过对实际工程进行分析，指出灌浆过程中岩体的抬动变形与灌浆压力和注入率的共同作用联系紧密，灌浆压力过大或注入率过大都有可能引发坝基抬动．灌浆过程中灌浆压力和注入率相互联系和制约，将两者联合调控是灌浆质量控制的关键措施[4].夏可风[5]指出灌浆过程中维持灌浆功率(其数值等于灌浆压力和注入率的乘积)的基本恒定能够有效保证灌浆安全和质量．樊启祥等[6]基于夏可风灌浆功率法，提出水泥灌浆三区五阶段智能控制模型iGCM，其核心概念是灌浆过程中控制灌浆功率位于阈值范围之内，避免出现灌浆不充分或有害岩体破坏等不良状况，已有的工程实践结果表明iGCM具有良好的应用前景．综上所述，灌浆功率阈值可以为灌浆过程中灌浆功率的调控提供标准，准确有效的灌浆功率阈值确定方法尤为重要，但目前施工现场通常基于有限个先导孔的灌浆生产性试验并结合专家经验确定灌浆功率阈值．因此，开展灌浆功率阈值预测研究具有重要意义．

近年来，随着智能技术的快速发展，智能算法已广泛应用于灌浆工程领域．然而，现有预测研究多侧重于可灌性[7-9]、注灰量[10-11]、灌后质量等[12]指标，未见对灌浆功率阈值的预测研究报道．支持向量回归(support vector regression，SVR)作为支持向量机(support vector machine，SVM)的一种拓展，对具有小样本、高维、非线性特征的问题具有很好的适应性，目前已广泛应用于工程领域[9,13]，因此可以将其应用于灌浆功率阈值预测研究．同时，地质条件的复杂性造成每个灌浆孔孔段的灌浆功率阈值存在差异，因此需要根据每个灌浆孔孔段各自的特征建立不同的预测模型，本文基于三维精细裂隙网络模型和灌浆实时监控与分析系统采集每个灌浆孔孔段特有的地质参数和施工参数构建预测模型的输入参数集，具体包括：裂隙数量、裂隙平均迹长、裂隙平均倾向、裂隙平均倾角、灌前透水率、孔序、孔深以及设计压力．但在预测模型建立过程中，会面临以下两个问题：①建立三维精细裂隙网络模型时，目前常利用随机抽样方法对裂隙参数进行模拟，但是，如何在有限抽样的情况下保障抽样的代表性仍是一个难题；②SVR模型的预测性能很大程度上受参数(惩罚因子)、(核参数)、(不敏感损失系数)的影响，因此，准确地确定参数是预测模型结果好坏的关键．传统依靠人工经验给定参数值的方法效率低、主观性大[14]，一些常用的优化算法存在易陷入局部最优的不足，如何保证预测结果的准确性还存在困难．

综上所述，为解决当前施工现场通常根据有限个先导孔的灌浆生产性试验并结合专家经验确定灌浆功率阈值时存在信息不足和主观性大等方面的问题，本文构建了一种基于IGOA-SVR算法的灌浆功率阈值预测模型，在充分考虑每个灌浆孔孔段特有的地质参数和施工参数的基础上，实现各灌浆孔孔段灌浆功率阈值的准确预测．针对问题①，提出改进的拉丁超立方抽样(improved Latin hypercube sampling，ILHS)方法，利用该方法可提高抽样的代表性，从而获得更加符合实际情况的裂隙参数，使建立的三维裂隙网络模型更加贴合实际地质状况；针对问题②，基于蝗虫优化算法(grasshopper optimization algorithm，GOA)原理简单、调节参数少的优点，提出耦合混沌理论、动态权重和Lévy飞行的改进蝗虫优化算法(improved grasshopper optimization algorithm，IGOA)以避免算法陷入局部最优，从而对SVR模型参数优化问题进行求解．基于IGOA-SVR算法的预测模型能够实现灌浆功率阈值高精度预测，从而为实际灌浆施工提供有效的理论指导．

1 预测模型框架

本文构建的基于IGOA-SVR算法的灌浆功率阈值预测模型主要包括3部分：参数层，方法层，应用层．框架如图1所示．

在参数层，基于三维精细裂隙网络模型和灌浆实时监控与分析系统获取各个灌浆孔孔段地质参数及施工参数．其中，三维精细裂隙网络模型采用本文提出的基于改进拉丁超立方抽样的三维精细裂隙网络模型建模方法建立．

在方法层，提出一种具有高精度的算法来建立模型：①利用混沌理论初始化GOA种群，增强种群的多样性，使得解更均匀地遍布在搜索空间内；②在蝗虫位置更新公式中引入动态权重，保证全局探索能力的同时，提高了收敛速度；③采用Lévy飞行更新GOA种群，有利于增强全局搜索能力，提高找到最优解的概率．应用提出的具有强搜索能力的IGOA对SVR模型的惩罚因子、核参数和不敏感损失系数进行参数优化，进而构建基于IGOA-SVR算法的灌浆功率阈值预测模型，实现各个灌浆孔孔段的灌浆功率阈值高精度预测．

在应用层，将预测模型应用于实际工程中进行检验．本文将预测模型应用于西南某水电站固结灌浆工程中，并与4种常用的预测模型进行对比分析，验证了本文模型的准确性．

图1 预测模型框架

2 灌浆功率阈值预测数学模型与方法

2.1 灌浆功率阈值预测数学模型

灌浆功率阈值预测的数学模型如图2所示：包括目标函数集、模型输入参数集和方法集．其中，式①定义了预测模型的目标函数，表示灌浆功率阈值(灌浆功率下临界值l，灌浆功率上临界值u)与预测输入参数集之间的复杂关系．式②定义了预测模型的输入参数集，包括地质参数和施工参数在内的8个输入参数，具体包括裂隙数量1、裂隙平均迹长2(m)、裂隙平均倾向3(rad)、裂隙平均倾角4(rad)、灌前透水率5(Lu)、孔序6、孔深7(m)和设计压力8(MPa)，其中基于三维精细裂隙网络模型获取1、2、3、4，基于灌浆实时监控与分析系统获取5、6、7、8．式③和式④定义了求解目标函数的方法集IGS，其中包括混沌初始化、动态权重()、Lévy飞行()和GOA组合形成的IGOA以及支持向量回归(SVR)算法．IGOA用于优化SVR模型的参数，IGS用于灌浆功率阈值预测分析．

图2 灌浆功率阈值预测数学模型

2.2 灌浆功率阈值预测方法

2.2.1 输入参数获取方法

灌浆功率阈值受多种因素的影响，其中地质参数和施工参数是主要的影响因素．由于地质条件的复杂性和隐蔽性，难以全面获取各灌浆孔孔段的地质状况，因此本研究结合三维精细裂隙网络模型获取与每个灌浆孔孔段相交的裂隙数量、裂隙平均迹长、裂隙平均倾向、裂隙平均倾角，与此同时，基于灌浆实时监控与分析系统获取灌前透水率、孔序、孔深和设计压力．集成上述所有参数，可构建输入参数集．

与传统意义上的等效多孔介质(equivalent porous media，EPM)模型不同，离散裂隙网络(discrete fracture network，DFN)模型明确定义了模拟区域内每一条裂隙的位置、产状、几何形态、尺寸、宽度以及孔渗性质等，同时对裂隙进行分组，每一组均有各自的统计学共性，因此所有裂隙在空间上既被相互独立地随机放置，又分别属于不同发育特征的裂隙组．这种处理方式保证了裂隙网络被当作离散对象来对待，同时各种性质的裂隙参数都能得到充分考虑，因而为获得精确的裂隙几何模型与裂隙参数模型提供了可能．

利用DFN模型建立三维精细裂隙网络模型[15]的具体流程为：①原始数据勘探与统计；②统计均质区划分；③裂隙优势分组；④裂隙几何参数分布类型确定；⑤裂隙几何参数随机抽样；⑥利用三维建模软件建立三维裂隙网络模型．其中，应用有效的抽样方法对裂隙几何参数进行抽样对于保证三维裂隙网络模型与实际地质状况的高一致性具有重要意义．目前常用的随机抽样方法有Monte Carlo方法[1]、LHS方法等[15]，上述方法虽然能够取得较好的抽样结果，但仍具有一定的不足．Monte Carlo方法抽样结果精度低、稳定性差，且易出现样本坍塌等[16]不良情况，需进行大量抽样才能得到较好的抽样结果；LHS方法作为一种分层抽样方法，虽在一定程度上克服了Monte Carlo方法的不足，但因其将参数区间均分后，在每个子区间中的抽样个数相同，与参数实际分布情况存在一定的差异，因此本文提出一种改进的拉丁超立方抽样(ILHS)方法．该方法依据参数实际分布情况确定在每个子区间中抽取的样本个数，保证抽样结果与实际情况统计规律的一致性，为准确建立三维精细裂隙网络模拟提供了可靠手段．LHS方法计算流程 如下．

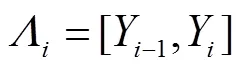
ILHS方法在LHS方法的基础上，根据参数实际分布情况确定任意子区间[-1，]内需抽取样本的个数，具体公式为

式中：为该组裂隙随机模拟数量；为采集到的实际裂隙数量；为分布函数位于子区间[-1，]内所对应的参数的数量．

2.2.2 IGOA-SVR算法

SVR作为SVM的拓展，由Drucker等[17]提出，可用于解决非线性回归问题，但其回归精度很大程度上受参数、、的影响，常采用优化算法对参数进行优化．

蝗虫优化算法是Mirjalili于2017年提出的一种模拟真实蝗虫觅食行为的群体智能优化算法，该算法参数少、易于实现，且具有较强的全局搜索能力和局部搜索能力，目前已成功应用于产品的优化配置[18]、参数优化[19]等各类优化问题，算法的具体流程可参考文献[20]．蝗虫优化算法GOA通过种群之间的相互作用不断向目标靠近，但该过程同时导致种群多样性降低，从而易使算法陷入局部最优．为进一步提高GOA的寻优性能，使其更有效地解决SVR模型参数优化问题，本文以标准GOA为基础，通过引入混沌理论、动态权重和Lévy飞行，构建了改进蝗虫优化算法．

首先，采用混沌理论初始化种群．混沌运动具有遍历性、随机性和规律性等特点，利用混沌的良好特性初始化GOA蝗虫位置，提高种群多样性，避免早熟收敛[21]．采用Tent混沌映射初始化种群的流程如下.

(1)将搜索空间映射到[0，1]空间．

(2)采用Tent混沌映射生成混沌序列．

(3)将混沌序列映射到解的搜索空间．

应用Tent混沌映射初始化GOA种群，GOA蝗虫个体能更好地遍历整个搜索空间，提高算法找到最优解的概率．

其次，在种群更新中引入动态权重．在GOA搜索后期，种群不断向目标位置靠近，但收敛速度  慢[22]，因此在算法更新公式中引入动态权重[23]，在保证全局探索能力的同时，提高了收敛速度．标准GOA按式(5)进行蝗虫位置更新．

本次设计的最大工作负压为55 kPa，气体流量为50 m3/min，砂粒的运输距离大于15 m.常见真空源难以同时满足以上要求，经过考察选择了韩国KFM公司的逆流冷却式罗茨真空泵，型号为ST250SVBF，其性能参数如表1.

式中：为收敛因子；NP为种群数目；ub和lb分别为第维上的搜索上界和下界；为吸引力函数；d为第只蝗虫和第只蝗虫之间的距离，为目前最佳解所对应的第维的位置．

在式(5)中引入动态权重之后，蝗虫位置更新数学表达式为

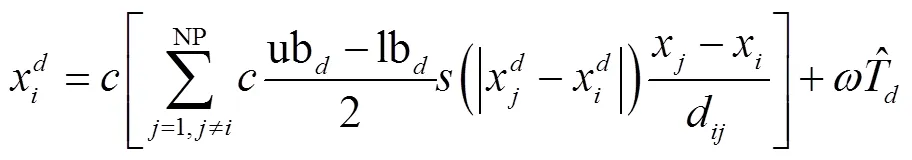
式中：为动态权重；max为最大值；min为最小值；为当前迭代；Max_iter为最大迭代次数．

此外，在搜索过程中，Lévy飞行可以大部分时间内小范围活动，小部分时间内进行大范围的跳跃，并且运动方向完全随机化[24-25]，这与自然界动物的觅食过程相似．应用Lévy飞行对GOA的种群更新公式进行改进，有利于算法跳出局部最优，增强全局搜索能力．数学表达式如下：

式中：rand为介于区间[0，1]之间的随机数；Lévy的具体定义可参照文献[26]．

IGOA通过耦合混沌理论、动态权重和Lévy飞行以提高初始化种群多样性，同时增强了算法的全局和局部搜索能力，收敛速度更快，在理论上具有更高的收敛精度，因此，选用IGOA对SVR模型参数进行优化．

为了验证该算法的有效性与优越性，借助一些测试函数对算法进行测试以验证该算法在精度、稳定性等方面的优势，其中1、2、3为单峰测试函数，4、5和6为多峰测试函数，测试结果如表1所示．

由表1可知，IGOA对于选取的所有测试函数寻优的最优值、均值和方差均低于GOA，表明在有限的迭代次数下，IGOA的收敛精度和输出结果稳定性更高，因此，本文提出的IGOA具有更强的寻优性能，能够有效地解决SVR模型的参数优化问题．IGOA-SVR预测方法流程如图3所示．

表1 测试函数的结果

Tab.1 Test function results

注：以上结果来自GOA和IGOA独立运行30次

图3 IGOA-SVR方法流程

3 结果分析与讨论

3.1 数据收集及处理

为获取全面的地质参数，从而精确地反映坝基复杂地质状况对灌浆功率阈值的影响，需建立坝基岩体三维精细裂隙网络模型．基于揭露面裂隙素描图及钻孔图像等资料对裂隙各几何参数进行统计；然后利用Baecher圆盘模型对裂隙进行表达，基于统计学方法和体视学方法确定裂隙位置、迹长、产状的概率分布类型及各组裂隙的数量之后，采用ILHS方法对裂隙各几何参数进行抽样并随机组合，经过误差检验得到研究区域裂隙模拟参数；最后利用三维可视化建模软件建模得到三维裂隙网络模型，并获取与各个灌浆孔孔段相交裂隙的数量、平均迹长、平均倾向和平均倾角．其中某一个灌浆孔孔段的示意图如图4所示，有4条裂隙与该孔段相交，其平均迹长、平均倾向和平均倾角分别为1.05m、22.04°、153.57°．

其次，基于灌浆实时监控与分析系统采集灌前透水率和施工参数，集成地质参数和施工参数构建灌浆功率阈值预测输入参数集．

图4 基于三维精细裂隙网络模型获取地质参数示意

3.2 结果分析

首先设置IGOA种群数量为30，最大迭代次数为100，待优化参数、、的寻优范围分别为[1，1000]、[0，10]和[0，0.2]；其次将260组数据划分为训练集(210组数据)和测试集(50组数据)，完成数据归一化后采用IGOA对SVR模型参数寻优，进而得到训练完成的SVR模型；最后，基于得到的SVR模型对灌浆功率阈值进行预测，如图5所示．

由图5可知，通过本文建立的IGOA-SVR预测模型得到的灌浆功率阈值的预测值与实测值基本保持一致，其中下临界值预测模型的RMSE、MAPE、MAE和EC分别为0.7531MPa·L/min、8.1122%、0.4776MPa·L/min和0.9622，上临界值预测模型的RMSE、MAPE、MAE和EC分别为1.5107 MPa·L/min、8.1583%、0.9658MPa·L/min、0.9618，各项评价指标均处于较低水平，表明该模型具有较好的预测性能，能够用于灌浆功率阈值预测分析．

图5 基于IGOA-SVR算法的灌浆功率阈值预测结果

3.3 对比分析及讨论

3.3.1 ILHS方法优越性讨论

为说明本文提出的ILHS方法的优越性，将其与LHS进行对比，并利用相对误差对抽样结果进行检验．根据裂隙产状参数将研究区域内采集到的实测裂隙分为4组，由于篇幅所限，本文仅列出第4组裂隙参数的统计结果和模拟对比情况．裂隙参数的统计结果如表2所示．建立的三维裂隙网络模型如图6所示，其中(a)、(b)为两种方法的三维模型对比图，(c)、(d)为两种模型揭露面位置裂隙分布情况．揭露面位置裂隙素描图与三维裂隙网络模型对应位置处的二维图如图7所示．

表2 裂隙参数统计分析结果

Tab.2 Statistical analysis results of fracture parameters

图6 不同抽样方法3D建模对比(以第4组为例)

图7 不同抽样方法建模2D剖面与裂隙素描图对比(以第4组为例)

由图6可知，分别利用LHS方法和ILHS方法获得的裂隙在空间上分布均匀，产状趋势合理．由图7可知，虽然两种方法获得的揭露面上的裂隙分布情况和原始裂隙素描图上的裂隙分布情况存在差异，但总体趋势与真实分布接近，并且应用ILHS方法得到的裂隙模型比应用LHS方法得到的裂隙模型与实际分布情况的一致性更高．

表3为揭露面实测数据与模型数值对比分析结果，结果表明，基于ILHS方法抽取的裂隙参数建立的三维裂隙模型在对应揭露面上的参数统计结果总体优于基于LHS方法获得的裂隙模型，与实测值统计结果更为接近，进一步表明ILHS方法的优越性．应用ILHS方法最终建立的三维精细裂隙网络模型如图8所示．

表3 揭露面实测值与模拟值对比

Tab.3 Comparison of measured and simulated results of the exposed surface layer

图8 基于ILHS建立的三维精细裂隙网络模型

3.3.2 IGOA-SVR算法优越性讨论

为了验证本文方法预测精度的优越性，将所提出的方法与目前常用的多元线性回归(multiple linear regression，MLR)、BP神经网络(BPNN)、SVR以及标准GOA优化SVR算法(GOA-SVR)预测方法进行对比，采用均方根误差(RMSE)、平均绝对百分比误差(MAPE)、平均绝对误差(MAE)和等系数(EC)[27-28]作为误差评价指标．预测结果对比如图9所示，误差分析结果对比如表4和表5所示，根据图9和表4、表5得到如下对比分析结论．

图9 5种方法预测结果对比

由图9可知，5种方法均能够较精确地预测出灌浆功率阈值．此外，由表4可知，在灌浆功率下临界值预测方面，本文方法的RMSE、MAPE、MAE分别为0.7531MPa·L/min、8.11%和0.4776MPa·L/ min，较GOA-SVR预测方法分别降低了1.44%、4.27%和4.99%，同时本文方法的EC为0.9622，较GOA-SVR预测方法提高了0.21%；由表5可知，在灌浆功率上临界值预测方面，本文方法的RMSE、MAPE和MAE分别为1.5107MPa·L/min、8.16%和0.9658MPa·L/min，较GOA-SVR预测方法分别降低了2.02%、2.97%和4.75%，EC为0.9618，较GOA-SVR预测方法提高了0.20%，上述表明IGOA通过引入混沌理论、动态权重和Lévy飞行，克服了GOA易陷入局部最优的不足，具有更好的寻优性能，从而保证了预测模型的精度．此外，相较于多元线性回归(MLR)、BP神经网络(BPNN)以及SVR方法，本文提出的灌浆功率阈值预测方法的RMSE、MAPE以及MAE均最小，EC最大，进一步表明本文方法在预测精度上的优越性．

表4 灌浆功率下临界值误差分析结果

Tab.4 Error analysis results of lower grout-power limit

表5 灌浆功率上临界值误差分析结果

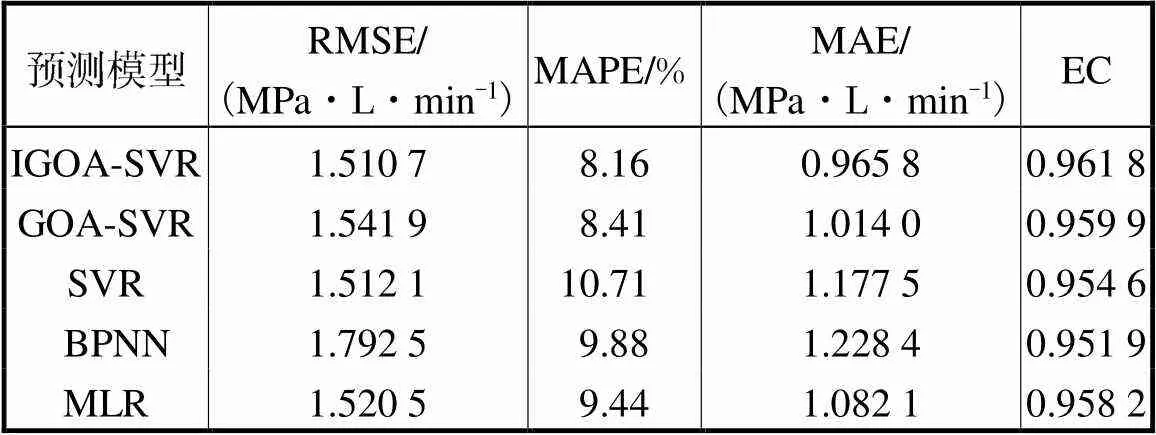
Tab.5 Error analysis results of upper grout-power limit

综上，本文在结合SVR算法能够有效处理高维、非线性、小样本问题的基础上，集成IGOA参数少、收敛速度快、搜索能力强的优势，构建了IGOA-SVR灌浆功率阈值预测模型，能取得较高的预测精度．灌浆施工前，进行灌浆功率阈值的有效预测，可为灌浆过程中灌浆功率的调控提供控制标准，从而为保证灌浆过程的安全稳定提供可能．

4 结 论

目前多根据原位点的灌浆生产性试验并结合专家经验确定灌浆功率阈值，为实现灌浆功率阈值的高精度预测，本文构建了一种基于改进支持向量回归算法的灌浆功率阈值预测模型，主要结论如下：

(1)提出了改进拉丁超立方抽样ILHS方法，可提高抽样的代表性，从而获得更加符合实际情况的裂隙参数，使建立的三维裂隙网络模型更加贴合实际地质状况；

(2)提出了改进蝗虫优化算法IGOA，避免算法陷入局部最优，从而对SVR模型参数优化问题进行求解；

(3)综合利用ILHS方法和IGOA-SVR模型构建的灌浆功率阈值预测模型能够实现高精度预测，具有较好的实用性．

［1］ 敖雪菲，王晓玲，赵梦琦，等. 坝基裂隙岩体三维灌浆数值模拟[J]. 水利学报，2017，48(8)：945-954.

Ao Xuefei，Wang Xiaoling，Zhao Mengqi，et al. Three-dimensional grouting simulation in fractured rock mass of the dam bedrock[J]. Journal of Hydraulic Engineering，2017，48(8)：945-954(in Chinese).

［2］ 张海军，张树军，张 岩. 灌浆施工中砼盖板抬动成因分析及处理[J]. 河南科学，2003，21(2)：243-246.

Zhang Haijun，Zhang Shujun，Zhang Yan. The formation and treatment of concrete coverboard in grouting construction[J]. Henan Science，2003，21(2)：243-246(in Chinese).

［3］ 熊义泳，孙忠明，姚文武. 清江水布垭电站现场帷幕灌浆试验与分析[J]. 岩石力学与工程学报，2004，23(9)：1558-1563.

Xiong Yiyong，Sun Zhongming，Yao Wenwu. The formation and treatment of concrete coverboard in grouting construction[J]. Chinese Journal of Rock Mechanics and Engineering，2004，23(9)：1558-1563(in Chinese).

［4］ Strømsvika H，Grøv E. Interpretation of pressure and flow during pre-grouting in hard rock tunneling[C]//5th International Conference on Grouting，Deep Mixing，and Diaphragm Walls. Honolulu，America，2017(287)：285-294.

［5］ 夏可风. 夏可风灌浆技术文集[M]. 北京：中国水利水电出版社，2015.

Xia Kefeng. Grouting Technology Collected Works[M]. Beijing：China Water and Power Press，2015(in Chinese).

［6］ 樊启祥，黄灿新，蒋小春，等. 水电工程水泥灌浆智能控制方法与系统[J]. 水利学报，2019，50(2)：165-174.

Fan Qixiang，Huang Canxin，Jiang Xiaochun，et al. Intelligent grouting control method and system for hydropower engineering[J]. Journal of Hydraulic Engineering，2019，50(2)：165-174(in Chinese).

［7］ Cheng M Y，Hoang N D. Groutability prediction of microfine cement based soil improvement using evolutionary LS-SVM inference model[J]. Journal of Civil Engineering and Management，2014，20(6)：839-848.

［8］ Hoang N D，Tien B D，Liao K W. Groutability estimation of grouting processes with cement grouts using differential flower pollination optimized support vector machine[J]. Applied Soft Computing，2016，45：173-186.

［9］ Deng Shaohui，Wang Xiaoling，Zhu Yushan，et al. Hybrid grey wolf optimization algorithm-based support vector machine for groutability prediction of fractured rock mass[J]. Journal of Computing in Civil Engineering，2019，33(2)：04018065.1-04018065.9.

［10］ Fan Guichao，Zhong Denghua，Wang Jiajun，et al. Cement take evaluation and prediction based on empirical relationships and support vector regression[C]// International Conference on Energy & Environmental Protection. Shenzhen，China，2016：699-704.

［11］ Öge İ F. Prediction of cementitious grout take for a mine shaft permeation by adaptive neuro-fuzzy inference system and multiple regression[J]. Engineering Geology，2017(228)：238-248.

［12］ Li Xiaochao，Zhong Denghua，Ren Bingyu，et al. Prediction of curtain grouting efficiency based on ANFIS [J]. Bulletin of Engineering Geology and the Environment，2019，78(1)：281-309.

［13］ 贺玉琪，王 栋，王远坤. BRR-SVR月降水量预测优化模型[J]. 水利学报，2019，50(12)：1529-1537.

He Yuqi，Wang Dong，Wang Yuankun. BRR-SVR optimization model for monthly precipitation prediction[J]. Journal of Hydraulic Engineering，2019，50(12)：1529-1537(in Chinese).

［14］ Wang Jiajun，Zhong Denghua，Wu Binping，et al. Evaluation of compaction quality based on SVR with CFA：Case study on compaction quality of earth-rock dam[J]. Journal of Computing in Civil Engineering，2018，32(3)：05018001.1-05018001.10.

［15］ 岳 攀，钟登华，吴 含，等. 基于LHS的坝基岩体三维裂隙网络模拟[J]. 水力发电学报，2016，35(10)：93-102.

Yue Pan，Zhong Denghua，Wu Han，et al. Simulations of 3-D fracture networks in rock mass of dam foundation using Latin hypercube sampling[J]. Journal of Hydroelectric Engineering，2016，35 (10)：93-102(in Chinese).

［16］ Janssen H. Monter-Carlo based uncertainty analysis：Sampling efficiency and sampling convergence[J]. Reliability Engineering & System Safety，2013，109 (2)：123-132.

［17］ Drucker H，Burges C，Kaufman L，et al. Support vector regression machines[J]. Advances in Neural Information Processing Systems，1997，28(7)：779-784.

［18］ Gampa S R，Jasthi K，Goli P，et al. Grasshopper optimization algorithm based two stage fuzzy multiobjective approach for optimum sizing and placement of distributed generations，shunt capacitors and electric vehicle charging stations[J]. Journal of Energy Storage，2020，27：101117.

［19］ Heshmati M，Noroozian R，Jalilzadeh S，et al. Optimal design of CDM controller to frequency control of a realistic power system equipped with storage devices using grasshopper optimization algorithm[J]. ISA Transactions，2020，97：202-215.

［20］ Saremi S，Mirjalili S，Lewis A. Grasshopper optimisation algorithm：Theory and application[J]. Advances in Engineering Software，2017，105：30-47.

［21］ 董 娜，常建芳，吴爱国. 基于融合算法优化的卷积神经网络预测方法[J]. 天津大学学报：自然科学与工程技术版，2019，52(9)：990-998.

Dong Na，Chang Jianfang，Wu Aiguo. Convolution neural network prediction method based on the chaotic hybrid algorithm[J]. Journal of Tianjin University：Science and Technology，2019，52(9)：990-998 (in Chinese)

［22］ 高 增，张焕龙，陈宜滨，等. 基于动态权重蚱蜢优化算法的突变运动跟踪[J]. 郑州大学学报：理学版，2020，52(2)：36-44.

Gao Zeng，Zhang Huanlong，Chen Yibin，et al. Abrupt motion tracking based on dynamic weight grasshopper optimization algorithm[J]. Journal of Zhengzhou University：Natural Science Edition，2020，52(2)：36-44(in Chinese).

［23］ Teng Zhijun，Lü Jinling，Guo Liwen. An improved hybrid grey wolf optimization algorithm[J]. Soft Computing，2019，23(15)：6617-6631.

［24］ 高宏进，王 力. 一种基于动态惯性权重的鸟群优化算法[J]. 计算机应用研究，2019，36(5)：1376-1379，1384.

Gao Hongjin，Wang Li. Bird swarm algorithm based on dynamic inertia weight[J]. Application Research of Computers，2019，36(5)：1376-1379，1384(in Chinese).

［25］ 朱 迪，梅亚东，许新发，等. 复杂防洪系统优化调度的三层并行逐步优化算法[J]. 水利学报，2020，51(10)：1199-1211.

Zhu Di，Mei Yadong，Xu Xinfa，et al. Triple parallel progressive optimality algorithm for optimal operation of the complicated flood control system[J]. Journal of Hydraulic Engineering，2020，51(10)：1199-1211(in Chinese).

［26］ Viswanathan G M，Afanasyev V，Buldyrev S V，et al. Lévy flight search patterns of wandering albatrosses[J]. Nature，1996，381(6581)：413-415.

［27］ Li Yanfei，Shi Huipeng，Han Fengze，et al. Smart wind speed forecasting approach using various boosting algorithms，big multi-step forecasting strategy[J]. Renewable Energy，2018，135：540-553.

［28］ Tian Xiujuan，Yu Dexin，Xing Xue，et al. Hybrid short-term traffic flow prediction model of intersections based on improved complete ensemble empirical mode decomposition with adaptive noise[J]. Advances in Mechanical Engineering，2019，11(4)：16878140198418 1.1-168781401984181.15.

Grout Power Threshold Prediction Method Based on Improved SVR Algorithm

Wang Xiaoling，Xue Linli，Tong Dawei，Yu Jia，Zhu Yushan，Wang Jiajun

(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

In the grouting process，the grout power should be controlled within the threshold to ensure the safety and quality of the grout. Currently，the grout power threshold is determined based on the results of finite in-situ grout tests combined with the experience of experts. To scientifically predict the grout power threshold，in this paper，we propose two improved techniques for three-dimensional fine fracture simulation and a support vector machine(SVR) algorithm. To construct a 3D fine fracture network model that is more consistent with the actual geological condition of the rock mass，the proposed simulation involves improved Latin hypercube sampling(ILHS)to simulate fracture parameters that have a high degree of fitting with the actual situation. Based on the constructed 3D fine fracture network model and a real-time grout monitoring and analysis system，geological and construction parameters are established to construct a set of predictive input parameters for the grout power threshold prediction model. These parameters include the number of fractures，the average trace length of fractures，the average dip direction of fractures，the average dip angle of fractures，water permeability before grouting，hole sequence，hole depth，and design pressure. Improvement is realized by a proposed improved grasshopper optimization algorithm(IGOA) to optimize the penalty factor，the kernel function parameter，and the insensitive loss functionof the SVR algorithm. The IGOA is coupled with the chaos theory，dynamic weight，and Lévy flight to prevent it falling into a local optimum and to improve the search ability. Based on the IGOA-SVR algorithm，a grout power threshold prediction model is constructed that achieves high prediction accuracy. As a case study，the proposed algorithm and prediction model are applied to a prediction analysis of the grout power threshold of a hydropower station in Southwest China. A comparison with the results of four prediction models shows that the proposed model has higher accuracy than existing conventional models.

threshold of grout power；3D fine fracture network；Latin hypercube sampling；grasshopper optimization algorithm；support vector regression

TV543

A

0493-2137(2021)08-0771-10

10.11784/tdxbz202011018

2020-11-10；

2021-01-07.

王晓玲（1968—  ），女，博士，教授，wangxl@tju.edu.cn.

佟大威，tongdw@tju.edu.cn.

国家重点研发计划资助项目(2018YFC0406704)；国家自然科学基金资助项目(51839007，51679165).

Supported by the National Key Research and Development Program of China(No.2018YFC0406704)，the National Natural Science Foundation of China (No.51839007，No. 51679165).

(责任编辑：樊素英)