间歇性循环荷载条件下饱和重塑黏土的动力特性试验

雷华阳，杨晓楠，许英刚，张 磊

间歇性循环荷载条件下饱和重塑黏土的动力特性试验

雷华阳1, 2, 3，杨晓楠1，许英刚1，张 磊1

(1.天津大学建筑工程学院，天津 300350；2. 滨海土木工程结构与安全教育部重点实验室，天津 300350；3. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室，天津 300350)

针对运营期地铁列车荷载引起地基的长期沉降，以往三轴试验主要考虑了围压和固结比等对软土长期动力特性的影响，但在模拟地铁列车荷载时忽视了其周期性间歇的特点．基于此，本文针对天津地区饱和黏土开展了一系列间歇性循环荷载条件下的循环三轴不排水试验，分析了其对饱和黏土动应力-动应变关系、累积塑性应变及孔隙水压力发展的影响，并探讨了不同固结比和动应力比对轴向塑性累积应变的影响．研究结果表明：饱和黏土的动应力-动应变曲线的滞回形态随着振动阶段的增加逐渐向应变轴发展；黏土累积塑性应变随振动阶段发展逐渐增大且增长速率逐渐下降；由于土体滞后效应，在停振期部分累积塑性应变产生恢复，随着振次增加，各阶段残余应变值逐渐减小至一个稳定值；等压固结条件下的轴向塑性累积应变明显比偏压固结下的轴向塑性累积应变更大，同一固结条件下，轴向塑性累积应变随动应力比增大而增大；动孔压随振动阶段逐渐累积，而在前期振动循环阶段的停振阶段，累积动孔压出现略微增加；振动阶段后期部分，由于土体被压密表现为黏弹性，在停振期出现下降现象．

重塑黏土；间歇性循环荷载；滞后效应；动力特性

地铁是城市轨道交通系统中运用最广泛的铁路种类，具有用地省、运能大、准时舒适和安全环保等优点，在解决城市拥堵和环境污染问题中具有重要的作用，因此，被越来越多的大城市引入和使用．地铁列车荷载作为一种具有一定周期的长期循环振动荷载[1-2]，其对隧道周围土体力学特性的影响不容忽视，而这种影响与列车运行状态又有很大的相关性[3]．软土地区投付使用的地铁，会因各种原因产生工后长期沉降，如上海地铁1号线自运营以来最大沉降速率为40mm/年，局部路段沉降量达200mm[4]；广州地铁2号线自开通以来的最大沉降速率为40mm/年，最大不均匀沉降量达30mm[5]．

地铁列车循环荷载引起的软土地基长期沉降主要由土的累积塑性变形和超孔隙水压力消散引起，国内外学者对长期循环荷载作用下软土的变形特性研究进行了大量的工作．Andersen等[6]通过静、动三轴试验研究了波浪荷载对Drammen黏土静力特性的影响，结果表明正常固结黏土在循环荷载作用后表现出类似超固结性质．Yasuhara等[7]对Ariake重塑黏土进行的不排水强度和循环压缩试验结果表明，采用不同的应变破坏标准会使土体的动强度曲线有较大差别，并建立了循环荷载后强度变化的公式．Moses等[8]采用循环三轴剪切试验以研究应变效应和荷载循环对海相黏土不排水抗剪强度的影响，得出周期荷载会降低黏土的不排水强度，其不排水强度的衰减程度最大可达50%．唐益群等[9]对淤泥质粉质黏土进行了应力控制循环三轴试验，得到了土体在列车振动荷载作用下的临界动应力比以及动应变随振次、加载频率、围压的变化规律．黄茂松等[10]在典型饱和软黏土不排水循环三轴试验的基础上，分析了影响软黏土塑性累积变形的主要因素，研究了不同静、循环动应力组合应力历史影响下饱和软黏土的不排水循环累积变形特性．雷华阳等[11]研究了淤泥质粉质黏土在交通荷载长期作用下的动应变发展情况，得到了淤泥质粉质黏土的临界动应力比和动应力-动应变关系随加载频率、围压及固结状态而变化的规律．郑刚等[12]进行了一系列原状土和重塑土的动力试验，对比分析了振动频率对饱和黏土动力特性的影响．

针对运营期地铁列车荷载引起地基的长期沉降，循环三轴试验主要考虑了地铁列车荷载的幅值、频率、振动次数，以及围压和固结比对软土长期动力特性的影响，并取得了一定的成果．但以往研究中的室内试验在模拟地铁列车荷载时通常采取无间隔连续加载，忽视了地铁列车荷载的周期性间歇的特点[13].基于此，本文开展一系列间歇性循环荷载条件下的循环三轴不排水试验．考虑不同固结条件、动应力比和频率等因素，分析饱和黏土在不同加载阶段的动应力-动应变关系以及累积塑性应变和动孔隙水压力发展规律，通过与连续振动试验对比，分析间歇性循环加载对软土动力特性的影响．研究结果可为黏土地基在地铁行车荷载下的沉降预测提供理论参考．

1 试验土样和试验方案

1.1 试验土样

试验土样取自天津某地铁隧道附近，取土深度15～18m．依据《土工试验方法标准》(GB/T 50123—2019)采用击实法制备重塑土样试样，土样尺寸为高80mm、直径39.1mm的标准圆柱体，因动三轴试验所用试样尺寸与三瓣膜内径尺寸一致，故土样在三瓣膜内分5次击实，击实前在三瓣膜内壁涂抹一层薄的凡士林，确保土样与内壁相对光滑．根据三瓣膜体积与土体密度计算所需的土样总质量，然后用电子秤分5次称取平均每一层土样质量并放在三瓣膜内，每一层击实后用刨毛刀把表面刨毛，击实完毕后用刮土刀削掉顶部和底部多余土样，称其质量．最后用裁剪好的保鲜膜包裹试样四周，上下各贴一片滤纸，随后放入真空饱和器抽真空(－0.1MPa)，12h后，将蒸馏水缓慢注入至淹没三瓣膜顶，继续保持真空状态0.5h，关闭注水阀门，然后打开进气阀门使内部恢复大气压力，静置12h以上备用．试验时反压饱和时间120min，值达到0.95以上试样饱和．

表1 土样物理力学参数

1.2 试验方案

针对地铁列车荷载，目前常用的确定方法主要有现场测试分析法、人工激振力函数法、经验公式分析法及有限元模拟法．本文采用激振力函数法，所得车速120km/h时的地铁列车荷载时程曲线如图1所示. 试验循环加载波形如图2所示．具体试验参数见表2.

图1 地铁列车荷载的时程曲线

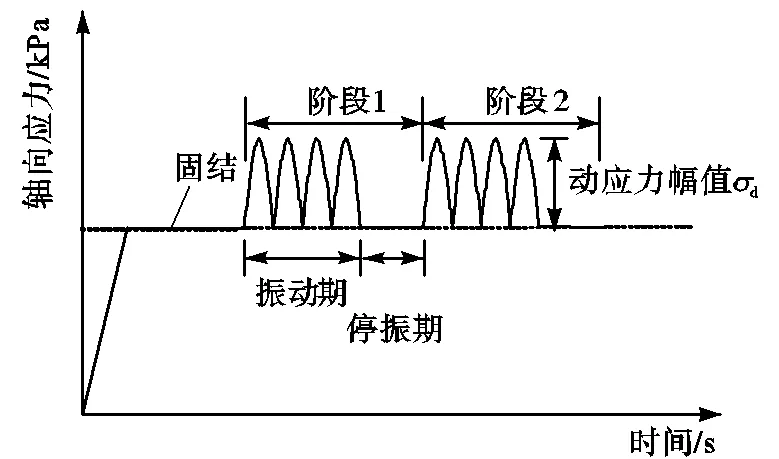
图2 试验循环加载波形示意

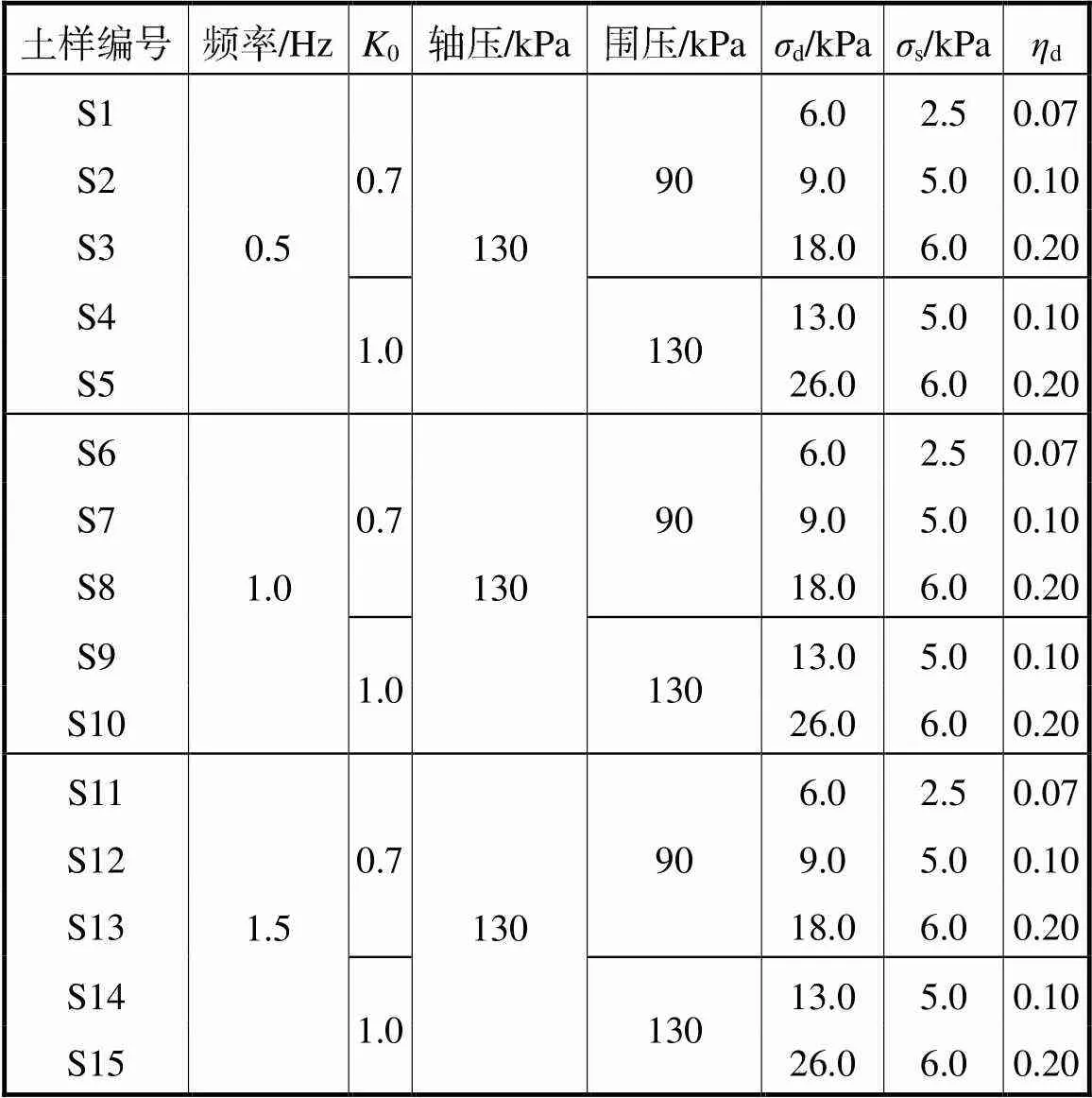
由图1可知，地铁列车循环荷载在地基中产生的动应力时程曲线具有“锯齿”状特点，循环荷载的1个振动周期约为0.65s，频率为1.54Hz，取1.5Hz，因此用试验荷载频率1.5Hz模拟120km/h的列车速度．为比较不同列车速度对土体动力特性的影响，试验取40km/h、80km/h和120km/h 3种典型列车速度．由40km/h列车速度计算的循环荷载振动周期约为2.05s，因此，用0.5Hz的试验荷载频率模拟平均时速40km/h的情况；同理，用1.0Hz的荷载频率模拟常规时速80km/h的情况．

对于埋深18m处的黏土，按其上覆土层的平均重度约为17.3kN/m3计算[14]，则估算其轴压约为131.4kPa，试验取130kPa．循环荷载采用偏压半正弦波[15]，可以作为简化波形较好地模拟列车循环荷载．

对土样分阶段施加循环振动荷载，共振动10个阶段，根据国内地铁列车运营普遍规律，按每班地铁列车通过地基某一点引起振动10次，每5min有1班车，每天运营15h计算，则地基某点一天内共振动1800次，故取每个阶段振动1800次，停振900次，然后继续振动下一阶段．试验采用等向固结和偏压固结两种方式，通过试样的物理力学参数，确定0分别取1.0和0.7．

表2 动三轴试验方案

Tab.2 Dynamic triaxial test parameters

2 试验结果分析

2.1 动应力-动应变关系

土体在一定的动应力作用下产生变形，滞回曲线可以表示土体在某一个循环内各时刻应力应变关系的全过程．针对频率为1.5Hz的振动荷载条件，如图3所示，选取试样S15的4个阶段，绘制振动加载过程中的部分振次的动应力-动应变曲线．可以看出，饱和黏土的动应力-动应变曲线具有典型的非线性和滞后性特征，对黏土进行加载当应力达到最大值时，变形仍未达到最大值；针对卸载阶段，在卸载达到稳定值时，由于应变滞后，当应力卸荷至最低值时，变形并未与应力同相位达到最小值，变形稳定点要滞后于应力稳定点，其滞回形态随着振动阶段的发展逐渐向应变轴靠拢．

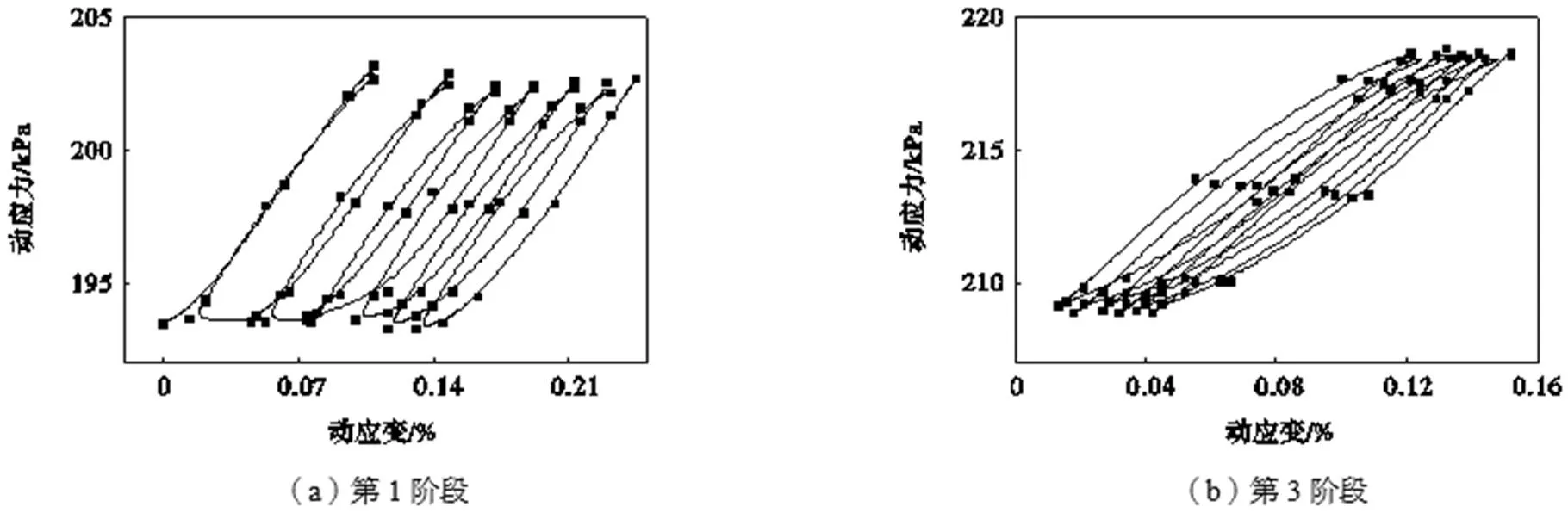
滞回曲线的不闭合程度可以反映每一个循环加载周期后残余应变的大小，从图3(a)可以看出，在振动初期，滞回曲线是不闭合的，产生大约0.01%的残余塑性变形，说明在地铁运营初期，隧道底部土体未压密区域在列车荷载作用下，迅速被压密，产生了一定的不可恢复残余变形，导致累积塑性变形迅速增加，整个阶段产生约0.14%的累积塑性变形．与图3(a)相比，随着振动阶段的增加，图3(b)中的滞回曲线底部开口变小很多，在此阶段的累积塑性变形约为0.05%，说明每个滞回圈的残余应变减小，导致累积塑性应变逐渐下降．滞回曲线的形状由“较宽”变为“瘦削”．对比图3(c)和(d)可以看出，滞回曲线几乎无明显变化，且每一振动周期内曲线尚未闭合但残余应变微小，因为此时振动次数已达10000次，土体已经被压密，变形很难进一步发展．

随着振动次数的不断增加，动应力-动应变曲线不断向右侧发展，滞回曲线不闭合程度越来越小，曲线由较为稀疏逐渐变为密实，说明塑性应变也逐渐减小，因为每一个振动循环内所产生的累积塑性应变已经趋于较小的稳定值．土体在动载作用下的变形常常包括弹性变形和塑性变形两部分，由于本文中试样的动应力幅值较小，试样主要表现为弹性变形，随着振次的增加，塑性变形逐渐产生和发展．

动应力-动应变曲线的倾斜程度反映出了动弹性模量的变化趋势，底部开口的大小可以反映出累积塑性应变的大小，基于此，可根据动应力-动应变关系曲线分别确定各阶段的动弹性模量和累积塑性应变，图4为试样S15动弹性模量及其平均残余塑性应变随振动阶段变化曲线，可以看出随着振动阶段的增加，动弹性模量和累积塑性应变总体上呈现下降的趋势，并最终趋于一个稳定值．第1阶段的残余应变值大约为0.145%，第3阶段急剧减少为0.052%，这与图3中滞回曲线底部开口由宽变为窄现象相符．随着振动阶段数的增加，第8阶段和第10阶段已趋于稳定，平均残余塑性应变仅为0.037%左右．说明随着阶段数的增加，土体的变形逐渐变为黏弹性变形，塑性应变逐渐减少，弹性应变逐渐增多．动弹性模量由10.5MPa衰减至8.7MPa，降低了17%，说明土体抵抗弹性变形的能力减小，进一步验证了随着振动阶段的增加，土体变形逐渐变为黏弹性变形的结论．

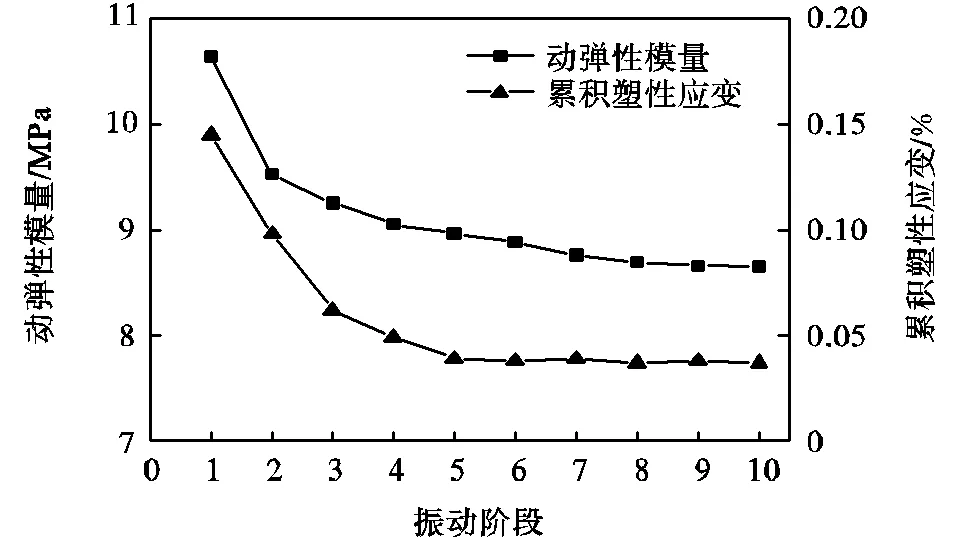
图4 各阶段的动弹性模量和累积塑性应变

2.2 累积塑性应变发展

为对比各阶段产生的累积塑性应变增量，将每一阶段的起始应变值归零，图5是3种不同频率下0＝1、d＝26kPa时分阶段加载的累积塑性应变发展曲线．由图5可知各阶段的累积塑性应变p在振动期逐渐增长，且增长速率逐渐减小，随着循环振动次数的增加，每一阶段引起的累积塑性应变逐渐减小，下一阶段产生的累积塑性应变峰值均小于上一阶段，在第6阶段即加载大约10000次后，各个阶段的累积塑性应变峰值逐渐趋于平稳．这与王军等[16]在交通荷载下得到的规律是类似的．对比3种不同频率条件下的累积塑性应变，可以发现频率越高，塑性变形相对较小，这说明地铁列车荷载频率对于土体累积塑性应变特性产生显著影响．

为与连续加载试验结果进行对比，在3种频率下0＝1、d＝26kPa时连续加载的累积塑性应变发展曲线如图6所示．从图6中可看出，轴向累积塑性应变随振动次数的增加而增大，并最终趋于稳定．另外，频率越高，塑性变形越小，这与分阶段加载的结果一致．但是分阶段加载试验中停振期累积塑性应变并非保持不变，而是在振动期结束的基础上逐渐减小到一个相对稳定值，即停振期存在部分应变恢复的现象.定义停振期应变恢复百分比为振动末期与停振末期应变值之差与振动末期应变值的相对百分比，图7为不同频率下各阶段停振期应变恢复百分比，可以看出，相对较高频率下，应变恢复的百分比相对较大，频率为1.5Hz时，第1阶段停振期恢复的最少，大约为20%，之后各阶段呈现逐渐增大的趋势，在第5阶段达到最大值27%．停振期可以使土体的黏弹性变形部分恢复或充分恢复，并且对后续阶段的振动产生影响，因此停振期对土体动力特性的影响是非常重要的.

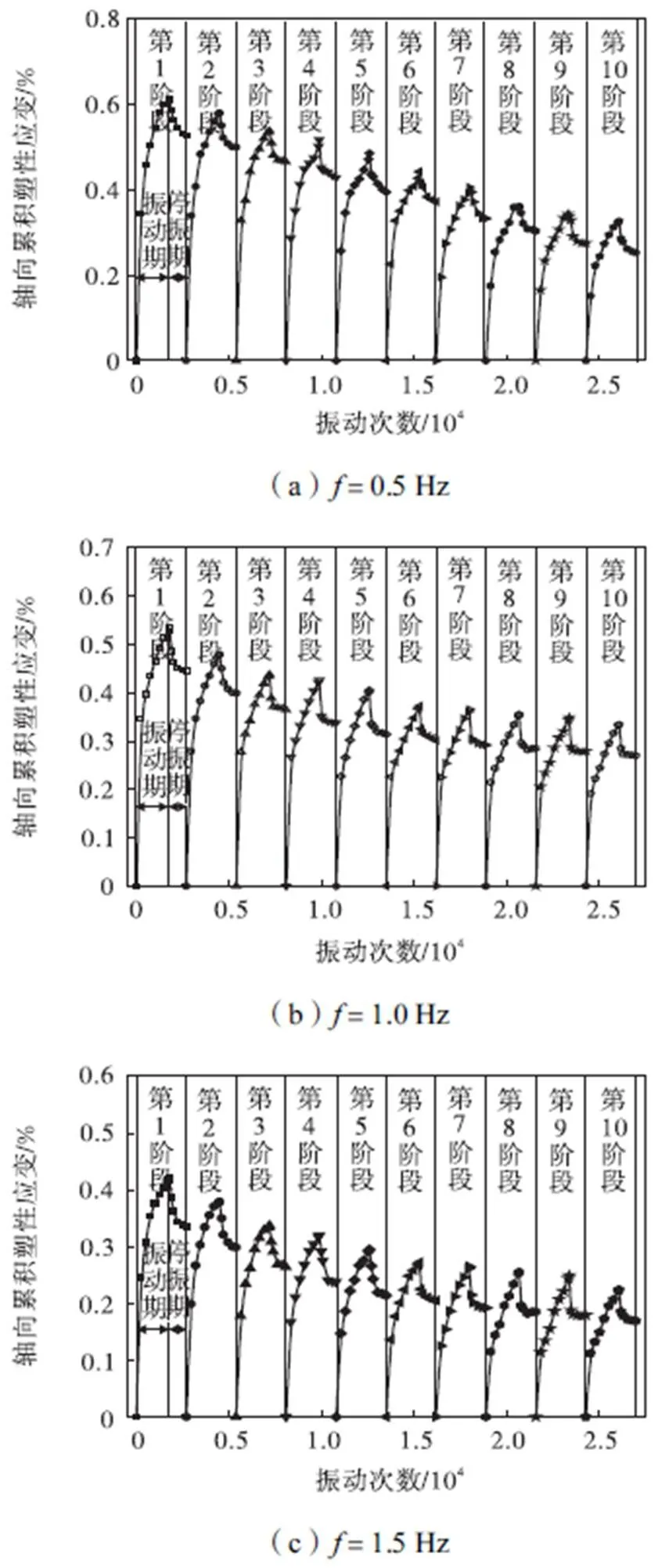
图5 不同频率下各阶段累积塑性应变发展曲线

图6 连续加载下累积塑性应变发展曲线

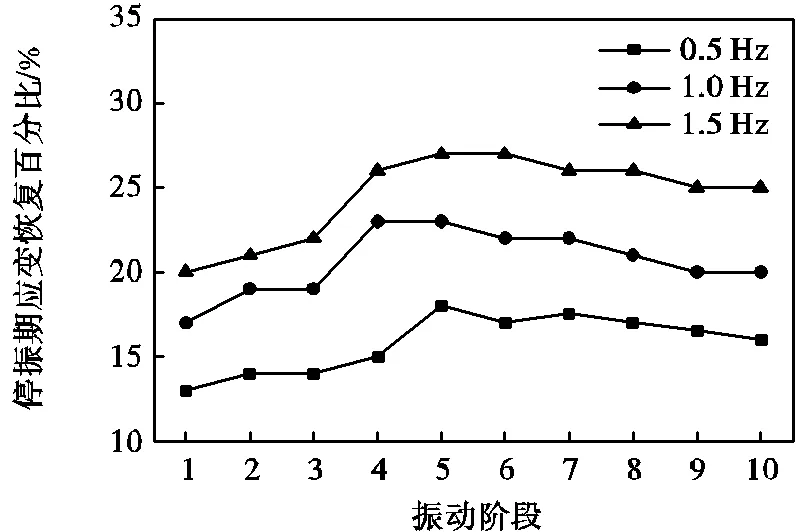
图7 不同频率下各阶段停振期应变恢复百分比

图8为不同频率下各阶段残余应变值，可知，频率越大，残余应变值越小，频率为0.5Hz时的残余应变值稍大于频率为1.0Hz和1.5Hz情况下的残余应变值．0.5Hz下第1阶段的振动期和停振期结束时的残余应变值分别为0.634%和0.525%，对应的1.5Hz下的残余应变值分别为0.421%和0.335%，说明随着振动频率的增加，塑性变形相应减少．另外，从图8中还可以看出，3种频率情况下随着振动阶段数的增加，各阶段的残余应变值不断减小直至趋于稳定，说明随着振动阶段的增加，土体逐渐被压密为黏弹性，导致塑性变形越来越少．

图8 不同频率下各阶段残余应变值

为研究不同固结形式和动应力比对轴向塑性累积应变的影响，选取频率＝1.5Hz时的试样S12～S15进行分析，其与振动次数的关系曲线如图9所示，从图9中可看出等压固结条件下的轴向塑性累积应变明显比偏压固结下的轴向塑性累积应变更大，土样处于等压固结状态时，受力均匀，土体更易被压密，累积应变就越大，说明固结形式对轴向塑性累积应变有显著的影响．另外，同一固结条件下，轴向塑性累积应变随动应力比增大而增大．动应力比为动应力幅值与有效固结围压之比，围压相同时，动应力幅值越大，对土体作用强度越强，累积应变就会越大．

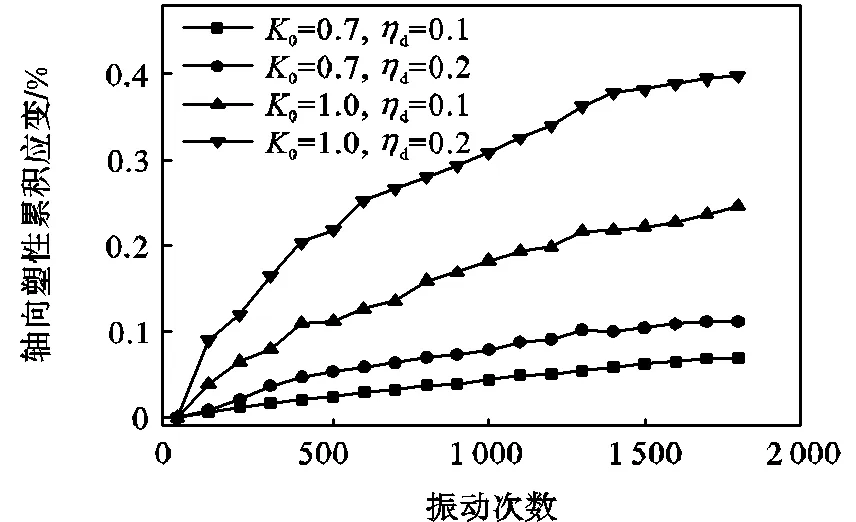
图9 不同固结条件和动应力比下轴向塑性累积应变与振次的关系曲线

2.3 累积孔隙水压力发展

图10为不同频率条件下S5、S10和S15试样各阶段累积孔隙水压力随振次发展曲线，为便于分析，将每一阶段的起始孔压值归零，分析该阶段的孔压增量值，即各阶段的累积孔隙水压力情况．从图10中可以看出，在循环动应力幅值相同时，随着振动阶段的增加，孔隙水压力的增量都是逐渐减小的，说明随着振动阶段的增加，每个阶段内振动期产生的累积残余孔压逐渐减小．

在停振期，孔压并不是稳定在振动末期累积孔压值附近[16]，而是在前5个振动阶段的停振期，孔压出现略微的增加，在第5个振动阶段之后，停振期的孔压开始下降，并在之后振动阶段的停振期中均呈现下降趋势．停振期由于试样不排水，振动期产生的动孔压无法消散，稳定在振动期产生的累积孔压值附近．与应变不同，停振期孔压发展并非全部减小，Zheng等[17]研究中揭示了停振期孔压值先上升后下降的情况．停振期孔压下降的原因可能如下：由于变形的滞后性，停振初期产生了部分累积塑性应变的恢复，造成了孔压的瞬时下降；同时孔压变化相应于应力和变形同样存在滞后效应，在不排水的条件下，随着振动次数的增加，软土压缩表现为黏弹性，此时循环动载引起的部分孔隙压力在振动周期结束时不能及时恢复，而在停振期软土有时间调整其内部结构，使弹性孔隙压力可以缓慢恢复．

对比图10(a)、(b)和(c)可以看出，频率越高，在振动期产生的动孔压越大，频率为0.5Hz时，振动阶段的最大累积动孔压在3kPa左右，而频率为1.5Hz时，振动阶段的最大累积动孔压在5kPa左右．由于饱和土体的变形受有效应力控制，因此频率越高时，所积累的动孔压越大，而有效应力越小，产生的变形也越小，这与应变发展的规律是相符的．

图10 不同频率下各阶段累积孔隙水压力发展曲线

3 结 论

本文针对天津地区饱和黏土，开展了一系列间歇性循环荷载条件下的循环三轴试验，分析了频率、不同固结条件和动应力比等因素对黏土动应力-动应变关系、累积塑性变形和动孔隙水压力发展规律的影响，其主要结论如下.

(1) 随循环阶段的增加，黏土的动应力-动应变滞回曲线逐渐向应变轴靠拢，且形状由“宽胖”渐变为“瘦削”，动弹性模量和平均残余应变随振次增加逐渐减小，且最终趋于一个稳定值．

(2) 饱和黏土的塑性累积应变随循环振次的增加而增大，停振期塑性累积应变并非保持不变，而是存在部分应变恢复现象，且频率越高，应变恢复越大；其应变恢复的原因为黏土的应变滞后效应；停振期对土体动力特性的影响是非常重要的．等压固结条件下的塑性累积应变明显比偏压固结下的累积应变更大，固结形式对轴向塑性应变有显著影响；塑性应变随动应力比增大而增大．

(3) 动孔压随着加载阶段的增加逐渐累积，在停振期，动孔压在振动前期阶段增加，而在振动后期阶段出现了下降的现象，其可能的原因为黏土的应变滞后产生的变形恢复造成了孔压的下降；频率越高，在振动期产生的动孔压越大．

［1］ 潘昌实，谢正光. 地铁区间隧道列车振动测试与分析[J]. 土木工程学报，1990，23(2)：21-28.

Pan Changshi，Xie Zhengguang. Vibration test and analysis of subway tunnels[J]. China Civil Engineering Journal，1990，23(2)：21-28(in Chinese).

［2］ 曹新文，蔡 英. 铁路路基动态特性的模型试验研究[J]. 西南交通大学学报，1996，31(1)：36-41.

Cao Xinwen，Cai Ying. Model test study on dynamic characteristics of railway subgrade[J]. Journal of South- west Jiaotong University，1996，31(1)：36-41(in Chinese).

［3］ 唐益群，赵 化，王元东，等. 地铁荷载下隧道周围加固软黏土应变累积特性[J]. 同济大学学报：自然版，2011，39(7)：972-977.

Tang Yiqun，Zhao Hua，Wang Yuandong，et al. Characteristics of strain accumulation of reinforced soft clay around tunnel under subway vibration loading[J]. Journal of Tongji University：Nature Science，2011，39(7)：972-977(in Chinese).

［4］ 叶耀东，朱合华，王如路. 软土地铁运营隧道病害现状及成因分析[J]. 地下空间与工程学报，2007(1)：157-160，166.

Ye Yaodong，Zhu Hehua，Wang Rulu. The present situation and cause analysis of tunnel diseases in soft soil iron operation[J]. Chinese Journal of Underground Space and Engineering，2007(1)：157-160，166(in Chinese).

［5］ 陈德智. 广州地铁道运营期沉降监测及分析[J]. 都市快轨交通，2011，24(4)：94-98.

Chen Dezhi. Monitoring and analysis of subsidence during Guangzhou metro operation period[J]. Urban Rapid Rail Transit，2011，24(4)：94-98(in Chinese).

［6］ Andersen K H，Pool J H，Brown S F. Cyclic and static laboratory tests on Grammen clay[J]. Journal of Geotechnical Engineering Division，ASCE，1980，106 (GT5)：499-529.

［7］ Yasuhara K，Hirao K，Hyde A F L. Effects of cyclic loading on undrained strength and compressibility of clay[J]. Soils and Foundations，1992，32(1)：100-116.

［8］ Moses G G，Rao S N，Rao P N. Undrained strength behavior of a cemented marine clay under monotonic and cyclic loading[J]. Ocean Engineering，2003，30(14)：1765-1789.

［9］ 唐益群，黄 雨，叶为民，等. 地铁列车荷载作用下隧道周围土体的临界动应力比和动应变分析[J]. 岩石力学与工程学报，2003，22(9)：1566-1570.

Tang Yiqun，Huamg Yu，Ye Weimin，et al. Critical dynamic stress ratio and dynamic strain analysis of soils around the tunnel under subway train loading[J]. Chinese Journal of Rock Mechanics and Engineering，2003，22(9)：1566-1570(in Chinese).

［10］ 黄茂松，李进军，李兴照. 饱和软黏土的不排水循环累积变形特性[J]. 岩土工程学报，2006，28(7)：891-895.

Huang Maosong，Li Jinjun，Li Xingzhao. Cumulative deformation behavior of soft clay in cyclic undrained tests [J]. Chinese Journal of Geotechnical Engineering，2006，28(7)：891-895(in Chinese).

［11］ 雷华阳，姜 岩，陆培毅，等. 交通荷载作用下结构性软土动应力-动应变关系试验研究[J]. 岩石力学与工程学报，2008，27(增1)：3052-3057.

Lei Huayang，Jiang Yan，Lu Peiyi，et al. Experimental study on dynamic stress-dynamic strain relationship of structural soft soil under traffic load[J]. Chinese Journal of Rock Mechanics and Engineering，2008，27(Suppl 1)：3052-3057(in Chinese).

［12］ 郑 刚，霍海峰，雷华阳，等. 振动频率对饱和黏土动力特性的影响[J]. 天津大学学报：自然科学与工程技术版，2013，46(1)：37-43.

Zheng Gang，Huo Haifeng，Lei Huayang，et al. Contrastive study on the dynamic characteristics of saturated claying different vibration frequencies[J]. Journal of Tianjin University：Science and Technology，2013，46(1)：37-43(in Chinese).

［13］ 王常晶，陈云敏. 列车荷载在地基中引起的应力响应分析[J]. 岩石力学与工程学报，2005，24(7)：1178-1186.

Wang Changjing，Chen Yunmin. Analysis of stresses in train-induced ground[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(7)：1178-1186(in Chinese).

［14］ 杨兵明，刘保国. 地铁列车循环荷载下软土地区盾构隧道长期沉降分析[J]. 中国铁道科学，2016，37(3)：61-67.

Yang Bingming，Liu Baoguo. Analysis of long-term settlement of shield tunnel in soft soil area under cyclic loading of subway train[J]. China Railway Science，2016，37(3)：61-67(in Chinese).

［15］ 丁 智，张 涛，魏新江. 地铁列车循环荷载试验论证研究[J]. 地震工程学报，2015，37(3)：789-793.

Ding Zhi，Zhang Tao，Wei Xinjiang. Experimental study on the cyclic loading of metro trains[J]. China Earthquake Engineering Journal，2015，37(3)：789-793(in Chinese).

［16］ 王 军，蔡袁强，郭 林，等. 分阶段循环加载条件下温州饱和软黏土孔压和应变发展规律[J]. 岩土工程学报，2012，34(7)：1349-1354.

Wang Jun，Cai Yuanqiang，Guo Lin，et al. The regularity of pore pressure and strain development of Wenzhou saturated soft clay under cyclic loading by stages[J]. Chinese Journal of Geotechnical Engineering，2012，34(7)：1349-1354(in Chinese).

［17］ Zheng Qingqing，Xia Tangdai，Ding Zhi，et al. The effect of periodic intermittency on the cyclic behavior of marine sedimentary clay[J]. Marine Georesources & Geotechnology，2019，37(8)：945-959.

Experiment of Dynamic Characteristics of Saturated Remolded Clay Under Intermittent Cyclic Loading

Lei Huayang1, 2, 3，Yang Xiaonan1，Xu Yinggang1，Zhang Lei1

(1. School of Civil Engineering，Tianjin University，Tianjin 300350，China；2. Binhai Key Laboratory of Civil Engineering Structure and Safety，Ministry of Education，Tianjin 300350，China；3. Key Laboratory of Earthquake Engineering Simulation and Seismic Resilience，CEA，Tianjin 300350，China)

Aiming at the long-term settlement of foundation caused by subway train load during operation period，the influence of the confining pressure and consolidation ratio on the long-term dynamic characteristics of soil has been considered in previous triaxial tests. However，the characteristics of periodicity and intermittence are ignored in the simulation of the subway train load. Based on this，a series of cyclic triaxial undrained tests under intermittent cyclic loading are conducted in this study for the saturated clay in Tianjin area. Influences of the intermittent period and frequency of vibration load on the cumulative plastic strain，dynamic stress-strain relationship，and pore pressure development of the clay are analyzed. The effect of the different consolidation ratios and dynamic stress ratios on the axial plastic cumulative strain is also discussed. Results show that with increased vibration stage，the hysteretic shape of the dynamic stress-strain curve of the saturated clay gradually develops to the strain axis，the cumulative plastic strain of clay increases，and the growth rate gradually decreases. Due to the hysteresis effect of soil mass，some accumulated plastic strain is restored in the static period. With increased vibration times，the residual strain decreases to a stable value. The axial plastic cumulative strain under constant compression consolidation is obviously larger than that under bias consolidation condition. Under the same consolidation condition，the axial plastic cumulative strain increases with the increased dynamic stress ratio. The accumulated dynamic pore pressure gradually accumulates with the vibration stage，while it increases slightly in the stopped vibration stage of the vibration cycle stage. In the latter part of the vibration stage，the phenomenon of decline occurs in the vibration stopping period due to the viscoelastic behavior of soil compaction.

remolded clay；intermittent cyclic loading；hysteresis effect；dynamic characteristic

TU471

A

0493-2137(2021)08-0799-08

10.11784/tdxbz202007041

2020-07-15；

2020-10-16.

雷华阳（1974—  ），女，博士，教授.

雷华阳，leihuayang74@163.com.

国家重点研发计划资助项目(2017YFC0805407)；国家自然科学基金资助项目(51578371)；土木工程防灾国家重点实验室开放课题基金资助项目(SLDRCE17-01)。

Supported by the National Key Research and Development Program of China(No. 2017YFC0805407)，the National Natural Science Foundation of China(No. 51578371)，the Open Project of State Key Laboratory of Disaster Reduction in Civil Engineering (No. SLDRCE17-01).

(责任编辑：金顺爱)