基于VAR 模型河南省城镇化发展与经济增长关系的实证研究

2021-04-25常文超

市场周刊 2021年4期

常文超

(郑州工业应用技术学院，河南新郑451100)

一、研究背景

人类历史社会发展就是城镇化的发展，纵观世界各国，美国、英国、日本和韩国等发达国家早在2011 年城镇化率已经处于很高的比率，分别为82.40%、79.62%、91.27% 和83.22%，这代表了这些国家的城镇化水平很高，而截至目前，中国的城镇化率也才未超过60%。可见，我国城镇化水平仍与发达国家存在一定差距，为了追上发达国家经济水平，全面实现社会主义现代化，从而更好地推进农村农业农民问题解决，走中国特色的新型城镇化道路是必然的选择。河南省政府一直把加快城镇化建设与提高城镇化水平作为全省发展的重点，在现有的条件下河南省城镇化发展面临哪些难题，它与区域经济发展又产生怎样的关联，如何保证持续健康的发展，如何推动城镇化快速的进步，都是值得思考的问题。故论文以研究新型城镇化与经济增长的实证关系为出发点，探索新型城镇化的发展道路，并给出一些发展建议。

二、模型介绍及变量选择

(一)VAR 模型

向量自回归模型，即VAR 模型，是针对多个变量，以平稳变量为前提，分析不同变量之间数量关系的计量经济学模型，是在单变量自回归模型的基础上向多变量的推广。具体指在没有任何前提约束的条件下，用来描述估计时间序列变量与其所有内生变量滞后值之间存在的关联。如果多个变量与其滞后值之间存在关系，我们可以用线性函数来实现，比如p阶向量自回归模型记作VAR(p)，它的函数可以写成：

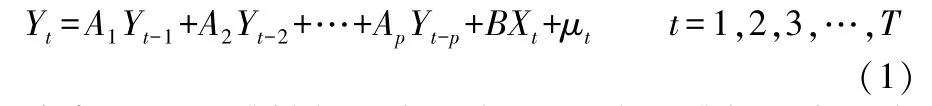
式中，Yt是k维被解释变量向量；Xt为d维解释变量向量；μt是k维随机误差向量；p为滞后阶数，A1，A2，…，Ap和B是待估系数，样本个数为T。

(二)变量及数据选取

研究选取河南省城镇化率(记作CR)即城镇人口占总人口的比率作为新型城镇化变量，河南省人口数量多，且基数变化快，所以为了剔除数量和价格因素的影响，论文选用平均指标作为经济水平的代表，即人均GDP(记作PGDP)，那经济增长就代表是人均GDP 的增加额。数据收集主要通过中国和河南省统计局网站，查看《中国统计年鉴》和《河南统计年鉴》，样本选取1995～2017 年的河南省城镇化率和人均GDP 的变量时间序列数据，通过对数化处理并分别记作lnCR 和lnPGDP，为了使结果更加科学化，需要消除异方差的影响，同时排除价格和数据本身的波动性，通过测度这两个变量指标以及其滞后值之间的关系来说明两者之间的动态关系，数据的处理和结果的获取均通过计量软件EViews8.0来完成。

三、新型城镇化发展与经济增长关系实证分析过程

(一)ADF 单位根检验

VAR 模型是针对平稳时间序列多元变量建立的，若变量是平稳的可直接建立，若变量是不平稳的，要进行Johansen协整检验，否则很可能形成伪回归，那研究变量之间的动态关系就没有意义。故对lnCR 和lnPGDP 进行单位根检验，若结果是非平稳的，需要进行差分处理，检验的结果主要通过比较T 检验值和在不同显著性下的临界值来确定，若T 检验值大于临界值，则接受原假设，说明序列存在单位根，即两变量的时间序列是平稳的；若T 检验值小于临界值，则拒绝原假设，说明序列不存在单位根。根据对1995～2017 年的lnCR和lnPGDP 进行单位根检验，有(Ⅰ)有截距、(Ⅱ)有趋势、(Ⅲ)没有截距三种情形，三种情形下检验结果根据AIC、SC信息准则比较它们的AIC、SC、HQ 值，最小值最多的即为所要结论。按照这个原理，经EViews8.0ADF检验操作得知，均不拒绝原假设，也就是这两个变量时间序列均为不平稳的。所以只能差分处理检验。经过二阶差分后T 检验统计值均小于临界值，故拒绝原假设，即二阶差分后两者时间序列均为平稳时间序列，二阶差分后的lnCR 和lnPGDP 结果参看表1。

从表1 各变量差分后单位根检验结果可知lnPGDP 时间序列的T 检验值-2.7093 均大于显著性分别为1%、5%、10%的临界值-4.5326、-3.6736 和-3.2774，和lnCR 时间序列的T检验值-2.7241 大于-4.4441、-3.6329 和-3.2547，故不拒绝该假设，时间序列不平稳。一阶差分后，依旧不平稳。二阶差分后，lnPGDP 时间序列的T 检验值-4.9023 和lnCR 时间序列的T 检验值-5.8323 均小于显著性为1%、5%、10%对应的临界值，故拒绝原假设，也就是说经过二阶差分处理后，ln-PGDP 和lnCR 记作I(2)，是二阶单整平稳序列，符合建模要求。

(二)最优滞后阶数的确定

一般情况下，两个内生变量lnCR 和lnPGDP 因果关系不会同时发生，会有时间滞后，在一段时间后才会对被解释变量产生影响。在进行Johansen 协整检验前要先确定VAR 模型的滞后阶数，从而选择一个最佳滞后期。 VAR 模型滞后期选择可以通过LR(似然比)检验和信息准则判断，根据5 个指标值显示结果，带∗号值(即对应指标最小值)最多的阶数就是我们要的最优阶数。根据EViews8.0 操作，得到滞后期阶数选择标准表，如表2 所示。根据表2 VAR 滞后期选择的5 个指标显示，本研究应该建立VAR(3)模型进行分析，即最优滞后阶数为3。

表2 VAR 模型最优滞后期选择标准

(三)Johansen 协整检验

Johansen 协整检验是针对不平稳时间序列为建立VAR模型进行的检验，可判断多元变量间是否存在长期均衡关系，从而解释变量间存在的关系，不能通过Johansen 协整检验就是伪回归。我们一般说lnCR 和lnPGDP 变量具有协整性，即两者之间存在长期均衡关系，主要看这两个变量能否组合成一个平稳序列，若可以，这两个变量之间就存在协整关系。 Johansen 协整检验需要进行多次连续检验，在检验前先提出原假设H0：有0 个协整关系，即没有协整关系；H1：至多有1 个协整关系；经检验发现选择序列有截距项且变量间有线性趋势，协整检验的滞后区间比VAR 的滞后阶数小1，因VAR 的最优滞后阶数是3，故协整检验的滞后区间为“12”，根据EViews8.0 操作，结果如表3 和表4 所示。

表3 Johansen 协整检验结果

表4 Johansen 协整检验结果

通过协整检验结果可知，对于原假设“至多1 个协整关系”，“特征根迹检验”9.999512 和“最大特征值检验”，小于在显著性水平为5%的情况下的临界值12.51798，故接受原假设，即存在至多1 个协整关系；对于原假设“没有协整关系”，“特征根迹检验” 27.13381 和“最大特征值检验”19.38704，均大于在显著性水平为5% 的情况下的临界值25.87211和17.13430，故拒绝原假设即有协整关系；因此，ln-PGDP 和lnCR 变量之间具有长期均衡关系，根据表5 得出这两个变量之间的长期协整方程：

表5 VAR 标准协整向量系数

协整方程结果显示，新型城镇化率水平每提高1%将促进经济增长5.0219%，即两者之间存在长期均衡关系，从方程可以看出即河南省新型城镇化与经济增长之间具有正向的协整关系。

VAR 模型稳定性检验可以通过判定其特征根值是否落到单位圆内来判定，EViews8.0 软件操作得知结果如图1 所示，均落到了单位圆内，并且VAR(3)模值均小于1(表6)，故模型是稳定的，即协整方程也是稳定的，这为后续脉冲相应的分析提供了前提条件。

图1 VAR(3)稳定性检验结果

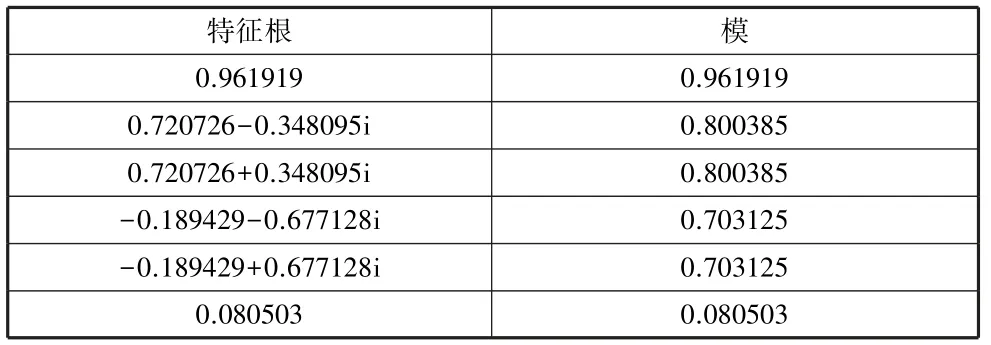
表6 VAR(3)稳定性检验特征根的模值

(四)格兰杰因果检验

VAR 模型只能基于软件回归分析得两个变量之间存在依存性关系，但是不能清楚说明两个变量之间关系是因果关系及其方向，即两个变量间谁先谁后。格兰杰因果检验可以对两个平稳的时间序列变量考虑了其滞后值的情况下一个变量变化是否引起另一个变量变化，若是，就说此变量为另一个变量的格兰杰原因，当然，这个因果关系是统计意义数据关系上，不代表实际现实活动关系。故对平稳的时间序列变量lnCR 和lnPGDP 进行格兰杰因果检验，来分析两者之间因果关系的先后问题。一般的格兰杰检验结果有四种：①lnCR 是lnPGDP 的格兰杰原因，即存在lnCR 到lnPGDP 的单向因果关系；②lnPGDP 是lnCR 的格兰杰原因，即存在ln-PGDP 到lnCR 的单向因果关系；③lnPGDP 和lnCR 互为格兰杰原因，即具有双向因果关系；④lnPGDP 和lnCR 是独立的，或lnPGDP 和lnCR 间不存在因果关系。我们选择F 检验，通过判断在显著水平为5%的情况下，F 统计量的P值是否小于5%，若小于，则拒绝原假设，若大于，则接受。

前面我们已经证明了lnPGDP 和lnCR 之间存在着协整关系，选择滞后阶数为3，进行格兰杰因果检验，结果如表7所示。

表7 格兰杰因果关系检验结果

从上述检验结果可以看出，在显著性水平为5%的情况下，lnPGDP 不是lnCR 的格兰杰原因的P值为0.3161，大于0.05，故接受原假设，也就是说河南省经济增长不是新型城镇化的格兰杰原因；lnCR 不是lnPGDP 的格兰杰原因的P值为0.0041 小于0.05，故拒绝原假设，也就是说，新型城镇化是经济增长的格兰杰原因，两者存在单向的格兰杰因果关系。综上所述，新型城镇化水平的变化可以带来经济增长，但经济增长不会直接带来新型城镇化水平变化，从经济现象上理解，新型城镇化通过人口转移，城镇化的过程中改变了消费观念，扩大了内需，从而带动了经济的增长，经济增长更多是一种本身的长期的趋势的驱动，与城镇化的关联不大，也就是说即使排除城镇化影响，经济也保持一定的增长趋势。

(五)脉冲响应分析

VAR 是一个系统，单独的方程只能解释局部关系，不能满足复杂的系统关系，所以我们就可以通过脉冲响应分析和方差分解来看系统内变量扰动项对所有变量当前值和未来趋势变化的贡献。为了进一步讨论lnPGDP 扰动项和lnCR扰动项在VAR 模型中的动态关系，利用EViews8.0 软件，我们得到在一个标准差冲击下河南省人均GDP 和城镇化率的脉冲响应图，如图2 和图3 所示：

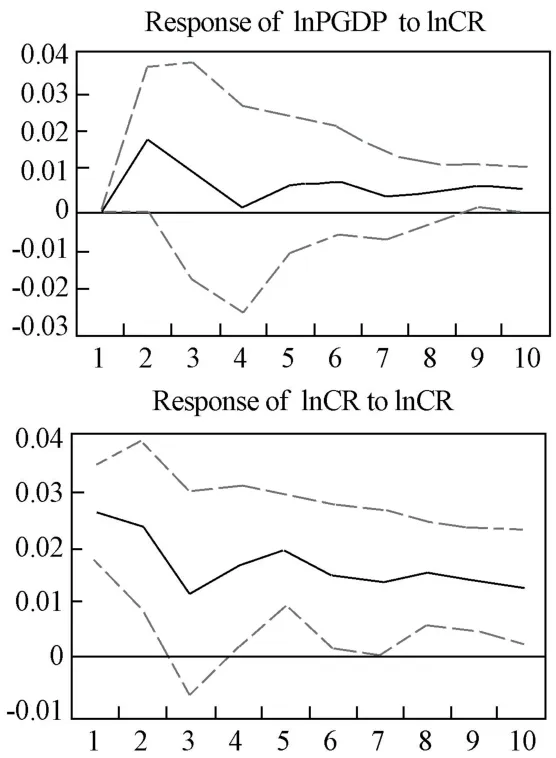
图2 lnCR 对lnGDP 的脉冲响应

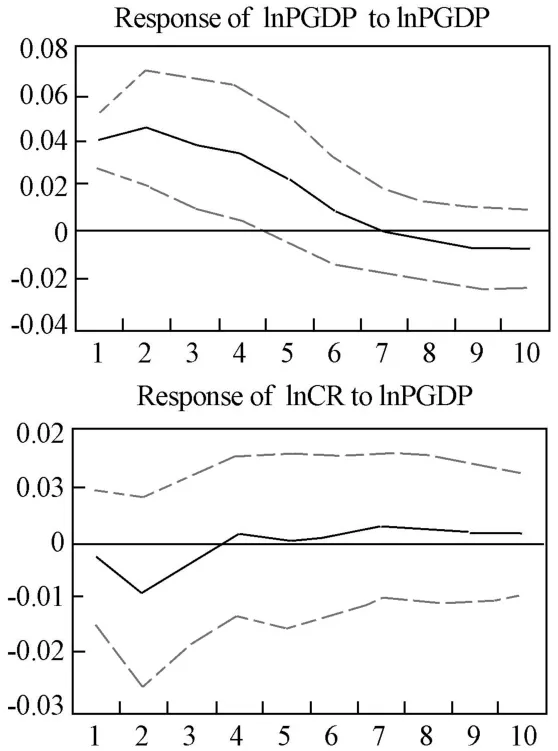
图3 lnGDP 对lnCR 的脉冲响应

从图2 可以看出，城镇化率扰动项对经济增长的冲击效果在第1 期到第2 期略微增长为2，第2 期到第4 期下降达到接近0，随后又有轻微的增大的趋势，但都在0 附近，即趋于平稳。这说明，以城镇化率水平代表的城镇化发展长期以来对经济增长的影响一直是正向的，开始是增大，随后降低，最后趋于平稳；城镇化率扰动项对自身的正向冲击第1 期到第3 期由2.7 下降到1，第3 期到第5 期略微上升，第5 期之后开始下降并趋近于0。

从图3 可以看出，经济增长的扰动项对城镇化率的冲击效果第1 期到第2 期负向有所增加，第2 期后有上升趋势并逐渐趋近于0，第4 期之后，基本趋于平稳。这说明，以人均GDP 为代表的经济增长对城镇化发展的影响一开始是先略微负向波动，后从第4 期接近零基本保持平稳，且为积极的正向的响应。人均GDP 对自身的冲击从第1 期到第7 期由2.8 逐渐下降为0，且为正向，第7 期后负向略微增大又回归0附近，逐渐趋于平稳。

综上所述，河南省城镇化的发展对经济增长的作用一直是正向的，这与格兰杰检验的结果相一致，经济增长对河南城镇化发展短期内的影响是负向的，随后开始出现轻微的正向影响，且有上升趋势，主要是因为早期的城镇化一直是粗放的土地城镇化，可能对其造成一些负面的影响，后期新型城镇化强调可持续性，逐渐的产生一些积极正向的影响。

(六)方差分解

方差分解就是指在系统内内生变量受所有变量变化的影响比率，一般用百分比表示，意思是某一个变量的变化是由自身和另外一个变量分别贡献的百分比。通过方差分解研究河南省新型城镇化发展由其自身所带来的变化和经济增长的变化的贡献度，利用EViews8.0 对lnCR 的方差分解，得到图4 和表8。

图4 lnCR 的方差分解图

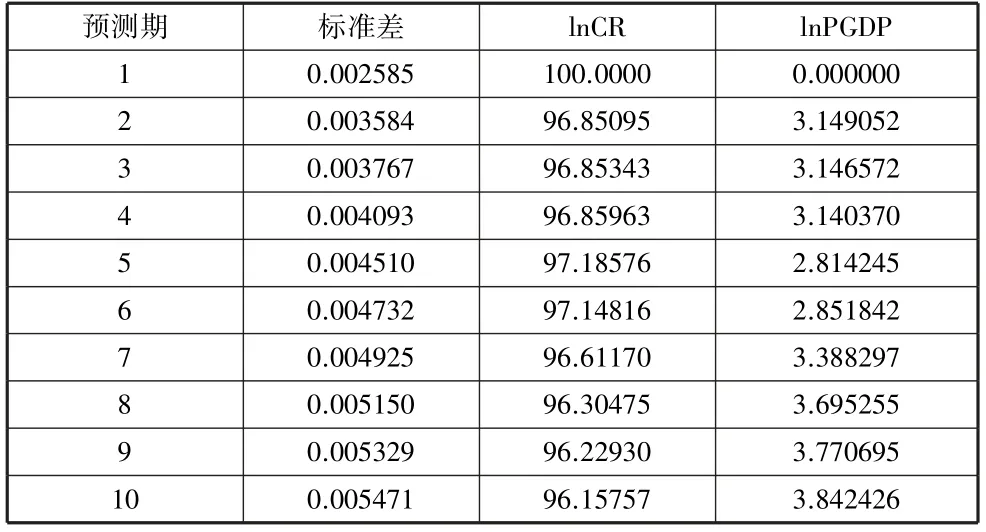
表8 lnCR 的方差分解表

从表8 可以看出，在第一期，城镇化率变化100%是自身作用，从第二期人均才逐渐显现，占比3%左右，第5 期有所下降，第7 期有所回升且逐步扩大，但最终都控制在4%以内的贡献度，也就说明河南省城镇化发展变化主要还是由于自身影响的程度大，与经济发展并没有太大的关联，可能是因为经济增长并没有有力扶持城镇化水平的提升，在以后的发展过程中，可加大对此的投入和重视程度。

从图5 和表9 中可以看出，河南省经济增长的变化由其自身的影响程度要大于城镇化率水平的提高，第1 期人均GDP 的贡献率占比接近99%，说明自身的发展趋势带来的影响更大，从第2 期之后，有所回落，到第10 期下降到91%，而城镇化率从第1 期0.82%逐步上升，第10 期达到9%，说明城镇化的发展对经济增长趋势影响将逐步增大，也印证了我们原来的结论，就是河南省城镇化发展能够正向促进经济增长，且影响的比重越来越大。