电动力学课程教学中对带电粒子自旋极化度的分析理解

温 猛，陈紫晗

（湖北大学 物理与电子科学学院，武汉 430062）

0 引言

电动力学是研究电磁现象的经典动力学理论，它主要研究电磁场的基本属性、运动规律以及电磁场和带电物质的相互作用。电动力学课程是物理学专业和应用物理学专业的本科核心理论课程。然而在教学过程中，存在理论性强、抽象内容多、公式推导烦琐等特点，如只注重理论知识讲授很难激起学生的学习兴趣，使学生保持长期的专注度。

近年来，强激光技术发展迅速，带电粒子束的自旋特性引起广泛的研究兴趣。自旋是量子力学引入的由粒子内禀角动量引起的内禀运动。在量子力学中，自旋是用自旋算符进行描述的。对刚接触量子力学的学生来说，算符和自旋都是非常抽象的概念，难以理解，难以和物理模型对应起来。实际上，带电粒子在电磁场中的运动是电动力学课堂教学的重点内容，运动规律遵循洛伦兹公式。在经典电动力学中，粒子的自旋角动量用单位矢量表示。经典的自旋矢量及其相对应的自旋极化度的描述方法，对学生来说，更容易理解和接受。利用电动力学的经典模型，我们可以方便地研究带电粒子的自旋极化度在平面电磁波中的演化过程，通过这个实例，使得学生对自旋有一定的认识，为量子力学的学习做一个过渡；依托基础理论教学与前沿研究、科研实践相融合的模式，使得学生对物理学前沿研究有一定的了解，可以加深学生对电动力学基础知识的理解和掌握，激发学生的学习兴趣和研究热情。

中学和大学的物理课程中已经介绍了电荷和电磁场的耦合使得电荷受到洛伦兹力而运动。类似的，磁矩和电磁场耦合的结果是磁矩在电磁场中的转动。这种现象用粒子的自旋演化描述，称为自旋量的进动。实际应用中，很多粒子除了携带动量信息，还会携带自旋角动量信息。比如质子、中子、电子、中微子和夸克都是自旋1／2 粒子。在普通高校物理专业的课程设置中，自旋更多是在量子力学中引入。大部分学生第一次接触到的粒子自旋态是量子力学中的概念，是粒子的一个内禀的自由度，然而并没有一个形象化的物理过程与之对应。量子力学的学习过程中，波函数、算符、矩阵等抽象的描述方法等，都加大了学生理解物理概念上的难度。学生需要一个从经典到量子、从具象到抽象的过渡。实际上，在电动力学中，也可以用自旋矢量及其相对应的自旋极化度的方法进行描述。带电粒子的自旋作为一个交叉领域的概念在经典电动力学和量子力学中都有介绍，它们相通的地方是电动力学的自旋矢量对应于量子力学中自旋算符在某自旋态下的期望值。量子力学中，自旋1／2 粒子在态ψ=（a，b）T下的自旋由算符σh/2 表示，其中σ 为泡利矩阵。在经典电动力学中，归一化的粒子的自旋角动量用单位矢量s 表示，它对应于泡利算符在某自旋态下的平均值s=〈ψ|σ|ψ〉。本文基于这个自旋矢量讨论带电粒子自旋极化度的概念，其物理意义为粒子自旋在方向n 上自旋向上和自旋向下的概率差，用于描述单粒子或粒子束的自旋极化度。它可以用量子力学中自旋算符此方向的期望值计算，根据本文介绍，也可以用P=s·n 计算。例如，在直角坐标的z 方向计算的自旋极化度为s·ez=〈ψ|σz|ψ〉=a2-b2。

1 基础理论知识

本文以电子为例讨论粒子的自旋极化问题。带电粒子的电量、质量和动量分别用q、m 和p=γmcβ 表示，这里β=v/c 为归一化的粒子速度，为洛伦兹因子，c 为真空中的光速。首先，带电粒子在电磁场中的运动方程由洛伦兹公式给出：

同时，其自旋矢量s 在电磁场中的进动方程可以写为：

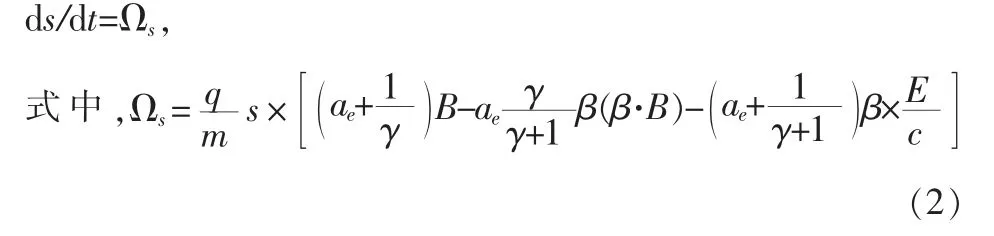
这里ae=0.00 116，为电子的异常磁矩。

本文讨论粒子在运动方向n=β/|β|的纵向自旋极化度P=s·n，这个物理量也被称为粒子的螺旋度。根据公式1 经过推导可以得到粒子运动方向的演化公式dn/dt=Ωv，其中

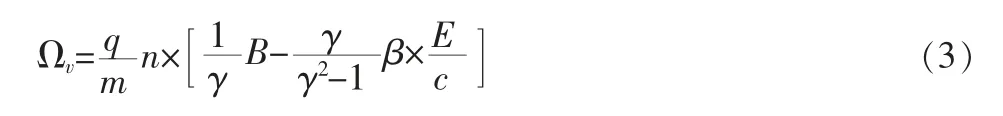
再进一步推导可得粒子自旋极化度随时间演化的规律

为了更直观地理解电磁场对带电粒子自旋极化度的影响，下面用数值的方法讨论带电粒子在平面电磁场中的动量和自旋极化度的演化情况。

2 带电粒子螺旋度在平面电磁场中的演化

通用的量子力学教程介绍过定域电子在均匀磁场中的进动频率，然而对于非定域电子的自旋进动的情况，用量子力学的方法计算是非常复杂的。本文用经典电动力学的方法，考虑一个初始动量为p0的带电粒子沿x 轴正向运动，一个脉冲型平面电磁波沿x 轴负向传播，带电粒子在电磁波中运动和自旋情动的情况。带电粒子初始是完全纵向极化的P0=s0·ex=100%，

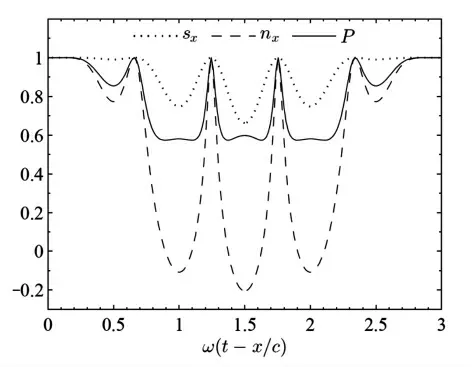
图1 初始动量为p0=0.2mc 的带电粒子在平面电磁场中自旋、运动方向、极化度随着相位的演化

电磁波在峰值ω（t-x/c）=T/2 附近对粒子的退极化能力是依赖于粒子自身的动量的，这一点可以从公式（2）～公式（4）看出。粒子的极化度变化率决定于粒子自旋和运动方向偏转速度的差Ωs-Ωv≈（q/m）（1/|β|-|β|）（n×E/C），由此可以知道粒子极化度变化率会随着粒子速度β 的增大而变小。所以，电磁波对初始动量较高的粒子的退极化会较弱。图2 的结果也印证了这个结论。图2 的横轴为粒子在电磁波中的相位，纵轴为粒子的初始动量，图中阴影的强度表示粒子的瞬时极化度。由此可以看出，在粒子的初始动量p0较小时，其极化度可以被退极化即sx0=1。平面电磁波的形式由Ey=2πmc2/（|q|λ）sin2［（t-x/c）T］sin［ω（t-x/c）］给出，其中λ 为电磁波的波长，T=3λ/c 为电磁波的脉冲宽度，ω（t-x/c）为带电粒子所在位置x 对应的电磁场的相位。由于粒子的速度一定小于真空中的光速c，随着时间的增长，相位值（ct-x）/λ 也会单调的增大。在电磁场的电场表达式中，2πmc2/（|q|λ）为电场的振幅，当λ=1μm 时，该电场振幅对应的电磁波能流强度为1.37×1018W/cm2。由于电磁波沿x 轴负向传播，其磁场可以表示为Bz=-Ey/c。

当一个初始动量为p0=0.2mc 的带电粒子穿过该电磁场时，该粒子的自旋矢量和运动方向均会在电磁场中发生偏转，偏转的角速率由公式（2）和公式（3）决定。它们在x 轴上的分量sx和nx=n·ex如图1 的点线和虚线所示，由此可以看出，粒子的相位越接近平面电磁场脉冲的峰值ω（t－x／c）＝T/2，它们的变化值越大。然而，点线和虚线的区别表示粒子的自旋矢量和运动方向偏转的角度不同，所以两矢量的内积，也就是该粒子的纵向自旋极化度P=s·n=sxnx+syny+sznz会在粒子穿过平面电磁场时发生变化。通过数值运算，可以看出粒子自旋极化度P 也在电磁波峰值附近发生较强的退极化，会从初始的100%极化降低到60%左右，如图1 中的实线所示。此外，还可以看出，由于脉冲型电磁波的震荡对称性，粒子穿过电磁波峰值之后，自旋s和运动方向n 都会逐渐回到初始的方向。也就是说，粒子穿过平面电磁波之后，电磁波不会对粒子的自旋、动量以及极化度产生净效果。到较小值，也就是阴影部分较暗；在初始动量p0较大时，粒子的极化度会保持在一个较高的范围，也就是阴影部分较亮。我们上面也用本文提供的理论知识解释了这个现象。

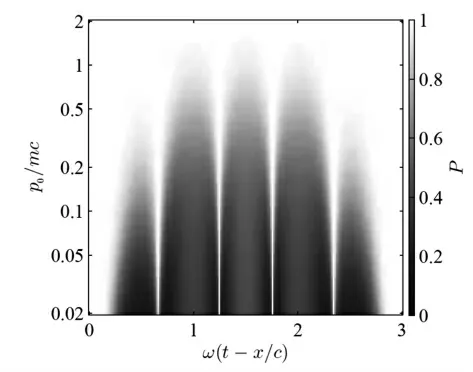
图2 初始动量为0.02mc～2mc 的带电粒子在平面电磁场中自旋、运动方向、极化度随着相位的演化

3 结语

本文用经典电动力学的概念，分析理解了带电粒子在电磁场中极化度变化的情况。这可以帮助本科物理专业高年级学生学习理解电动力学和量子力学课程中相近和相通的粒子自旋这个物理概念。虽然粒子极化度在电动力学和量子力学中都是一个比较基础的概念，但是它在粒子物理，高能物理领域都占据非常重要的地位，也存在很多难以解释和难以解决的自旋相关的现象和问题。本文介绍的这个简单的物理过程也是自旋动力学的一个关键环节。通过对本物理过程的理解和认识，为开阔学生视野，提高学生兴趣，加强本科学生对科学前沿研究的认识提供素材，并能有效增进课堂教学效果，提升整体教学质量。