浅谈思维导图在小学数学概念教学中的应用
2021-04-23于婷婷




【摘 要】数学概念具有高度的概括性和抽象性,是数学理论的基础。在小学数学概念教学中借助思维导图,进行高效的“教”与“学”,可以帮助学生了解概念的内涵与外延,梳理概念间的联系与区别,构建知识间的结构框架,发展学生的概括能力,发散学生的数学思维,提升其核心素养。
【关键词】小学数学;概念教学;思维导图
【中图分类号】G623.5 【文献标识码】A 【文章编号】1671-8437(2021)34-0163-03
思维导图又叫心智导图,是表达发散性思维的有效图形思维工具。思维导图运用图文并重的形式把各级主题的关系用相互隶属或层级的方式展示出来,能够帮助学习者建立更为直观和系统的知识体系。
小学数学概念是每一个单元或章节所学习的重点,也是后续学习的基础。据统计,在小学阶段需要学生掌握的数学概念大约有500多个,可以说概念教学是小学数学教学的重要组成部分。然而到了高年级后,经常会出现这样的现象:一些学生不能灵活解题,不能够举一反三,甚至有些学生混淆概念,知识点掌握不牢,没有建立知识体系。数学概念是学生理解、掌握数学知识的首要条件,也是进行计算和解题的前提。概念不清,就会导致思维混乱,也就无法正确解决相关问题[1]。
在小学数学概念教学中结合思维导图帮助学生找到知识点之间的联系,帮助学生了解概念的内涵和外延,能够变复杂为简单,促使学生主动地参与学习,发展学生的思维品质,提高课堂教学效率。
1 基于思维导图梳理概念的联系与区别
数学概念具有很强的逻辑性,理清了概念间的逻辑关系,学生思维的严谨性会有所提高。对于一些相关联又易混淆的数学概念,学生很容易出错,利用思维导图讲授数学概念,能够帮助学生理解不同概念之间的联系与区别。下面以三年级下册“认识面积”教学为例,梳理面积和周长之间的逻辑关系。
教学一开始,教师可通过引导学生看甲骨文中“面”的演变过程,引入数学中的“面”。接着通过让学生摸一摸、比一比、找一找,感受面是有大小的,了解物体表面的大小就是物体的面积。同时介绍曲面,把曲面变成平面可以采用化曲为直的思想。让学生感知体上有面,通过摸一摸和描一描等方式初次感受面积和周长的区别与联系。设计对比封闭图形和不封闭图形,让学生感知封闭平面图形的大小就是平面图形的面积。再设计点动成线、线动成面的活动,使学生理解点线面之间的关系。然后教师出示几组图形,学生发现对于相差比较大的图形,可以通过观察法比较其面积;对于面积相差不大的图形,可以用重叠法比较;还可以通过数方格的方法来比较面积的大小。测量长度和面积都是用小单位去测量大单位,积小面,成大面。最后教师出示面积为15个大方格的图形和面积为16个小方格的图形,让学生感知要用同样大小的方格去测量,这样标准才能统一,统一的标准就是后面要学习的面积单位。
关于周长和面积的关系,教师可设计以下环节:
1.1 对折1次
把长6厘米,宽4厘米的长方形对折一次,学生发现有以下两种情况(对角折不考虑),如图1所示。
通过计算学生发现左边图形的周长是:(6+2)×2=16(厘米);右边图形的周长是:(3+4)×2=14(厘米)。学生发现:面积相等的两个图形,周长不一定相等。
1.2 再次对折,剪去25%
通过转化,学生发现图2中左边的图形可以转化成右边的图形,周长不变,面积却变了。
1.3 凹凸对比
学生发现:如图3,周长相等的两个图形,面积不一定相等。
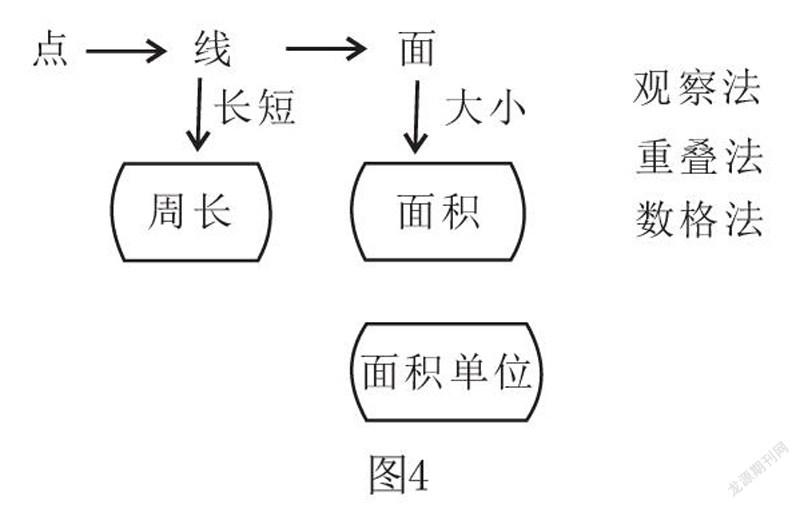
最终形成本节课的思维导图,如图4所示。
2 基于思维导图构建知识间的结构框架
学习一个新的概念时,教师要让学生形成知识框架,能够知道这个知识的内涵和外延。在建构知识框架时,不仅要联系旧知识,完善概念体系,还要引导学生应用相关概念。数学知识往往不是孤立的,它和其他知识或多或少有著一定的关联。
如在教学“多边形面积”时,教师可以让学生通过剪切、平移,把平行四边形面积转化成长方形面积,转化前后面积不变,平行四边形的底相当于长方形的长,平行四边形的高相当于长方形的宽,通过长方形的面积公式推导出平行四边形的面积公式,也就是平行四边形的面积=底×高,同时复习三角形和梯形的面积推导公式。从而按照学习的方向和转化的方向,理清新旧知识的联系。
教师可以以上底为3厘米,下底为5厘米,高为4厘米的梯形为例,让学生计算其面积。学生计算得到:(3+5)×4÷2=16(平方厘米)。
思考1:如果使这个梯形的上底不断地缩短,直至没有,最后会变成什么图形?生:三角形。学生计算得到:5×4÷2=10(平方厘米)。
思考2:如果使这个梯形的上底不断地变长,直至和下底一样长,最后会变成什么图形?生:平行四边形。学生计算得到:5×4=20(平方厘米)。
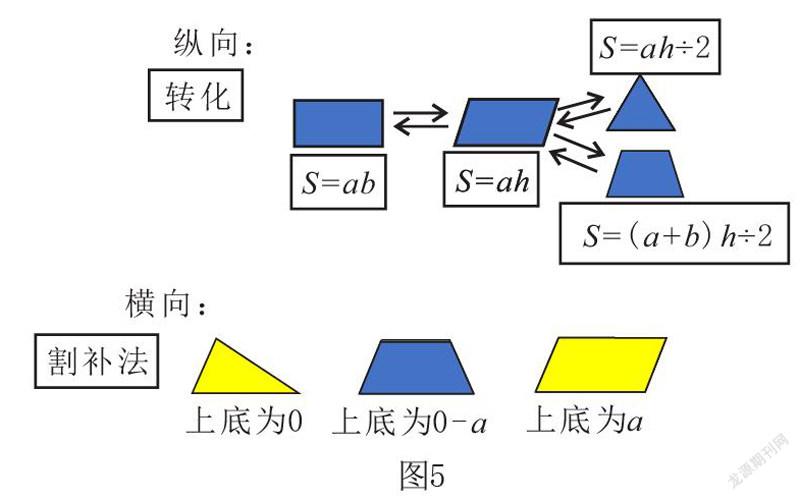
学生通过观察发现,当梯形的上底为0时,梯形就变成了三角形,当上底和下底一样长时,就变成了平行四边形。看似不一样的计算公式,归根结底还是可以用s=(a+b)h÷2来表示。在变与不变中,教师渗透了极限的思想,帮助学生理清三个图形面积之间的关系。最终形成思维导图,如图5所示。
3 基于思维导图发展学生的概括能力
小学生的概括和总结能力比较薄弱,在概念教学中引入思维导图,就可以让学生在学习过程中发散思维,加深学生对数学知识的理解和认识。这样学生就能主动地把学过的知识组成富有逻辑性、结构分明的知识体系,从而获得概括能力和核心素养的提升。
如在教学“用字母表示数”时,学生根据正方形的周长=边长×4,得到用字母表示就是c=4a。
师:每辆车有4个轮子,4a又表示什么?
生:4辆车一共有多少个轮子。
师:汽车每小時行a千米,4a又表示什么?
生:4小时一共行驶的路程。
师:你有什么发现?
生:虽然情境不同,但都可以用4a表示。
师:为什么都可以用4a表示呢?
生:因为每种情况下都存在着4倍关系。
师:你觉得4a还可以表示什么情况呢?学生发散思维。
师:一个简单的4a,就能表达所有这样4倍关系的一类情况。
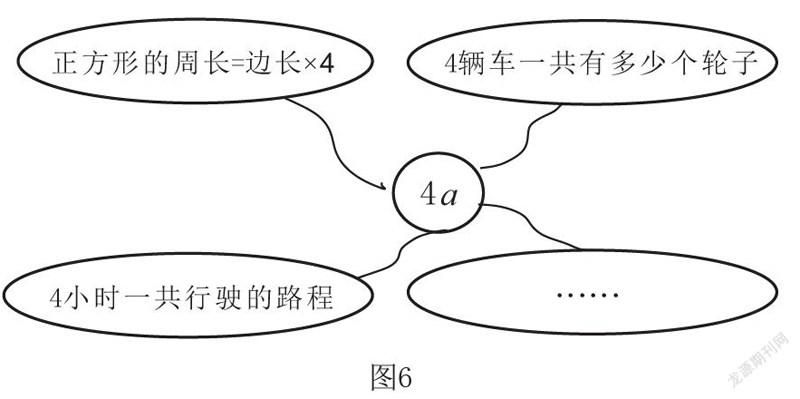
由此可形成思维导图,如图6所示。
4 基于思维导图培养学生的数学思维
教师不仅可以在课上引入思维导图,还可以在课后让学生以思维导图的形式整理所学新知。如果学生习惯了通过思维导图进行概念的学习,也就能主动地建构新的知识体系,培养数学思维。
如笔者在教学“间隔排列”时,首先引导学生理解什么是间隔排列,通过让学生动手操作穿珠子,学生发现有4种不同形式的穿珠方式。按颜色排列分别是“红蓝红蓝红蓝……”“红蓝红蓝红蓝红……”“蓝红蓝红蓝红……”“蓝红蓝红蓝红蓝……”。
接着学生通过研究珠子的个数发现这4种情况其实可以分成2种:也就是两端是相同颜色珠子的情况和两端是不同颜色珠子的情况。两端珠子颜色相同时,间隔排列的珠子数相差1;两端珠子颜色不同时,间隔排列的珠子数相等。然后对教材中的兔子和蘑菇、篱笆和树桩、手帕和夹子的情境进行验证,发现这样的规律:两端相同时,间隔排列的物体数量相差1;两端不同时,间隔排列的物体数量相等。接着学生把珠子围成一圈,发现围成的珠子数是相同的。最后教师可这样启发学生的数学思维:同学们,今天我们一起学习了间隔排列,如果照这样想下去,你还会想到什么样的排列呢?生:一二间隔排列,一三间隔排列,二四间隔排列……
由此形成思维导图,如图7:
总之,在小学数学课堂中借助思维导图进行概念教学,可以帮助学生整理信息,建构知识框架,突破教学重难点,增强学生学习的主动性,发展学生的数学思维。在课堂教学中,教师可以多用、巧用、善用思维导图,帮助学生进行思维导图的建构,从而提高学生的数学素养。
【参考文献】
[1]陈志强.浅谈思维导图在小学数学教学中的应用[J].名师在线,2021(16).
【作者简介】
于婷婷(1989~),女,汉族,江苏盐城人,本科,小学一级教师。研究方向:小学数学。
