锥摆扫一体化空间相机成像模式设计

支 政 ，曲宏松 ，李 静 ，张贵祥

（1. 中国科学院长春光学精密机械与物理研究所，吉林长春130033；2. 中国科学院大学，北京 100049；3. 中国科学院天基动态快速光学成像技术重点实验室，吉林长春130033；4. 北京跟踪与通信技术研究所，北京 100094）

1 引 言

空间遥感因其独特的优势，不仅在资源勘测、防灾减灾、环境治理等民用方面得到了广泛应用，同样也在导弹预警、海洋监视、战场监视、侦查及定位等军用领域发挥重要作用。随着空间对地观测技术的发展，空间相机的地面分辨率越来越高，但受到卫星载荷的体积和质量的限制，多数相机的地面覆盖宽度却相对较窄，这使得空间相机的应用在很大程度上受到了限制［1］。现有的遥感卫星大多数只能平行于飞行轨迹被动推扫成像，幅宽较窄。实际工程中，在保证高分辨的基础上增大幅宽，人们通常采用多片CCD拼接以增大有效视场，或采用多台视场重叠的线阵CCD 相机对地组合成像等方法［2-3］。这些方法虽然增大了视场，但是也增大了载荷体积。因此，敏捷成像性能的提高成为遥感卫星实现高分辨大视场的有效途径［4］。

目前，成像模式相对较少，敏捷卫星的飞速发展，导致原有的成像模式已经不足以发挥出敏捷卫星的特点。张新伟等利用敏捷卫星的姿态控制能力，提出了多目标成像、立体成像、宽幅拼接成像和动态扫描成像4 种典型的工作模式，并明确了卫星工作模式与姿态机动能力之间的关系［5］。基于线阵CCD 推扫成像原理，黄群东等分析了姿态机动过程中的像移问题［6］。为了增大覆盖幅宽，余婧等针对长宽均明显大于相机幅宽的区域目标的成像观测，设计了敏捷卫星同轨沿轨方向多条带拼幅成像模式［7］。为了提高对感兴趣目标区域的成像效率，于龙江等针对敏捷卫星对一轨内任意走向条带目标的成像观测需求，设计了一般轨迹主动推扫成像模式［8］。针对传统卫星调度方法难以满足应急观测强时效性的问题，章登义等提出一种针对敏捷成像卫星的调度方法，对提升应急条件下高分辨率图像的获取能力具有十分重要的意义［9］。单轨调度可以有效地提高高分敏捷卫星垂轨的覆盖幅宽，但是牺牲了沿轨方向的覆盖长度，为此敏捷卫星的新型成像模式成为了研究的聚焦点。针对卫星广域搜索成像需求，宋明珠等提出了一种新型环扫成像模式［10］。李宪圣等针对动中成像中复杂多变的情况，提出了空间相机在轨成像模式来获得高质量的图像［11］。Barschke 等同样针对高机动敏捷卫星的姿控能力，设计了4 种工作模式，与张新伟等的不同之处在于条带扫描的方向可以是非沿轨方向［12］。Tonetti 等针对敏捷卫星对点观测序列问题，利用西班牙DEIMOS-2，设计了卫星能力分析与全自动任务规划工具（Capacity Analysis and Mission Planning，CAMP），该工具利用敏捷卫星的姿控能力进行反复调度，并且选择时间点实现任务规划的最优化［13］。Tanpattanaku 等提出了多用户、多任务需求下的敏捷卫星多目标任务规划模型［14］。综上可知，国外学者的研究重点在轨道调度设计和优化上，而国内学者除了进行轨道方面的研究，还进行了新型成像模式的探索。

本文针对遥感卫星高分辨相机难以实现超宽覆盖，考虑现有成像模式地面分辨率、卫星载荷体积质量和地面覆盖宽度三者互相制约的问题，设计了一种高分相机实现超宽覆盖的锥摆扫一体化成像模式。在该模式下，载荷轨道运动、卫星平台的轨道运动和自旋运动相结合的多维复合运动，以一个成像单元运动来代替多个成像单元拼接，在不影响成像分辨率的前提下，缩小探测器的靶面及尺寸，实现覆盖视场的扩展。

2 锥摆扫一体化成像模型

2.1 坐标系定义

锥摆扫一体化成像模型的设计需要建立一系列模型，这些模型在不同的坐标系下建立，这些坐标系满足物面到像面的映射关系，如图1所示［15］。

图1 锥摆扫一体化成像模型的坐标系映射关系示意图Fig.1 Mapping relation diagram of reference coordinate systems for core-pendulum scanning integrated imaging model

（1）地心惯性坐标系I（I1，I2，I3）

地球惯性坐标系以地心为原点，I3轴在赤道面内，指向轨道面和赤道面的交点，I2轴指向北极，I1 轴垂直于I2和I3两轴形成的平面。

（2）地球坐标系E（E1，E2，E3）

地球坐标系固联于地球，原点与I系原点重合，E2轴与I2轴重合，指向北极，地球坐标系在I系内绕I2轴逆时针方向以角速度ω自转。

（3）卫星轨道坐标系B（B1，B2，B3）

原点在卫星轨道上，以卫星质心为原点，B1轴指向轨道前向（卫星线速度方向），B3轴过I系原点指向天顶，B2轴与轨道面垂直（B1，B2轴在轨道面内），B系在I系内，沿轨道做以角速度为Ω的轨道运动。

（4）地理坐标系G（G1，G2，G3）

地理坐标系G3轴与B3轴重合，沿B3轴平移“-（H-h）”（航天器到星下点的真高度），即得到G系。G1，G2轴平行于B1，B2轴。

（5）卫星坐标系S（S1，S2，S3）

卫星坐标系原点于B系原点重合，卫星无姿态运动时，S系与B系重合。卫星有姿态运动时，以三轴姿态角（横滚角φ、俯仰角θ和偏航角ψ）分别绕B1，B2，B3轴旋转。

（6）相机坐标系C（C1，C2，C3）

相机坐标系原点为相机物镜主点，当相机无倾斜安装时与S系重合。

（7）像面坐标系P（P1，P2，P3）

像面坐标系原点在像面中心，C系沿C3轴平移f（相机焦距），即得到P系，P1和P2组成像面。

2.2 锥摆扫一体化成像原理

锥摆扫一体化成像模式主要解决传统成像模式下地面幅宽受限，及增大幅宽和探测器靶面导致的载荷体积越来越大的问题。传统成像模式中，空间相机相对卫星平台静止，光轴与卫星坐标系S3轴平行或成一定角度倾斜安装，实现推扫成像。在这种成像模式下，为了进一步增大地面覆盖幅宽，只能通过牺牲分辨率，减小焦距，或者通过牺牲载荷体积，进行探测器拼接成像来扩大幅宽，如图2 所示。锥摆扫一体化成像模式通过相机往复的摆扫运动，来代替探测器拼接扩大像面的方法；通过卫星平台锥扫运动来减小焦距，在不牺牲分辨率及载荷体积的前提下，实现宽覆盖、长覆盖的广域搜索。

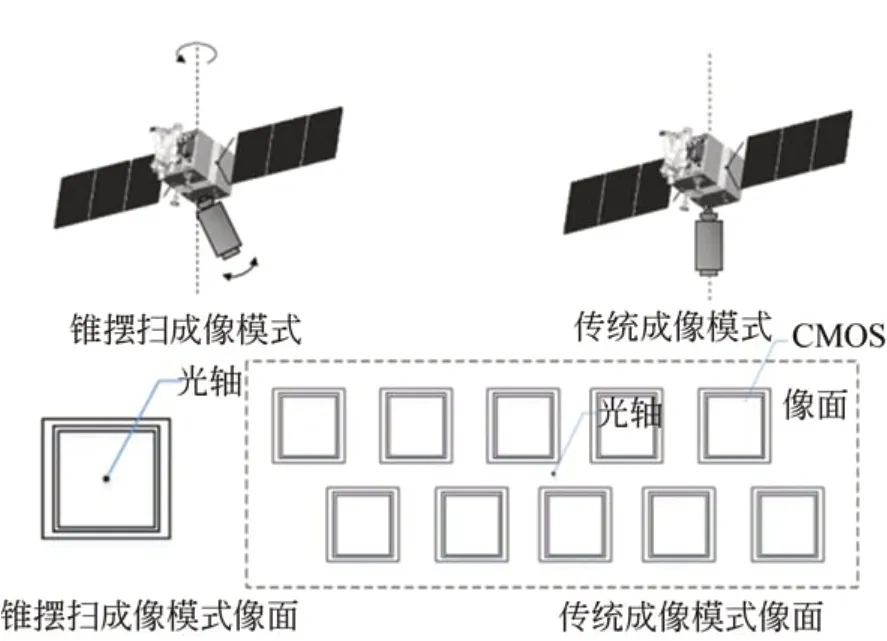
图2 锥摆扫成像模式与传统成像模式的像面Fig.2 Image planes of cone-pendulum scanning imaging model and traditional imaging model

锥摆扫一体化成像模式的结构示意图如图2所示，与传统成像模式星下点成像不同，锥摆扫一体化成像模式光轴在相机开拍时一直在运动，故定义光轴与地面交点为轴地点。相机应用单片CMOS 传感器成像，并且以倾角α倾斜安装在卫星平台上，当卫星平台绕中轴自旋时，结合后期图像拼接，由推扫条带变为螺旋式条带轨迹，就可以在横向上大大增加成像幅宽。同时，相机以钟摆式往复摆动，轨迹变为折线式螺旋线，轴地点轨迹如图3 所示，S点为起点，E点为终点，一个周期的摆动成像如图中a-b-c，具体成像顺序如图4 所示。

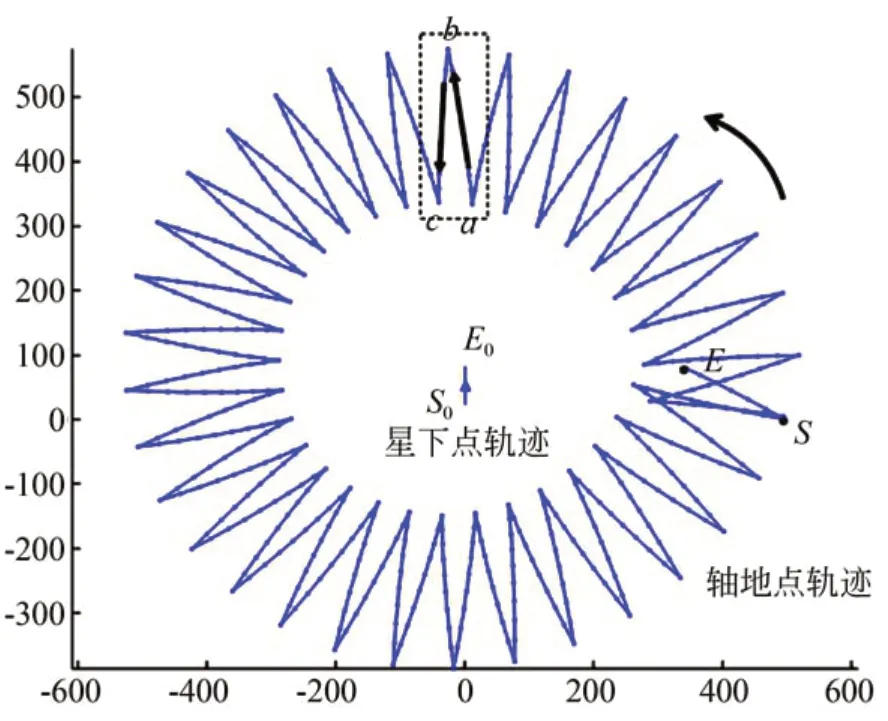
图3 轴地点与星下点轨迹示意图Fig.3 Locus diagram of cross point of optical axis with ground and sub-satellite point

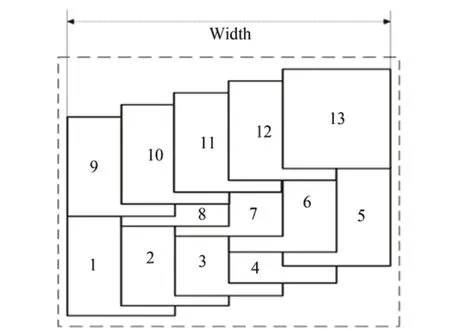
图4 一个摆扫周期内成像示意图Fig.4 Schematic diagram for imaging in single pendulum scanning period

光学系统结构形式主要有反射式、折反射式和折射式3 种结构形式［16］。同轴反射式和折反式光学系统的视场角较小，通常不大于3°，且存在中心遮拦问题，能量利用率小，不能满足视场要求。而离轴反射式光学系统体积大，不适用于本设计的轻量化和小型化。折射式结构具有大视场、能量利用率高、结构简单和便于装调等优点，能够更好地满足锥摆扫一体化成像模式关于大视场、轻小型的要求。

锥摆扫一体化成像模式通过合理选取相机安装倾角、卫星平台旋转速度、相机摆动机动速度和轨道高度等参数，可以完成目标区域的完整覆盖；通过合理地规划成像方式和成像参数选取，可实现宽覆盖下数据量的最小化，并且通过合理的曝光时间控制，可以降低像移对成像质量的影响。利用锥摆扫一体化成像模式，可将成像幅宽由十公里量级提升到千公里量级，并且不影响纵向的覆盖范围和载荷平台的承重问题。这是原有的成像模式无法企及的特点，在广域搜索等特定场合可发挥关键作用。

2.3 锥摆扫一体化地面轨迹设计

锥摆扫一体化成像过程中，相机倾角α、卫星平台旋转速度、相机摆动机动速度、轨道高度及单次摆动成像帧数等参数，都会对其地面覆盖轨迹模型产生影响。如果各参数选取不合理，则会导致地面目标重复覆盖或地面目标覆盖遗漏的问题。

首先进行地面轨迹模型设计。与传统小幅宽成像不同，千公里超大幅宽条件下，需将地面视为球面。假设轨道高度为H，相机焦距为f，相机光轴倾角为μ（包括相机倾角α和相机摆扫倾角β），相机视场角为δ，锥摆扫成像模式初始状态的几何关系如图5 所示。该时刻下卫星平台的轨道速度vt和卫星平台旋转角速度ωs分别如下：

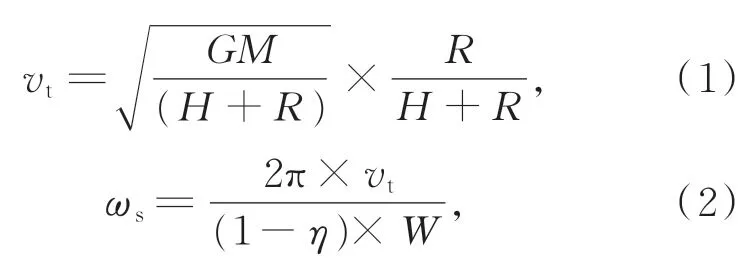
式中：GM为地心引力常数，R为地球半径，η为帧间重叠率，通常选取10%，W为摆扫一周期的宽度，其关系式为：

根据图5 所示几何关系，式（3）中各参数的表达式如下：

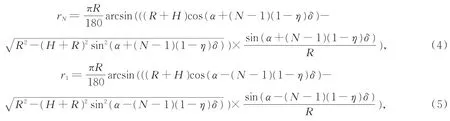
式中：N为摆扫半个周期的成像次数，δ为相机视场角。

在该轨道高度和相机倾角下，一个摆扫周期内，若远视场点可实现搭接，那么近视场点也能实现搭接，由此计算出摆扫运动的转动角速度ωc为：

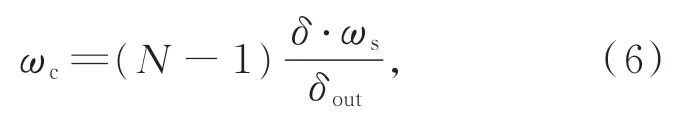
式中δout为上下边界上远视场点像素间的夹角。

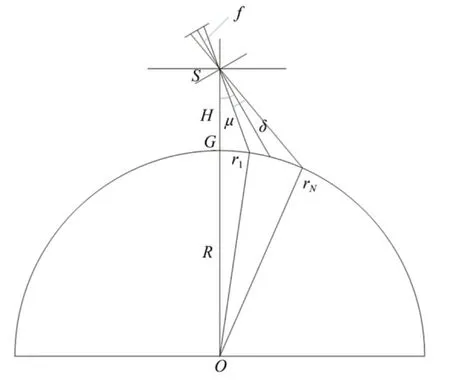
图5 锥摆扫成像的几何关系Fig.5 Geometry relationship of cone-pendulum scanning imaging model

锥摆扫一体化成像时，当载荷相机、帧间重叠率、轨道高度和摆扫半周期成像次数确定时，由式（1）～式（6）计算得到的卫星旋转速度和摆扫运动的转动角速度为最佳速度，可保证地面覆盖的合理性。

2.4 锥摆扫一体化成像参数计算

曝光时间与成像帧频是影响成像质量的重要参数，直接影响着拍摄图像的地面清晰度和图像的重叠率，以及拼接难度。

锥摆扫一体化成像相机应用CMOS 传感器作为传感器元件。为了减小像移的影响，保障成像质量，在曝光时间内的像移量要小于一个像元。假设像元尺寸为a×a，此时的曝光时间需要满足：

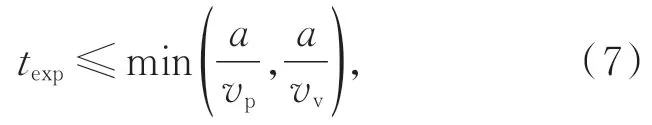
式中vp，vv分别为沿轨和垂轨方向的像移分速度。

传统成像模式中，星下点为光轴与地面交点，在t时刻的像移速度可由七次坐标变换求得。锥摆扫成像与传统成像模式的不同之处在于：增加了锥扫和摆扫两个运动，并且相机与卫星有一个安装倾角，在变换过程中需要考虑锥摆扫产生的像移影响和安装倾角的影响。地理坐标系到像面坐标系的变换过程如图6 所示。

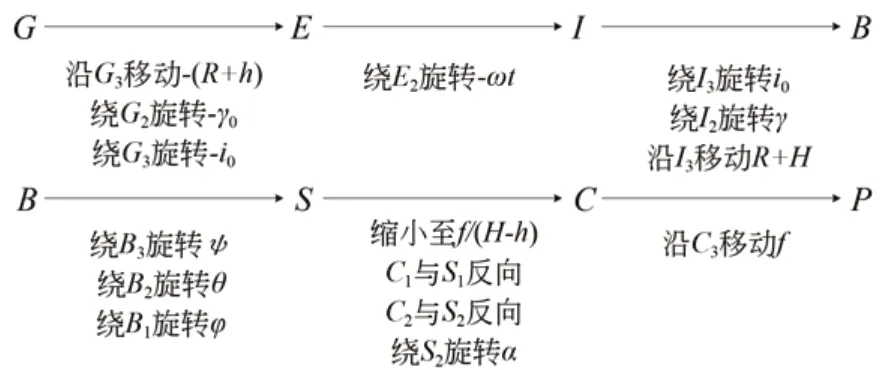
图6 地理坐标系到像面坐标系的坐标变换过程Fig.6 Process of coordinate transformations from geographic coordinate system to image plane

图 6 中，R为地球半径；H为卫星轨道高度；h为目标景物高程；i0为轨道倾角；f为相机镜头焦距；γ=γ0+vt·t；γ0为卫星星下点的地心角；α为相机安装倾角；ψ，θ，φ分别为卫星坐标系相对于轨道坐标系的偏航角、俯仰角和横滚角。

分别考虑轨道运动、锥摆扫运动和地球自转影响下的像移速度，综合总像移速度来计算合理的曝光时间。当像面上远离卫星的最外侧像素点满足在曝光时间内，像移量没有超过一个像元，那么内侧像素点均满足条件。

轨道速度引起的像移速度vf1与轨道速度vt的关系为：

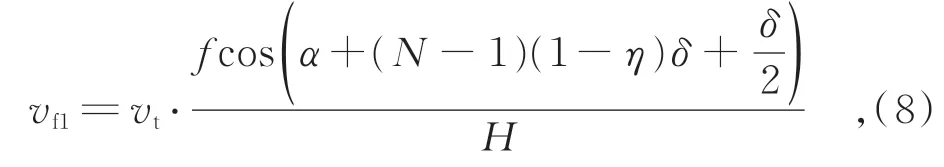
式中vf1为沿轨方向。

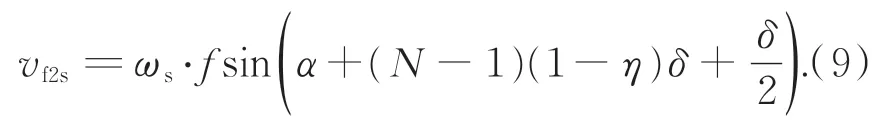
vf2s为平行于地表的任意方向。摆扫运动引起的像移速度vf2c与摆扫角速度ωc的关系为：

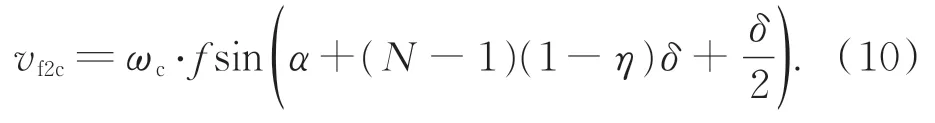
vf2c方 向 垂 直 于vf2s。

地球自转影响的像移速度相比于上述两个引起的像移速度非常小，并且方向为垂轨方向，所以忽略不计。

由式（8）～式（10）可知，沿轨方向速度vp＞垂轨方向速度vv，所以沿轨方向的速度范围为：

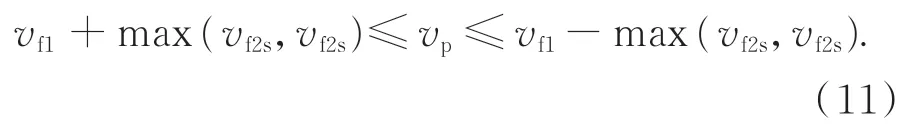
以远视场像为基准（远视场像素拼接，内视场像素必然拼接），卫星旋转360°所需的成像帧数为：

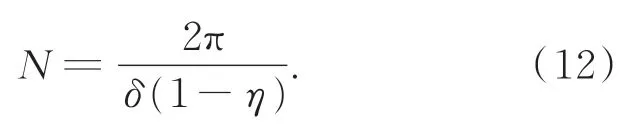
此时，相对应的环扫帧频为：

3 锥摆扫一体化成像仿真

根据上述分析，假设卫星轨道高度为500 km，此时的轨道速度vt近似为7.06 km/s；帧间重叠率η取 10%，CMOS 选取像元尺寸为 2.5 μm×2.5 μm，像元个数为5 120×5 120；相机安装倾角α为 30°，焦距f为 360 mm，视场角δ为 2.04°，摆动半周期内成像帧数N为10。

锥摆扫成像模式在该参数下的地面覆盖仿真如图7 所示。此时卫星的旋转角速度ωs为10.5（°）/s，摆扫角速度为 69.7（°）/s，曝光时间为6 μs。单片CMOS 作为像面，进行星下点推扫，地面覆盖仿真如图8 所示。

语文教育是任何学科教育的基础，它在学生素质培养中有不可估量的作用。语文课是工具性和人文性的统一，它的作用也可以从这两个方面得到体现。

由图7 和图8 可以看出，传统星下点推扫地面覆盖宽度大概为20 km，而锥摆扫一体化成像模式下地面覆盖宽度可以达到约1 200 km，幅宽明显增大，并且覆盖完全无遗漏。

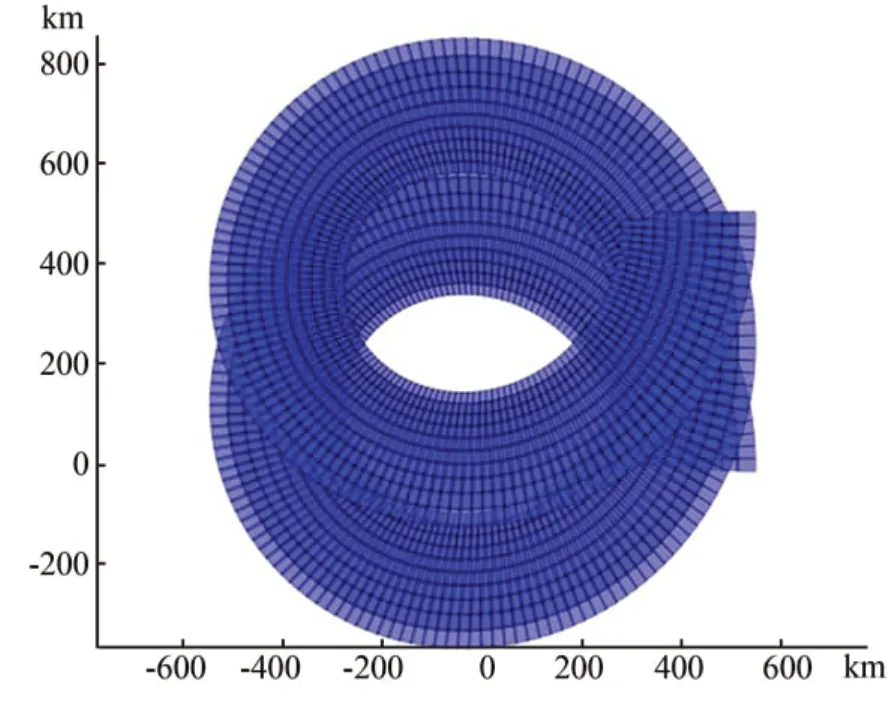
图7 锥摆扫成像模式地面覆盖仿真Fig.7 Ground cover simulation of cone-pendulum scanning imaging model

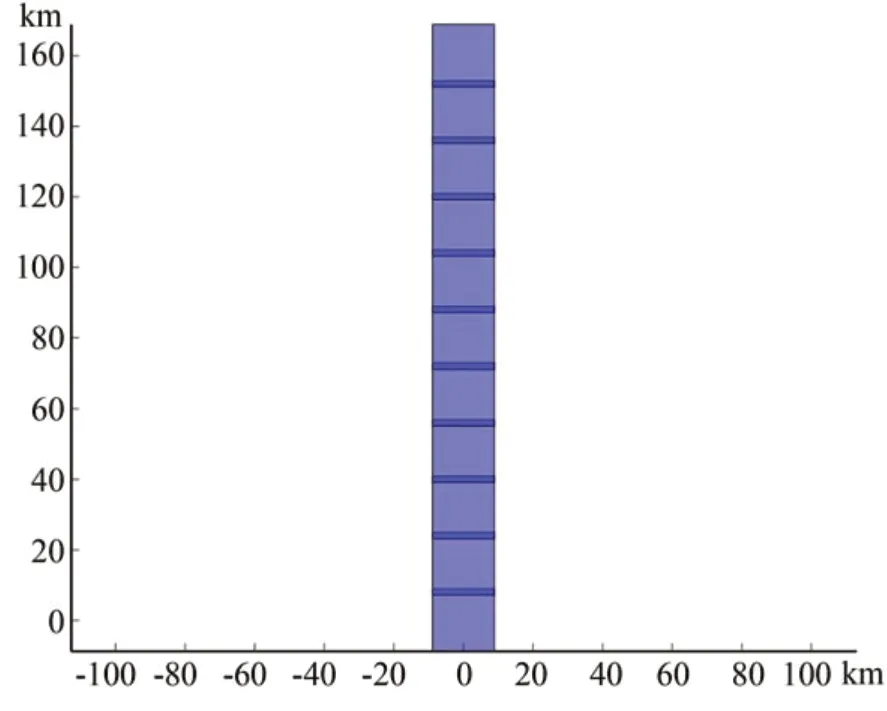
图8 星下点成像模式地面覆盖仿真Fig.8 Ground cover simulation of sub-satellite point scanning imaging model

4 锥摆扫一体化成像参数分析

4.1 地面覆盖宽度

空间相机锥摆扫一体化成像的主要目的是扩大单轨搜索下的地面覆盖，最重要的参数就是地面幅宽。传统成像模式下，幅宽很小，对应的地心角也很小，可以将地面简化为平面，相应的地面覆盖宽度为：

式（14）、式（15）分别为星下点成像和侧摆α成像时的地面覆盖宽度。当单轨且轨道高度一定时，传统的成像模式的地面覆盖宽度仅由单帧幅宽决定。假设轨道高度H为500 km，像元尺寸a为 2.5 μm，焦距为360 mm，垂轨像元数M为5 120，则星下点成像时地面覆盖宽度为35.5 km。

而当采用锥摆扫一体化成像模式时，地面覆盖宽度不再仅由单帧幅宽决定，而是由增加的锥摆扫二维运动绕着卫星平台旋转划过沿垂轨方向的弦长决定。锥摆扫一体化成像模式由于超宽覆盖，不能像传统成像模式一样简化地面模型，需要将地面作为球面来建立模型，对应的锥摆扫一体化成像模式下的最大地面覆盖宽度表达式如下：

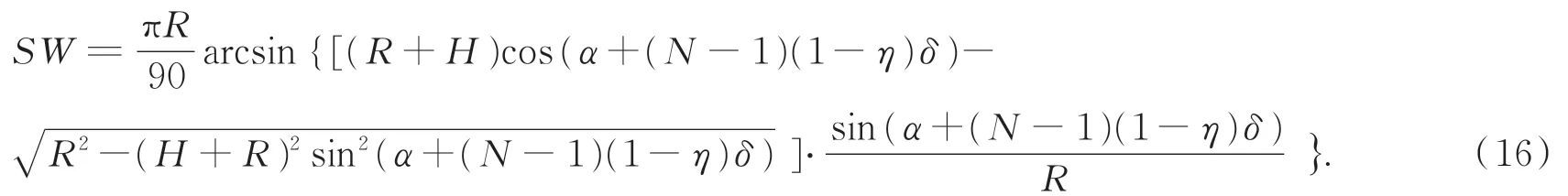
当轨道高度确定时，影响地面覆盖宽度的有安装倾角α和半周期成像帧数N。分别以安装倾角α、半周期拍摄帧数N作为自变量对锥摆扫一体化成像模式下的地面覆盖宽度变化进行分析。此时的相机视场角为：

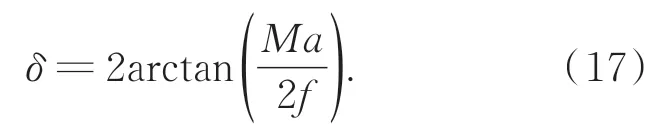
取半周期成像帧数N为10，地面幅宽随相机倾角的变化曲线如图9 所示。

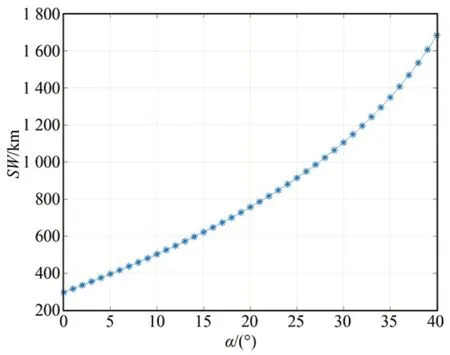
图9 地面幅宽随相机安装倾角α 的变化曲线Fig.9 Curve of swath width changes with camera installed inclination angle

表1 特定相机安装倾角下地面幅宽Tab.1 Swath width with special camera installed inclination angle

从图9 及表1 中可以看出，地面幅宽随相机安装倾角α的增大而增大，当安装倾角α分别为0°，10°，20°，30°，40°时地面幅宽分别是传统星下点成像（35.5 km）的 8.4，14.2，21.3，31.1，47.4倍。取相机安装倾角为30°，地面覆盖宽度随摆扫半周期成像帧数N的变化曲线如图10 所示。

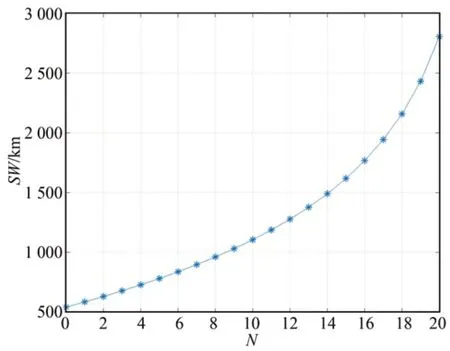
图10 地面幅宽随摆扫成像帧数的变化曲线Fig.10 Curve of swath width changes with pendulum scanning imaging frames

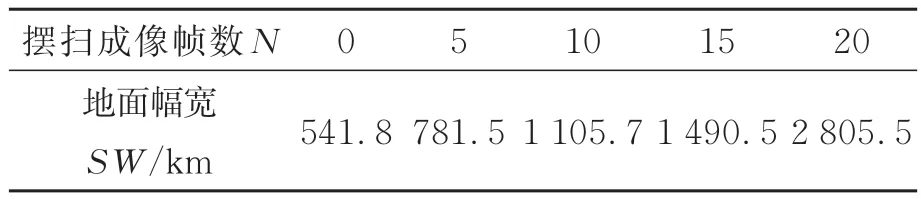
表2 特定摆扫成像帧数下的地面幅宽Tab.2 Swath width with special pendulum scanning imaging frames

从图10 及表2 中可以看出，地面幅宽随摆扫半周期成像帧数N的增大而增大，当半周期成像帧数N分别为 0，5，10，15，20 时，对应的地面幅宽分别为星下点成像（35.5 km）时的15.3，22.0，31.1，42.0，79.0 倍。

由于锥摆扫一体化成像模式显著提升了地面幅宽，相比于传统成像模式，重访周期也有显著提升。美国WorldView-1 的轨道高度为500 km，单颗卫星的重访周期为5 d。而锥摆扫成像模式在相机安装倾角为30°、摆扫成像帧数为10的条件下，地面幅宽为1 105.7 km，赤道附近某点最短的重访周期为0.5 d，增大了10 倍。

4.2 地面像元分辨率

与传统成像模式相比，锥摆扫一体化成像模式由于相机安装倾角和增加的二维运动，其地面像元分辨率随着对面目标与星下点距离的变化而变化。在相机坐标系C下，建立传感器上各个像元的地面分辨率的数学模型，相应关系如图11所示。

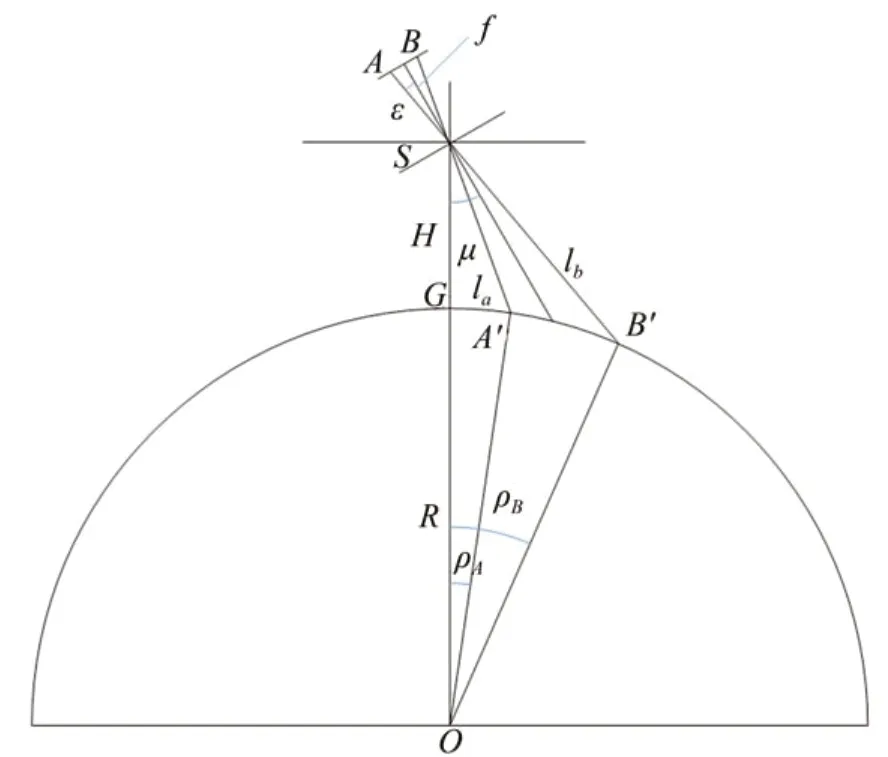
图11 像面单个像元与对应地物的几何关系Fig.11 Geometry relationship between single pixel on image surface and corresponding ground target

光轴处像元对应的地面分辨率为：

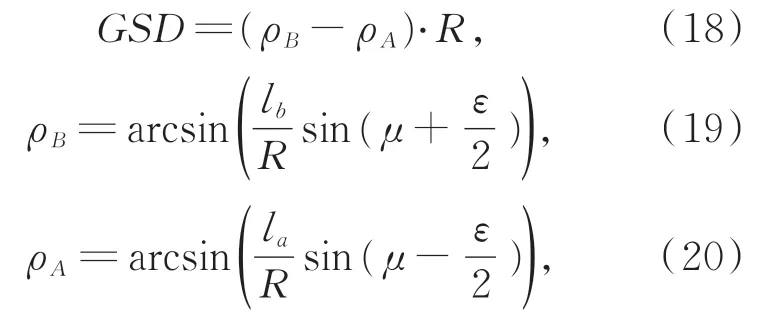
式中：la，lb分别为像素边界A，B点在地面的投影到相机的距离；ε为任一像素的视场角，表达式中M为垂轨像元数；μ为光轴倾角，μ=α+β。

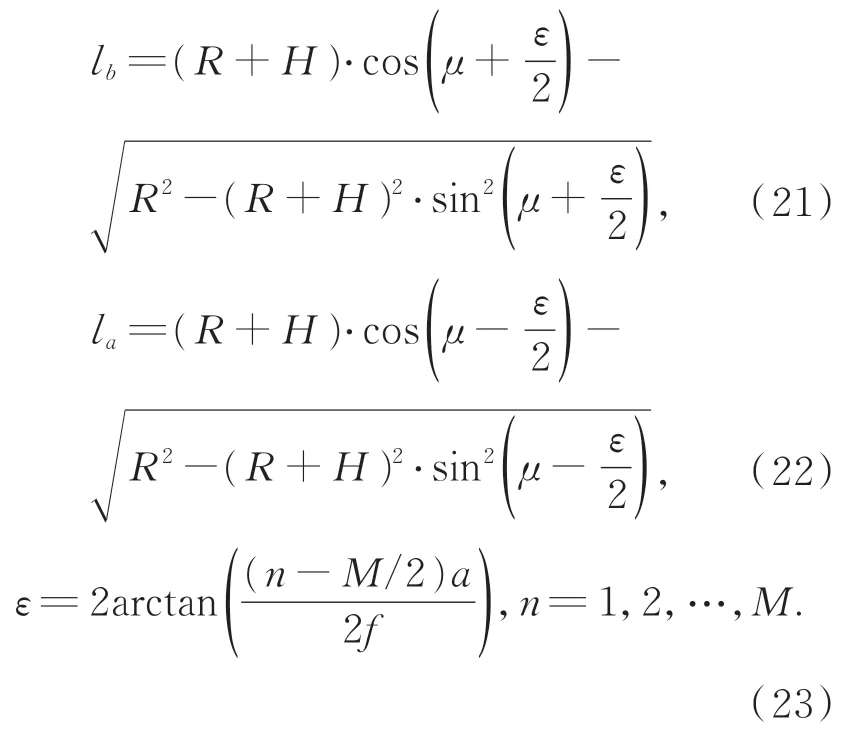
对像面内径向和垂直径向各像素点对应的地面像元分辨率变化进行分析。地面分辨率在径向和切向的区别在于径向方向有相机安装倾角和摆扫倾角的影响，即切向的光轴倾角μ=0。假设卫星轨道高度H为500 km，像素尺寸a为2.5 μm，焦距为 360 mm，摆扫半周帧数N为 10，垂轨像元数M为5 120。像面切向方向各像素点的地面像元分辨率如图12 所示。以相机安装倾角为自变量，分别在 0°，10°，20°，30°，40°倾角下，相应的像面上径向方向上各像素点的地面分辨率如图13 所示，各安装倾角下相对α=0°时的扩大倍数如表3 所示。固定相机倾角为30°，摆扫帧数分别为 0，5，10，15，20 时，地面像元分辨率与像面径向方向的像素关系如图14 所示，各摆扫成像帧数相对N=0 时的扩大倍数如表4所示。

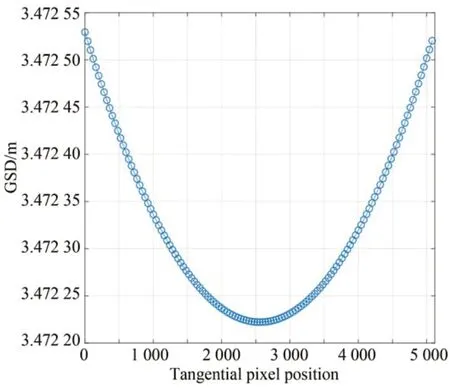
图12 地面像元分辨率随切向像元位置的变化曲线Fig.12 Curve of Ground Sample Distance（GSD）changes with tangential pixel position

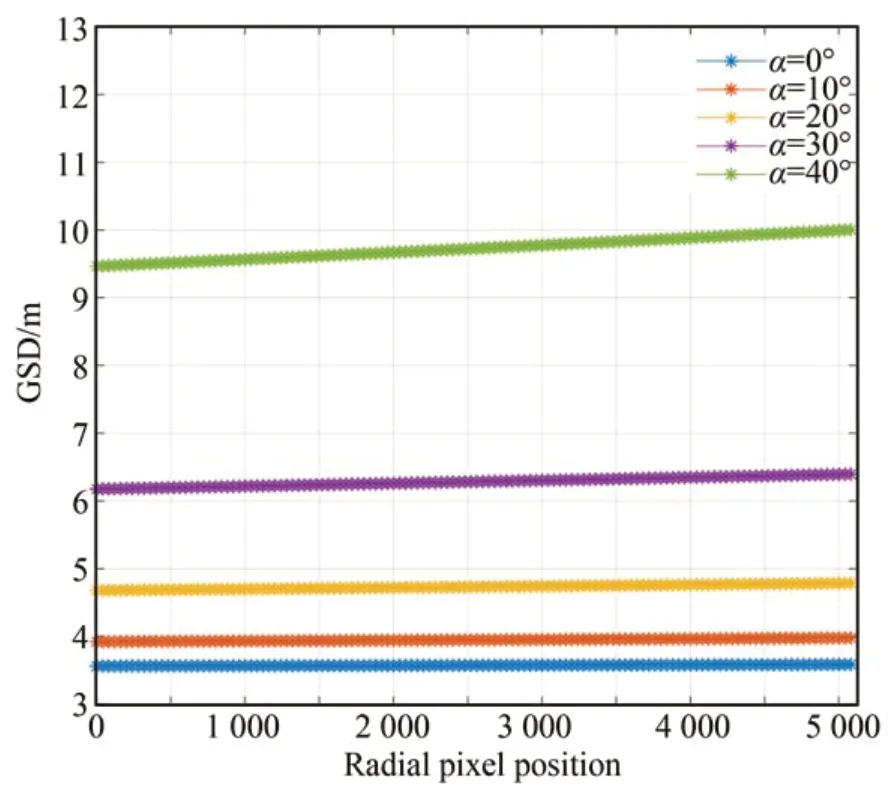
图13 不同安装倾角下地面像元分辨率与径向像素位置的关系曲线Fig.13 Curve of Ground Sample Distance（GSD）with radial pixel position at different camera installed inclination angles

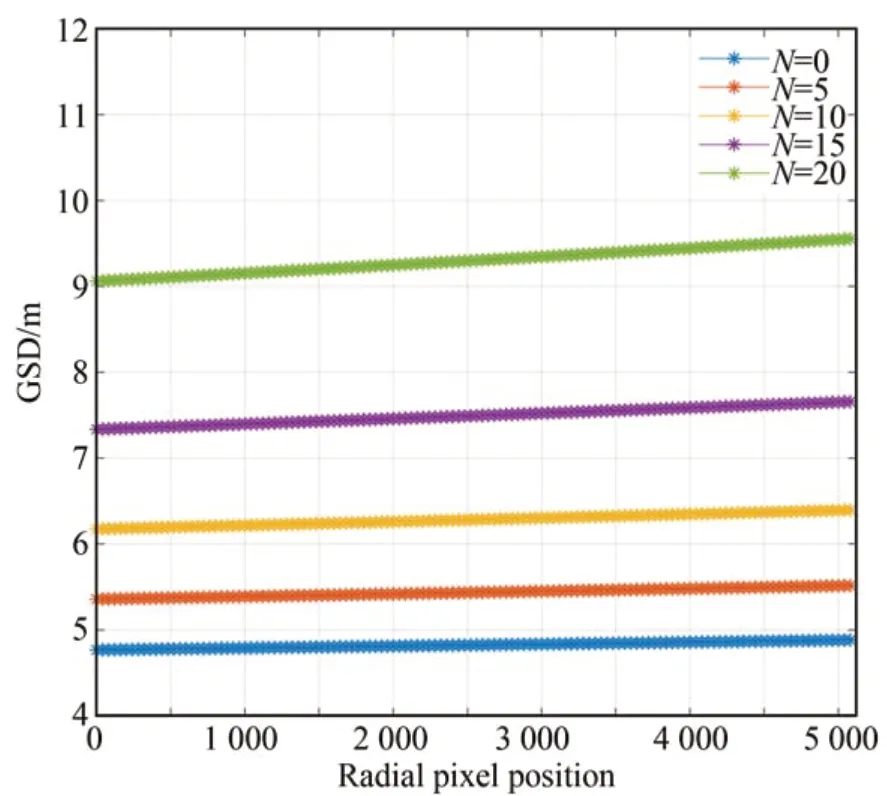
图14 不同摆扫帧数下地面像元分辨率与径向像素位置的关系曲线Fig.14 Curve of Ground Sample Distance（GSD）with radial pixel position at different pendulum scanning imaging frames

从图12～图14 可以看出，像面上切向方向，以中间像元为基准越靠近外侧，地面像元分辨率越大。在径向方向上，靠近星下点的像素点比远离星下点的像素点地面像元分辨率更小，且随着相机安装倾角、摆扫成像帧数的增大而增大。由表3 和表4 可知，地面像元分辨率与相机安装倾角和摆扫成像帧数并不呈线性关系，因此，在锥摆扫一体化成像模式中，需要根据实际情况对相机安装倾角和摆扫成像帧数进行分析选取，以保证地面像元分辨率满足成像需求。

表3 不同安装倾角相对0°安装倾角时地面像元分辨率的扩大倍数Tab.3 Expansion times of ground sample distance of different camera installed inclination angles relative to 0° installed inclination angel

表4 不同摆扫帧数相对0 帧时地面像元分辨率的扩大倍数Tab.4 Expansion times of ground sample distance of different pendulum scanning imaging frames relative to 0 frame

5 结 论

针对航天遥感地面像元分辨率和幅宽相互制约的问题，本文设计了锥摆扫一体化成像模式，让航天遥感能够在大覆盖的应用背景下发挥优势。该新型动中成像模式能够很好地兼容大视场、高分辨、轻小型的优点。首先对运动参数进行分析，后对成像参数进行计算，设计出最佳的地面轨迹覆盖模型。其次，进行模型覆盖仿真验证其合理性。最后，分析成像模式的地面覆盖宽度和地面分辨率的变化情况。仿真分析表明，锥摆扫一体化成像模式能够在完全覆盖和保证一定高分辨率的条件下实现千公里量级的超宽覆盖；在500 km 的轨道高度，360 mm 的焦距，2.5 μm 的像元尺寸，像元数为 5 120×5 120，摆扫成像10 帧，相机安装倾角30°下能达到1 105.7 km 的地面覆盖宽度。但是，由于摆扫速度过快，CMOS 传感器的曝光时间较短。本文研究目前处于理论推导和设计阶段，下一步研究要解决该模式下CMOS 传感器曝光时间较短的问题，并且基于该成像模式拍摄的特殊图像进行图像拼接以及后续图像处理，从而优化该成像模式的成像质量。