连续转速状态下卫星反作用飞轮微振动参数识别

杨 林 ，王岩松 *，魏 磊 ，胡自强

（1. 山东大学前沿交叉科学青岛研究院，山东青岛266200；2. 山东大学 空间科学研究院，山东 威海 264209）

1 引 言

随着航天技术的快速发展，光学遥感卫星正呈现出更高指向精度和更高分辨率的特点。近些年国际上的商业遥感卫星已经达到优于0.3 m的分辨率［1］。对于高分辨率遥感卫星来说，光学载荷对于卫星上的微小扰动十分敏感，微振动对成像质量的影响已经变得不可忽略。在反作用飞轮微振动作用下，光学遥感卫星在成像时会出现图像扭曲和模糊等问题［2］。

为降低卫星微振动的影响，主要采取的手段包括：降低干扰源的影响、优化星体传力路径以及隔振等方法［3-5］。反作用飞轮是航天器的姿态控制系统的执行机构之一，其性能影响着航天器姿态控制的精度。由于反作用飞轮在工作时受到转子动静不平衡、轴承缺陷、飞轮结构模态放大等因素的影响［6］，会激发出一系列复杂的谐波扰动，所以反作用飞轮是微振动的主要干扰源之一。对反作用飞轮力学机理以及其运转过程中的干扰特性的研究，对航天器微振动技术以及其抑制方法的研究具有重要的意义。对反作用飞轮的研究方法主要包括飞轮理论模型的建模［7］，飞轮干扰特性的经验模型的建立以及飞轮干扰特性及结构模态参数识别等［8-11］。通过飞轮参数识别方法可以直观地反应出飞轮干扰特性和结构模态的分布特点，并且能够反应出理论建模不能反应的真实特性，为后续飞轮的隔振方法研究、整星的微振动分析和试验提供基础。

当前应用范围较广的是恒定转速的飞轮参数识别方法，通常是利用一系列固定转速的干扰力/力矩数据，分析飞轮的干扰特性及模态参数［12］。此类方法仅能分析恒定转速下飞轮的模态参数和干扰力特性，为了得到飞轮在一个转速区间的干扰特性，需要通过大量的试验来获得不同转速情况下试验数据［13］，大大增加了工作量；并且，反作用飞轮在实际工作过程中，尤其在卫星姿态运动过程中，其转速并不是完全恒定的［14］，飞轮的干扰力为一段非平稳信号，此时利用传统的傅里叶变换方法得到的模态特性和干扰力特性将因转速的变化而变得不稳定。所以常规的恒转速下飞轮微振动参数识别方法是不能准确反应在轨工作状态的。

本文将建立一种非恒定转速运动状态下反作用飞轮的参数识别方法，可以利用非平稳信号识别出飞轮非恒定转速下的干扰力倍频特性以及模态参数。首先利用时频分析，将试验得到的飞轮非恒定转速下的干扰力非平稳信号，转化为时频分布函数，并通过转速与时间的对应关系，将时频分布函数转化为转频分布函数；之后建立飞轮的倍频特性识别方法，识别出飞轮的干扰力分布；最后建立非恒定转速飞轮的参数化的结构模态参数识别方法，识别出飞轮的结构模态。本文将通过干扰力测试验证所提出的方法，首先进行一次非恒定转速的干扰力测试得到飞轮干扰力试验数据，利用以上方法识别出该飞轮的干扰力分布特性和模态参数。通过结合倍频特性和模态参数，可以得到飞轮的转速-频率峰值点，预测飞轮干扰力最大值的分布情况。该方法将在保证一定精度的前提下，大大提升飞轮参数识别的效率。

2 反作用飞轮倍频特性识别

2.1 动力学模型

反作用飞轮的动力学模型可以表示为

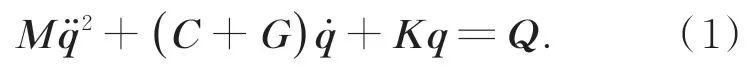
通过求解特征方程，可以得到反作用飞轮的无阻尼固有频率，可以表示为［13］：

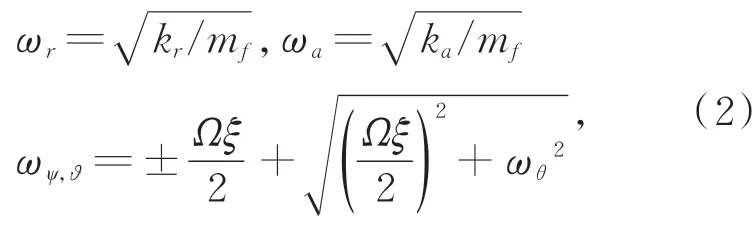
其中：ωr和ωa分别对应径向平动和轴向平动，ωψ，ϑ对应径向摇摆，Ω指飞轮转速，ξ指极惯性矩与径向惯性矩之比。从式（2）中可以发现，飞轮的摇摆模态是与飞轮转子速度相关的。

2.2 时频分析原理

对于固定转速的飞轮，其干扰力/力矩时间响应信号是一组平稳信号，通过Fourier 变换即可得到当前转速下飞轮各个方向干扰力的频谱。但当飞轮的转速不断变化时，飞轮干扰力信号的频谱特性是随时间变化的。因此传统的Fourier变换不再适应变转速飞轮干扰力/力矩频域特性分析。

时频分析方法是一种时变非平稳信号处理方法，能够将非平稳信号分解为由时间和频率二元变量决定的时频分布函数，以描述信号在不同时间和频率下的幅值分布密度［15］。时频分析方法可以直观的体现信号的频率变化特性，广泛应用于故障诊断和模态参数识别等领域。目前应用最为广泛的时频分析方法主要包括短时Fourier 变换（STFT）、小波变换（WT）、Wigner-Ville分布（WVD）等。以下将采用短时Fourier 变换作为飞轮响应信号的时频分析方法。

短时Fourier 变换的频谱可以表示为：

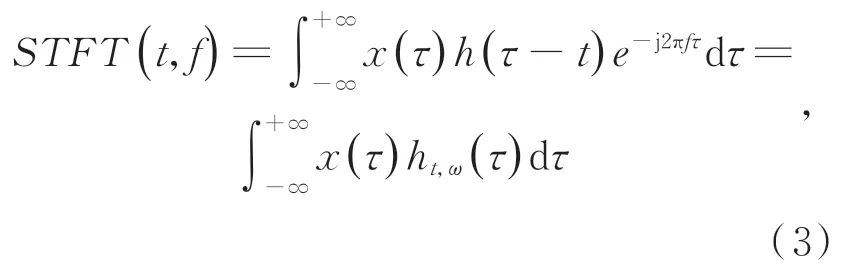
其中：x(τ)为被分析的时间信号，h(t)为窗函数，ht，ω(τ) =h(τ-t)e-j2πfτ为窗函数对应的基函数。

之后利用转速随着时间变化的函数，可以将时频分布谱的时间轴转化为转速轴，得到短时Fourier 变换在转速- 频率平面上的分布STFT(r，f)，功 率 谱 密 度 函 数 可 以 表 示 为G(r，f) =|STFT(r，f)|2。

2.3 倍频特性识别

飞轮的干扰力由一系列复杂的谐波和噪声构成。这些谐波包括基础谐波、超谐波和次谐波，其中基础谐波即为一阶谐波，而超谐波和次谐波对应的频率均可以表示为一阶谐波频率的倍数，即倍频。本节将通过建立线性最小二乘方法，识别出飞轮各个方向干扰力或力矩的主要倍频。

定义飞轮倍频特性的线性最小二乘估计的费用函数为：

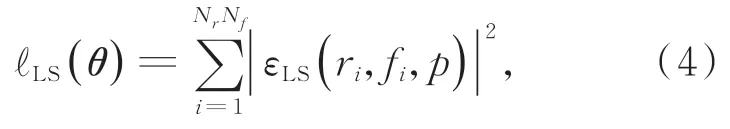
其中：系数p为待估计的倍频系数，ri为第i个转频采样点的转速，fi为第i个转频采样点的频率值，Nr和Nf分别为转速点数和频率点数，误差函数可以表示为：

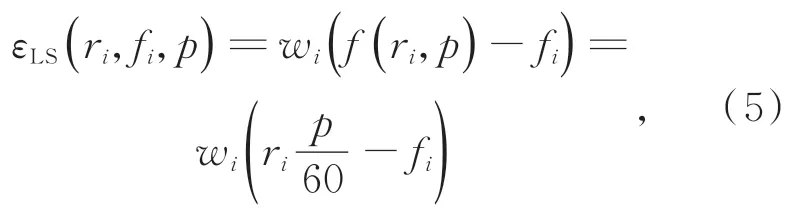
其中：wi为第i个时频采样点的权值，引入一个如图1 所示的扇形窗函数，窗函数可以表示为：

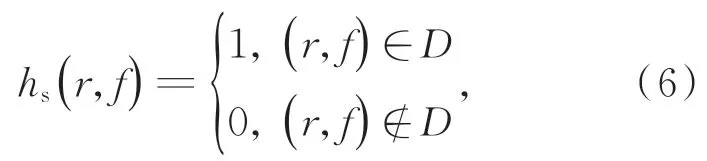
其中D定义了一个域，在域中p1≤r/f＜p2。

将第2.2 节得到的时频分布函数G(r，f)写为向量形式：

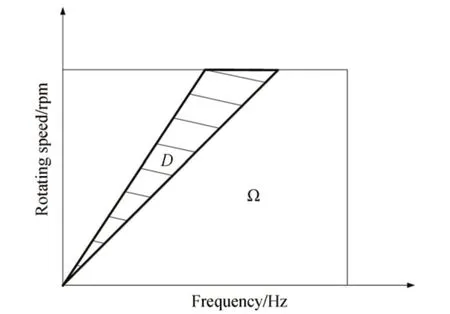
图1 扇形窗Fig.1 Sector window

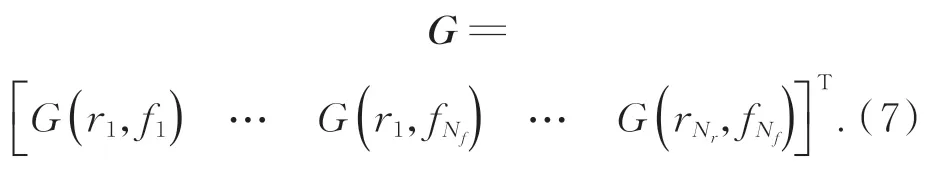
并令权函数wi=hsiGi，则误差函数可以表示为：

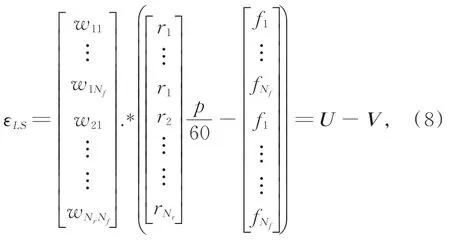
其中：符号.*表示两向量元素相乘，待估参数p的最小二乘解可以表示为

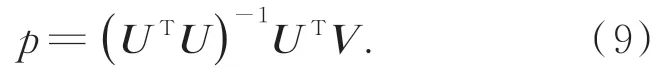
通过改变扇形窗函数的分布，即可识别出不同扇形窗内的倍频特性。

3 反作用飞轮模态参数识别

3.1 参数化的矩阵分式模型建立

本节将建立一种与转速相关的参数化的飞轮结构模态参数识别方法，首先建立飞轮的参数化矩阵分式模型［16］，利用加权非线性最小二乘方法估计出模型的待估参数，最后将矩阵分式模型参数转化为模态参数。

飞轮的动力学模型可以写为如下形式的参数化的右矩阵分式模型：

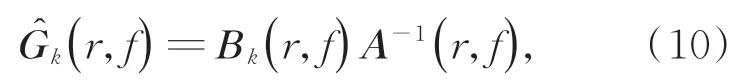
其中：Bk为分子系数矩阵，k表示第k个输出信号，A为分母系数矩阵，r表示转速变量，f表示频率变量。对于单参考情况，可以简化为公分母模型：

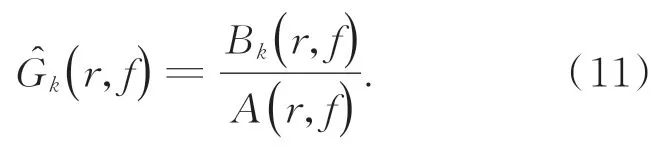
将分母系数和分子系数定义为如式（12）所示的多项式形式：

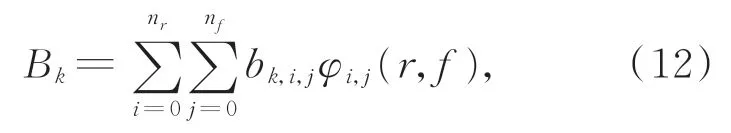
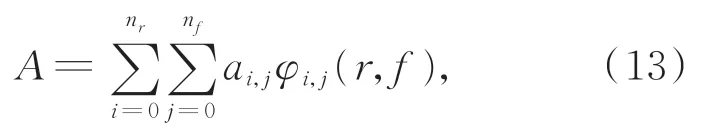
其中：φi，j(r，f)表示与频率和转速相关的基函数，采用正交多项式与z域多项式混合形式φi，j(r，ω) =pi(r)zj，bk，i，j和ai，j为 多 项 式 系 数 ，nr和nf分别为转速多项式和频率多项式的阶数［17］。

将多项式系数写成向量形式如下：

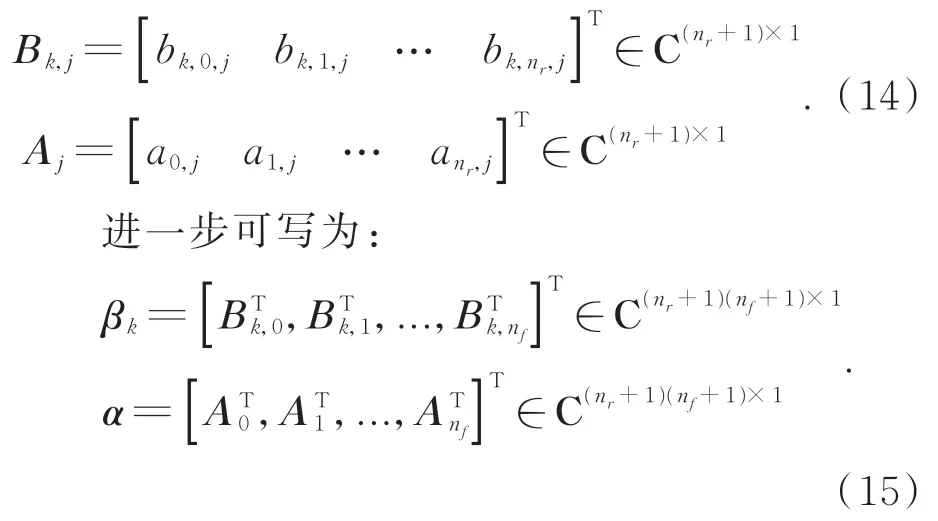
则右矩阵分式模型的所有待估参数写成以下形式：

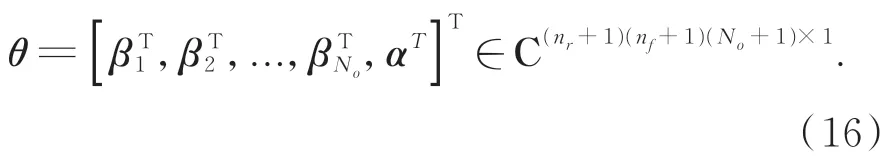
3.2 加权非线性最小二乘法处理

本小节利用加权非线性最小二乘估计方法辨识出参数化模型的待估参数，将模型参数转化为模态参数。加权非线性最小二乘估计的费用函数可以表示为：

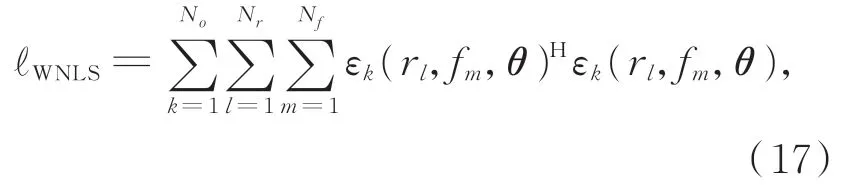
式中，符号H 表示矩阵的共轭转置，第k个输出信号的误差函数εk(rl，fm，θ)可以表示为：

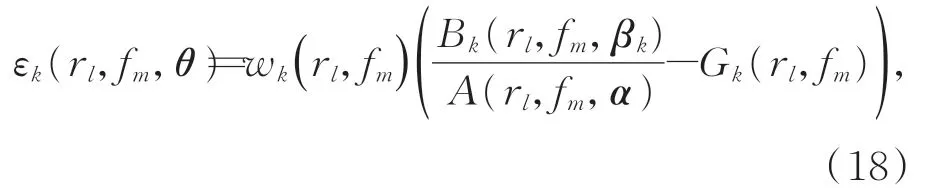
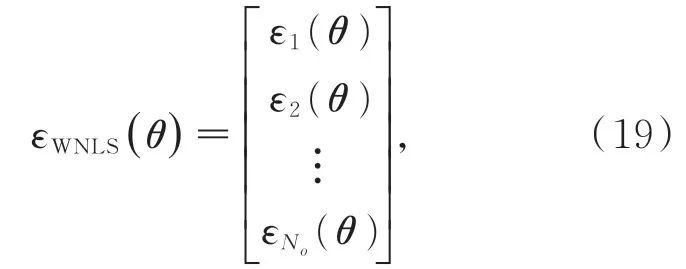
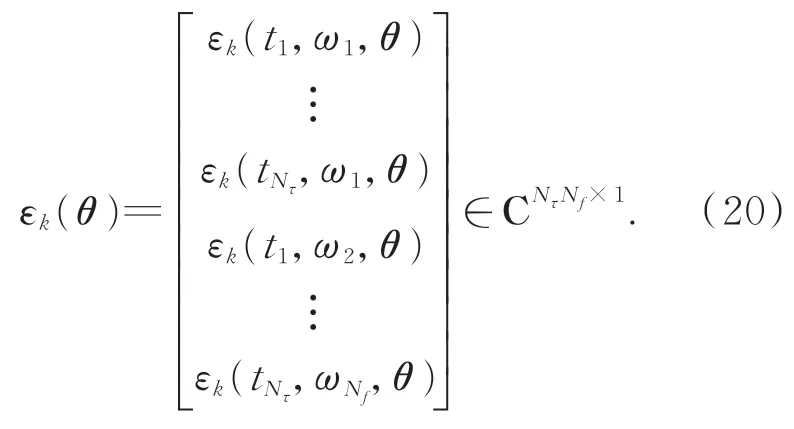
加权非线性最小二乘方法的待估参数θ需要通过迭代的方式计算，采用Gauss-Newton 算法，待估参数θ的增量 Δθ可由如式（21）的线性方程进行求解：

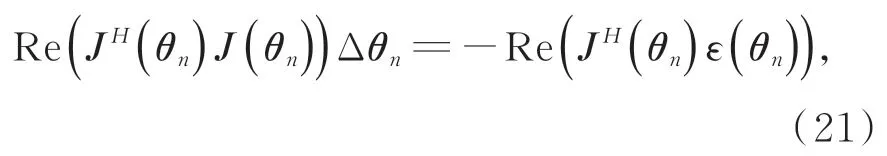
其中：J(θn)表示第n个迭代步的 Jacobi矩阵，Jacobi矩阵J的含义是误差函数对待估参数θ的偏导：

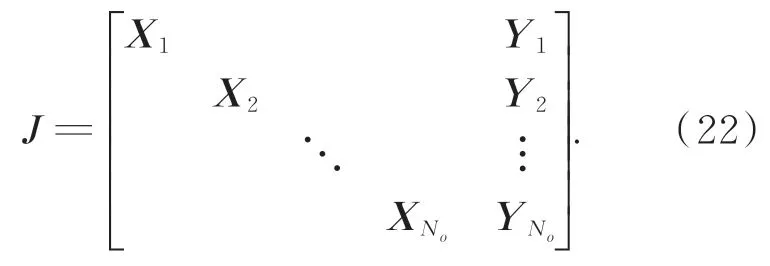
Jacobi 矩阵中对应的分块矩阵如式（23）所示：

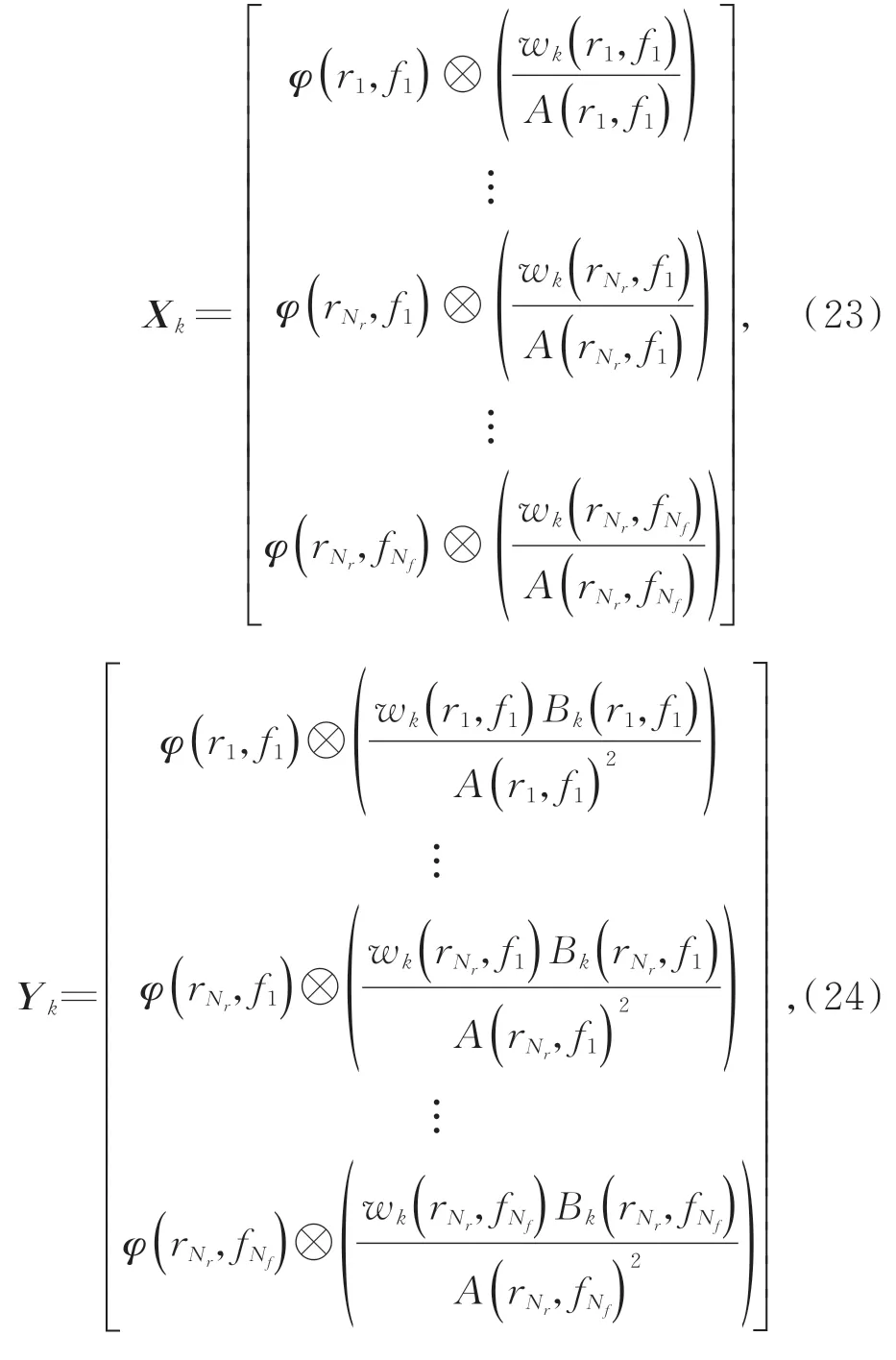
其中⊗表示kronecker 积，

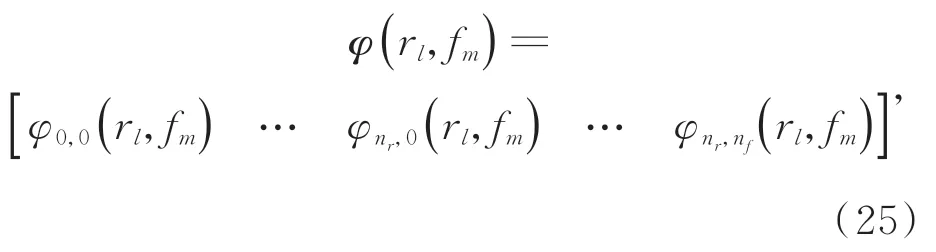
则式（21）可以表示为：

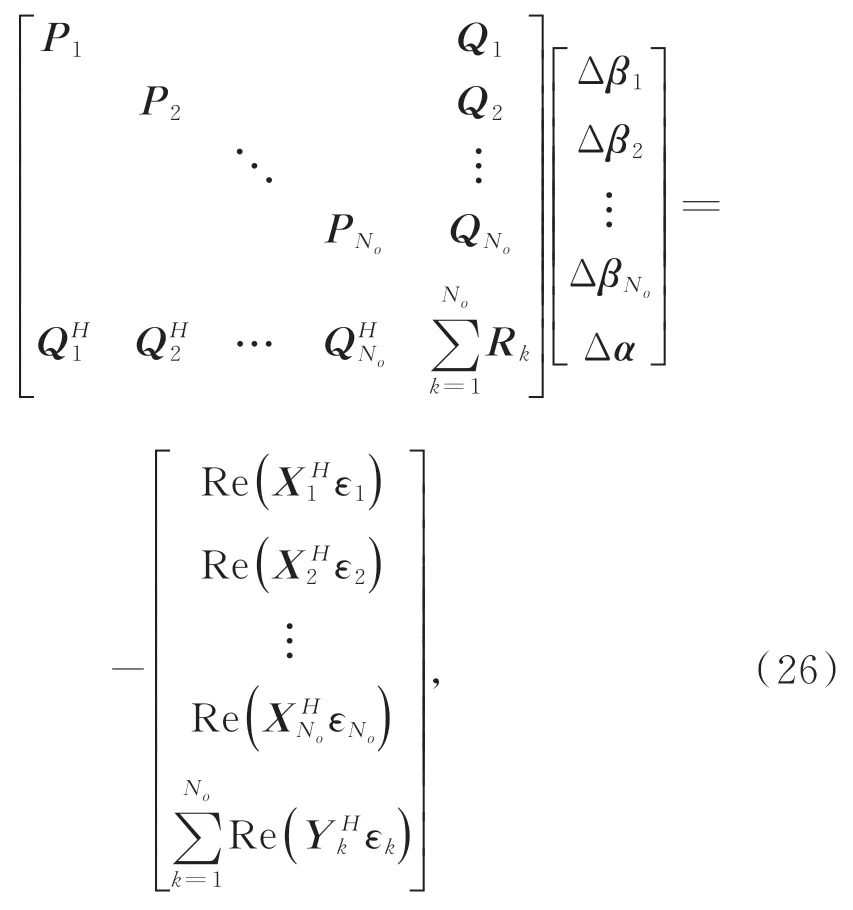
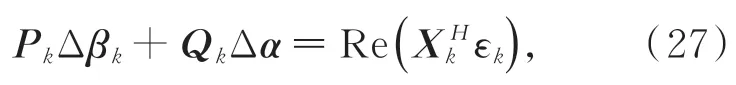
根据式（26）的第No+1 行，可得：

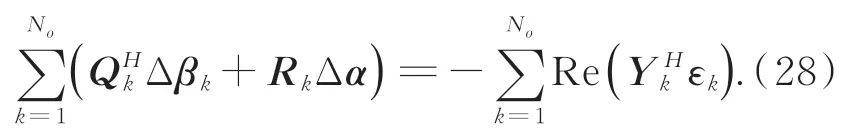
结合式（27）和式（28）消去 Δβk，可得到缩减正则方程如式（29）：

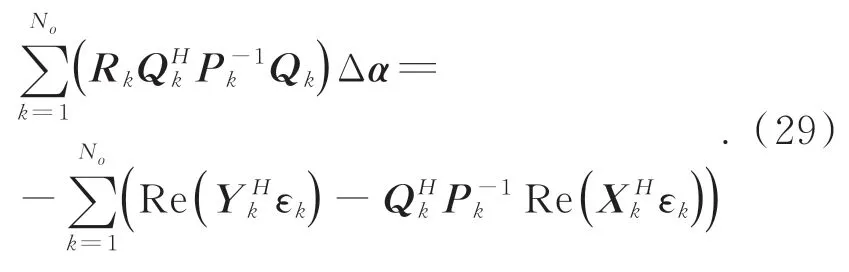
定义矩阵：

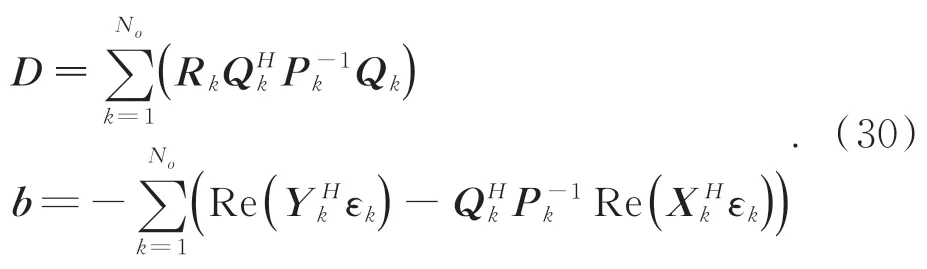
则通过求解式（31）的方程即可得到每一次迭代的 Δα和 Δβk：

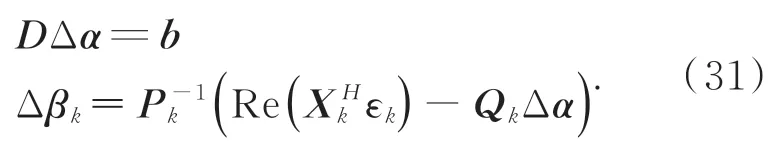
将每步得到的 Δα和 Δβk合写成 Δθ，并对待估参数θ进行更新，即：

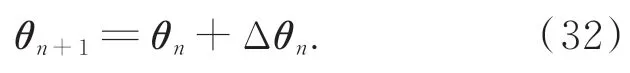
迭代终止条件为：

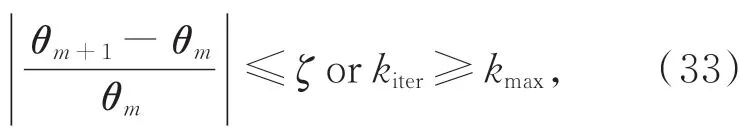
其中：ζ为相对误差的阈值，kiter为迭代次数，kmax为给定的最大迭代次数。

待估参数的初始值θ0可由线性最小二乘估计方法所估计出的参数给定［18］。

3.3 模态参数计算

模态参数可以通过求解如式（34）广义伴随矩阵的特征值获得：

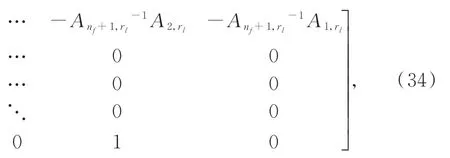
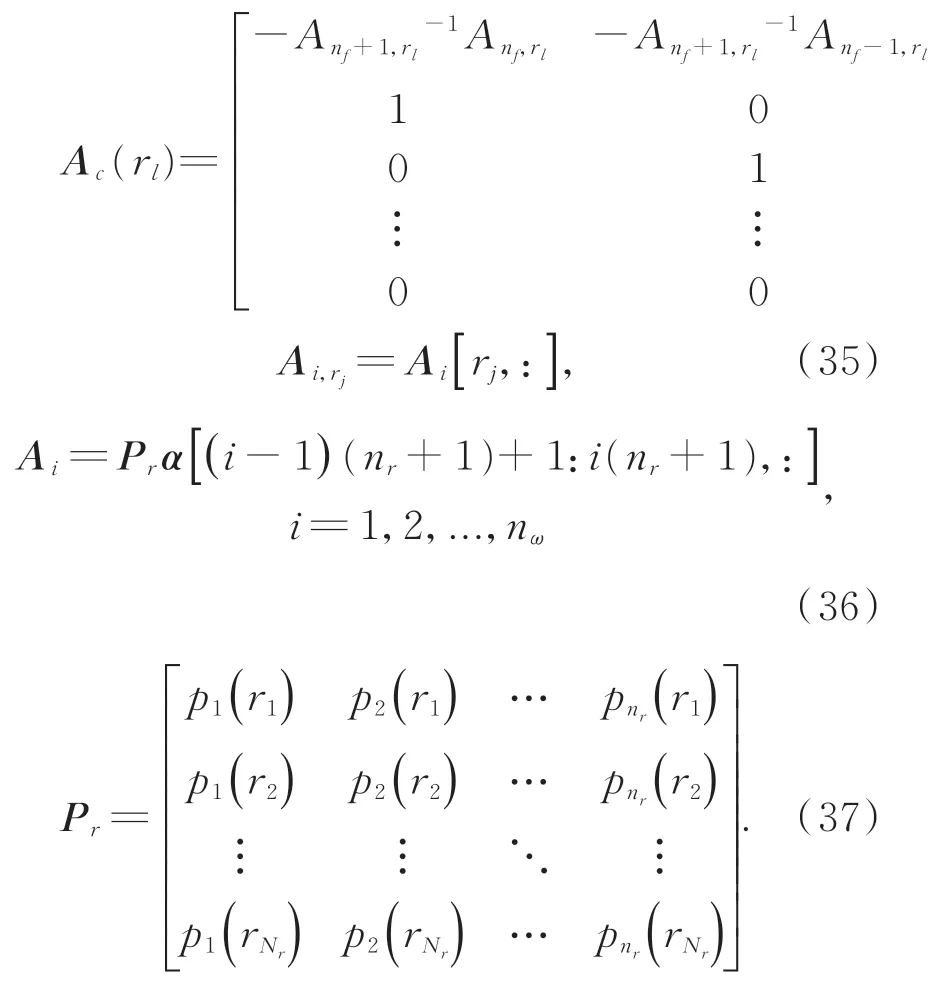
则模态频率fr和阻尼比ξr可以分别表示如式（38）所示：

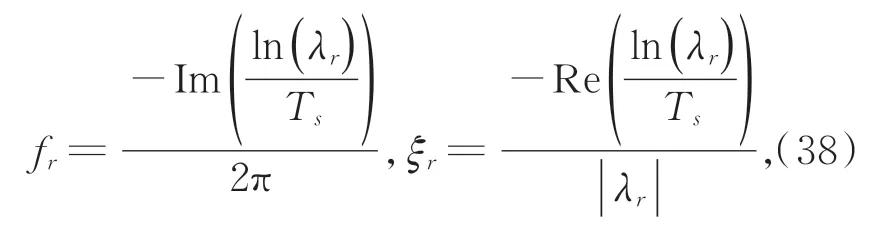
其中：λr为广义伴随矩阵Ac(rj)的特征值，即λr=eig(Ac(rl))。

4 试验与分析

本节将通过连续转速状态下的反作用飞轮干扰力/力矩测试，来验证本文提出的方法。同时增加一组反作用飞轮固定转速下的干扰力/力矩测试，通过传统的傅里叶变换方法进行分析，并与本文所提出方法的结果进行对比。

根据第2 节和第3 节内容，编写分析程序，程序伪代码如图2 所示。

4.1 试验工况

如图3 所示，试验系统由飞轮、kistler 测力台、试验工装、信号采集系统、控制器、电源和计算机组成。将飞轮通过试验工装连接在测力台上，飞轮方向如图4 所示定义。设定飞轮力矩为0.5 N·m，测试飞轮转速从0 转匀加速转到2 000转的过程，在测得干扰力信号的同时，记录飞轮转速随时间变化的曲线。测试的现场图如图5所示。

试验得到的飞轮的转速时间历程曲线如图6所示，飞轮各个方向干扰力/力矩的时间历程曲线如图7 所示。可以发现，连续转速状态下飞轮的干扰力信号是一条幅值呈上升趋势的非稳态信号。此时利用传统的傅里叶变换方法进行分析时，干扰力在频域上的频率和幅值都将是不稳定的，因此需要将连续转速的干扰力信号转化的时频域上进行分析。

4.2 干扰力/力矩时频分析

利用第2.2 节的方法将干扰力信号转化到时频域，得到干扰力和力矩的转频谱如图8 所示。图中可以发现明显的飞轮结构模态和倍频特性，可以通过本文建立的方法进行识别。

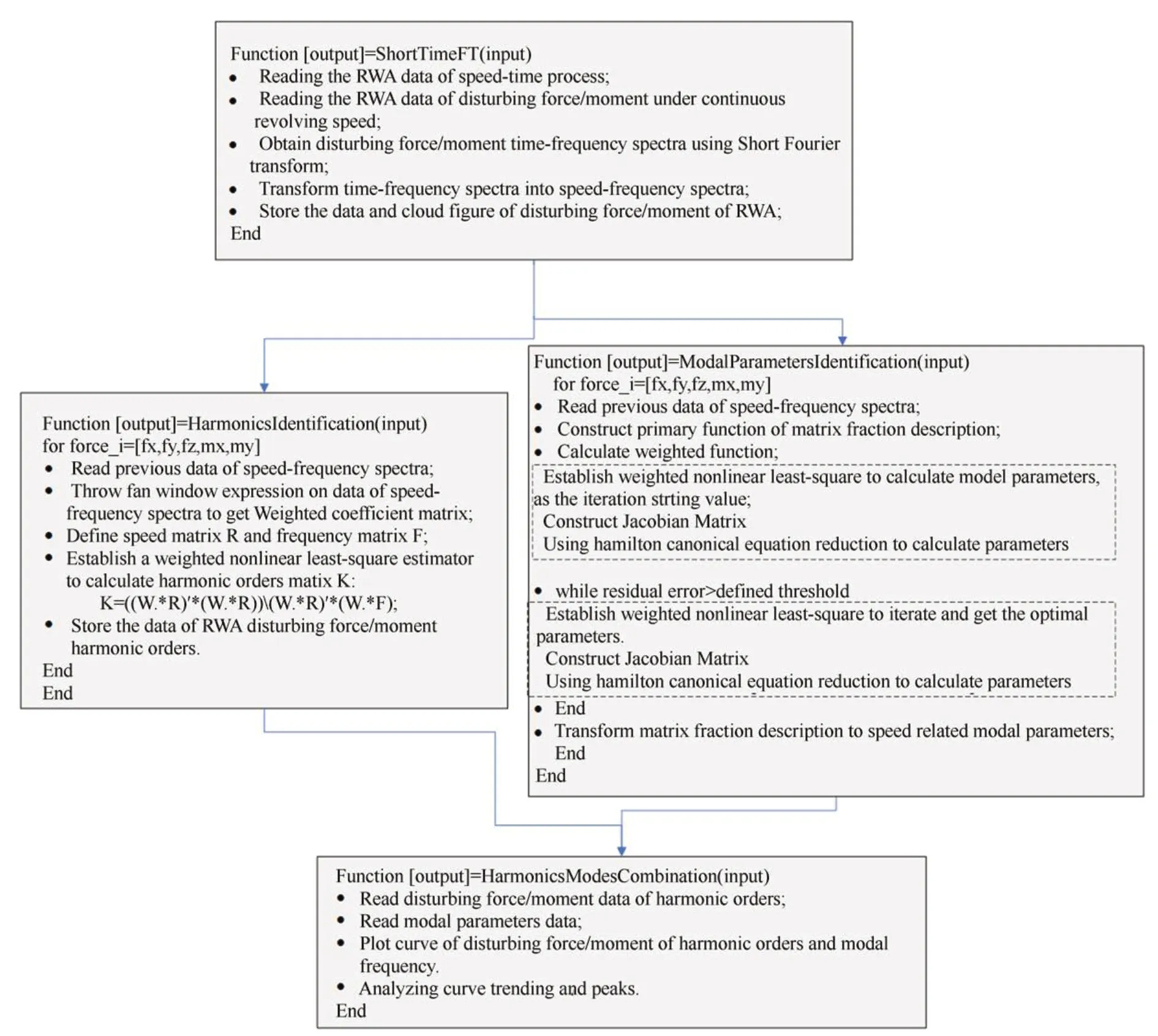
图2 分析程序伪代码Fig.2 Pseudo-code of analysis program

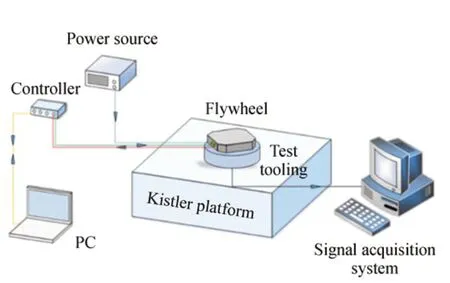
图3 试验系统示意图Fig.3 Schematic diagram of experimental system

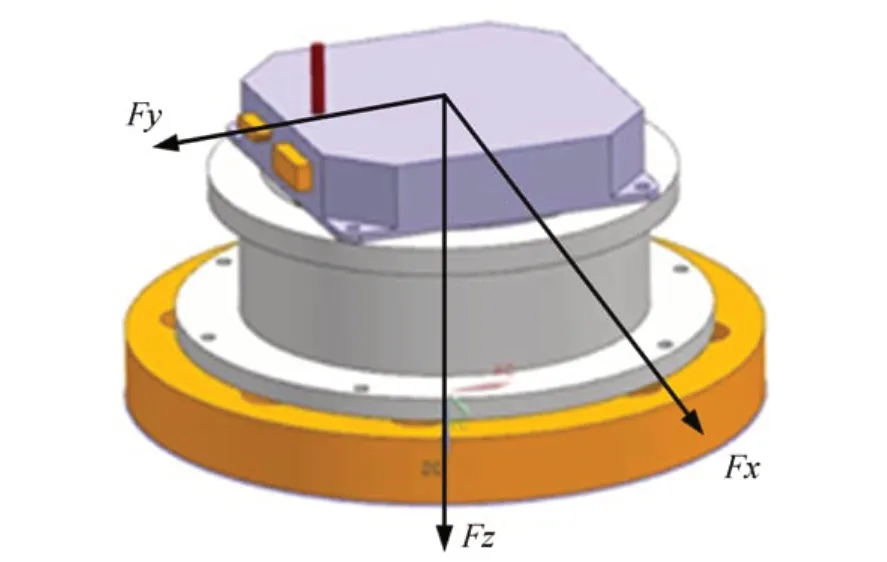
图4 飞轮安装方向坐标定义Fig.4 Flywheel installation direction definition

图5 测试现场图Fig.5 Photo of experimental site

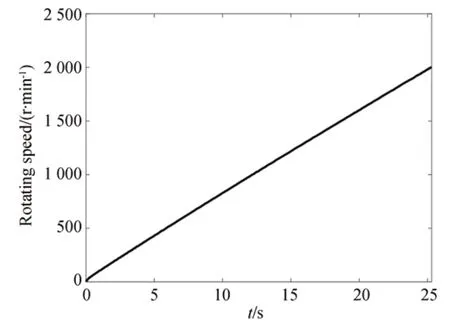
图6 转速时间历程曲线Fig.6 Time history of rotating speed

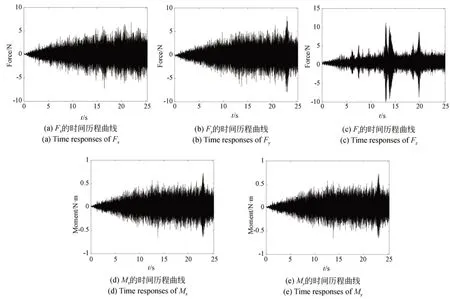
图7 干扰力和力矩信号的时间历程曲线Fig.7 Time responses of the disturbing forces/moments signals

4.3 倍频特性识别

利用第2.3 节建立的方法对飞轮倍频特性进行识别，识别出的各方向干扰力或力矩的倍频特性进行统计如表1 和图9 所示。

4.4 飞轮模态参数识别

利用第3 节建立的方法辨识飞轮的模态参数，设置转速多项式参数nr= 1，频率多项式参数，最大迭代次数kmax= 10，辨识出的转频谱如图10 所示。辨识的随转速变化的模态频率和阻尼比如图11 所示，图中，红色矩形符号表示飞轮的轴向平动模态，绿色圆形符号表示飞轮的摇摆模态，蓝色菱形符号表示飞轮的径向平动模态（彩图见期刊电子版）。所辨识出的飞轮模态可以为飞轮的仿真分析、模型校核以及飞轮系统隔振设计等提供参考。

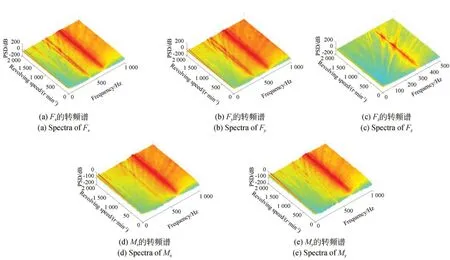
图8 干扰力和力矩的转频谱Fig.8 Speed-frequency spectra of forces and moments

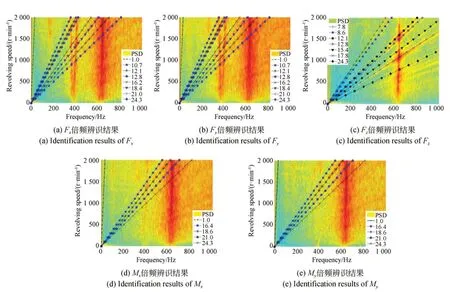
图9 倍频辨识结果（各直线表示各倍频辨识结果）Fig.9 Identification results of harmonic characteristics（Lines denote the identification results）

表1 飞轮各方向干扰力/力矩倍频统计Tab.1 Summary of main harmonic factors

图10 参数化估计的转频谱Fig.10 Parametric estimated speed-frequency spectra

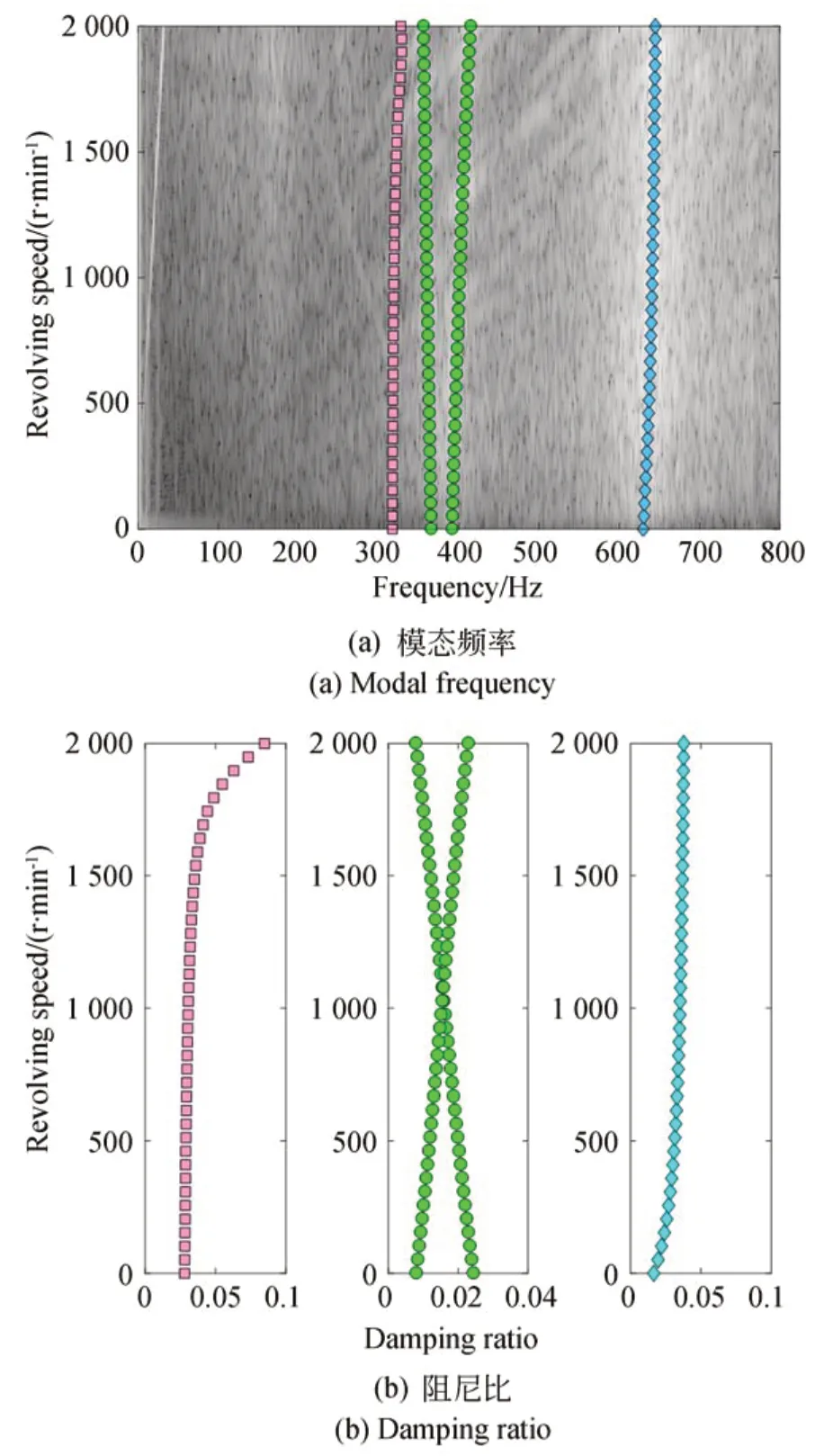
图11 模态频率和阻尼比Fig. 11 Modal frequency and damping ratio

4.5 固定转速试验结果

在进行变转速飞轮干扰力测试的同时，进行固定转速的干扰力测试作为对比试验。从0 转到2 000 转每隔100 转进行一组测试，共进行21 组试验。通过傅里叶变换，得到飞轮的干扰力/力矩随频率和转速变化的瀑布图如图12 所示。

通过结合飞轮模态频率和倍频特性，可以预测干扰力或力矩的峰值点位置。如图13 所示（彩图见期刊电子版），将飞轮轴向模态频率和倍频曲线显示在同一张图上，两曲线交点即为干扰力转频峰值点。通过表2 给出了连续转速试验和固定转速试验的轴向干扰力的转频峰值点及其相对误差，可以发现两种方式得到的峰值点误差最大为4.3%，平均误差经计算小于1%。并且固定转速试验得到的峰值点只能出现在试验测试设定的转速上，容易忽略最大峰值点所出现的转速。而连续转速方法可以得到干扰力（或力矩）的平滑变化趋势。此外，连续转速试验的试验量仅为固定转速试验的4.8%。

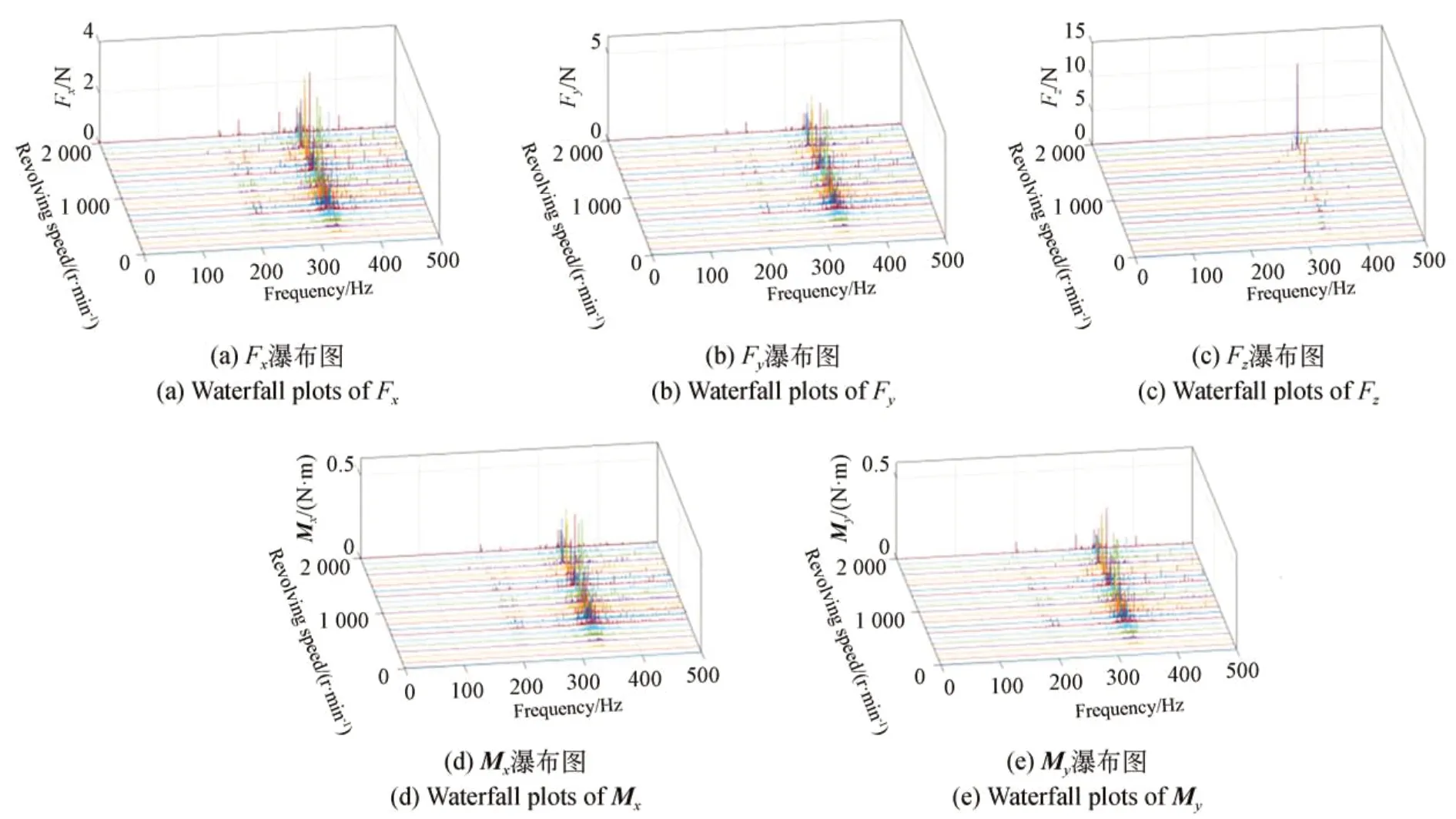
图12 固定转速试验瀑布图Fig.12 Waterfall plots of the fixed-speed tests

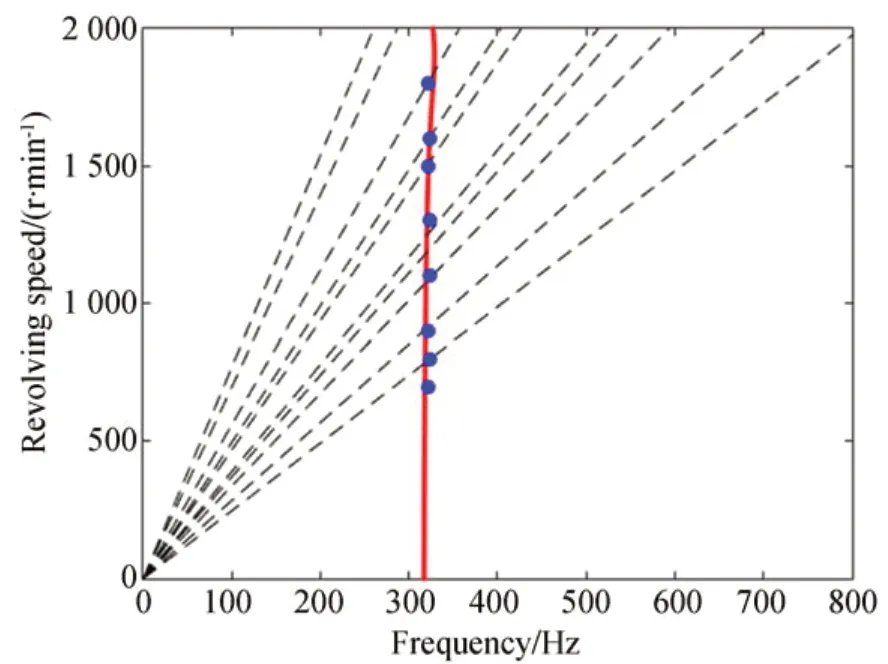
图13 轴向干扰力峰值分布（红色实线表示模态频率，黑色虚线表示倍频曲线，蓝色点表示参考试验的峰值点）Fig.13 Distribution map of the peak points of Fz（red line denotes modal frequencies，black dash lines are the harmonic frequencies，blue points denote the peak points）

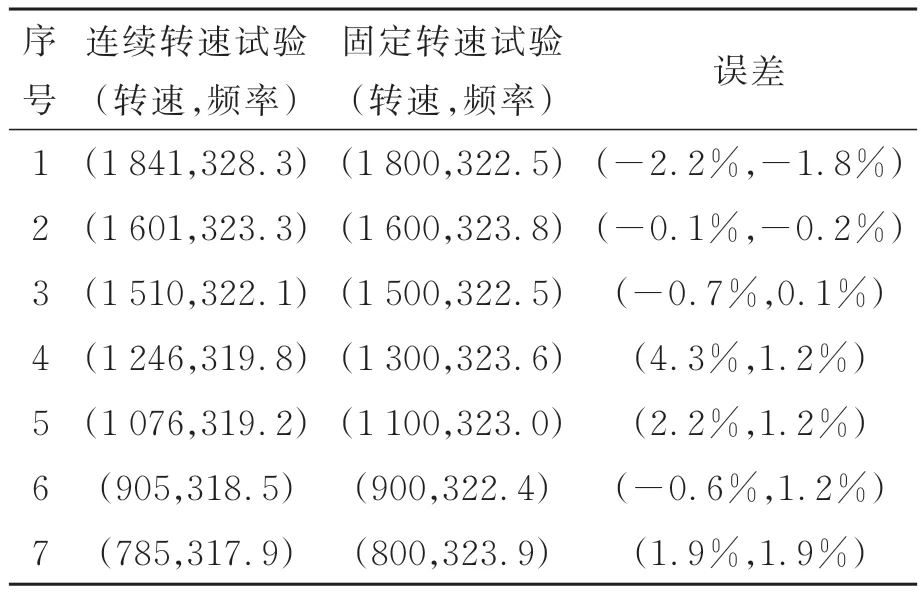
表2 轴向干扰力的转频峰值点Tab.2 Speed-frequency points of peaks of Fz

5 结 论

本文建立了一种连续转速下反作用飞轮的参数识别方法，该方法利用连续转速干扰力数据，识别出飞轮的模态参数和倍频特性，所识别的结果相对于固定转速参考试验的结果基本一致，但是却获得了固定转速测试所不能得到的干扰力（力矩）平滑变化趋势数据，对飞轮扰振特性有更准确地了解。通过结合倍频特性和模态频率特性，可以计算出飞轮干扰力和力矩的转频峰值点。本文提出的方法提高了飞轮参数辨识的效率，揭示了飞轮干扰力/力矩随转速变化的关系，可以用于反作用飞轮特性的获取，识别的模态频率、阻尼比、倍频以及转频峰值点等特性，可以为后续飞轮模型校核、仿真分析以及整星微振动分析与试验等微振动相关技术的研究提供参考。