双星编队构形保持抗干扰容错控制
2021-04-22陈高杰杨秀彬杨春雷黎艳博
陈高杰 ,常 琳 ,杨秀彬 ,杨春雷 ,黎艳博
(1. 中国科学院长春光学精密机械与物理研究所,吉林长春130033;2. 中国科学院大学,北京 100049;3. 中国科学院天基动态快速光学成像技术重点实验室,吉林长春130033)
1 引 言
卫星编队凭借其可靠性高、灵活性强、适应性广的特点,拥有极高的应用价值,已经被广泛应用于科学实验、近地观测、深空探测、干涉测量等诸多领域[1-4]。卫星工作于真空失重状态,长期受到强辐射及高低温等恶劣空间环境的影响,并且卫星自身元器件工艺水平、老化磨损均会导致执行器发生故障。若卫星发射入轨后发生故障,一般难以修复,需要使用星上冗余元器件保证卫星继续工作。但受到卫星研发和发射成本的限制,难以在卫星系统上安装过多元器件,另外,卫星运行过程中,受到地球质量分布不均和非球形、日月三体引力、大气阻力、太阳光压等影响,导致编队构形发生变化,故需设计合理的故障估计以及容错控制策略,进行构形保持控制,以提高卫星编队系统的可靠性和安全性[5]。
针对故障估计与容错控制,众多学者进行了大量研究,其中一些方法已广泛应用于卫星编队轨道控制系统[6-8]、航天器姿态控制系统[9-11]、无人机飞行控制系统[12-13]及电力电子控制系统[14-15]等领域。文献[6]为解决碰撞避免、障碍规避的问题,设计了结合势函数制导方法的滑模协同控制策略,同时在所提控制算法中引入自适应律,提高了执行器故障容错控制、参数自适应能力,使航天器编队在进行目标跟踪和构形保持的同时,防止编队航天器间碰撞并具备躲避障碍物的能力。文献[16]基于H∞最优理论和矩阵奇异值分解技术,使用分散状态反馈方法,对卫星轨道保持系统进行容错控制研究,提出了允许执行器故障和传感器故障的两种分散控制方法,在保持故障系统渐近稳定的同时,使控制性能在H∞范数意义下达到次优。文献[17]设计了非线性增广观测器,此观测器考虑多种故障形式,而不局限于常值或缓变故障,进一步针对一般情况下的系统,设计了鲁棒增广观测器,可以进行更精确的故障估计,且适用于多个故障并发情况。文献[18]针对推进器堵塞或关闭等故障情况,提出基于H∞/H-的滤波器的故障估计方案,仿真表明,该滤波器在航天器存在测量噪声、测量延迟、传感器失调的情况下,能够进行故障的精确诊断,并隔离故障。文献[19]通过故障辨识模块和辅助系统模块进行故障估计,通过反步容错控制方法,使编队存在拓扑故障、舵面故障、执行器故障和不确定性的情况下,依然可以使编队稳定飞行。另外,编队卫星长期在轨运行,可能发生故障的同时,亦会受到多种内部或外部摄动干扰的作用,这些干扰均会严重影响编队卫星正常轨道运动,导致卫星编队实际构形偏离预设构形[20]。然而,少有文献综合考虑包括模型误差、卫星故障以及外部干扰等在内的安全问题,并且当此类飞行要求与设计的构形保持控制目标相结合时,将进一步增加控制器的设计难度[6,17]。
故本文在对卫星编队系统进行故障估计的基础上,考虑未知扰动及系统模型参数不确定性,对卫星编队进行抗干扰容错控制研究。首先设计可以综合估计系统模型误差、外部干扰以及执行器故障的观测器系统,对系统未知信息进行估计,另外在观测器设计时,加入残差微分模块,提高估计准确度。然后基于相关估计信息,引入H∞方法,减弱不可建模干扰部分对系统的影响,设计闭环反馈抗干扰容错LQR 控制策略。最后仿真结果表明,所提基于观测器的控制策略具有更精确的控制性能。
2 卫星编队动力学模型
2.1 坐标系定义
2.1.1 地心赤道坐标系(惯性坐标系)Oe-XiYiZi
坐标系原点Oe为地心,以赤道面作为基准面,Xi轴指向春分点,Yi轴在轨道面内由Xi轴向东转90°,Zi轴垂直赤道面指向北极。
2.1.2 参考星质心轨道坐标系(相对运动坐标系)O-XoYoZo
坐标原点O位于参考星质心,Xo轴与参考星地心矢量rm重合,Yo轴在参考星轨道面内垂直于Xo轴并以指向参考星运动方向为正向,Zo轴和Xo,Yo轴构成右手系。坐标系示意图见图1。
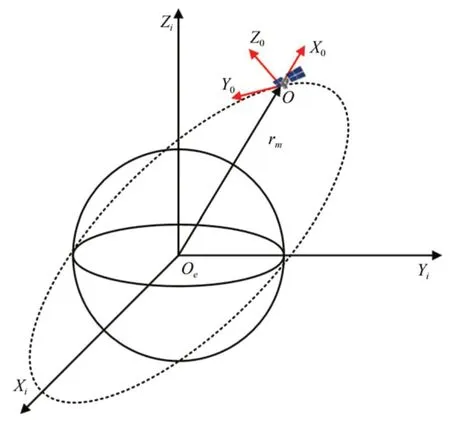
图1 坐标系示意图Fig.1 Coordinate system schematic diagram
2.2 相对运动动力学模型
双星编队由参考星和跟随星组成,两星沿飞行方向相隔一段距离,以设计构形运行于同一太阳同步轨道上。假设卫星运动轨道为圆轨道,将两颗卫星均视为质点,采用经典C-W 方程相对运动动力学模型[21]表示:
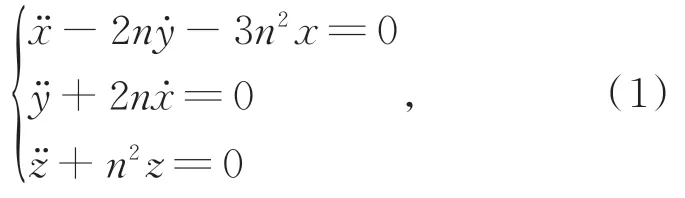
其中:x,y,z分别为两星相对距离沿X轴,Y轴,Z轴分量,n为参考星轨道角速率。
考虑对编队卫星进行控制的情况,相对运动方程组(1)可转化为方程组(2):

其中,μx,μy,μz分别为控制力在轨道坐标系下的 3个坐标轴分量。
由式(2)可得系统状态空间方程:

其中:状态变量χT(t)=[x y z x˙y˙z˙]T表示三轴相对位置和速度,输出变量ζT(t)=[x y z]T表示传感器测量值;A,B,C矩阵取:
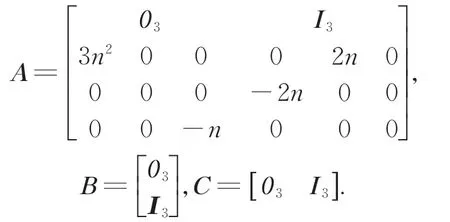
此外,考虑参数摄动、外部扰动、执行器故障等模型不确定因素,则双星编队控制系统可描述为:
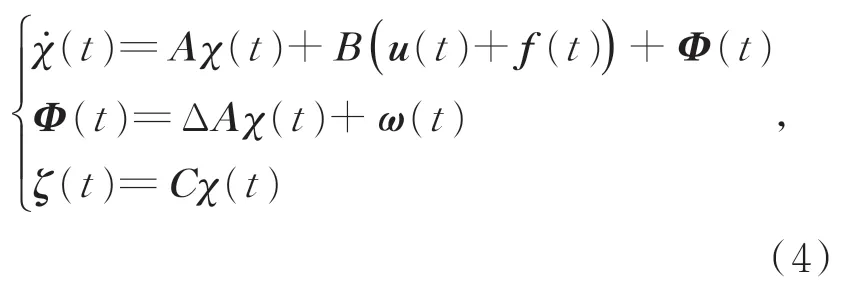
其中:f(t)表示执行器故障;ω(t)表示外部扰动变量,如空间干扰力;Φ(t)表示因参数摄动、外部扰动等引起的等效未知干扰向量;ΔA表示由地球质量分布不均和非球形、日月三体引力、大气阻力、太阳光压等参数不确定导致的摄动矩阵,且满足ΔAχ(t)=Dd1(t)+Δ,其中D表示具有参数摄动结构信息的已知矩阵,d1(t)和Δ 分别表示具有参数摄动能量信息的可建模干扰与不可建模干扰。
基于上述模型,给出以下假设:
假设1.故障范数有界且可微,满足‖f(t) ‖≤η1,其中η1与η2为有界正实数。
假设2. 外部干扰具有如下形式:
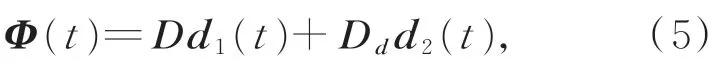
其中:Ddd2(t)= Δ+ω(t),Dd表示干扰分布矩阵,d2(t)表示不可建模干扰,如随机噪声、模型不确定性。假设d2(t)是范数有界的,同时,可建模干扰d1(t)可等效为以下外系统的输出:
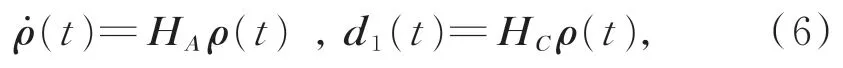
其中:ρ(t)表示外系统的状态,HA和HC是具有适当维数的已知矩阵。
假设3. 系统(4)能控且能观。
系统(4)可转化为如式(7)的形式:
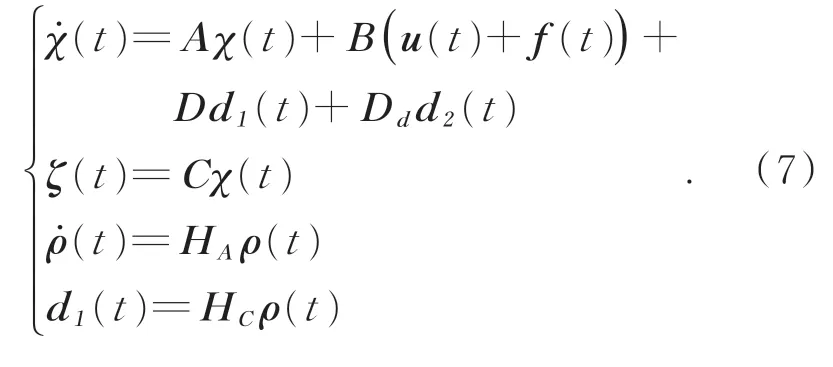
3 观测器设计
本节主要给出自适应观测器的设计方法及存在条件,进行稳定性与鲁棒性分析,同时给出其证明过程,以及求解观测器设计参数的LMI(线性矩阵不等式)算法。
3.1 自适应观测器设计
基于系统(7),设计如式(8)所示的自适应观测器:

其中:L为观测器增益,F1与F2为故障估计权重,G1与G2为干扰估计权重,以上均为待设计参数变量表示估计状态表示估计输出,表示估计故障表示外系统(6)估计状态。
定义如下变量:
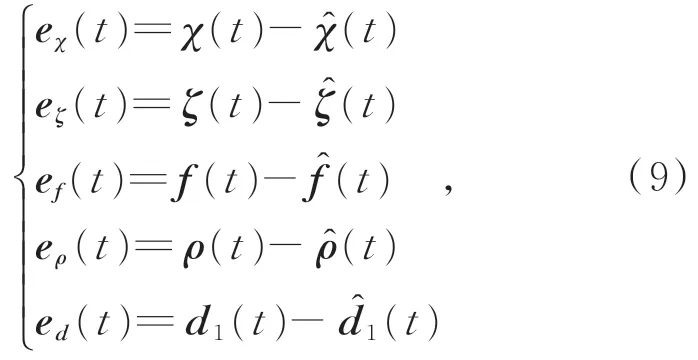
其中:eχ(t)表示状态估计误差,eζ(t)表示输出残差,ef(t)表示故障估计误差,eρ(t)表示外系统(6)状态估计误差,ed(t)表示干扰估计误差。
由系统(7)和观测器系统(8),可以得到动态误差系统:
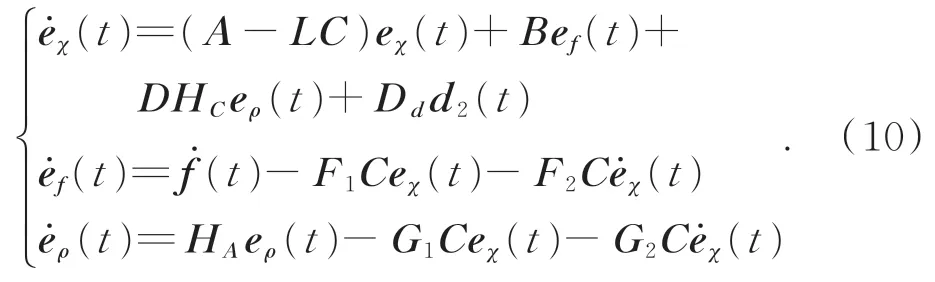
将系统(10)增广为如式(11)的形式:

对于任何F2C和G2C,均为非奇异矩阵,则系统(11)可转化为:
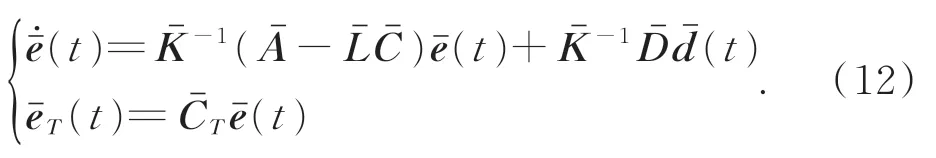
对系统进行Laplace 变换,可以得到系统动态误差:表示估计干扰
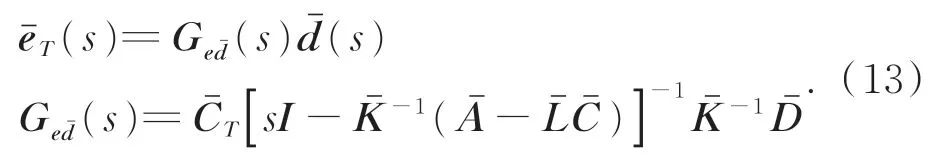
注1.对系统(8)中的自适应律进行积分,有:
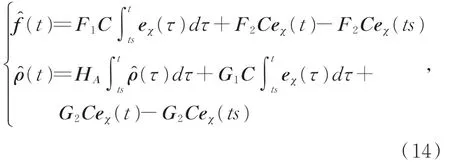
其中:ts为系统未发生故障时的某一时刻,在不考虑外扰等条件下有eχ(ts)=0。此时故障估计器与干扰估计器均包含比例与积分两个模块,相较于常规的自适应算法,增加的比例单元,一方面增加了算法设计的自由度,另一方面也能有效提高故障与干扰估计的快速性和精度,这在后文仿真对比实验中得到验证。
首先给出本文要用到的一些引理。
引理1. 存在对称正定矩阵P使得对满足βTβ≤υTCTCυ的所有υ≠ 0 和β,有:
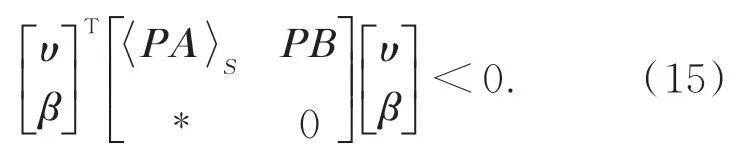
成立当且仅当存在标量τ,使得:

其中:符号A S表示A+AT,*表示该矩阵的对称元素。
引理2. 给定矩阵A,A的全部特征值均位于圆形稳定域C(c,r),其中c与r分别为圆形稳定域的圆心与半径,当且仅当存在正定对称矩阵P,使得:

3.2 稳定性与鲁棒性分析
为设计观测器增益矩阵L,权重矩阵F1,F2,G1,G2使所提鲁棒自适应观测器能够快速精确地系统模型误差、外部干扰以及执行器故障,给出如下定理。
定理1. 考虑系统(7)、观测器系统(8),如果存在观测器增益L,故障估计权重F1与F2,干扰估计权重G1与G2,常数α> 0,ε> 0,当且仅当存在对称正定矩阵P,矩阵Y,使得:
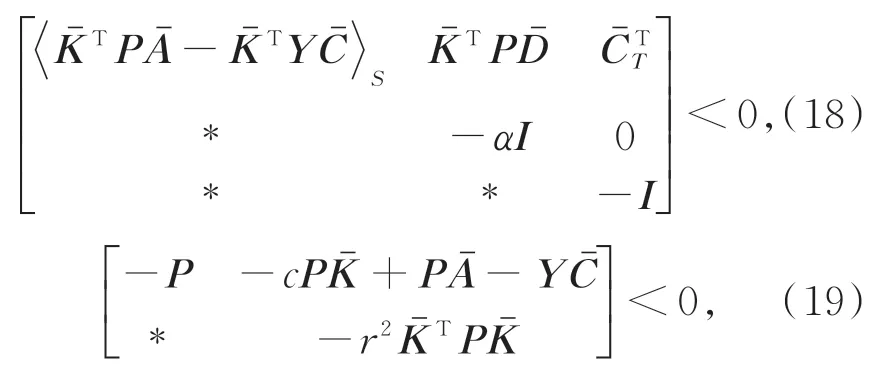
证明:由于是非奇异的,对于对称正定矩阵P而言,易知矩阵也一定是对称正定的。可选取Lyapunov 函数为:
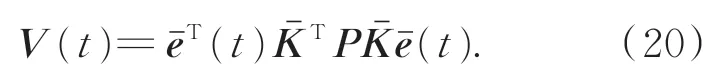
显然,V(t)是正定的。首先,讨论当=0时系统(12)的稳定性问题。求式(20)对时间的导数,有:
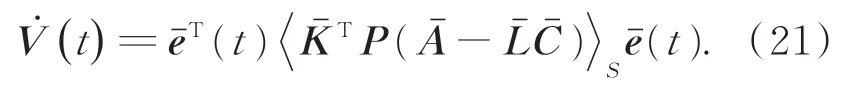
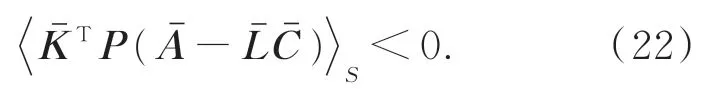
当式(22)满足时,系统(12)是渐近稳定的,状态估计误差eχ(t),故障估计误差ef(t)和干扰估计误差ed(t)渐近收敛于0。
参考H∞性能指标,有:
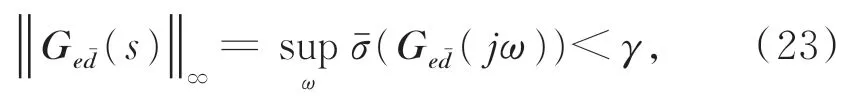
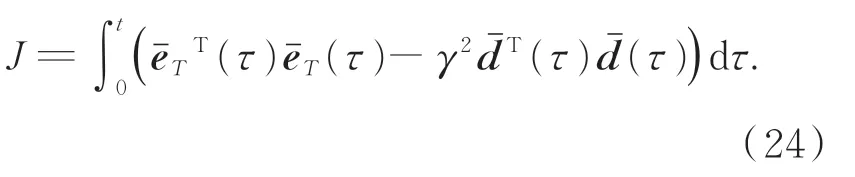
则在零初始条件下,有:

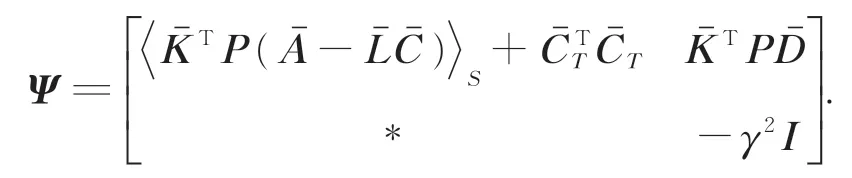

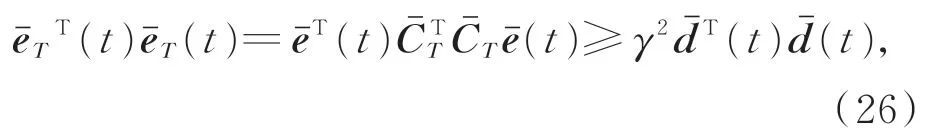
能够保证式(27)的成立:
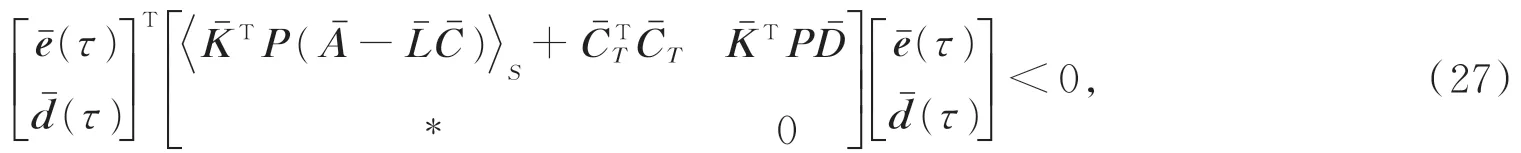
且存在T> 0,对于任意t>t0+T,有:
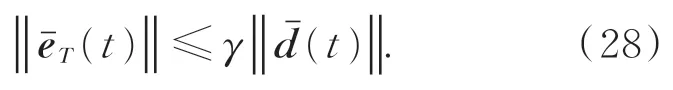
这表示动态误差系统是渐近稳定的,且系统状态、故障、干扰的估计误差eˉT(t)最终一致有界。
由 Schur 补引理,式(25)可转化为如式(29)等价形式:
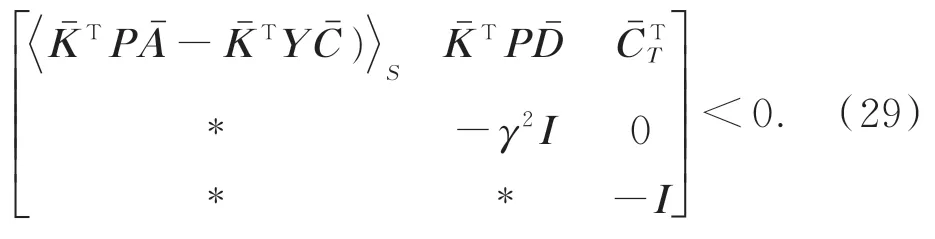
其中条件(29)的满足隐式地保证了条件(22)也成立。
给定圆稳定域C(c,r),由引理 2,存在对称正定矩阵有:
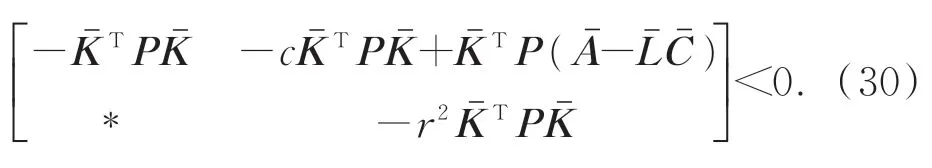
对式做合同变换,得到:
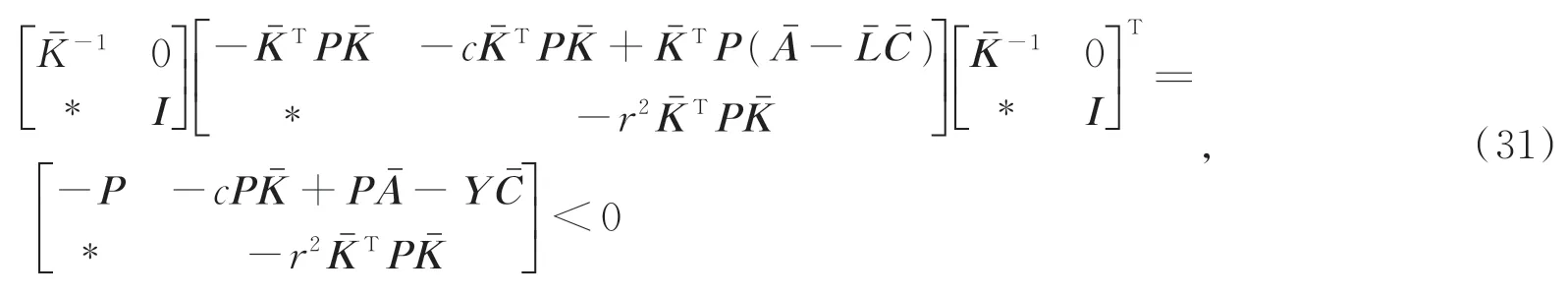
得证。
4 抗干扰容错反馈控制策略
针对卫星编队构形保持控制系统,常用的控制方法主要有:LQR(Linear Quadratic Regulator)最优控制、滑模变结构控制、李雅普诺夫控制等方法。其中,LQR 最优控制形式简洁,方便设计而且物理意义明确,因此本文采用LQR 方法进行卫星编队构形保持容错控制,并结合故障估计、干扰补偿项来减小控制误差,提高控制精确度,控制系统结构图见图2。
二次型指标最优性能指标函数如式(32)所示:
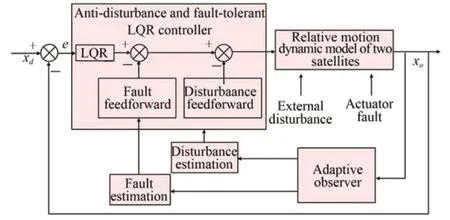
图2 闭环控制框图Fig.2 Close-loop of satellite formation control system
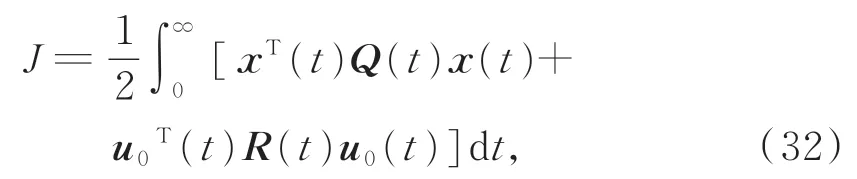
其中:Q为半正定对称矩阵,表示状态x权重,影响控制过程中响应速度,R为对称正定矩阵,对控制能力的要求,决定控制过程中能量消耗,u0为控制输入。
根据最优控制理论,反馈控制律是:

其中K为最优反馈矩阵,求解Riccati 微分方程:
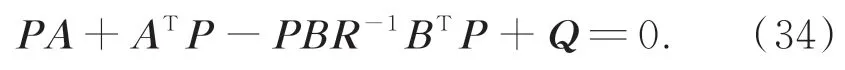
得最优矩阵反馈矩阵K:

其中,P为Riccati 微分方程的唯一解。
设计如下基于观测器的动态输出前馈补偿容错抗干扰控制器:
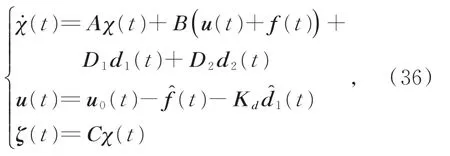
其中,Kd由式(37)给定:
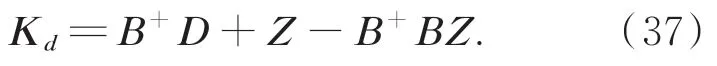
满足BKd=D,其中Z是适当维数的任意矩阵,B+表示矩阵的Moor-Penrose 逆矩阵。
5 仿真实验分析
为了验证本文所提方法在双星编队构形保持控制的有效性,本节进行仿真分析。为便于分析,假设参考星、跟随运行于圆轨道,进行协同遥感拼接成像任务,相较于单星遥感成像方式,双星拼接宽幅成像方式使用多颗卫星对相邻区域进行观测,使用图像拼接技术,可以获得超宽幅图像。使用LQR 控制器进行精确相对位置控制,使双星编队从初始构形恢复至期望构形。
极点配置取O(-30,29),由定理 1 得到观测器设计参数:观测器增益矩阵L取:

故障估计权重矩阵F1与F2取:

干扰估计权重矩阵G1与G2取:
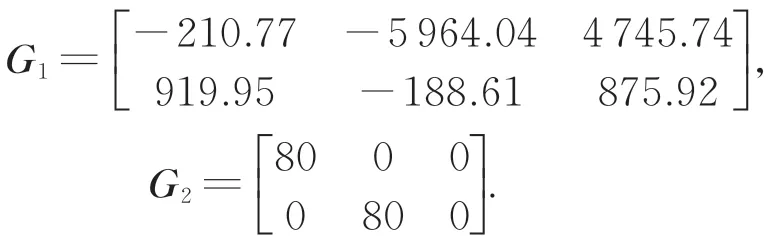
假设卫星编队系统在轨飞行过程中,受到的外部干扰d1(t)、d2(t)影响,其中,d1(t)为可建模干扰,d2(t)∈ [-1,1],表示在 0~20 s 区间内的随机干扰。假设干扰的分布矩阵为:

外部干扰系统(6)参数矩阵:
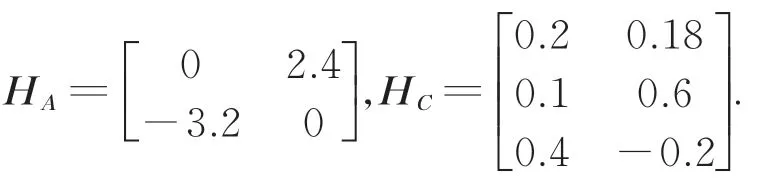
执行器故障设计如下,同时考虑了无故障(x轴)、间歇性故障(y轴)、时变故障(z轴)三种情况:
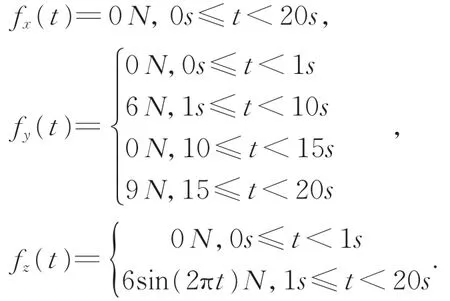
其他相关参数选取见表1。

表1 控制器仿真参数设置Tab.1 Controller simulation parameters setting
根据上述条件,仿真结果如图3~图5。
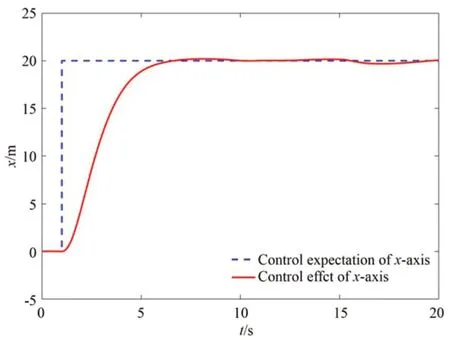
图3 x 轴控制效果Fig.3 x-axis control effect
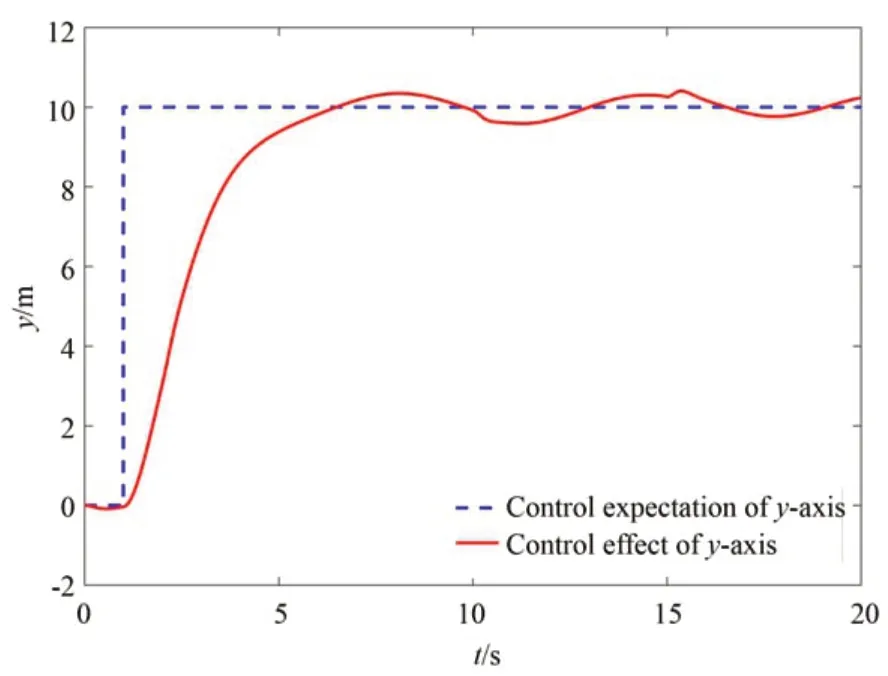
图4 y 轴控制效果Fig.4 y-axis control effect
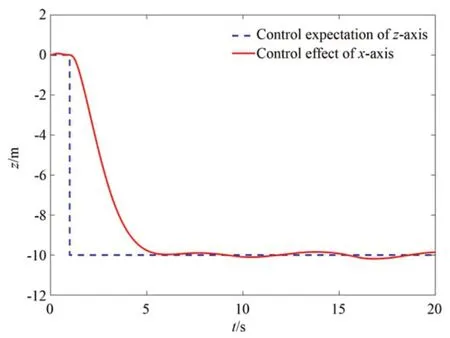
图5 z 轴控制效果Fig.5 z-axis control effect
图3~图5 表示控制效果,从图中可以看出,在存在系统模型误差、外部干扰以及执行器故障的等复杂太空环境下,使用本文提出的基于观测器的容错控制方法,可以快速使编队恢复预设构形,并在较短的时间内使系统达到稳态,且构形恢复过程较为平稳,震荡较小且几乎没有波动。
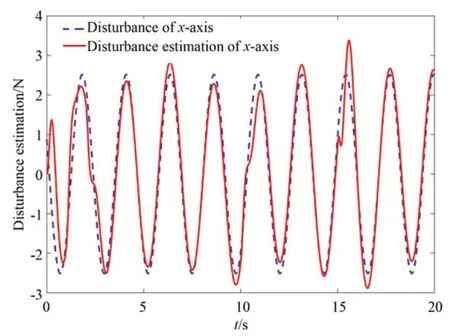
图6 x 轴干扰估计Fig.6 x-axis disturbance estimation
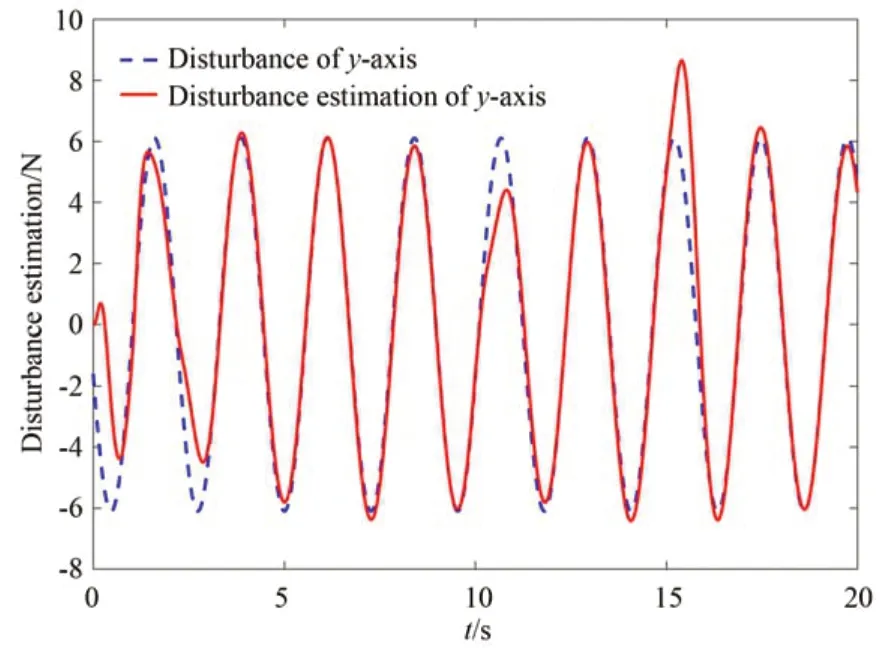
图7 y 轴干扰估计Fig.7 y-axis disturbance estimation
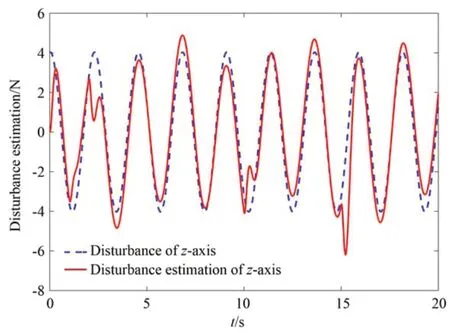
图8 z 轴干扰估计Fig.8 z-axis disturbance estimation
图6~图8 表示干扰估计情况,从图中可以看出,本文设计的干扰观测器可以对外部摄动干扰进行估计。
图9 表示状态估计情况,从图中可以看出,状态跟踪误差保持在较小范围内,能够实现对状态的跟踪。

图9 状态估计误差Fig.9 State estimation error
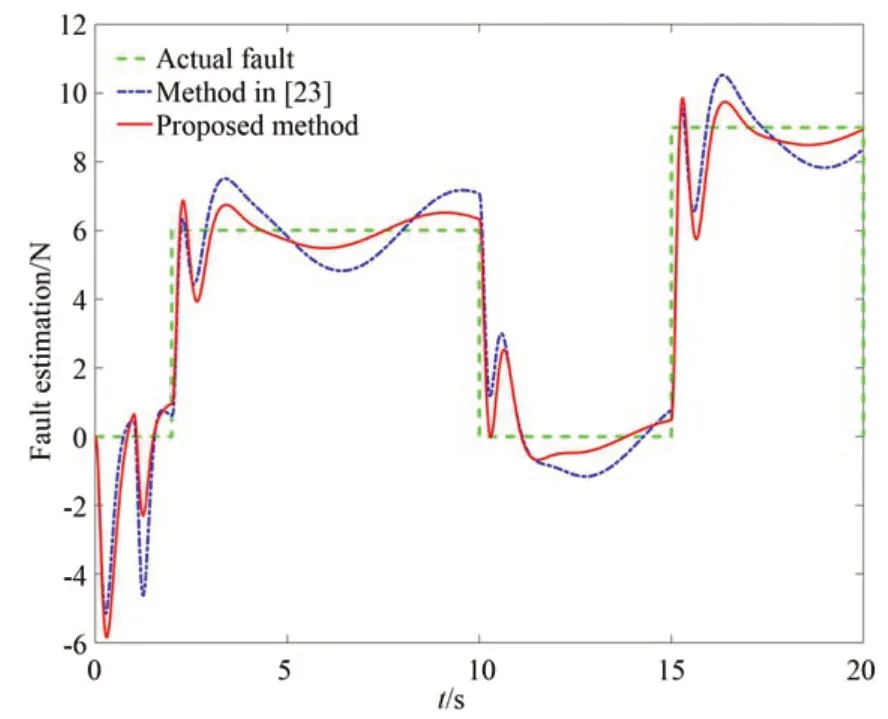
图10 y 轴间歇故障估计情况Fig.10 y-axis intermittent fault estimation
分别在x轴、y轴、z轴添加无故障模块、间歇性故障模块、时变故障模块,图10~图11 分别表示故障观测器对故障的估计情况,图中表明,文献[23]和本文提出的观测器均可以对故障进行估计,但相对文献[23]提出的观测器,本文提出的观测器对故障估计更为精确,性能有明显提高。

图11 z 轴时变故障估计情况Fig.11 z-axis time varying fault estimation
图12 表示系统存在模型误差、外部干扰以及执行器故障的情况下,以y轴控制效果为例,分别使用文献[22]提出方法、文献[23]提出方法以及本文提出方法,结合LQR 控制器,并加入前馈补偿项,对系统进行反馈容错控制,仿真结果表现,在使用文献[22]所提方法,即无干扰观测器时,系统具有十分明显的波动,难以达到稳态,说明H∞技术无法抑制全部干扰;使用干扰观测器情况下,控制效果得到改善,相比文献[23]所提方法,由于本文提出的观测器对模型误差、故障和干扰进行估计时,引入残差微分模块,并在容错控制时加入前馈补偿项,超调量明显降低,控制器精度提高了49.93%,能够满足双星编队精确构形保持控制目标。
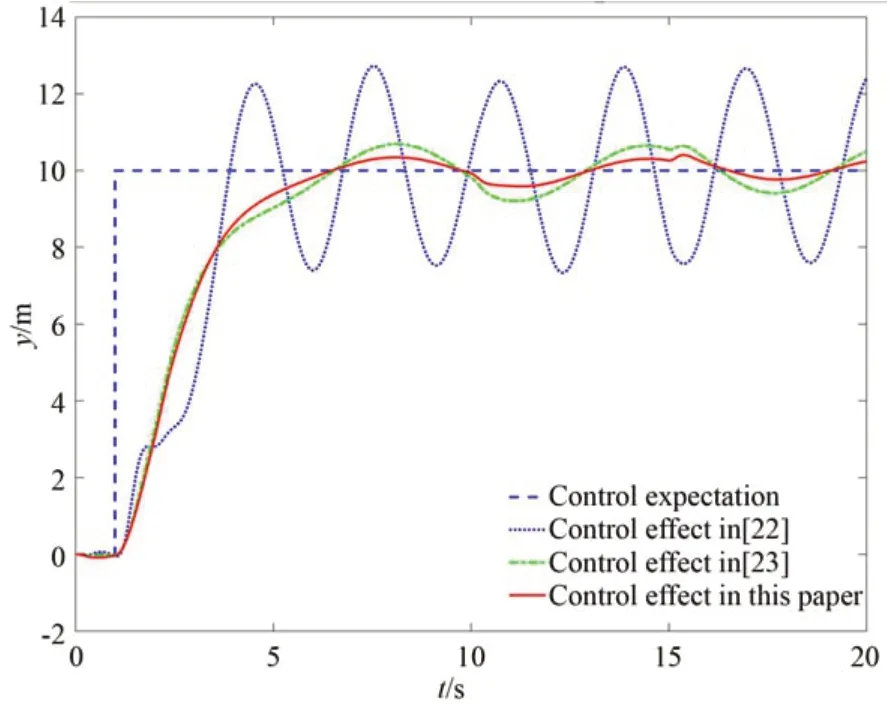
图12 控制效果对比Fig.12 Control effect comparison
6 结 论
本文对双星编队执行器故障估计的同时,考虑空间环境干扰的复杂性及轨道运动建模误差的影响,设计了一种可以综合估计系统模型误差、外部干扰以及执行器故障的增广观测器系统。另外,引入了残差微分模块,提高估计速度和准确度,采用了H∞方法,减小干扰中不可建模部分对控制系统的影响。最后,利用观测器对系统未知状态的估计信息,设计闭环反馈抗干扰容错LQR 控制律,并使用Lyapunov 稳定性理论证明了控制系统的稳定性。仿真结果表明,本文方法的控制精度提高了49.93%,证明了所提方法的有效性与优越性。
