大型空间离轴三反相机分体支撑结构设计
2021-04-22宋伟阳
宋伟阳 ,解 鹏 ,王 循
(1. 中国科学院长春光学精密机械与物理研究所,吉林长春130033;2. 中国科学院大学,北京 100049;3. 中国科学院天基动态快速光学成像技术重点实验室,吉林长春130033)
1 引 言
随着空间遥感技术飞速发展,人们迫切希望遥感相机可以做到高分宽幅的遥感观测,同时实现对广域空间的详查感知,极大地提高遥感相机的信息获取能力和观测效率。高分辨率和超大幅宽成像已成为新时期空间遥感的重要发展方向[1]。传统的空间遥感相机能做到高分辨率或大幅宽成像,但难以同时兼具高分宽幅的特性。现有空间大型离轴三反系统,其大视场、长焦距的特性可以同时实现米级分辨率、百公里级幅宽的成像指标[2]。而随着离轴遥感相机性能指标的提高,要求其外形尺寸也随之增大,且对相机结构稳定性要求的显著提升和结构非对称性的加剧成为影响成像质量的主要因素,因此合理的设计相机支撑结构是空间大型离轴三反相机研制的关键。
目前离轴三反遥感相机的主支撑结构形式主要有桁架式和框架式两种。日本于2020 年底发射的ALOS-3 遥感卫星,其光学载荷具有0.8 m 全色分辨率和50 km 幅宽,采用了桁架式支撑结构;席佳利通过有限元方法对某焦距为890 mm 离轴三反测绘相机的桁架式支撑结构进行了优化,实现了轻量化设计;安明鑫针对某离轴三反相机热稳定性要求,通过基于“类泊松效应”的热设计原理,研制了一种多层碳纤维消热桁架结构[3-5]。桁架结构轻量化程度高,但在整体性及稳定性方面存在劣势,应用于对结构尺寸变化更加敏感的大型高分宽幅遥感器时存在稳定性风险。框架式支撑结构整体性好,稳定性高,装调工艺简单,易于实现遥感相机的高刚度、高稳定支撑,国内外学者对框架式支撑结构也进行了很多研究。李丽富等通过拓扑优化的数学求解方法,设计了一种整体框架支撑结构,用于某主次镜间距360 mm 的小型离轴相机;美国Landsat-8 遥感卫星上的OLI 采用框架式支撑结构,在轨工作稳定;李畅等根据基于变密度理论的拓扑优化方法研制的一体式框架支撑结构,已成功应用于某离轴三反遥感相机[6-9]。但以往对于框架式支撑结构的研究,仅有针对体积较小的遥感器研制的一体式框架,对于尺寸超过1 m 的框架式支撑结构则因受材料成型工艺等因素的限制缺少相应的研究成果。
本文针对某1 m 分辨率、200 km 幅宽的大型空间离轴三反相机,建立了以整机基频为目标函数,以结构质量分数为约束条件的拓扑优化数学模型,建立了各分体支撑结构的二次尺寸优化数学模型,设计出了一种轻量化大型分体框架支撑结构。有限元优化分析与力学振动实验结果表明,优化所得的分体支撑结构能很好地满足空间大尺度离轴相机对支撑结构的刚度及稳定性要求。
2 支撑结构分体设计
2.1 设计约束
某型号高分宽幅遥感相机能够在500 km 轨道上实现1 m 的全色地面分辨率和200 km 幅宽的成像指标,实现对广域范围的详查观测。其光学系统如图1 所示:相机主次镜间距1 810 mm,主镜有效通光口径为1 800 mm×500 mm,主镜、三镜、折叠镜镜长度均超过1 500 mm,长宽比均大于3.5,结构非对称性十分显著,反射镜结构参数如表1 所示。此外相机结构需要具有高刚度和轻量化的特性,要求支撑结构总质量不大于230 kg,整机基频不低于50 Hz。
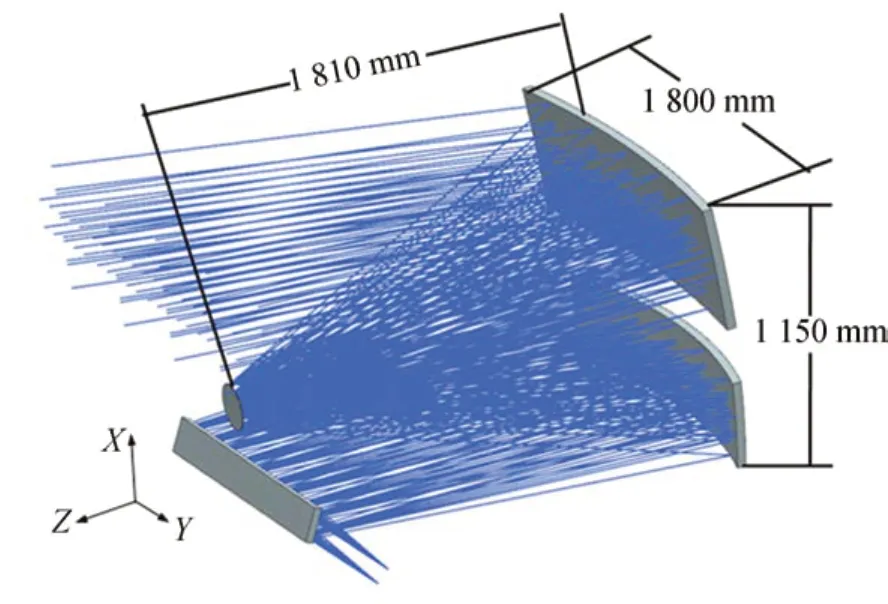
图1 离轴三反光学系统Fig.1 Off-axis three mirror optical system
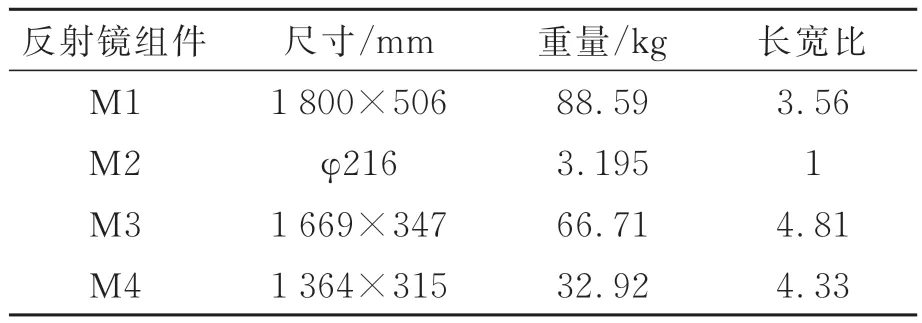
表1 反射镜结构参数Tab.1 Structural parameters of reflector
各反射镜组件的相对位置关系影响相机成像质量,为了获得良好的像质,光学设计要求反射镜组件位置精度要求见表2。
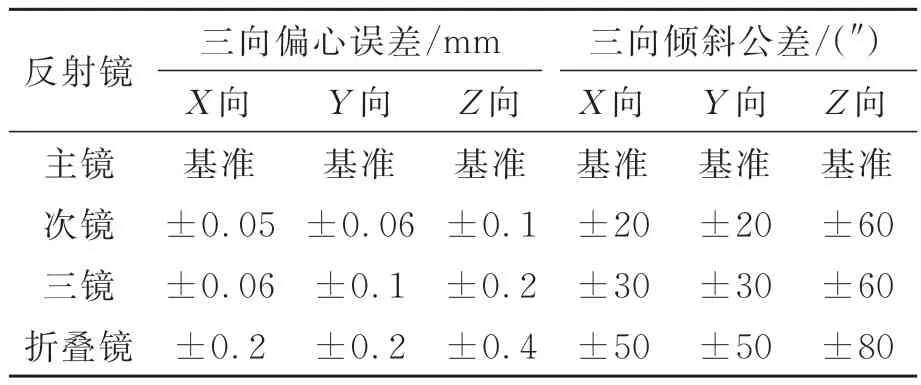
表2 相机装调公差Tab.2 Camera alignment tolerance
2.2 主支撑结构材料选择
空间相机支撑结构材料选择主要考虑材料的比刚度、热稳定性和加工工艺性等[10-12]。目前常用于空间相机主支撑结构的材料主要有铝合金、钛合金、高体份SiCp/Al 和碳纤维复合材料等[13-14],材料的物理性能如表 3 所示。其中,铝合金热稳定性较差,受热不均时容易引起局部变形;钛合金具有成熟的加工工艺和良好的尺寸稳定性,但比刚度较低,不利于进行光机结构的轻量化设计;碳纤维复合材料在结构轻量化上具有较大优势,但其成型工艺复杂,热稳定性较差,且碳纤维复合材料容易吸收空气中的水分产生内应力,引起结构变形,以上材料均不适用于本文中的大型空间相机支撑结构。高体份SiCp/Al 复合材料具有很好的力学性能,其比刚度远高于其他金属材料,且热稳定性良好,加工工艺成熟,被广泛应用于航天机械结构件。综合以上分析,选取高体份SiCp/Al作为相机支撑结构的材料。
2.3 支撑结构分体设计
本文中的遥感相机尺寸较大,支撑结构最大尺寸超过2 m,受材料成型工艺限制,无法采用一体式框架支撑结构,因此本文通过对框架式支撑结构进行分体设计的方案,实现对该大型空间遥感相机的高刚度、高稳定支撑。

表3 几种空间材料特性对比Tab.3 Comparison of some structural materials in space
根据光学系统布局特点,将主镜、三镜固定在后反射镜安装板上,便于在装调过程中实现主、三镜共基准;同理,次镜和折叠镜安装在前反射镜安装板;由于相机尺寸较大,因此在结构内部设置中心支撑板,增加框架结构的刚度及整体性;此外,为了减小相机外包络,降低支撑结构的总重量,在设计侧面支撑板时尽量贴合光线,使结构更加紧凑。经过初步的构型设计,完成了框架支撑结构分体构型方案,支撑结构分为以下9个部分:①前反射镜安装板、②后反射镜安装板、③入光板、④焦面板、⑤中心支撑板、⑥+Y上侧板、⑦-Y上侧板、⑧+Y下侧板、⑨-Y下侧板,如图2 所示。
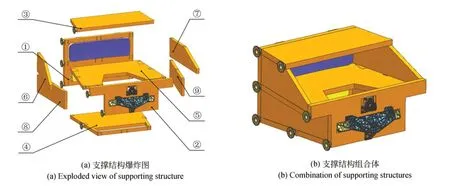
图2 分体支撑结构初始构型Fig.2 Initial configuration of split support structure
经过分体设计后,相机支撑结构外形包络为 1 378 mm×1 990 mm×2 250 mm,总重量为3 729.6 kg。接下来需要对支撑结构进行优化,提高材料利用率,提升结构比刚度,得到轻质量、高刚度的框架式支撑结构。
3 支撑结构优化设计
3.1 拓扑优化设计
3.1.1 数学模型
拓扑优化已经被广泛应用于空间相机结构设计和优化,是一种重要的结构轻量化方法。遥感卫星所处的力学环境一般较为恶劣,通常希望空间相机整机的基频较高,避免火箭发射时的低频正弦加速度载荷引起空间相机与卫星平台发生共振,造成结构破坏。在空间相机各个结构分系统中,相机支撑结构的空间跨度最大,往往对整机刚度、基频具有决定性影响[15-16],因此有必要以基频为优化目标对相机支撑结构进行拓扑优化设计,以确定最有效的材料分布。以相机基频最大为目标函数,以体积分数及反射镜刚体位移为约束条件,建立拓扑优化数学模型:
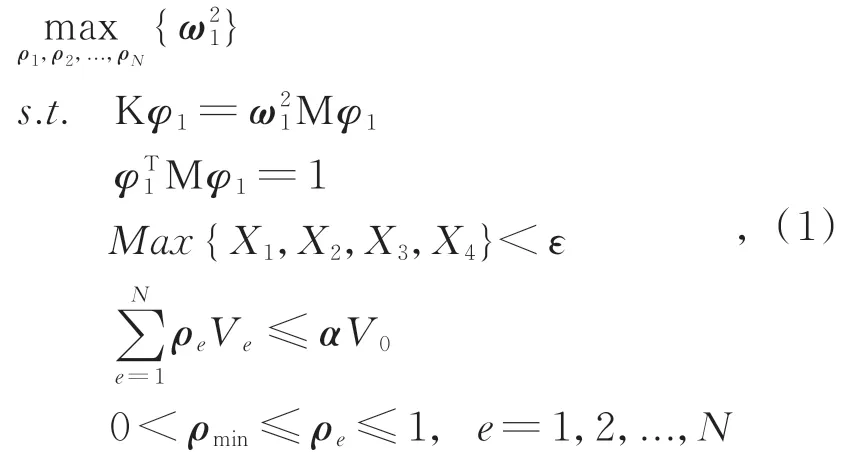
其中:Ve为单元e的体积,ρe(e=1,2,...,N)为单元e的密度,是材料密度与惩罚因子的乘积;N为单元总数;ω1为第 1 阶特征频率;φ1为第 1 阶特征向量;K和M分别为对称的正定刚度矩阵和质量矩阵;X1,X2,X3,X4分别为四个反射镜组件在重力载荷下的刚体位移,ɛ是反射镜组件刚体位移的光学公差;ρmin是最小单元密度,为了避免矩阵奇异设定ρmin≥1×10-3;V0为设计域的体积;α为设计域的体积分数。
3.1.2 优化过程
由于前后框架板需要安装反射镜组件,优化空间有限,因此设定前后反射镜安装板为非优化区域,以质量点代替安装在支撑结构上的反射镜组件,建立结构拓扑优化有限元模型,如图3 所示。其中,优化的目标函数为相机整机的基频最大,约束条件为优化区域的体积分数及反射镜刚体位移,设计变量为单元密度。
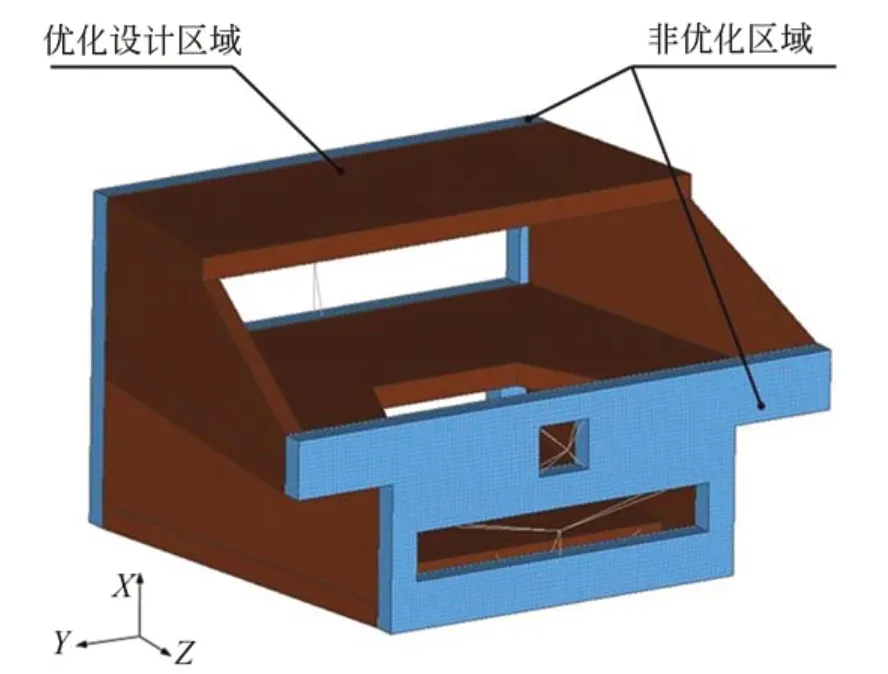
图3 空间相机框架有限元模型Fig.3 FEM model of space camera frame
经过迭代计算后,得到拓扑优化结果如图4所示。侧板通过斜筋连接前后反射镜安装板;入光板一侧中心通过斜横梁与另一侧相连;中心支撑板内为一个“∧”字形的横梁结构,起到了提高结构刚度的作用。
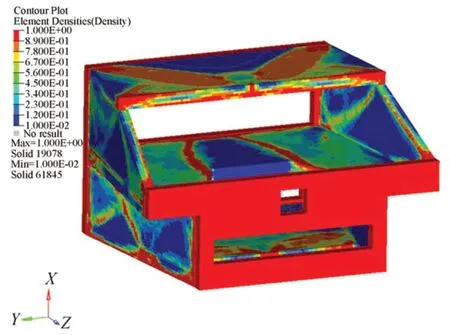
图4 拓扑优化结果Fig.4 Topology optimization results
拓扑优化计算结果清晰地展示了支撑结构在要求整机基频最大时的最佳材料分布,结合工程实际进行构型和轻量化设计,最终确定相机框架的设计方案如图5 所示。该状态下分体框架总质量为296.1 kg,轻量化率达到了92.06%。
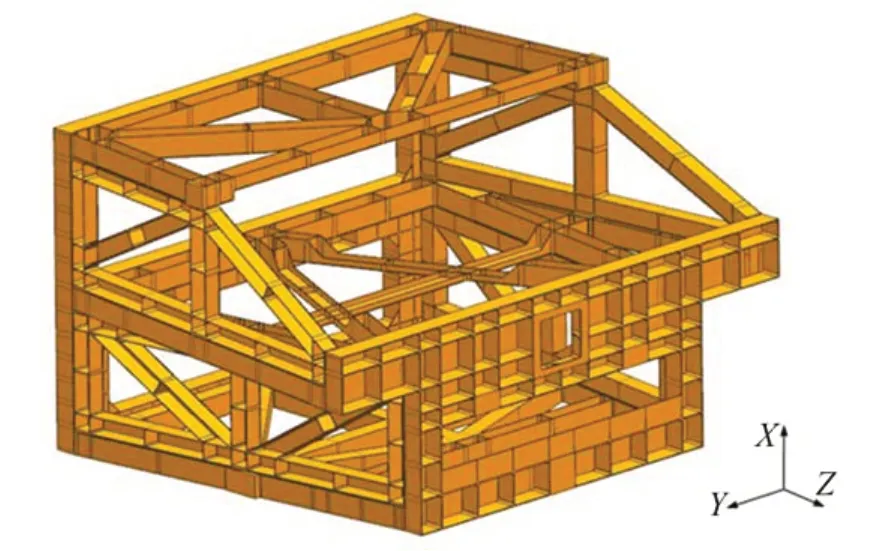
图5 拓扑优化后空间相机框架模型Fig.5 Space camera frame model after topology optimization
3.2 尺寸优化设计
3.2.1 数学模型
前文通过以基频最大为目标函数的拓扑优化得到了分体支撑结构的最佳材料分布。虽然在有限体积内,支撑结构确定了合理的结构形式,但框架结构内的具体尺寸参数没有达到最优。为了在确定的结构形式下进一步提高整机基频,需要再次以整机基频最大为目标函数对各分体结构局部尺寸进行优化。以分体结构总质量为约束,以单元厚度作为设计变量,以基频最大为目标函数建立数学模型:
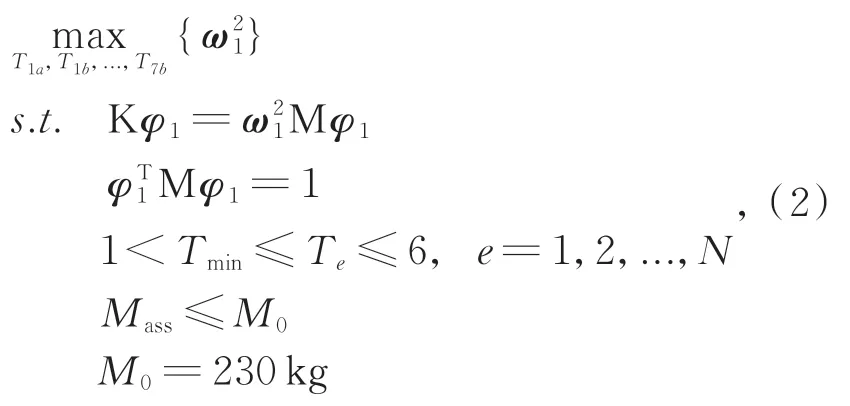
其中:ω1为结构一阶固有频率;K,M分别为系统的刚度矩阵和质量矩阵;φ1为与ω1对应的特征向量;Te和Tmin分别为单元厚度及最小单元厚度;Mass为总质量,M0为约束质量。
3.2.2 优化过程
为了保证加工工艺性和设计的合理性,优化时分体结构中的尺寸参数不宜过多,因此将框架中9 个分体结构编号后,设定Tia,Tib两个参数,分别表示第i块分体结构中加强筋和承力板的厚度,建立分体支撑结构尺寸优化有限元模型,如图6 所示。以整机基频最大为目标函数,以分体支撑结构总质量不大于230 kg 为约束,以个各分体支撑结构中具体尺寸参数为设计变量进行优化计算。
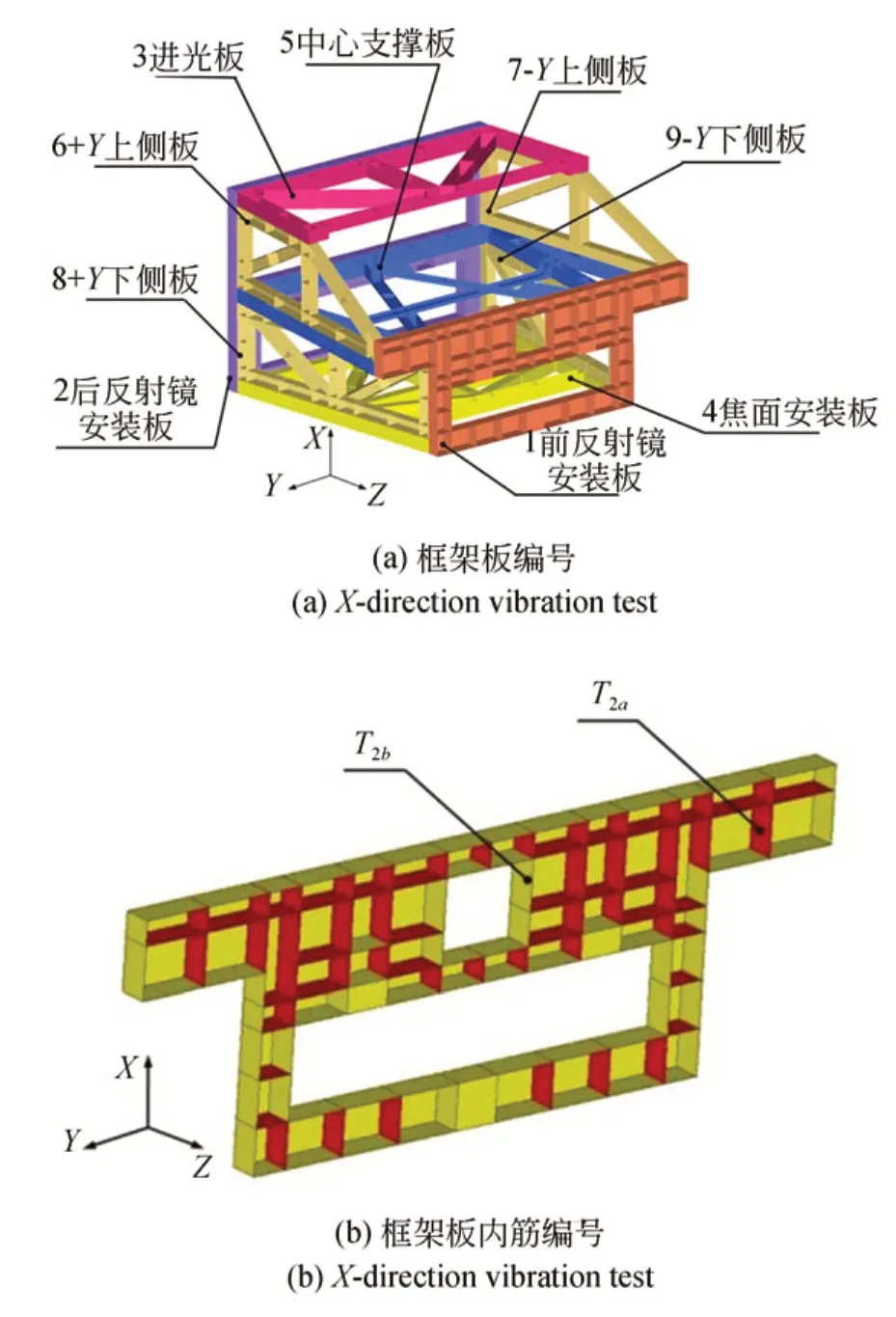
图6 尺寸优化有限元模型Fig.6 FEM model of size optimization
通过迭代计算,得到了9 块分体支撑结构的具体尺寸参数,对优化结果合理取值后结果如表4 所示。可以看出,前后安装板作为安装反射镜的结构直接承受载荷,其结构尺寸取值较大;-Y侧板由于远离约束位置,其结构尺寸比+Y一侧明显减小;中心支撑板中各尺寸参数均大于优化区间中值,表明其对结构整体刚度具有较大贡献,验证了设置中心支撑板的必要性。
通过对分体支撑结构进行拓扑优化和尺寸优化,得到了各部分结构的最佳构型和框架各部分的最优尺寸。经过设计,分体框架支撑结构总重量为227.8 kg,轻量化率达到93.9%,满足该相机对支撑结构的轻量化设计要求。
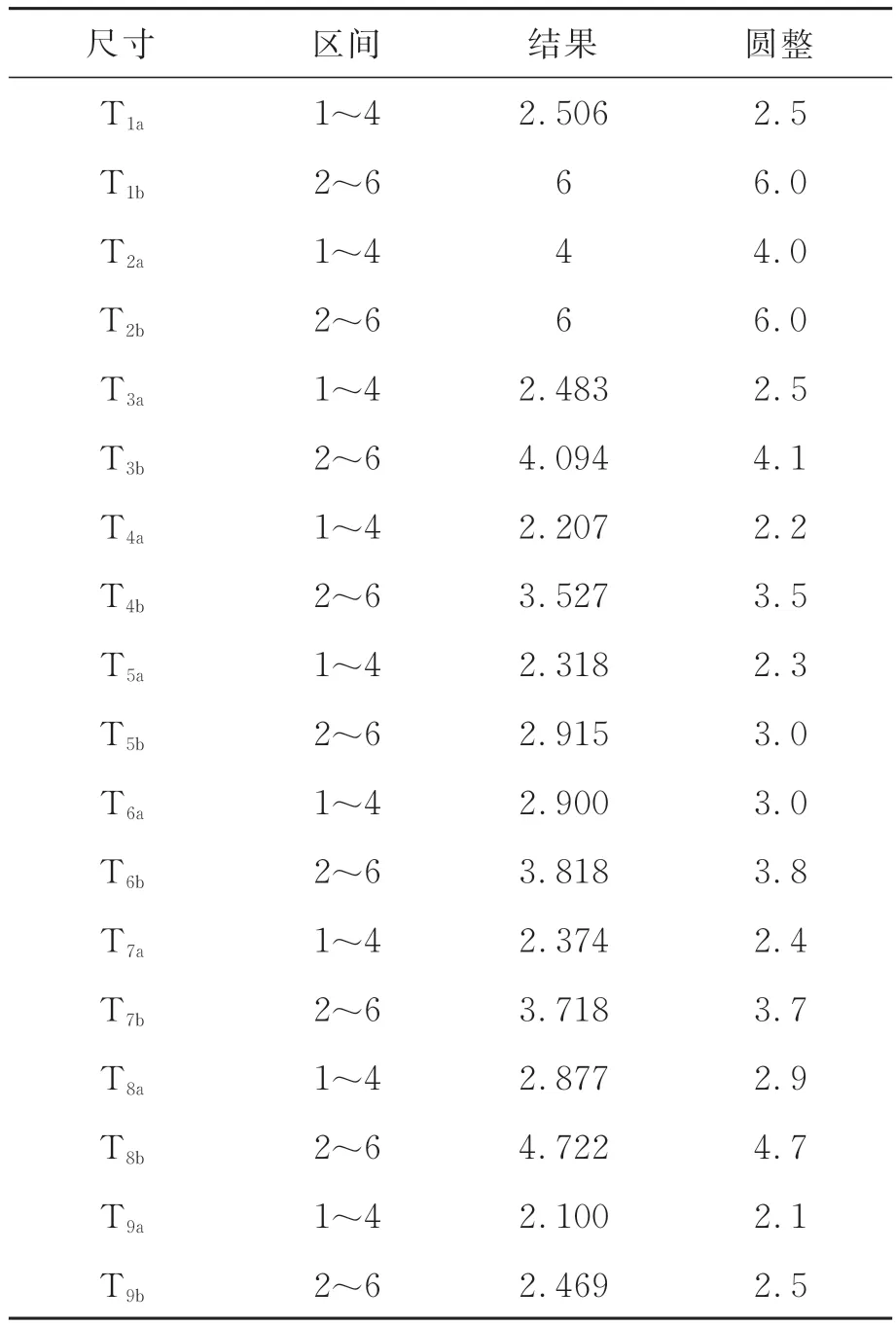
表4 尺寸优化结果Tab.4 Result of size optimization (mm)
4 分析与验证
4.1 模态分析
模态分析是计算结构固有频率的主要手段之一,能够提供给定约束下的固有频率和振型,考察结构的动态刚度,评价其力学性能[17]。现建立主支撑结构有限元模型,带入到空间遥感相机的整机模型中,约束相机与卫星平台的连接位置,设置高体份SiCp/Al 为分体支撑结构材料进行约束模态分析,结果如图7 所示。
分析结果表明,相机一阶固有频率为51.47 Hz,该阶次固有频率下的振型为相机整体沿X 轴的摆动。出于经济性考虑,后续研究中将采用铝合金材料制造相机力学样机进行实验验证,因此修改模型中支撑结构材料为铝合金,保持框架构型、尺寸及与镜组的连接接口不变,再次进行模态分析。分析结果表明,铝合金力学样机一阶固有频率为29.08 Hz,前三阶模态振型与使用高体分SiCp/Al 材料时基本相同,各阶频率均有降低,验证了分体支撑结构的合理性,体现了高体分SiCp/Al 材料性能上的优越性。
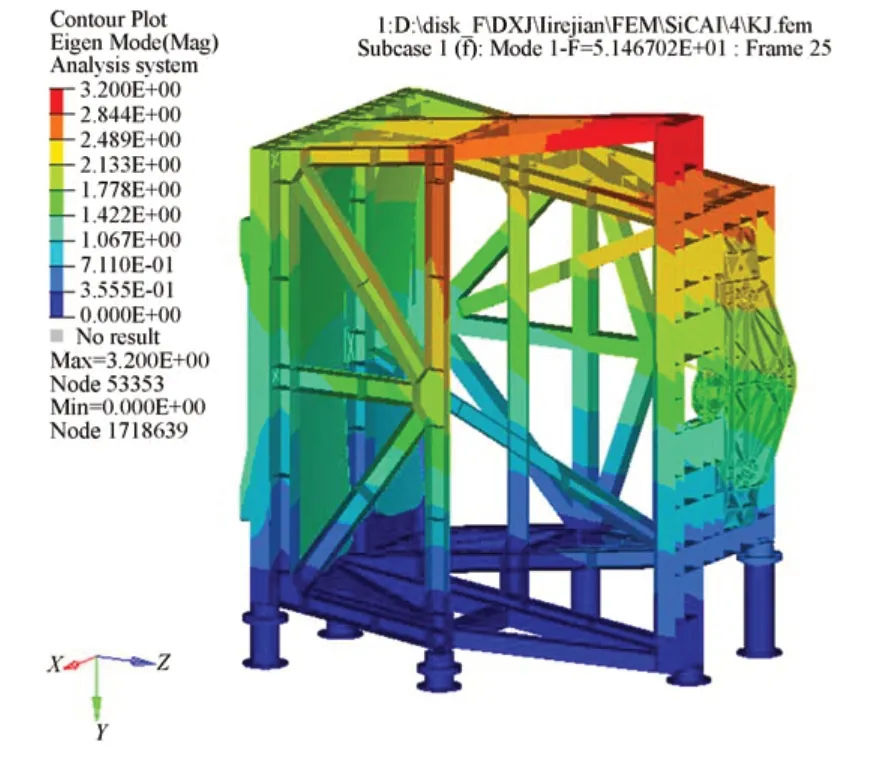
图7 一阶模态振型Fig.7 First modal shape
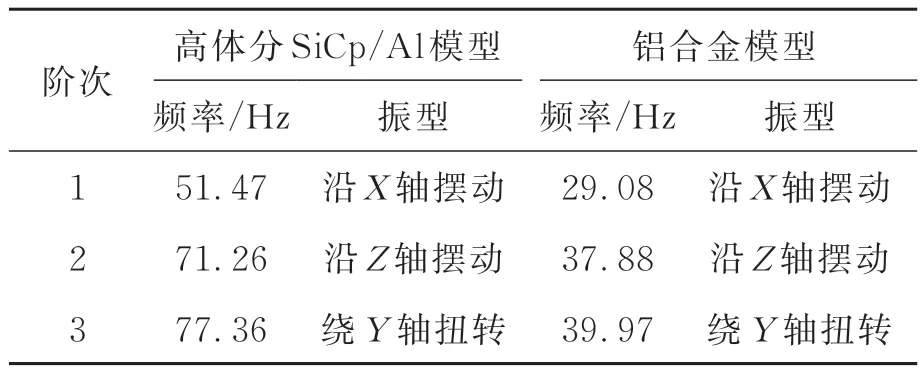
表5 模态分析结果对比Tab.5 Comparison of modal analysis results
4.2 热变形分析
遥感相机工作环境的温度条件十分复杂,环境温度变化引起的结构变形也是影响遥感相机成像质量的重要原因。为了考察支撑结构的热稳定性,建立了相机的热分析模型,计算该遥感相机在整体温度提高5 ℃的情况下各个反射镜的变形情况,变形云图如下图所示。
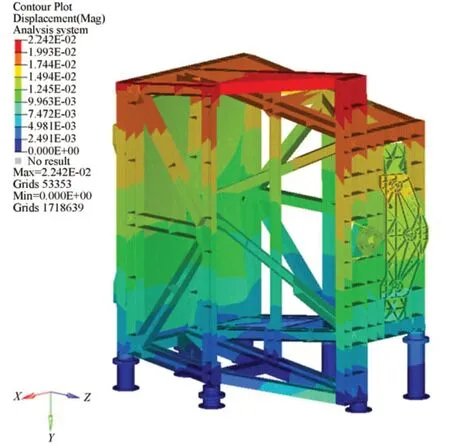
图8 升温5 ℃变形云图Fig.8 Deformation nephogram of rising by 5 ℃
考察相机结构热稳定性时,以反射镜相对位置变化作为评价指标。在5 ℃温升的工况下,次镜、三镜、折叠镜相对于主镜的刚体位移和转角如表6 所示。其中次镜和折叠镜相对于主镜的刚体位移在Z向最大,分别为 15 μm 和 16.2 μm;折叠镜相对于主镜的转角在X和Y方向较大,分别达到2.42″和3.19″;各个反射镜的刚体位移和转角均在公差要求范围之内,证明了该框架式分体支撑结构具有良好的热稳定性,能满足遥感相机的使用要求。

表6 反射镜组件升温5 ℃变形Tab.6 Deformation of the mirrors after heating up 5 ℃
4.3 扫频实验
扫频实验是对结构施加某一方向的动力学载荷后记录观察其响应状态,获取结构模态信息,验证有限元分析准确性和结构设计合理性的有效方法[18]。根据模态分析的一阶频率结果,对力学样机进行X方向的扫频及正弦实验,为了考察关键位置及薄弱结构的响应情况,将传感器布置在各个反射镜及结构约束远端的位置,如图9所示。

图9 整机振动试验现场Fig.9 Frequency vibration test site
对力学样机在X方向的正弦扫频实验结果如图10 所示。可以看出,样机在X方向的一阶频率为28.3 Hz,与模态分析中一阶频率29.08 Hz相差2.68%;频率偏差在5%以内,从工程应用角度验证了分体支撑方案的合理性和有限元分析的准确性。
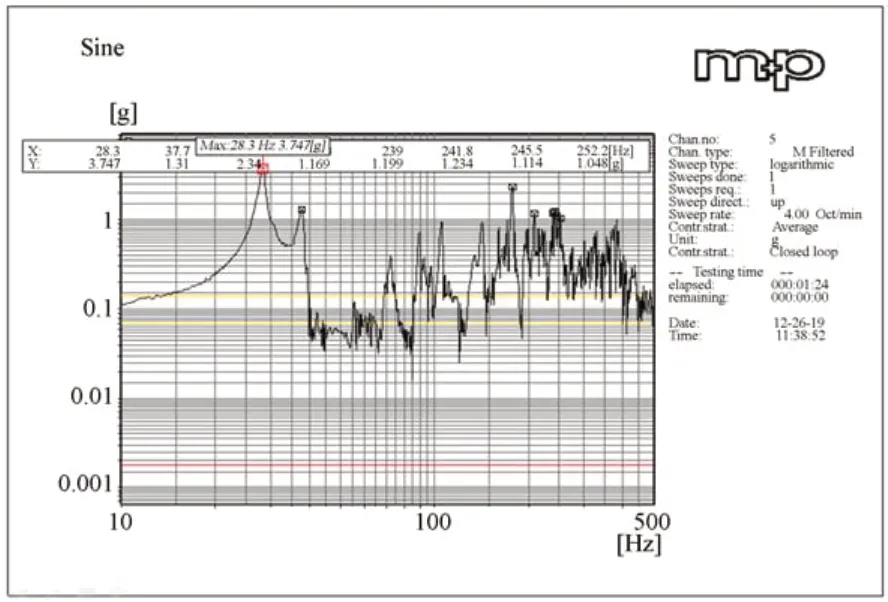
图10 扫频试验结果Fig.10 Frequency sweep test results
4.4 动力学载荷下的稳定性检测
为了验证分体支撑结构在动力学载荷下的稳定性,保证各反射镜组件在经历发射阶段动载荷后具有足够的位置精度,在相机振动试验前后分别进行了棱镜角度标定。具体做法是,在所有反射镜组件上设置标定棱镜,通过经纬仪对所有棱镜的俯仰角进行标定,以主镜上的标定棱镜为基准,计算得到振动前各反射镜组件相对于主镜组件的角度差值Δθ。在振动试验后,以相同的方式得到振动后的各个反射镜组件相对于主镜组件的位置偏差Δθ′,通过比较Δθ和Δθ′,分析分体框架支撑结构在振动实验前后的稳定性。根据上述原理,搭建了如图11 所示的实验平台。

图11 稳定性检测现场Fig.11 Stability testing site
从表7 所示的实验结果可以看出,在振动前后的两次标定试验中,主镜组件的俯仰角发生了变化,这是由于力学样机在两次试验中主镜位置偏差引起的,属于稳定性试验中的系统误差。分别求得各反射镜组件相对于主镜组件的位置偏差变化∣Δθ-Δθ′∣后发现,次镜、三镜、折叠镜组件在振动实验前后均产生了相对于主镜组件的变形,其中次镜变形量最小为7″;折叠镜变形量最大为22″。力学样机各反射镜组件相对于主镜的偏差在振动实验前后变化明显优于光学公差要求,说明了力学原理样机在面对动载荷时具有良好的稳定性,证明了所设计的相机分体支撑结构具有高刚度、高稳定性的特点。

表7 振动前后反射镜偏移Tab.7 Mirror offset before and after vibration
5 结 论
本文针对某大型空间离轴三反相机高刚度、轻量化的支撑需求,通过对整体框架支撑结构的分体设计,完成了该相机的支撑任务。通过整合拓扑优化和尺寸优化的优化链路,得到了支撑结构的最佳构型和尺寸。设计后的分体支撑结构总重227.8 kg,轻量化率达到93.9%。有限元分析结果表明,分体支撑结构能保证相机整机基频大于50 Hz,满足结构刚度需求;温升5 ℃工况下各反射镜组件偏移量均在光学公差范围内。对力学样机进行动力学及稳定性实验,实验结果与有限元分析误差小于5%,满足工程需要;振动实验前后反射镜组件相对角度偏差变化不超过22″,明显优于光学公差要求,说明分体支撑结构具有良好的稳定性,验证了拓扑优化和尺寸优化的准确性与合理性。文中所设计的框架式分体支撑结构具有工程应用价值,可以为其他大型空间相机支撑结构提供一种新的设计思路。
