对Auslander类和Bass类的进一步研究*

王善策， 张 珍

(齐鲁师范学院数学学院，250200，山东省济南市)

0 引 言

交换诺特环上的半对偶化模最初是由 Foxby[3]、Golod[4]和 Vasconcelos[5]分别以秩为 1 的PG-模、suitable 模和 spherical模三个不同的名字引入并研究的.半对偶化模(复形)在模论、环论、表示论中扮演了重要的角色.设C是一个半对偶化模，很多情况下，半对偶化模可以代替环自身的正则模，从而可以推广很多经典同调代数中的结论.并且，半对偶化模C诱导了一些有趣的模类，像C-投射模类，C-内射模类，C-平坦模类.最近，Holm 和 White[7]在一般结合环上定义了半对偶化双模，以及 Auslander 和 Bass 类，并用C-投射模，C-内射模刻画了Auslander 和 Bass 类.由半对偶化模C诱导的相对同调代数引起了国内外大量专家学者的关注，并且大家把目光聚焦在关于Auslander 和 Bass 类的研究上.值得注意的是，在非交换、非诺特环上，Holm 和 White[7]引入了 Foxby 等价的内容，即，所有的C-内射R-模都包含于 Auslander 类Ac(R)中，所有的C-投射(平坦)S-模都包含于 Bass 类Bc(S)中.

本文的第一个结果，即通过引入偏 Auslander 类 (Bass 类)，推广了传统的 Foxby 等价,即定理 2.1.

当R是一交换环，C是R上的一个半对偶化双模时，Takahashi and White[9,Corollary 2.4]证明出Auslander类Ac(R)中的所有模都有正和的properC-内射分解，Bass类Bc(R)中的所有模都有正和的 properC-投射分解.

本文的第二个结果证明出上述结论的逆也是成立的，即，具有properC-内射分解(C-投射分解)的模一定在Auslander类Ac(R)(Bass类Bc(R))中.因此，本文部分推广了Takahashi 和 White[9,Corollary 2.4]的结果即注2.2.

1 预备知识

本文假设R是含有单位元的结合环.首先，引入一些概念，这些概念被Avramov,Martsinkovsky[1],Holm[5]以及 SatheR-Wagstaff,Sharif 和 White[8-10]所使用.

定义1.1 设χ是一右R-模类，M是一右R-模.M的一个χ-分解是指M含有如下的一个正合序列：…→X1→X0→M→0，其中Xi∈χ，i≥0. 如果对于任意的X∈χ，序列…→HomR(X,X1)→HomR(X,X0)→HomR(X,M)→0仍然是正和的，则…→X1→X0→M→0称为M的一个properχ-分解.对于M的χ-余分解和properχ-余分解可以类似的定义.

定义1.2[7]一个 (S,R)-双模sCR称为半对偶化的，如果它满足下面5条：

(1)sC有一个S-投射分解，并且分解式中的每一项都是有限生成的左S-投射模;

(2)CR有一个R-投射分解，并且分解式中的每一项都是有限生成的右R-投射模;

(3) 自然的同伦映射sSs→ HomR(C,C)是一个同构；

(4) 自然的同伦映射RRR→ Homs(C,C)是一个同构；

定义1.3[7]设sCR是一半对偶化双模. 由C诱导的AusLander类Ac(R)是由满足下列条件的左R-模M构成的集合：

(3)自然的赋值同态映射μM:M→ Homs(C,C⊗RM) 是一个同构.

由半对偶化模C诱导的 Bass 类Bc(S)是由满足下列条件的左S-模N构成的集合：

(3)自然的赋值同态映射μN:C⊗RHoms(C,N)→N是一个同构.

设sCR是环S和R上的半对偶化双模.本文中，为了方便书写，我们用符号Hc代替函子Homs(C,-);用Tc代替函子C⊗R-.

对于任意的左R-模X和左S-模Y，符号μX:X→HCTC(X)和υY:TCHC(Y)→Y代表两个自然的赋值同态映射.

2 主要结果

首先，给出偏Auslander类和偏Bass类的概念.

(2) 自然的赋值同态映射μM:M→ Homs(C,C⊗RM) 是一个同构.

(2)自然的赋值同态映射υN:C⊗RHoms(C,N) →N是一个同构.

命题2.1 设0 →L→M→N→ 0 是一左R-模正和序列，并且在函子Tc下仍保持正和.

证明只证(1)，(2)的证明和(1)类似.

由假设知，存在一个正和序列：0→TC(L)→TC(M)→TC(N)→0.对该正合序列应用左正合函子HC，得到如下交换图：

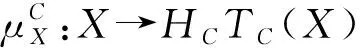
首先证明下列范畴间的等价，该等价补充了经典的Foxby等价，是文献[7,Proposition 4.1]的一个推广.

(2)的证明与(1)类似.

由定义知，AC(R)⊆CT∩Fix(μC)，BC(S)⊆C⊥∩Fix(υC).因此通过命题2.2有定理2.1.

定理2.1 下述表格推广了Foxby等价.

设Ic(R)代表C-内射R-模类，coresIc(R)代表具有一个properC-内射余分解的左R-模构成的集合,Pc(S)代表C-投射模类，resPc(S)代表具有一个properC-投射分解的左S-模构成的集合，见定义1.1.

命题2.3 对于任意的左R-模M和左S-模N，有

证明只证明(1)，因为(2)的证明和(1)类似.

由文献 [7,Proposition 5.3(b)(c)]知，Ic(R) 在任意结合环R上都是一个包络类.

由定义1.1知M∈coresIc(R) ⟺M有一个properC-内射余分解Δ，即Δ=0→M→HC(I0)→HC(I1)→…→HC(Ii)→…，对于任意的i≥0，Ii都是内射左S-模.且该C-内射余分解Δ在函子HomR(-,HC(E))(E是任意内射R-模)下是正合的.由Hom-tensor的伴随性同构知，该C-内射分解Δ在函子TC下是正合的，即序列TC(Δ)=0→TC(M)→TCHC(I0)→TCHC(I1)→…→TCHC(Ii)→…是正合的.因为Ii是内射的，所以TCHC(Ii)≅Ii.因此有

(1)HCTC(Δ)≅Δ⟺HCTC(M)≅M；

定理2.2 设sCR是一个半对偶化双模.

(3)的证明方法对偶于(1),故省去证明.

注2.2 由命题2.3和定理2.2知，当CR的平坦维数有限(sC的投射维数有限)时，具有properC-内射余分解(properC-投射分解)的左R-模(左S-模)一定在Auslander类Ac(R)(Bass类Bc(S))中，即Takahashi和White的结论[9]的逆命题是成立的.