基尔霍夫型方程的无穷多解

张 琪, 栾世霞

(曲阜师范大学数学科学学院,273165,山东省曲阜市)

0 引 言

本文主要研究下述基尔霍夫型方程

(1)

a为常数且a>0,λ是一个参数,f∈C(N×,),F(x,u)=f(x,s)ds,s∈N.

过去几十年间,问题 (1) 是一个重要的非局部拟线性问题.因为当f满足不同的条件就会得到不同的结果,所以这类基尔霍夫问题及其结果已经得到了广泛的研究.例如,文献[4]在f满足超线性的条件下,通过变分方法和扰动方法得到了基尔霍夫问题的无穷多解.文献[13]在f满足渐近线性的条件下,利用极大极小方法和莫斯理论,得到了共振和非共振条件下基尔霍夫型方程的3个非平凡解的存在性.文献 [18]提出当f满足适当的控制增长条件,通过最小化的讨论,得到基尔霍夫型方程的最小能量变号解.另外,当f满足奇性条件,利用定量形变引理,得到基尔霍夫型方程的无穷多非平凡弱解.

当V(x)=0,λ为正常数,N被一个有界区域 Ω 取代时,问题 (1) 就简化为下述问题

(2)

基尔霍夫在文献 [1] 中首次提出此方程.准确来说,与拟线性基尔霍夫方程

密切相关,是自由振动弹性绳的经典达朗贝尔波方程的扩展.自此方程提出后,方程 (2) 备受关注,早期的研究成果见文献 [5-7].事实上,在各种物理和生物模型的研究中,基尔霍夫问题也受到越来越多的关注[8-12,14].

在主要结果证明前,我们假设V(x),f(x,u) 满足以下条件:

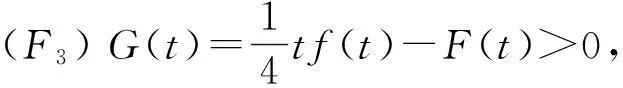
(F5)f(x,-t)=-f(x,t),t∈,x∈N.

利用喷泉定理来求泛函的解,需验证(PS)条件成立.首先,由于在全空间H1(N) 上,很难验证(PS)序列的有界性,其次,由于非局部项∇u|2dx的影响,得到一个有界的(PS)序列时,对于∇∇u|2dx极限的成立仍面临着困难.为了解决这些困难,我们使用径向对称的索伯列夫空间N).N) 为H1(N) 的子空间.于是,定义泛函N)→

(3)

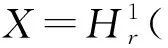
1 预备知识和主要结果

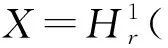
Bk={u∈Yk:‖u‖≤ρk},Nk={u∈Zk:‖u‖=rk}, 且ρk>rk>0.

ci定义了不同的正常数.

定理1.1 假设 (V1),(F1)-(F5) 成立,则存在λ*>0,当λ∈(0,λ*) 时,问题 (1) 有无穷解uk,使得当k→∞ 时,Iλ(uk)→+∞.

2 引理及主要结果的证明

因为Iλ∈C1,所以,对任意v∈X有

(4)

我们先介绍一下喷泉定理.

引理2.1[2]假设泛函φ∈C1(X,) 满足φ(-u)=φ(u)，对于几乎处处的k∈,存在ρk>rk>0,使得

(ⅲ) 对任意的C>0,φ满足 (PS)c条件;

则φ有一个无界的临界值序列φ(uk)→+∞,k→∞.

引理2.2 假设条件 (V1),(F1)-(F3) 成立,则

(a) 存在ρ>0,α>0,使得Iλ(u)≥α>0,u∈X且 ‖u‖=ρ.

(b) 存在e∈X,‖e‖>ρ,λ*>0,当 0<λ<λ*时,Iλ(e)<0.

证明(a) 由条件 (F1) 和 (F2) 知,对任意的ε>0 有cε>0,使得

(5)

由索不列夫嵌入不等式,有

所以,由上式知,当 ‖u‖=ρ>0,ρ充分小时,有Iλ(u)≥α>0,即(a)成立.

因此,存在e∈X,‖e‖>ρ且Iλ(e)<0,其中 0<λ<λ*,于是(b)成立.

引理2.3[3]设E为巴拿赫空间,E*为E的对偶空间.φ∈C1(E,),存在α<β,ρ>0,u1∈E且‖u1‖>ρ，满足条件设其中 Λ={γ∈C([0,1],E):γ(0)=0,γ(1)=u1} 是连接 0 和u1之间的连续路径的集合.则存在 {un}⊂E,使得

I(uk)→c≥β,I′(uk)→0，k→∞.

由引理2.2和引理2.3,可知,存在一个 (PS) 序列 {uk}⊂X,满足

Iλ(uk)→c>0,Iλ′(uk)→0，k→∞

(6)

引理2.4 假设条件 (V1) 和 (F3) 成立,则 (PS) 序列 {uk} 在X中有界.

证明由 (6) 式得,

(7)

反证,假设 {uk} 在X中无界,即当k→∞ 时,‖uk‖→+∞.由不等式 (7) 及条件 (F1),若 {uk} 无界,则 (7) 式矛盾,所以 {uk} 在X中有界.

引理2.5 若 {uk}在X中有界,且当k→∞ 时Iλ′(uk)→0,则 {uk} 在X中有一个收敛的子列,为书写方便,仍记为 {uk}.

接下来证明 {uk} 有强收敛子列

〈Iλ′(uk)-Iλ′(u),uk-u〉=

(8)

显然,当n→∞ 时,等式左边和等式右边的中间两项趋于 0.另外,由文献[2]的定理 A.2,可以得到

f(x,un)→f(x,u),在Lq(N)中

由 Hölder 不等式可知

定理1.1的证明由引理2.2,引理2.3,引理2.4可以得到有界的 (PS) 序列.由引理2.5,可知道Iλ(u) 满足引理2.1的条件 (ⅲ).另外,由条件 (F5) 知,Iλ满足Iλ(-u)=Iλ(u).下面证明Iλ(u) 满足引理2.1中的条件 (ⅰ) 和 (ⅱ).

首先验证 (ⅰ),有条件 (F1),(F3),(F4) 知,存在常数ci>0,i∈,使得

F(x,u)≥c3|u|4-c4|u|2.

则

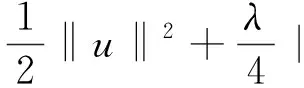
因为在有限维空间Yk中范数等价，所以,当 ‖u‖=ρ,ρ充分大时,(ⅰ) 满足.

其次验证 (ⅱ),由条件 (F1),得

(9)

定义

(10)

由文献[2]知,当k→∞,βk→0.所以,在空间Zk中,由 (9),(10) 式及索不列夫嵌入不等式,得

(11)

取

(12)

因为p>2,所以当k→∞,rk→+∞.将 (12) 式代入 (11)式,得

当k→∞,所以,条件 (ⅱ) 成立.综上,定理1.1得证.