四阶非局部基尔霍夫方程的多重解*

张海燕, 莫 帅, 赵月云, 毛安民

(曲阜师范大学数学科学学院,273165,山东省曲阜市)

0 引 言

本文讨论如下一类重要的四阶椭圆型方程

(*)

设V(x)=0,q(x)≡1,3被光滑区域Ω⊂3所代替,并且在∂Ω上u=∇u=0,则问题(*)转化为下述四阶基尔霍夫方程

在文献[3]中,Ma运用变分方法来研究非局部四阶基尔霍夫方程

的正解的存在性以及多重性.

在问题(*)中,当a=1,b=0,且q(x)=1时,在N上问题(*)便转化为著名的四阶椭圆型方程

(**)

对问题(**)的研究已有很多工作. 例如,Yin和Wu[8]通过利用山路定理和对称山路定理研究问题(**)超线性情况下有无穷多个高能量解,为了克服Sobolev 嵌入紧性缺失的情况,他们假设V(x)满足 (V′)V∈C(N,),满足其中a1>0为常数. 而且,对于任何M>0,meas{x∈N,V(x)≤M}<∞,其中meas(·)为在N中的勒贝格测度.

随后,在条件(V′)下,Ye和Tang[9]获得了无穷多个高能量解和低能量解,从而对文献[8]中的结果得到了进一步的推广. 最近,Avci, et al.[2]通过利用变分方法以及截断方法研究如下问题

得到了至少有一个正解.

综上可知,四阶非局部基尔霍夫问题的正解、高能量解、低能量解的存在性已得到广泛、深入的研究,但是关于四阶非局部基尔霍夫问题的山路解以及基态解的结果很少. 受以上文献启发,本文利用山路定理研究问题(*)的山路解以及基态解. 对V(x)以及q(x)作如下假设,其中a,b>0为常数,

(A)q(x)>0为连续函数且存在R0>0,使得

(V)V∈C(3,)满足且存在使得

对f(x,u)作如下假设,

(f1) 对任意的x∈3,有一致成立.

(f3) 对所有的x∈3,存在d0满足使得成立,其中u∈且S2由(2.1)定义.

对于V(x),条件(V′)是一个经典的限制条件用来确保嵌入的紧性. 在文献[1]中,Bartsch 和Wang证实了以上限制条件(V)弱于(V′). 当然,在文献[7] 中仍然有其他方法确保紧性条件成立. 在这篇论文中,我们使用比(V′)更弱的条件(V)来获得嵌入的紧性.

1 主要结果

本文的研究主要结果如下.

定理1.1 假设(f1)-(f3),(V)和(A)成立,若l>μ,其中

(ⅱ)问题(*)至少有一个基态解.

与已有文献工作相比较，本文的工作的新颖之处主要体现在以下两方面.

(2)用q(x)f(x,u)来代替通常的非线性项f(x,u),形式上较为复杂,这使得对于验证泛函的山路几何结构有一定的困难. 大多数文章用变分方法以及截断方法研究四阶非局部基尔霍夫问题的正解、高能量解、低能量解,极少有文章研究此类方程的基态解以及山路解. 因此,本文的工作是对已有四阶非局部基尔霍夫问题研究的有益的补充和推广.

本文结构如下,第2节给出必要的预备知识和变分框架,第3节给出相关引理以及主要定理的证明.

2 预备知识和变分框架

本文采用如下记号. 定义Sobolev空间

H:=H2(3):={u∈L2(3):∇u,Δu∈L2(3)},

内积以及范数分别为

工作空间为

内积和范数分别为

|u|p≤Sp‖u‖,∀u∈E.

(2.1)

(2.2)

在已有条件下可得Ib∈C1(E,),并且对于任意的u,v∈E,有

(2.3)

定义2.2 设E为巴拿赫空间,E*为E的对偶空间,如果对任意的序列{un},I(un)→c,I′(un)→0,序列{un}都有一个收敛子列,则称泛函I满足(PS)c条件.

引理2.3 设E为实的巴拿赫空间,假设I∈C1(E,),使得对某个α<η,ρ>0,e∈E且‖e‖>ρ,有成立. 设且则存在序列{un}⊂E,使得当n→∞时,有且I′(un)→0.

3 定理的证明

首先证明下列引理.

引理3.1 假设(f1)-(f3),(V)以及(A)成立,则

(ⅰ)存在ρ>0,α>0,使得对所有的u∈E,且‖u‖=ρ,有Ib(u)≥α>0.

证明(ⅰ) 由条件(f1)和(f2)知,对任意的ε>0,存在p>1和C=C(ε)>0使得

f(x,u)≤ε|u|+C|u|p,∀x∈3,

(3.1)

则有

(3.2)

其中A=A(ε,p)>0. 而且,由(f1)-(f3) 以及(A) 知,存在C1>0使得

q(x)≤C1,∀x∈3.

(3.3)

因此,由(3.2)和(3.3) 知,对任意的u∈E,有

取e=t0u且t0足够大,因此I0(e)=I0(t0u)<0,且‖e‖=t0‖u‖>ρ.

对于引理3.1给出的α和e,根据引理2.3知,存在(PS)序列{un}⊂E使得

(3.4)

引理3.2 假设(V),(f1)-(f3)和(A)成立,则由(3.1)定义的{un}有一个收敛的子序列.

证明对于足够大的n,由(f3),(2.2)以及(2.3)知

以上讨论得出了{un}的有界性. 接下来,证明序列{un}有一个收敛的子序列. 仍把子列记为{un},假设un⇀u在E中,un→u在Ls(3)中,其中2≤s<6,un→u几乎处处在3中,则

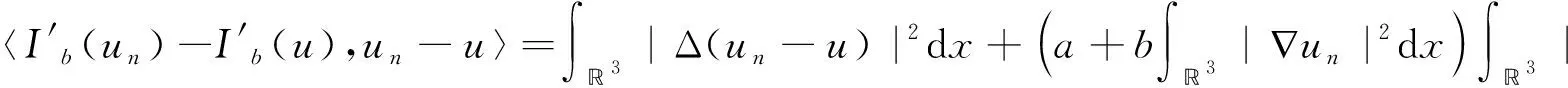
通过计算可得

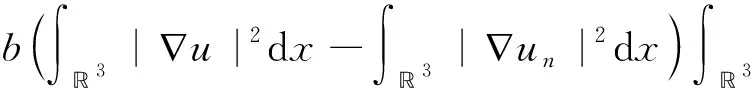
因为

εC2|un-u|2+C3C1|un-u|p+1→0,n→∞.

显然,由于当n→∞时,有I′b(un)→0,所以有n→∞时,得出〈I′b(un)-I′b(u),un-u〉→0,所以当n→∞时,有‖un-u‖E→0成立. 证毕.

定理1.1的证明(ⅰ) 由引理3.1,3.2以及引理2.3可证得此结果.

(ⅱ)为了获得基态解,用K表示Ib的非平凡临界点集. 设m=inf{Ib(u):u∈K},很容易得出K为非空的. 对于任何u∈K,有

因此,对于任意的u∈K,有

0≥‖u‖2-εC1S2‖u‖2-CC1Sp+1‖u‖p+1.

(3.5)

由于对任意的u∈K,均有u≠0,则由(3.5)知,对任意的u∈K,有

(3.6)

因此,在K中,序列的任何极限点均非零.

我们断言Ib在K中下方有界. 也就是说,对所有的u∈K,存在M>0,使得Ib(u)≥-M. 否则,对任意的n∈,存在{un}⊂K使得Ib(un)<-n.由3.1(ⅰ)知结合Ib(un)<-n,这意味着当n→∞时,有 ‖un‖→+∞. 正如引理3.2的证明,我们知道‖un‖→+∞是不可能的. 则Ib在K中是下方有界的. 因此m≥-M. 设使得当n→∞时,有则对于序列以及实数m,(3.4)式成立. 下面的步骤与引理3.2中的证明相似,我们可以得出在H中是有界的,把其子列仍记为且有其中而且以及因此,为问题(*)的基态解. 证毕.