基于灰狼粒子群混合算法的相机标定优化方法

王道累， 柴萍萍*， 孙 昊， 胡 松， 韩 洋

(1.上海电力大学能源与机械工程学院， 上海 200090； 2.中国电建集团江西省电力设计院有限公司， 南昌 330096)

日新月异的计算机技术和传感器技术也推动了无人驾驶、机器人定位导航、三维重建等相关领域的发展[1-3]。其中，标定是一个基础而重要的环节，提高标定的精度是非常有必要的。目前，广泛应用并接受的标定方法有两种：传统校准法和自校准方法。根据计算方法不同，传统标定法主要包括直接线性方法[4]、基于径向排列约束(radial alignment constraint, RAC)的两步标定法[5]和张正友标定法[6]等。直接线性变换法是将摄像机模型看作是线性的，这和实际情况不符，后经过改进引入非线性畸变因素。基于RAC 的两步标定法利用相机成像模型中的一部分内在性质和关系先求解出一些参数， 然后利用这些已求出的参数增加相机非线性畸变等因素对模型进行优化，这使得求解过程中大多是线性方程，计算简单，结果准确。在2000年，一种里程碑式的方法由张正友提出，基于二维的棋盘格进行标定。该方法在两步标定法的基础上改进标定物，用最大似然法求解各个参数。由于借助的外物成本低廉、易操作、标定精度较高等优点，这种方法被广泛使用，但对精度的提高仍有局限性。

为了弥补这些方法的不足，中外学者在优化求解算法和标定物改进两个方向做了各种研究。傅思勇等[7]提出一种新的两步标定法，首先求解初始参数，后综合考虑前二阶径向畸变、前二阶切向畸变和薄棱镜畸变，建立多畸变模型后迭代逼近求解，在噪声的情况下仍能保持较小的误差。向鹏等[8]提出基于深度学习的标定方法，利用改进DNN网络逼近能力，输入原始图像的坐标即能实现标定，在大范围、多拍摄角度等复杂环境都适用，但深度学习网络训练需要GPU加速，对电脑配置要求高，且训练需要时间，不能快速标定。雷阳等[9]将粒子群算法和模拟退火算法结合得到混合算法，先用最小二乘法求得初始参数，再用混合算法优化，此法有提高标定的精度。Jiang等[10]改进标定物，利用液晶板进行操作，在液晶板上生成一系列不同角度的标定图像，无需人工操作，结果精度高，但相对于棋盘格而言，液晶板增加了成本。

沿用棋盘格标定，改进优化算法，提出一种基于灰狼和粒子群优化的混合算法，改善粒子群算法易早熟的缺点，将该方法首次应用到摄像机标定上，与几种方法比较后明显看出提高了标定的精度，且标定的结果稳定可靠。

1 摄像机成像模型

摄像机成像模型主要反映相机把真实3D世界拍摄成图片的过程，其可简单看作是小孔成像模型[11]。即其是一个线性模型，如图1所示。成像涉及4个坐标系，即世界、相机、图像和像素坐标系之间按一定规律进行变换。

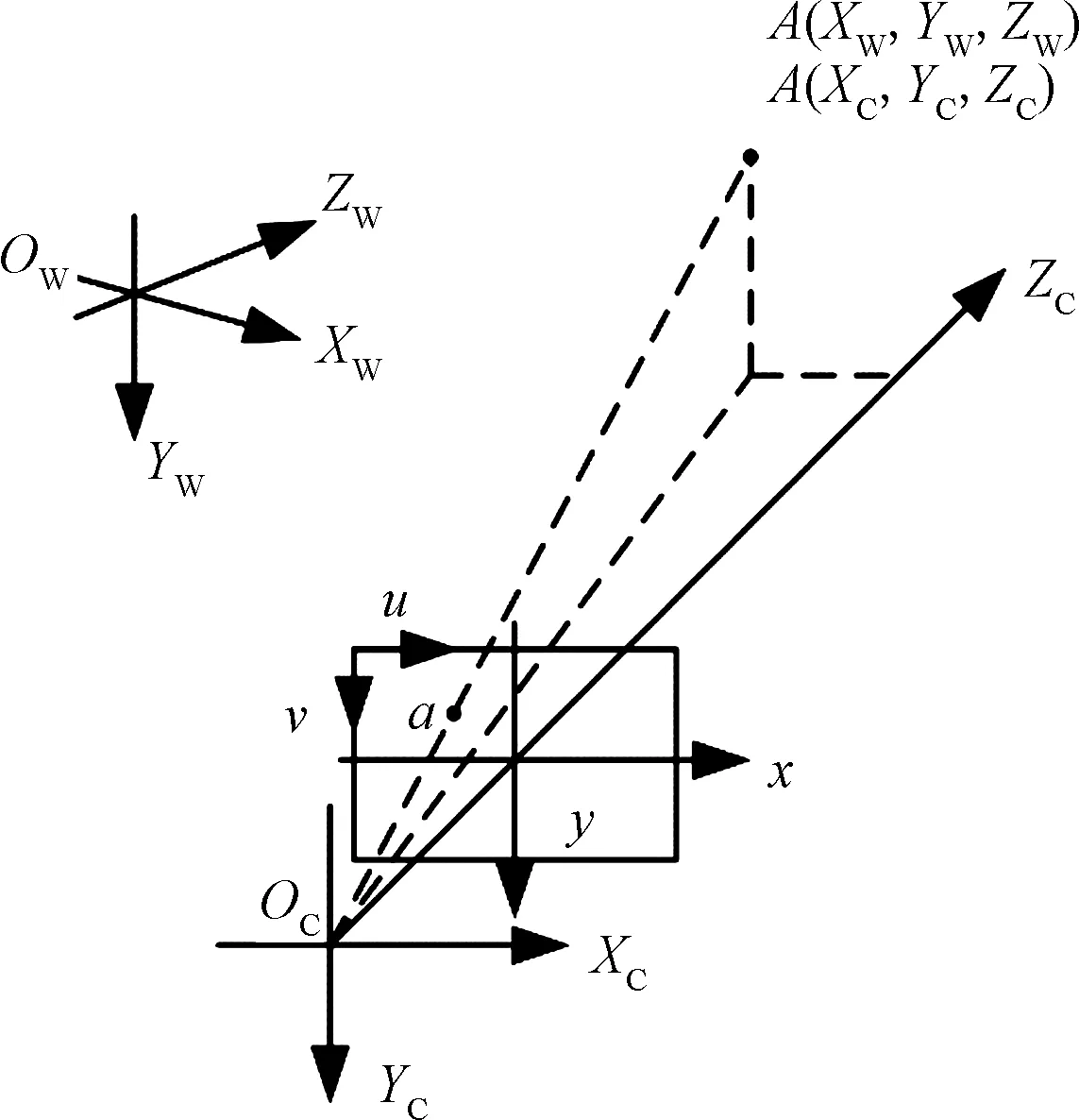
(XW,YW,ZW)为世界坐标系；(XC,YC,ZW)为相机坐标系；(x,y)为图像坐标系;(u,v)为像素坐标图1 单目摄像机模型Fig. 1 Monocular camera model

(1)世界坐标系(XW,YW,ZW)：或者可以称作测量坐标系，是一个正交的三维3D直角坐标系，以现实中存在的某一物体为标准建立。

(2)相机坐标系(XC,YC,ZC)：同样是一个3D直角正交坐标系，原点在镜头光心，镜头光轴即是Z轴。

假设现实中三维空间中有一点A，其在世界坐标系中坐标为(XWA,YWA,ZWA),那通过式(1)可以得到点A在相机坐标系中的坐标(XCA,YCA,ZCA)：

(1)

式(1)中：R和T分别为旋转矩阵和平移向量。

(3)图像坐标系(x,y)：建立在成像平面上的一个2D直角坐标系，和上一个坐标系之间的转换被叫作透视变换，用几何中的相似三角形知识就能求解，求解公式为

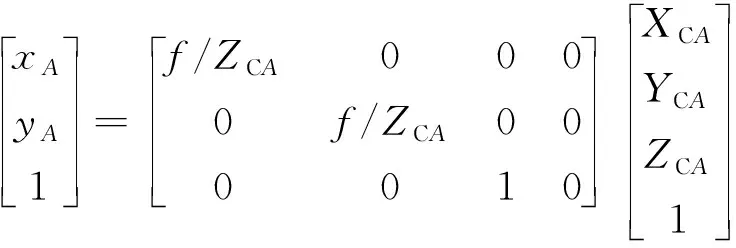
(2)

式(2)中：f为相机的焦距；XCA、YCA、ZCA分别为相机坐标系下点A的X、Y、Z轴方向上的坐标。

(4)像素坐标系(u,v)：和图像坐标系建立在同一平面上，但区别在两者的原点位置不一样。之间的变换关系，可以描述为

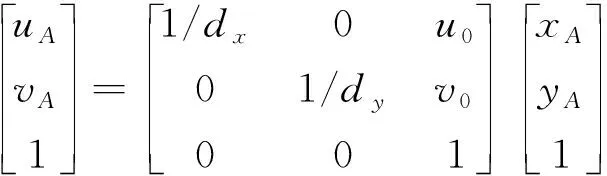
(3)

式(3)中：(u0,v0)为两坐标轴交点即原点O的坐标；dx、dy表示两坐标轴上单位像素的物理大小。

实际的应用场景中，由于生产制造技术限制、安装位置不理想等因素影响，硬件摄像机拍摄结果会存在非线性的畸变，这也是误差的主要来源[12]。文献[13]指出主要畸变分为偏心、径向、薄棱镜畸变3种。综合作用下，在径向和切向两个方向上都会存在误差，误差计算公式为

(4)

式(4)中：k1、k2、p1、p2、k35个变量就是在两个方向上与误差相关的因数。

2 灰狼粒子群混合算法

2.1 标准粒子群算法

粒子群算法(particle swarm optimization，PSO)是1995年提出的一种仿生算法，来源于鸟群捕食[14]。每个粒子在寻优过程中如同鸟群中的一只鸟，既可互相交换信息，又有记忆。从每个粒子位置中选出pbest(个体最优位置)，并将每次搜索出的pbest作为gbest(全局最优位置)更新的基础。假设粒子i在dim维空间内搜索求解，它的飞行位置xi=(xi,1,xi,2，…，xi,dim),速度vi=(vi,1,vi,2，…，vi,dim)。 该算法的位置和速度计算公式为

(5)

式(5)中：k表示目前是第k次迭代；w为惯性因数；c1、c2分别为个人和社会学习系数；r1、r2为一对(0,1)范围内互不干扰的随机数。

2.2 灰狼算法

灰狼优化(grey wolf optimization，GWO)算法是一种新的仿生算法，提出时间较晚，由Mirjalili在2014年给出，灵感来自狼群捕食活动。狼群中的社会支配关系犹如金字塔形，被划分成4个等级。在金字塔顶端的是α狼，拥有绝对的领导权，次之是β狼，在β狼下面的是δ狼，最低的是ω狼。其中，β狼服从α狼，δ狼服从于α狼和β狼，在金字塔底端的ω狼受其余3种狼的支配。在头狼α的领导下，狼群分工合作，搜寻、围捕和攻击猎物[15]。类似于灰狼的社会形态组成，将求解得到的最优解、次优解、季优解和一般解看作狼群中的4个等级。寻优过程可看作是狼群追捕猎物过程。

包围的具体公式为

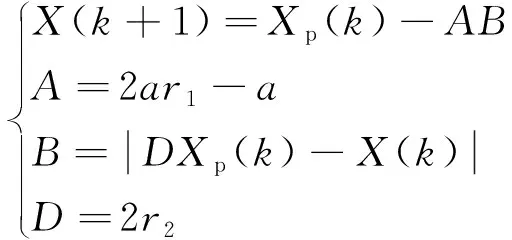
(6)

式(6)中：Xp(k)、X(k)分别表示在第k次寻优后猎物和灰狼的位置；a为控制系数；A、B、D为系数因子；r1、r2为(0,1)范围内互不干扰的随机数。

包围猎物后，狼群在头狼带领下追捕猎物，猎物的位置随着逃跑也会改变，此时，狼群的位置随之改变，计算公式为

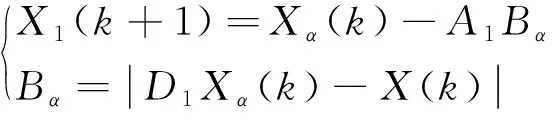
(7)

(8)

(9)

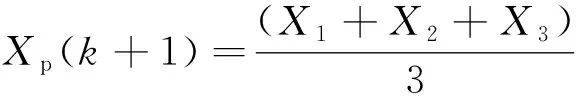
(10)

式中：Bα、Bβ、Bδ分别表示α狼、β狼、δ狼和其余狼之间的距离。

2.3 灰狼粒子群混合算法

粒子群收敛快但鲁棒性弱，而灰狼算法正好相反，将两个算法的优点融合到一起即为灰狼粒子群混合算法[16]。灰狼粒子群混合算法主要是两个算法嵌套使用，主循环为粒子群算法，次循环为灰狼算法，在每次主循环完成一次，将得到的gbest引导次循环中的头狼追捕猎物，公式为

Xα(k+1)=gbest(k)

(11)

为了防止主循环中的粒子群陷入局部收敛，对其速度公式进行优化，将次循环后得到的头狼位置Xi,dim(α)也参与速度的计算，速度公式更新为

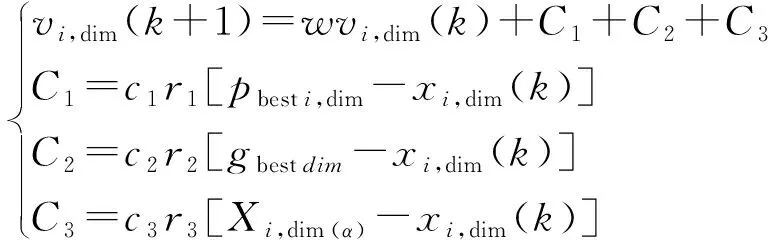
(12)

式(12)中：w采用的非线性变化策略，初始的阶段w值大，搜索能力强，到接近最优解附近，w值缩小，开启细致小步长搜索，w的更新公式为

(13)

式(13)中：w1、w2分别为惯性因数最大和小值；k为当前迭代系数；itermax为最大迭代次数。

具体描述如下：

(1)在上下限范围内随机生成种群位置X，初始化速度v，并给定最大迭代次数itermax，种群维度dim，种群数量n，学习率c1、c2、c3和惯性因数等参数。

(2)为了使适应度函数最小(或最大)，根据灰狼算法产生最优解、次优解和季优解，迭代L次后，返回最优解的位置并跳出该循环。

(3)使适应度函数最小(或最大)，分别根据式(13)、式(12)和式(5)重新计算速度和位置，每次循环后更新pbest和gbest的值，最后返回gbest的相关参数。

(4)如果在没达到迭代停止条件的情况下，根据式(11)更新头狼位置，然后从第2步开始计算，完成次循环后进行第3步。直到达到终止条件，此时，输出内外参数和最小误差值。

3 实验与结果分析

3.1 标定实验

实验的硬件平台是一台采用索尼ICX445传感器的数字摄像机，来自德国AVT公司。在全分辨率1 624×1 234下，该Manta工业数字摄像机帧率可达30 fps。采用8行11列的激光打印的标定板，单个格子的尺寸为20 mm×20 mm，以棋盘格角点作为标定点，共计88个角点。软件平台是在PYTHON上进行数据处理。一共拍摄16张照片，部分图片如图2所示。

图2 摄像机标定拍摄的部分图片Fig.2 Pictures of camera calibration

具体步骤如下：

步骤1用PYTHON-OPENCV可以得到图像中的实际的像素坐标(x,y)。

步骤2根据张正友方法得到的参数为基础，确定迭代上下界。为了避免寻优范围太大造成收敛慢，将得到的内参数(fx,fy,u0,v0)±80，畸变系数(k1,k2,p1,p2,k3)±10作为寻优的上界和下界。设置粒子群粒子数量为80，w1为1.4，w2为0.3，学习率c1、c2、c3分别为1.9、1.3、0.3，次循环的灰狼算法中灰狼数量是25，运行20次，主循环是运行400次。建立目标函数δ，即实际坐标(x,y)，与优化后反投影得到的(x′,y′)之间误差的平均值，公式为

(14)

式(14)中；N表示标定的角点个数；pj代表角点j的实际像素坐标；p′j代表角点j的反投影坐标；A表示摄像机内参矩阵。

步骤3在上下界之间随机生成初始值，初始值为9维。

步骤4先在次循环中用灰狼算法寻优，经过20次迭代以获得头狼的最佳位置，紧接着更新粒子群粒子的速度和位置，计算pbest_δ。

步骤5更新pbest_δ，判断当前得到的pbest_δ是否小于上一次迭代得到的pbest_δ，若是，就更新pbest_δ。否则，保留上一次迭代结果。

步骤6更新gbest，使得gbest_δ=min(pbest_δ)，并回到步骤3继续执行，直到迭代结束。

步骤7输出全局最优解。

3.2 实验结果与分析

图3给出了基于灰狼粒子群混合算法在400次循环迭代过程中目标函数的变化情况。从图3可知，初始目标函数值达到1.38左右。这是因为初始位置是在给定的上下界随机生成的，所以此时误差会较大。在开始到50次，曲线肉眼可见地下降很快。这是由于大的惯性因数带来非常强的寻优能力，收敛非常快。在50～150次，下降变得非常平缓，目标函数值仍在减小。这个阶段是在前期已获得较优解附近，更细致小范围地寻找最优解，即局部寻优。在约200次后图像基本不动，说明此时已经求解到最优目标值。进一步提取详细参数和结果进行分析。

图3 目标函数曲线Fig.3 Curve graph of objective function value

表1所示为基于混合算法求解出的相机标定内部参数和畸变系数以及目标函数值，分别给出了迭代50、100、150、200、300、400次后的结果。从表1可知，在初始阶段，算法快速收敛，目标函数值从刚开始的1.378像素值下降到了0.073像素值，下降了1.305像素值。在50次到150次时，下降了0.054像素值。在循环了150次但未到达200次时，反投影平均误差略有减小。达到200次后，目标函数值稳定不变。

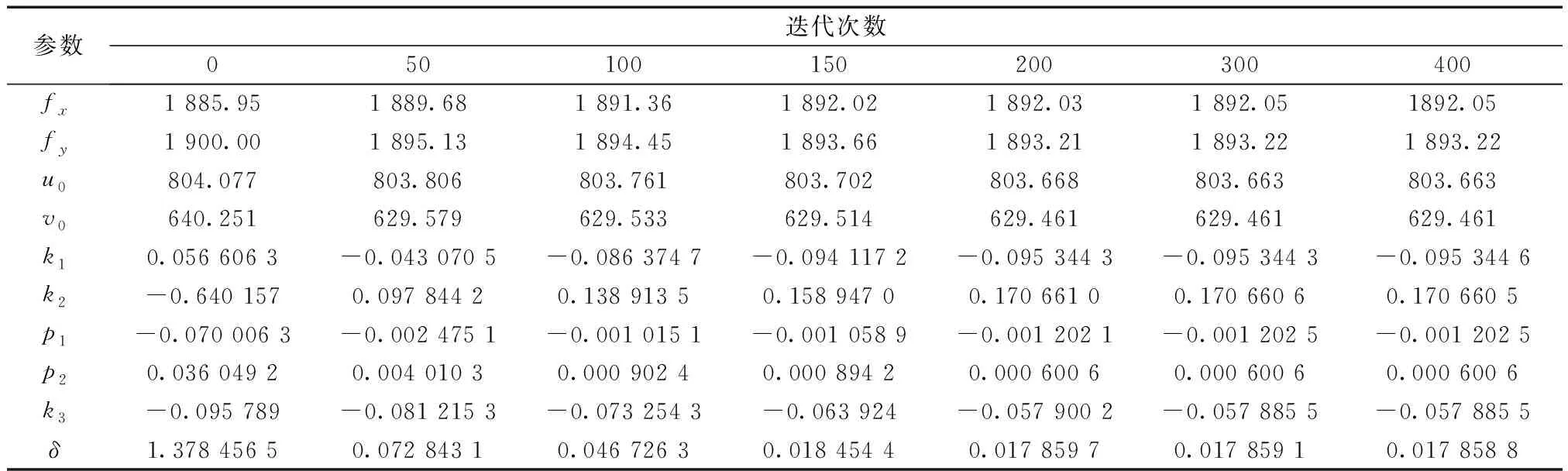
表1 基于混合粒子群算法标定算法的结果

为了验证混合算法的精准性，分别计算了张正友方法、标准粒子群算法、标准灰狼算法和本文算法标定后的各参数和重投影平均误差。表2给出来了4种计算方法的标定结果。其中，本文算法摄像机标定的平均误差是0.017 86像素值，优于张正友方法的0.211 34像素值，同样小于粒子群算法的0.085 15像素值和灰狼算法的0.062 12像素值。

通过两个试验对比，来检验本文算法是否稳定。每个试验会采用不一样的标定板，除此之外，其他条件都相同。第1个试验使用前文的标定板(board1)采集图片，分为3组，每组图片数量依次为10、20、30张。第2个试验换规格为11×8，格子大小为15 mm×15 mm的标定板(board2)重复上述操作。采用前面提到的4种方法进行实验，即每个标定方法都会进行标定板1(board1)和标定板2(board2)的共计6组标定试验。记录每组的反投影平均误差，最后计算3组实验反投影误差的平均值，试验结果如表3所示。

从表3可看出，在第1个实验中，即标定板用的是前文提到的board1的情况下,张正友标定法得到误差的平均值是0.210 88像素值，标准粒子群算法得到误差的平均值是0.081 42像素值，灰狼算法得到误差的平均值是0.061 19像素值，本文算法得到误差的平均值是0.017 75像素值，优于其他3种方法。在第2个试验中，将标定板换为board2，同样每种方法进行3组试验。张正友标定法得到误差的平均值是0.163 12像素值，标定标准粒子群和灰狼算法的误差平均值分别为0.031 24像素值和0.059 73像素值，本文算法是0.015 90像素值，本文算法得到的误差更小。综合两个试验来看，本文算法不管是在标定板改变的情况下还是图片数量改变的情况下，目标函数值依然是4种方法里面最小，且数值波动不大。综上可看出，本文算法鲁棒性强，可重复使用。

表2 不同算法结果

表3 可重复性试验结果

4 结论

以粒子群和灰狼算法为基础进行研究，将标准粒子群算法部分进行改进，引入非线性惯性系数，再与标准灰狼算法按一定机制融合两者到一个框架中，有效提高标定的精确度。将本文算法与其他同类方法比较，经试验验证，该标定方法可重复使用，具有良好的稳定性和准确性。在求解过程中，首先建立非线性标定模型，通过张正友方法获得标定的上下限范围，初始迭代时在上下限范围内随机生成粒子位置，以目标函数最小为目的进行迭代计算。该算法可以与实际工程案例结合，能准确、有效地用于多维非线性问题优化求解。