恒定磁场下的磁性液滴变形数值模拟
2021-04-22卢银彬梁辰伟
卢银彬, 梁辰伟
(西安石油大学机械工程学院,西安 710065)
磁流体,又称为磁液或铁流体,是21世纪60年代早期发现的一种液态磁性材料,该材料在外加磁场作用下流变特性发生急剧变化[1]。磁流体的基本组分为磁性微粒(平均直径不大于10 nm)、基液(也叫载液)和表面活性剂,是包含磁性纳米颗粒的稳定胶体悬浮液。通常在磁性颗粒表面涂有表面活性剂,分散在非磁性载体基液中[2]。磁流体在无外加电磁场作用下呈流动性良好的液体状态,然而在外加磁场作用下流变特性急剧变化并呈现类似固体的力学性质,而一旦去掉磁场后又变成可以流动的液体,这些特点引起了中外学者和工业界的广泛兴趣,成为材料及控制领域研究的热点之一[3-8]。目前,由于工业技术的进步,磁流体已被广泛地运用到生物、医疗和化学分析等多个领域[9-14]。
磁液滴是在含有表面活性剂的液滴中添加少量纳米量级尺寸的铁颗粒[2]。现代科技拥有许多技术操控磁液滴,主要有化学梯度、热毛细管现象和电泳等[15-17]。此外,对磁液滴施加外部磁场也是有效控制液滴运动的无触点方式之一。当将磁液滴放置到另一种具有不同磁性的流体内,并将两种液体暴露在磁场中,磁液滴会发生运动变形行为。中外科学界和工业界关于磁场对磁液滴运动影响方面的研究已相继展开。Flament等[18]实验研究磁液滴在恒定磁场中的Hele-Shaw盒子中的形态。研究结果表明:Hele-Shaw盒子中磁液滴沿磁场方向延长。Capobianchi等[19]数值模拟研究磁流体液滴在剪切流中受到磁场作用的运动行为。研究发现,液滴的变形和倾角随毛细数的变化而变化,当毛细数非常小时,磁液滴的变形随时间变化呈现类似简单阻尼谐振子特性。陈芳等[20]制备出尺寸2.0~4.0 mm的油基磁性液滴,观察分析不施加磁场或施加换向频率为0~100 Hz的磁场时磁性液滴的不稳定性现象,研究指出:磁性液滴在永磁铁作用下汇聚成椭球型,移除永磁铁后可较长时间内形状保持不变;当磁场换向频率为0 Hz时,磁性液滴沿磁场方向迅速移动;磁场换向频率0 关于磁液滴在磁场中的运动变形的深入研究尚鲜见报道,对磁液滴变形机理需要进一步分析明确,亟需对磁性液滴的变形机制展开深入研究。为此,以商业数值软件Fluent为工具,模拟研究恒定磁场空间内磁性液滴的变形情况,旨在提出磁液滴受磁场影响的作用规律,为工程领域制定合理控制磁液滴运动策略提供理论依据。 对悬浮于空气中的磁液滴施加外部磁场,分析磁液滴变形规律。模拟磁液滴直径d= 1.0~4.0 mm。液滴的磁导率μ=0.001 257 H/m,密度ρ=998 kg/m3,黏度η=0.001 003 Pa·s,空气与磁液滴之间的界面张力σ=70 mN/m。 采用计算模型的几何尺寸为20 mm×15 mm。采用Gambit对网格进行划分,由于计算区域与液滴尺寸相差较大,故仅展示计算局部区域网格情况,如图1所示。磁液滴采用非结构化网格(中间圆形区域),其余计算区域采用结构化网格。 图1 直径2 mm液滴的网格Fig.1 Mesh of 2.0 mm diameter droplet (1)质量守恒方程,又称连续性方程: ∇·(ρu)=0 (1) 式(1)中:ρ为流体密度,kg/m3;u为流速,m/s。 (2)动量守恒方程: (2) 式(2)中:p为流体压力,Pa;η为流体动力黏度,Pa·s;σ为界面张力,N/m;k、n分别为界面曲率和垂直于界面的单位向量;δ为界面上的分布函数;μ0为真空磁导率,μ0=1.257×10-7H/m;M为流体磁化强度,A/m;H为磁场强度,A/m。 磁场力和界面张力占主导作用,故忽略重力的影响[19]。根据麦克斯韦电磁理论,对于绝缘磁液滴来说,其磁通密度(B)和磁场强度(H)满足: ∇·B=0 (3) ∇×H=0 (4) 对于磁液滴,有 B=μ0(H+M) (5) 对围绕在磁液滴周围流体,有 B=μ0H (6) (3)两相模型。采用volume of fluid(VOF)模型,以体积分数(φ)描述计算区域的流体相。对于任意某计算节点处,均有 φair+φdroplet=1 (7) 式(7)中:φair为空气的体积分数;φdroplet为磁液滴的体积分数。当φair=1或φdroplet=0表示该计算节点控制区域为空气,当φair=0或φdroplet=1表示该计算节点控制区域为磁液滴,当φ值介于两者之间时为气液两相过渡区域。 对于任意计算节点处的流体密度(ρ)和黏度(η),其表达式分别为 ρ=φairρair+φdropletρdroplet (8) η=φairηair+φdropletηdroplet (9) 采用无滑移壁面条件,出口(顶部)采用压力出口条件。在横向维度对液滴施加恒定磁场。 为证明模拟结论的有效性,将文献[21]中液滴在疏水性表面上受磁场力作用下的液滴高度(hd)与模拟数据进行对比,如图2所示。从图2可以看出,模拟数据与实验点吻合,证明本研究模拟的准确度性。 图2 模拟数据点与文献[21]对比Fig.2 Comparison of numerical data with available data of literature[21] 图3~图5分别为直径1、2、3 mm的磁液滴受磁场作用下的相云图情况。 图3 直径d=1 mm的磁液滴Fig.3 Droplet with diameter 1 mm 图4 直径d=2 mm的磁液滴Fig.4 Droplet with diameter 2 mm 图5 直径d=3 mm的磁液滴Fig.5 Droplet with diameter 3 mm 横向对比图3~图5可以看出,随着磁通密度的增加,液滴越容易发生变形,而且磁液滴变形时间也随着磁通密度的增加而缩短。纵向对比图3~图5,即图3(a)、图4(a)和图5(a)对比(其他分图类似),可以发现当液滴尺寸增大时,施加可让磁液滴产生变形的磁通密度也随之降低。 为明确磁液滴尺寸与磁通密度之间内在联系,模拟一系列数据点考查是否存在某一个临界磁通密度,即最小磁通密度,能够使磁液滴发生变形。图6所示的模拟数据点为不同尺寸磁液滴发生变形的临界磁通密度。 图6 液滴尺寸与临界磁通密度的关系Fig.6 Relationship between diameter and critical magnetic induction intensity 从图6可以看出,随着磁液滴尺寸的增加,需要让其发生变形的临界磁通密度越小,即磁液滴尺寸越大,越容易受到磁场影响而发生变形。将不同尺寸磁液滴发生变形时的临界磁通密度进行分析并拟合,得到磁液滴尺寸和临界磁通密度之间的关系满足: Bcr=(530/d)-98 (10) 式(10)中:Bcr为临界磁通密度,mT;d为液滴直径,mm。 从式(10)分析可知,当磁液滴尺寸越小时,临界磁通密度越大,若d→0,意味着磁液滴尺寸无限小,无论施加多大强度的磁通密度都无法实现磁液滴的变形。这是因为,磁液滴尺寸越小,其比表面积越大,维持磁液滴球状的能量,即表面能越大,若要磁液滴发生变形,需要更大的外界能量。当磁液滴直径接近0时,可认为需要的外界能量也趋于无限大;当d=5.4 mm,B=0,这意味着当磁液滴直径达到5.4 mm以上时,无需磁场作用,磁液滴本身就很难保持稳定存在。实际上,在生产生活中,由于磁液滴表面张力的作用,在无外界能量维系的情形下,磁液滴尺寸也是极难达到该数值[22]。 采用商业数值软件Fluent模拟研究磁液滴在恒定磁场中的运动情况。模拟考虑磁液滴在空气中处于悬浮状态时,受到水平方向恒定磁场的作用,进而发生运动变形。研究采用的磁液滴尺寸为1.0~4.0 mm。研究得出如下主要结论。 (1)磁液滴受磁场影响随着磁通密度的增大而增大,主要体现为磁液滴更容易发生变形运动行为。 (2)磁液滴尺寸越大,越容易受到磁场的影响发生变形,即此磁液滴发生变形的临界磁通密度Bcr越小,临界磁通密度Bcr与磁液滴直径d符合Bcr=(530/d)-98的函数关系。 (3)当磁液滴尺寸无限小,施加磁通密度的大小与否均无法获得磁液滴的变形;并且,当磁液滴直径达到5.4 mm以上时,即便无磁场作用,在无外界能量干扰的前提下,磁液滴本身也很难稳定地存在。1 建模

2 磁液滴在磁场中运动的物理模型

3 结果与讨论
3.1 模拟有效性验证
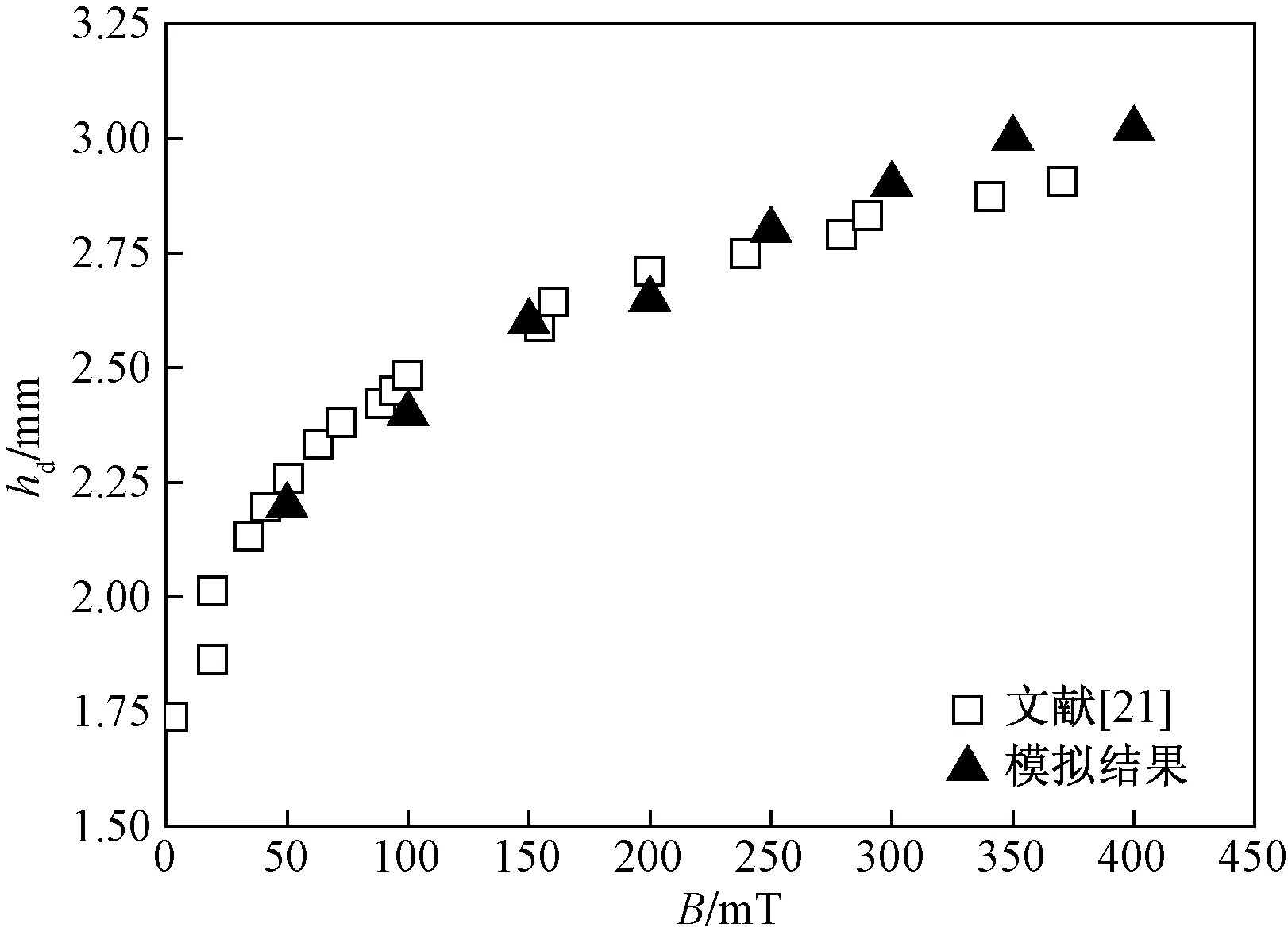
3.2 磁液滴在恒定磁场下的变形


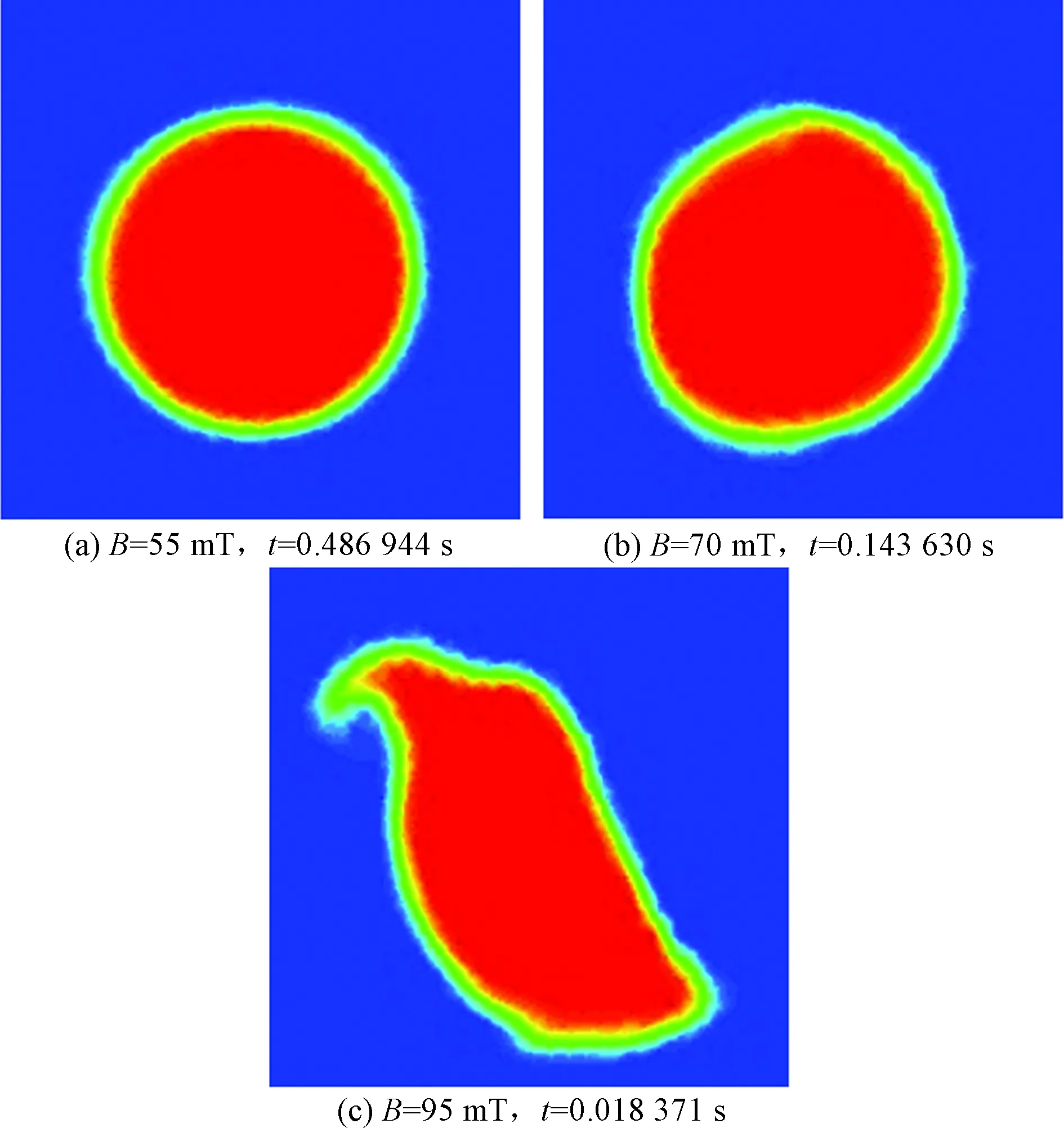
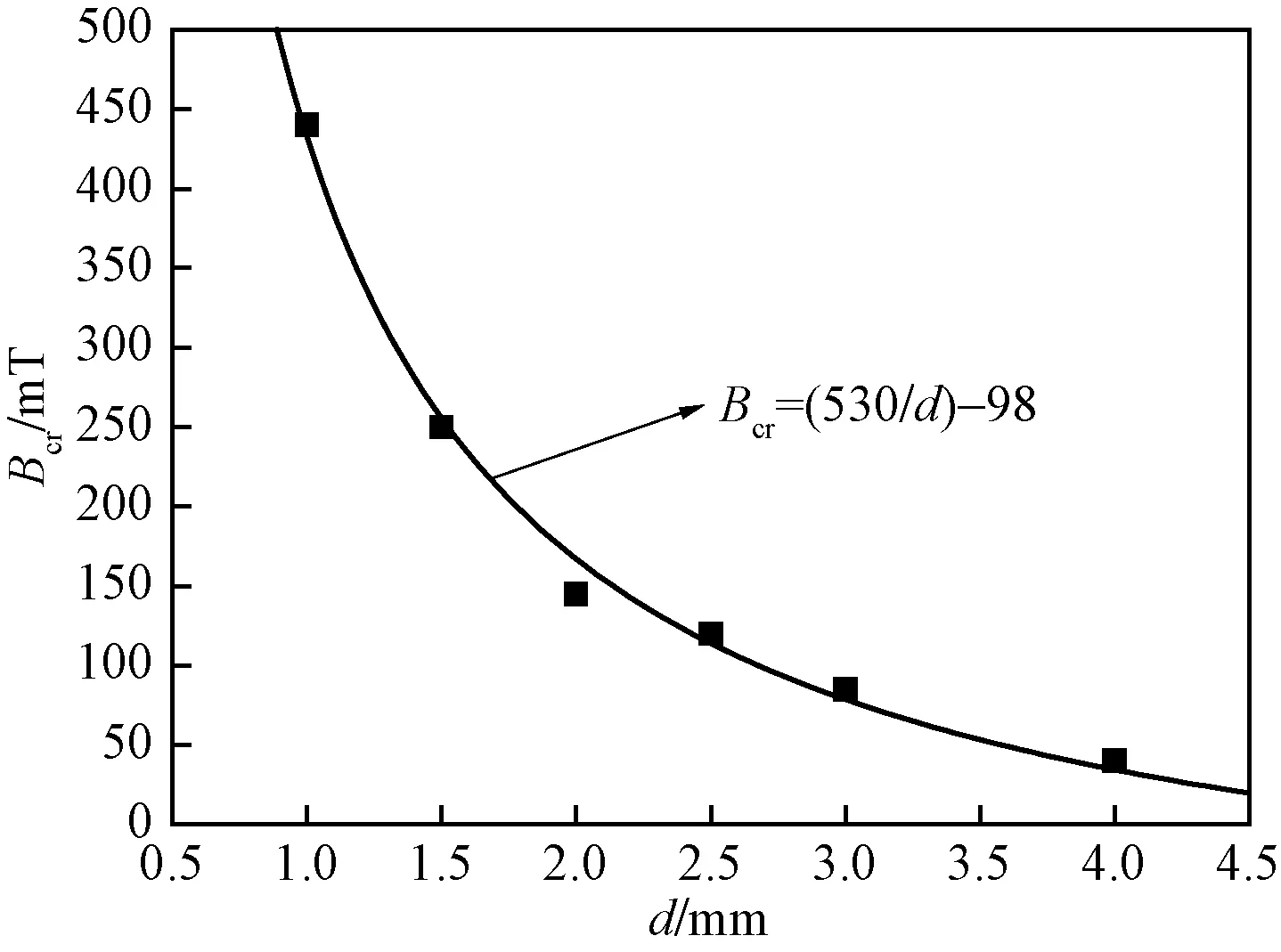
4 结论
