三时间尺度下非光滑电路中的簇发振荡及机理1)
2021-04-22毛卫红张正娣张苏珍
毛卫红 张正娣 张苏珍
(江苏大学数学科学学院,江苏镇江 212013)
引言
多时间尺度问题[1-2]作为非线性科学的重要组成部分广泛存在于物理学、化学、生物学等领域中.例如在生物细胞的遗传中,由较快的新陈代谢过程与相对较慢的遗传变化过程的结合导致的快慢耦合[3];在催化反应中,不同量级反应速率之间的催化与自催化过程[4];在神经动力学中,静息态和激发态交替出现的簇放电模式[5]等.相比于单一时间尺度的系统,多时间尺度耦合系统会表现出更为特殊的动力学行为,例如周期振荡中通常表现出的大幅振荡和微幅振荡的复合振荡[6-7].大幅振荡和微幅振荡可以分别看作快慢系统的激发态(spiking state)和沉寂态(quiescent state).这种连接快慢两个过程的行为也称为簇发(bursting)[8-10],通常是由分岔产生的[11-12],可以得到“点点”型簇发振荡、“点环”型簇发振荡等.这类具有特殊结构的系统往往表现为复杂的动力学行为,例如混沌簇发振荡[13],吸引着国内外学者的关注,尤其是在Izhikevich 等[14-16]引入Rinzel 的快慢分析理论后,对于含多时间尺度的非线性动力系统,许多学者从数值仿真、理论分析、数值实验等方面进行了深入的探索[17-20].
非光滑动力系统具有广泛的工程背景,涉及到科学和工程技术的各个领域.不同于光滑系统的分岔现象,非光滑系统不仅可以产生光滑系统中的各种常规分岔,而且还可能发生一些光滑系统所不具备的特有分岔,统称为非光滑分岔[21].例如,非光滑滑动分岔、擦边分岔、角点碰撞分岔等[22-25],导致系统产生复杂的振荡行为,对系统的动力学行为产生重要的影响,从而提供了更多通向混沌的路径,并且其研究方法与光滑系统也不尽相同[26-27],是非光滑动力学研究的热点和难点.
目前,对含多时间尺度非线性动力学行为的研究主要针对只含有一个慢变过程的快慢两尺度系统[28-29],对于含有两个或两个以上慢变过程的、含3 个及以上时间尺度的非光滑系统,关于其沉寂态与激发态相互转迁而导致簇发振荡的非光滑分岔模式的研究相对较少,而根据实际问题建立的动力系统通常含有不止两尺度.
本文工作如下:基于典型的非光滑蔡氏电路,通过选取适当的参数值,建立了一个含三时间尺度的四维分段线性电路系统模型.通过重新划分系统的快慢子系统,将三时间尺度耦合问题转化为两时间尺度耦合问题.分析了快子系统的动力学行为,给出了不同参数下系统存在的两种典型的簇发振荡行为.结合转换相图,利用快慢分析法研究了系统的簇发振荡现象以及三尺度之间的相互作用机制,探究了非常规分岔在多时间尺度效应下对系统簇发振荡行为的影响机理.
1 数学模型
蔡氏电路作为一种简单的非线性电子电路,其制作的容易程度使它成为当前众多混沌电路中最具代表性的一种,成为许多研究的对象,并广泛被人们在文献中引用[30-31].基于广义蔡氏电路模型,本文建立了一个电路系统(图1),其中包含两个电感L1和L2,两个电容C1和C2以及一个分段线性的非线性电阻RG,同时并联一个周期变化的电流源iG,其相应的动力学模型可以表示为

图1 电路原理图Fig.1 Schematic circuit diagram
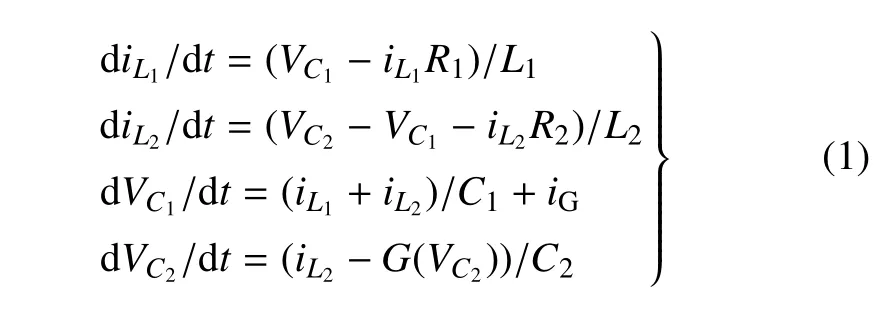
其中,非线性电阻的伏安特性为G(VC2)=P2VC2+0.5(P1−P2)(|VC2+E0|−|VC2−E0|),周期变化的电流源特性为iG=IGsin(ωt).引入变换t=R2C1τ,x=R2iL1,y=R2iL2,u=VC1,v=VC2,则式(1)可表示为如下无量纲形式

固定参数量级为α ≡O(10−4),Ω ≡O(10−2).由于系统的固有频率ΩN(可由在α=0 且A=0 时系统(2)的平衡点特征值的虚部近似估计)的量级一般为1,因此,此时系统中存在明显的3 个尺度,即T1≡O(1),T2≡O(10−2),T3≡O(10−4).如果将外激励项Asin(Ωτ)视为参数w,则系统(2)分别对应着3 个子系统,表示为

将中间尺度变量所对应的子系统(4)与快尺度变量对应的子系统(3)合并为一个非自治系统,表示为

于是将原来的三时间尺度耦合系统(2)重新划分为快子系统(6)与慢子系统(5),从而可以将三时间尺度耦合问题(3)∼(5)转化为两时间尺度耦合问题(5)与(6)来分析讨论.
2 快子系统稳定性分析
由非线性电阻RG的分段线性的特性,快子系统(6)中存在两个非光滑分界面,其中,H±(v)=v−(±1),从而其状态空间被Σ±1划分为3 个不同的光滑区域,表示为

分别对应3 个非自治的光滑子系统
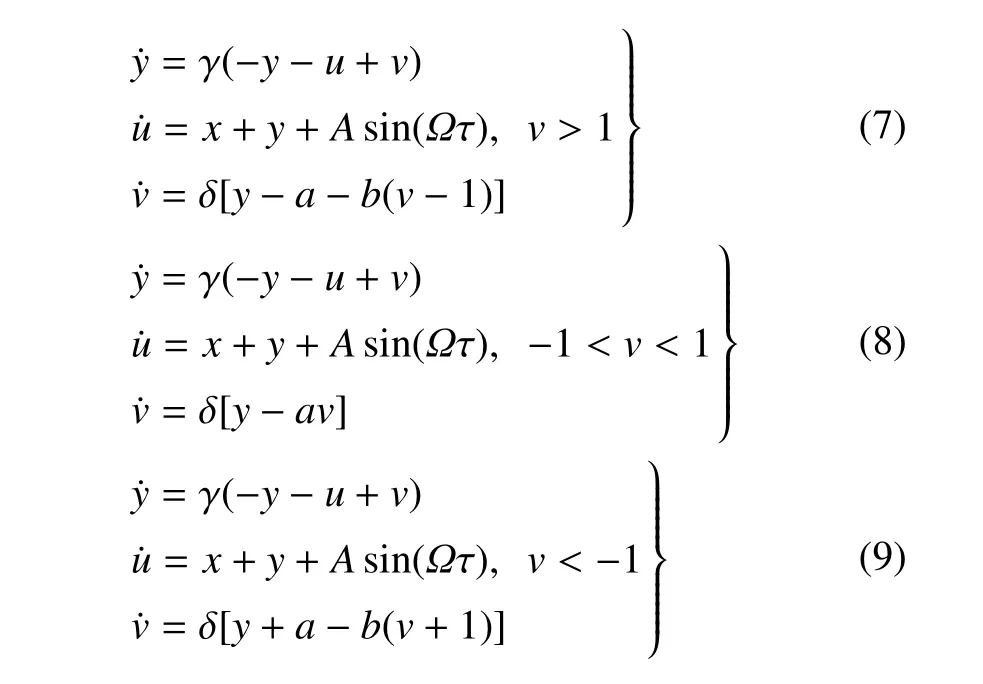
其向量场依次记为F1,F2,F3.快慢耦合系统(2)的慢子流形,即系统(6)的平衡态,这里称之为名义平衡轨道(nominal equilibrium orbits),记为NEO,其解析形式可设为

其中,Y0,U0,V0,Ai,θi(i=1,2,3)是常数,可以通过把(10)分别代入系统(7)∼(9)中得到.例如,对区域D3中的名义平衡轨道NEO−有

从名义平衡轨道的解析形式(10)可以发现,外激励的作用是对无激励情形下对应的线性自治系统的平衡点位置的扰动,因此,名义平衡轨道可以看作是由一系列周期为2π/Ω 的极限环组成的平衡态.由于名义平衡轨道在非光滑分界面所划分的子区域内满足处处等价,所以对名义平衡轨道的稳定性的讨论可以转化为对名义平衡轨道上一个点的稳定性的讨论.根据系统的对称性,D1与D3中的名义平衡轨道NEO+,NEO−具有相同的特性,统一记作NEO±,与之相应的特征方程为
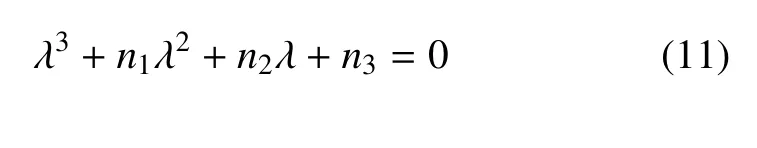
其中,n1=δb+γ,n2=γ −δγ+γδb,n3=γδb.由Routh-Hurwitz 判别准则知,当参数满足条件n1>0,n3>0,n1n2−n3>0 时,NEO±是渐近稳定的.随着参数的变化,NEO±可能存在以下两条失稳路径:
(1)FB±:=n3=0(n1>0,n2>0),此时,特征方程(11)有零单根出现,系统可能产生fold 分岔;
(2)HB±:=n1n2−n3=0(n1>0,n2>0,n3>0),此时,特征方程(11)有共轭纯虚根出现,系统可能产生Hopf 分岔.
类似可以讨论区域D2中NEO0的稳定性.
固定部分参数如下:α=0.000 1,β=1.2,a=−3.0,b=0.6,A=0.5,Ω=0.01.图2 给出了快子系统(6)在(γ,δ)参数平面上的γ >0,δ >0 且慢变量x=0 时的双参分岔情况.图中曲线HB反映了名义平衡轨道NEO±的一对复特征值通过穿越纯虚根失稳的临界情形.取γ=0.6,表1 给出了参数δ 分别取1.02,1.1456 和1.1584 时非光滑分界面两侧的快子系统的名义平衡轨道NEO±所对应的特征值.
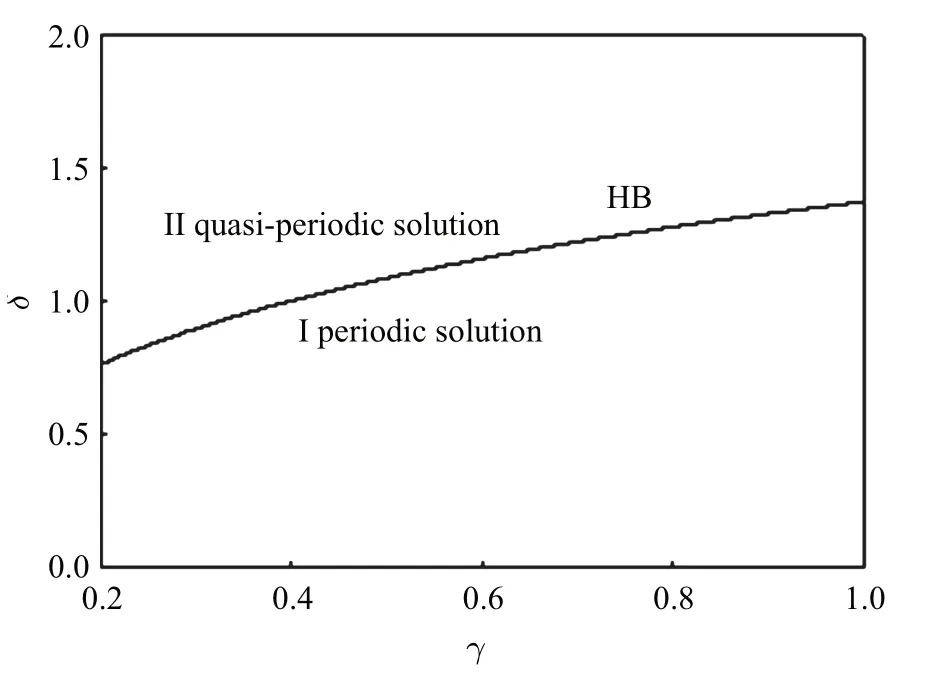
图2 快子系统(6)在(γ,δ)平面上的双参分岔图Fig.2 Two-parameter bifurcation diagram of fast subsystem(6)on(γ,δ)plane

表1 快子系统的名义平衡轨道对应的特征值Table 1 Eigenvalues of the NEOs of the fast subsystems
结合表1 知,图2 中分岔曲线HB将参数平面分为两部分:当参数在曲线HB下方的区域I 中取值时,特征方程(11)的所有的根具有负实部,意味着名义平衡轨道NEO±为稳定的,即快子系统(6)在区域D1,3中存在两个稳定的极限环;当参数从区域I 穿越曲线HB进入区域II 后,名义平衡轨道NEO±失稳,意味着快子系统(6)的原来的两个稳定极限环将转变为对应的两个概周期运动,如图3 所示.
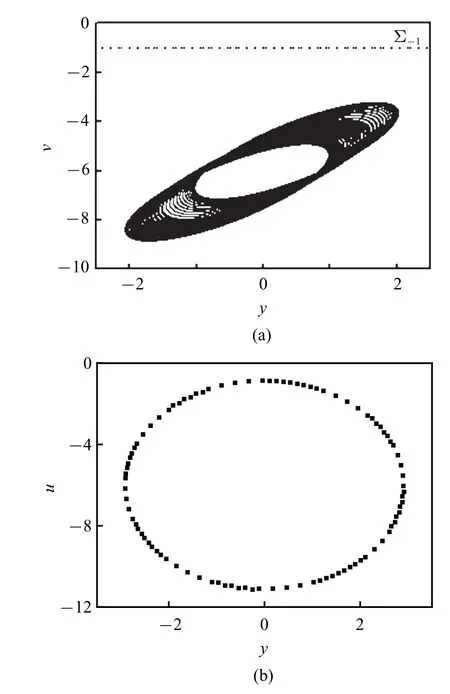
图3 (a)区域D3中的概周期解;(b)庞加莱截面图Fig.3 (a)Quasi-periodic solution in D3;(b)Poincare section
随着慢变量x的连续变化,无论是区域I 中的名义平衡轨道NEO±所对应的稳定极限环,还是区域II 中出现的概周期运动,都可能会接触到非光滑分界面Σ±并出现非光滑分岔,进而影响三时间尺度耦合系统(2)的动力学演化机制.接下来,将通过具体的数值,进一步探讨分析非光滑分岔对簇发振荡的吸引子结构以及转迁机制的影响.
3 簇发振荡的动力学演化过程及机制分析
3.1 簇发振荡
图4 和图5 分别给出了当参数δ=1.02,δ=1.158 4 时系统(2)的簇发振荡的相图及其对应的时间历程图.

图4 δ=1.02 时的周期簇发振荡Fig.4 Periodic bursting oscillation for δ=1.02

图5 δ=1.158 4 时的混沌簇发振荡Fig.5 Chaotic bursting oscillation for δ=1.158 4

图5 δ=1.158 4 时的混沌簇发振荡(续)Fig.5 Chaotic bursting oscillation for δ=1.158 4(continued)
当参数δ=1.02 时,从(y,v)平面中的相图4(a)中可知,整个周期运动关于原点对称,运动方向如图中红色箭头所示.根据时间历程图4(b)可计算得其频率近似为0.000 270 9.接下来详细阐述此时的三时间尺度下周期簇发振荡的吸引子结构.
不失一般性,设系统轨线从非光滑分界面Σ+1上的点A1出发.随着时间的变化,轨线进入光滑区域D2中.之后,迅速向非光滑分界面Σ−1运动并且在点A2穿过Σ−1而进入光滑区域D3中.此后,轨线在区域D3中首先呈现明显的密集的螺旋形振荡行为.根据时间历程图可以发现,轨线的振幅是逐渐减小的.经计算,轨线的振荡频率近似为0.562 5.随着时间继续延长,轨线逐渐由密集的振荡形式转为舒缓的振荡形式,且振幅基本保持不变,对应的近似振荡频率为0.01,直到轨线抵达非光滑分界面Σ−1上的点A3.之后,轨线在的运动过程中,将重复轨线在中的相似运动过程,并最终返回出发点A1,完成一个周期的运动.从上述结果发现,周期簇发振荡的近似频率0.000 270 9 与最慢的时间尺度T3≡O(10−4)基本吻合;从非光滑分界面跳入区域D1,3并逐渐收敛时的近似振荡频率0.562 5 与最快时间尺度T1≡O(1)基本一致;轨线的振幅稳定后的近似振荡频率0.01 与外激励频率所对应的时间尺度T2≡O(10−2),即与中间时间尺度相吻合.可见,此时的簇发振荡明显地具有3 个不同量级的振荡频率,体现了系统的三时间尺度效应.
而当参数δ=1.158 4 时,快子系统的名义平衡轨道NEO±由于所对应的特征值穿越纯虚根而失稳.此时,系统(2)表现为明显的混沌行为(见图5),且其轨线在来回穿越非光滑分界面的过程中,连接了光滑区域D1与D3中的概周期运动,可以称作概周期−概周期型混沌簇发振荡.
3.2 簇发振荡的机制分析
主要探究δ=1.02 时的演化机制.考虑到系统的对称性,仅探究过程.
利用转换相图 (TPP)与慢子流形的叠加图(图6(a)),在(x,v)平面内利用快慢分析法,结合非光滑分界面处的分岔分析,进一步来探讨图4 中具有的三时间尺度特性的周期簇发振荡的振荡机理,也即系统在呈现三时间尺度的簇发振荡时,轨线在不同时间尺度之间的转迁机制.
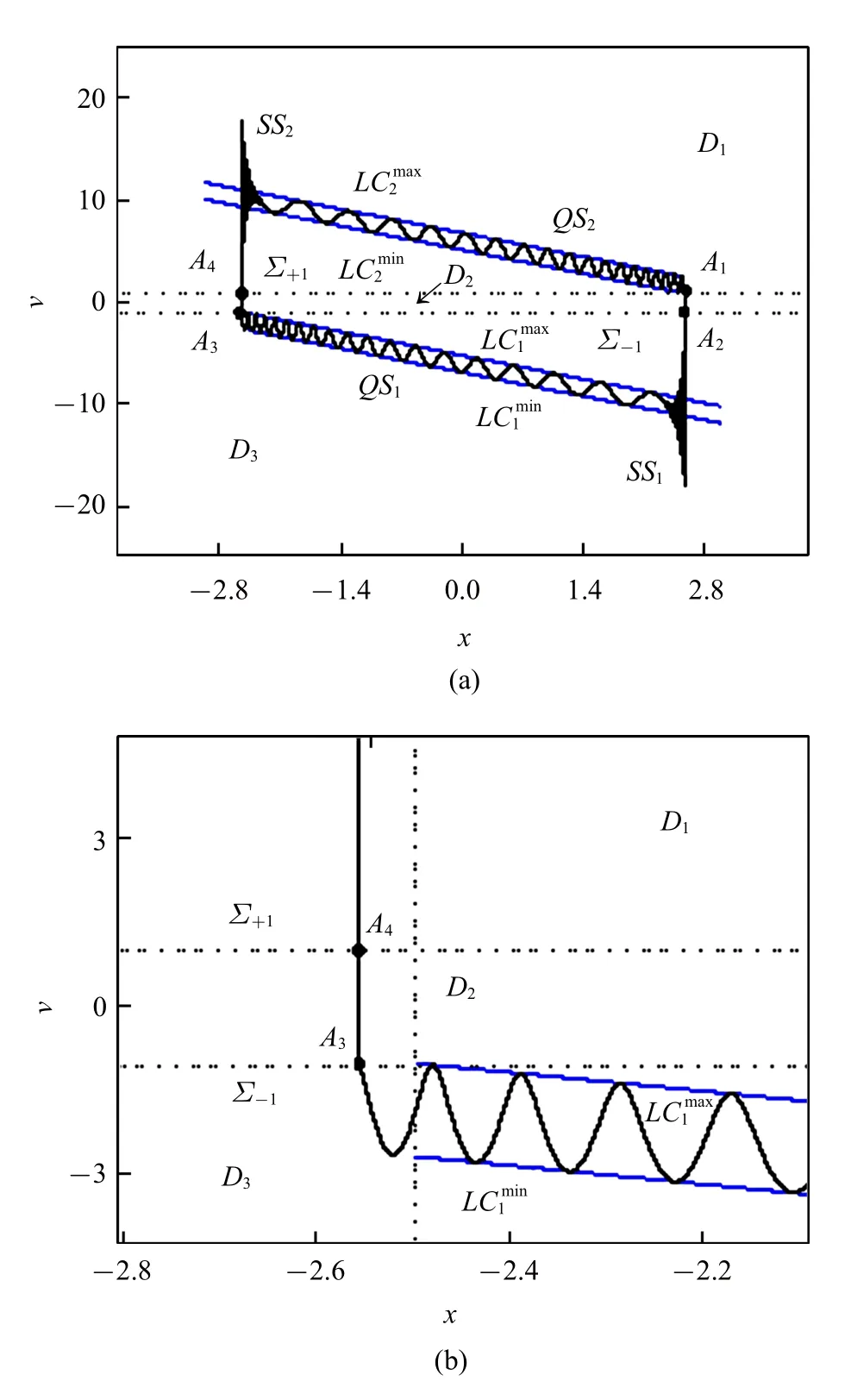
图6 (a)δ=1.02 时转换相图与慢子流形的叠加图;(b)局部放大图Fig.6 (a)Overlay of TPP and the manifold of the fast subsystem for δ=1.02;(b)enlarged figure
事实上,在中间尺度系统(4)的激励作用下,快子系统的具有解析形式(10)的名义平衡轨道NEO−表现为区域D3中的稳定极限环LC1.随着慢变量x在时间尺度T3≡O(10−4)上的连续变化,LC1将在空间中形成环面结构形式的慢子流形.快子系统(6)的极限环LCi(i=1,2)在v轴方向的极值分别记为,如图6 中的蓝色线条所示.
如上,轨线仍从Σ+1上的点A1出发,由于光滑区域D2中名义平衡轨道的不稳定性,轨线迅速向非光滑分界面∑−1运动并在点A2穿过Σ−1而进入光滑区域D3,在收敛到具有不变环面结构的稳定慢子流形的过程中出现大幅振荡,形成激发态,记作SS1,其振荡频率与慢子流形对应的平衡点的虚部基本吻合,体现了系统的最快时间尺度T1≡O(1).随着时间的增大,轨线的振幅逐渐减小.当系统轨线收敛到稳定慢子流形上后,将沿着慢子流形呈现振幅保持不变的环面运动(对应的两条蓝色曲线之间的距离保持不变),形成沉寂态,记作QS1,其振荡频率与外激励保持一致,体现了中间时间尺度T2≡O(10−2).由于轨线在从激发态SS1转迁到慢子流形上的沉寂态QS1的转迁过程中并没有分岔出现,所以只是轨线收敛的暂态过程的体现.
然而,从D3中的沉寂态QS1向D1中的激发态SS2的转迁是系统轨线通过依次穿越非光滑分界面上的点A3与A4的形式完成的.但是,通过快子系统(6)的稳定极限环LC1可以发现(见图6(b)),LC1在慢变量跨过x=−2.5(对应图6(b)中的垂直方向的虚线)后消失了.即随着慢变量的减小,虽然慢子流形的稳定极限环LC1消失了,但是轨线并没有立刻向激发态转迁,而是继续保持了一段时间的沉寂态,直到轨线穿越非光滑分界上的点A3后才向激发态转迁.因此,慢子流形所对应的非光滑分岔将对此处的转迁机理起到至关重要的作用.
下面对快子系统在非光滑分界面上的非光滑动力学演化进行分析.
由于非光滑分界面Σ−1两侧的向量场的连续性,在非光滑分界面Σ−1上存在一条分割曲线,满足

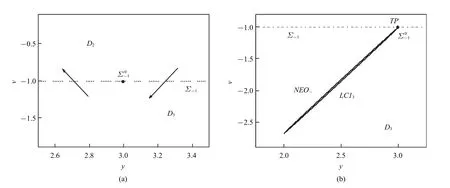
图7 (a)非光滑分界面Σ−1上的动力学分析;(b)x=−2.5 时与Σ−1相切的NEO−;(c) x=−3 时与Σ−1横截相交的NEO−;(d)x=−2.6 时的时间历程图Fig.7 (a)Dynamic analysis on non-smooth interface Σ−1;(b)NEO−tangent to Σ−1for x=−2.5;(c)NEO−intersecting with Σ−1for x=−3;(d)time history for x=−2.6

图7 (a)非光滑分界面Σ−1上的动力学分析;(b)x=−2.5 时与Σ−1相切的NEO−;(c) x=−3 时与Σ−1横截相交的NEO−;(d)x=−2.6 时的时间历程图(续)Fig.7 (a)Dynamic analysis on non-smooth interface Σ−1;(b)NEO−tangent to Σ−1for x=−2.5;(c)NEO−intersecting with Σ−1for x=−3;(d)time history for x=−2.6(continued)
另外,由名义平衡轨道NEO−的解析表达式可知,∂V0/∂x=−5/3 <0,即随着慢变量x的减小,NEO−将向非光滑分界面Σ−1移动.经计算,慢变量x=−2.5 时,NEO−与非光滑分界面Σ−1相切于直线上的点TP,如图7(b)所示,意味着对应的极限环LC1此时也与分界面Σ−1相切于点TP,且保持存在.随着慢变量x的减小,名义平衡轨道NEO−将跨越分界面Σ−1,图7(c)给出了对应x=−3 时的名义平衡轨道NEO−.此时,NEO−被非光滑分界面Σ−1分割为两部分:一部分位于光滑区域D3内,为真实存在的部分,对应图7(c)中的黑色实线部分,记为NEOR−;另一部分位于光滑区域D2内,不满足非光滑限制条件,对应图7(c)中的红色实线部分,记为.而此时,与名义平衡轨道NEO−相应的存在于快子系统(6)的极限环LC1却在光滑区域D3内到达非光滑分界面Σ−1后进入了图7(a)中的左侧区域,受到该分界面的非光滑动力学特性的影响,轨线将直接按照图中箭头所示的方向横截穿过Σ−1与Σ+1向光滑区域D1内的稳定极限环LC2转迁,如图7(d)所示,意味着极限环LC1消失.
鉴于极限环LC1随着慢变量x的变化所展现的由光滑区域D3内的稳定极限环,经过与非光滑分界面Σ−1相切的临界情形,再到与Σ−1横截相交后消失的动力学演化过程,这里称其为环的破坏性擦边分岔,记为CGB.
回到系统(2)的轨线在非光滑分界面Σ−1上的点A3处由沉寂态QS1到激发态SS2的转迁机制.如图6(b),当慢变量越过x=−2.5 时,虽然极限环LC1(NEO−)由于破坏性的擦边分岔而消失,但是在区间x∈(−2.5,−3.5)上,名义平衡轨道NEO−在光滑区域D3中仍然存在着部分,也即慢子流形在区间x∈(−2.5,−3.5)上仍然存在,并且仍然落在直线的左边(图7(c)).因此,沉寂态QS1在慢变量x越过x=−2.5 后会继续存在,直到轨线到达非光滑分界面Σ−1上的点A3.此时,受到极限环LC1(NEO−)的破坏性的擦边分岔CGB 的影响,轨线直接穿过非光滑分界面Σ−1而进入光滑区域D2,意味着沉寂态QS1的结束.
这样,在A1A2A3过程中,系统呈现三时间尺度的簇发振荡时,轨线在不同时间尺度之间的转迁机制得到了完整的解释.根据文献[11]中提供的对簇发振荡的命名和分类的方法,也即以导致沉寂态与激发态之间转迁的分岔对簇发振荡进行命名和分类,同时考虑到此时对应的周期簇发振荡中体现出的三时间尺度效应,图4 中的周期簇发振荡可称为对称式CGB/CGB型三时间尺度周期簇发振荡.
当δ=1.158 4 时,由于对应的快子系统的概周期运动同样会在跨越慢变量的临界值后失稳,在非光滑分界面Σ±1上经历破坏性的擦边分岔,导致概周期运动破裂,表现了典型的由概周期运动破裂到混沌行为的动力学演化过程,形成了此处的概周期−概周期型混沌簇发振荡.
4 结论
基于典型的蔡氏电路,文章建立了一个含有三时间尺度的四维分段线性系统.以此系统为例,将中间尺度变量视为对快尺度变量的扰动,并由此将中间尺度变量与快尺度变量看作一个整体,从而将三时间尺度耦合问题转化为两时间尺度耦合问题去分析.在此方法的基础上,利用快慢分析法,讨论了系统在两组不同数值情形下的簇发振荡行为并给出了相应的分岔机制.发现,当名义平衡轨道为稳定的时候,系统轨线能够落于慢子流形上并能够随着慢子流形穿越非光滑分界面,呈现周期簇发振荡的同时体现出三时间尺度的特性;而当名义平衡轨道通过穿越纯虚根的路径失稳后,轨线不能够落于慢子流形,而是表现为混沌运动.经过分析,非光滑分界面处的非常规分岔,即破坏性的擦边分岔是导致簇发振荡的主要诱因,为全新的通向簇发振荡的演化路径.需要指出的是,对于时间尺度具有量级差的多时间尺度耦合动力系统而言,不同时间尺度之间差异到何种程度才能够出现簇发现象,这一点需要在后续工作中重点关注.另外,慢时间尺度在一定范围内变化时,是否会导致不同的簇发振荡的出现或者其它的复杂动力学现象的产生,这一点也需要在后续工作中关注.
