近地小行星极短弧定轨的进化算法研究1)

李鑫冉 赵海斌

∗(中国科学院行星科学重点实验室,紫金山天文台南京 210034)

†(月球与行星科学国家重点实验室,澳门科技大学澳门 999078)

∗∗(中国科学院比较行星学卓越创新中心合肥 230026)

引言

近地小行星是太阳系内一类特殊的天体,部分近地小行星轨道可能与地球相交,对地球安全和人类生存环境构成潜在威胁,如6500 万年的全球物种大灭绝[1]、2013 年俄罗斯的车里雅宾斯克陨石坠落事件[2-3]、发现于2004 年6 月著名的危险小行星(99942)Apophis[4].因此,发现、监测近地小行星并计算其与地球的碰撞概率、开展危险程度的评估等相关研究是十分重要的,而其中能利用较少数据尽早确定近地小行星的轨道参数尤为关键,小行星参数的精确度对碰撞模型和危害评估的结果有很大影响[5],准确的轨道参数可以为后续的预警工作提供可靠的输入,而这就涉及到小行星的定轨问题.

NASA 在 2005 年提出对至少 90%的直径超过 140 m 的近地天体进行编目和特性获取[6],Pan-STARRS[7]、Catalina[8]、NEOWISE[9]及LSST[10]、NEOCam[11]等大量的近地小行星大视场巡天项目的开展使得巡天能力不断增强,得到了大量的观测数据.但同时,新的观测方式也使得无法对巡天中探测到的每一个目标进行后续的跟踪观测,因此获得的弧长都很短,通常只有一个晚上的拍摄[12].为了提高巡天效率,未来采集的数据将会更为稀疏,并且轨道参数分布范围很广,包含众多大偏心率轨道,这些短而稀疏的数据给轨道确定以及识别带来了很大困难.对于这些过短的观测弧段尤其是大偏心率极短弧段,利用传统的Laplace 和Gauss 方法无法进行定轨,加之短弧定轨本身具有的病态性[12-16],使得定轨难度大幅度增加.由此,如何有效利用这些数据对小行星进行极短弧定轨,对巡天项目的充分利用及小行星的探测研究都有着重要意义.近年来针对这类问题,极短弧定轨的概念被明确提出并成为研究热点.极短弧的具体弧长目前尚无严格的定义,通常无法用经典方法得到合理定轨结果的观测弧段即称为极短弧,以区别于传统意义上的短弧定轨[12-13,17-18].

除经典计算方法外,优选法也可被利用来解决定轨问题,优选法克服了经典方法中迭代不收敛的现象,但更适合于解决一维的优选问题.对于多维情况,计算过程过于复杂.此外,方法对于初值的要求较高,而初值选取本身就是一个初轨计算问题,对于极短弧轨道计算问题也不适用.

Ansalone 和Curti[18]针对极短弧定轨问题下天基的模拟资料,应用遗传算法(genetic algorithm,GA),将观测首末时刻的斜距作为优选变量,使定轨问题转换为一个优化问题,但采用的参数与通常选法相差较多.王志胜等[19]传算法运用到短弧定轨的问题上来,研究基于测角资料的卫星短弧定轨.刘磊等[20]将遗传算法应用于天基的短弧定轨问题,采用双ρ 迭代模型,对稀疏数据进行定轨.李鑫冉和王歆[21-22]对参数调整后将遗传算法应用到了极短弧定轨问题中,在地基的空间目标定轨问题中得到了较好的应用.进化算法在优选问题中可以将生物进化中优胜劣汰的现象应用到对最优解的搜寻中,在探索过程中通过积累经验,启发式地寻找最终解.算法已有较为成熟的理论基础,在多个领域都有研究和应用[23-24].算法对先验信息的依赖性较小,受数据中的噪声影响也较小,采用进化算法研究定轨问题已成为新的趋势.除遗传算法外,进化算法中还包含多种不同进化机制的算法,算法各有特点和优势,粒子群算法(particle swarm optimization,PSO)、差分进化算法(differential evolution,DE),及基于统计学思想的分布估计法(estimation of distribution algorithm,EDA)等已被应用于解决空间目标的短弧定轨问题,并在近圆轨道下有较好表现.

本文将进化算法引入小行星的极短弧定轨问题,构建计算框架,以差分进化算法为代表采用模拟资料进行计算验证,并比较算法在不同偏心率下短弧定轨问题中的表现,探讨大偏心率下算法的特征.

1 进化算法

20 世纪60 年代进化算法基于模拟自然进化的方法首次被提出,70 年代出现了相关的理论研究,直至21 世纪基本成熟[25].

这其中最具代表性的就是GA 算法,算法通过模拟自然进化中优胜劣汰的过程搜索最优解,基于适应度来选择父代进行杂交,GA 算法产生的子代有概率发生变异,从而在进化的同时寻找新的可能性.从20世纪70 年代被Holland 和De Jong 提出以来被广泛应用,收敛性和全局搜索能力已得到证明[25].

PSO 算法于1995 年被Kennedy 和Eberhart[26]提出,源于对鸟类捕食行为的研究,即鸟类找到食物最简单有效的方法就是搜寻当前距离食物最近的鸟的附近区域.与GA 算法不同,它基于群体智能而不是遗传操作,利用群体中个体对信息的分享,使整个群体的运动在问题求解空间中产生从无序到有序的演化,最终获得最优解.

DE 方法在1996 年由Storn 和Price[27]提出,是目前最有效的随机参数优选算法之一,它模拟生物进化,将初始种群中两个个体的向量差作为变异方向,叠加到第三个个体上,以此产生新个体,反复迭代使得适应环境的个体被保留下来.不同于遗传算法原本采用二进制编码适用于离散问题的求解,它适用于求解连续变量的优化问题.算法构造思想借鉴了GA 算法和PSO 算法,算法保留了GA 算法的进化过程,同时以类似于PSO 算法中的更新方法替代GA 算法中的遗传操作,因此参数和算子较少,计算复杂性降低.

进化算法的进化机制多种多样,但通常的流程是相同的.一般将需要被优选的变量称为个体,通过优选方法随机生成一定数量的个体组成初始种群.种群内个体数目称为种群数,种群数越大搜索能力也越强,但计算效率随之降低.适值函数用于评估个体优劣,即优选法中的目标函数,对于最小化问题,个体适值越小则越优秀.通过进化在满足预定条件时终止即得到最优解.具体流程如图1.

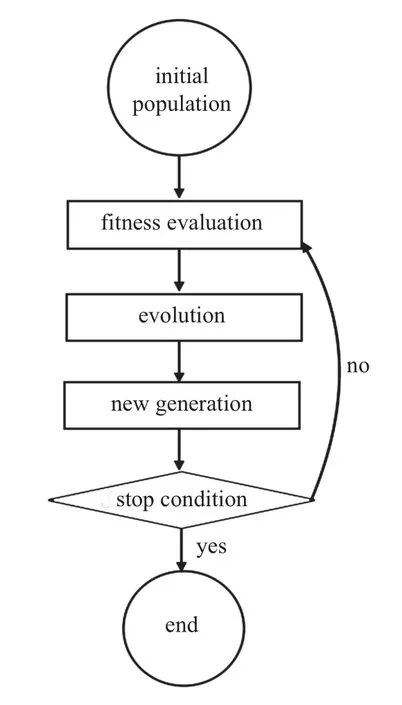
图1 进化算法流程图Fig.1 The flowchart of Evolutionary Algorithm

2 初轨计算的差分进化算法

DE 算法的主要步骤与GA 算法类似,主要包括变异(mutation)、交叉(crossover)、选择(selection)三种操作,但次序不同.算法随机生成初始种群X={x1,x2,...,xNP},其中NP为种群数,xi={xi1,xi2,...,xiD}为D维向量,D为优选变量的维数.DE 算法先进行变异操作,对每个个体xi变异得到个体Vi,变异方式较GA 算法大为简化,常见的变异方式有以下三种

(1)DE/rand/1

(2)DE/best/1

(3)DE/target-to-best/1

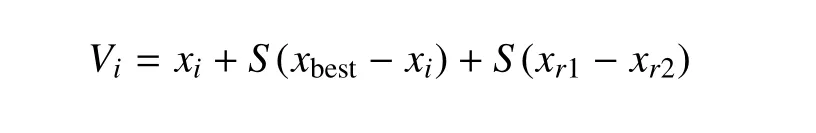
其中r为互不相同的均匀分布的随机整数,ri∈[1,NP]且ri≠i;S为缩放因子,一般在区间[0,1]中取值,但多数文献建议取较大的值,综合文献[27-30],范围在[0.4,1]比较合适,S取值决定了算法的全局搜索能力,越大的取值全局搜索能力越强;xbest为由适值函数所确定的当代最优的个体,DE/*/*是DE 算法变异的表达方式,两个* 依次表示变异基和差分数量.经变异所得的种群V={V1,V2,...,VNP}和原种群X交叉操作,得到新种群U.具体如下

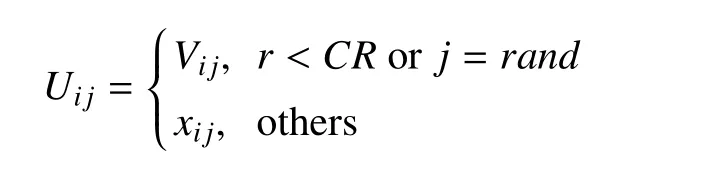
其中r为[0,1]区间均匀分布的随机数,rand为[1,D]上均匀分布的随机整数,CR为交叉概率.此操作使得Ui以一定概率接受变异个体的分量,但确保至少有一个分量来自变异个体,CR决定了种群的多样性,文献中建议CR取0.1 或0.9[27-30]作为初始尝试值.最后进行选择操作,DE 算法采用了贪婪操作,如果新个体优于初始个体,则取而代之,否则初始个体保留下来,进入下一次的进化

这里k表示进化代数,表示xi(k)进化到第k代的个体,函数F(·)表示求解个体的适值.从选择方式可看出最优个体一定会进入下一代,每一代种群不会劣于前一代.

通过上述三个操作完成了一次种群的进化,并通过不断迭代求解出最优解.算法常用操作中的选择和交叉操作都只有一种方式,而变异操作选择也比较少,且基本形式是相同的.

3 (a,e,M)优选法

3.1 变量选择

对于优化问题,优化变量过高会带来求解困难的问题,即使如今计算能力已有了大幅度的提升.因此本文采用了3 个Kepler 根数,即历元时刻t0的(a,e,M0)作为优化变量,与Ansalone 和Curti[18]采用首尾观测时刻的斜距作为优化变量的方法不同,在只增加一维的情况下,使得优化结果不再需要依赖观测量就可以得到完整的解,便于资料处理.

3.2 初始种群生成生成和终止条件

根据先验信息定义优选变量的值域,由于进化算法对初值要求较低,无确切信息时可将范围取的大一些:a∈[al,au],e∈[el,eu],M0∈[Ml,Mu].初始种群中每个个体的每个变量都在取值范围内随机选取,重复NP次即得到整个种群{xNP}.终止条件选取较为普通的迭代次数达最大进化代数G终止或连续C代没有进化.

3.3 适值函数

令已知一组观测量{ti,αi,δi,i=1,2,...,n},(αi,δi)代表ti时刻的赤经和赤纬,则由历元时刻t0的(a,e,M0)可得ti时刻黄道坐标下的近点角Mi,fi和Ei,进一步可得

其中Li=(cos δicos αi,cos δisin αi,sin δi)T,ri为ti时刻目标的日心位置矢量,ri=|ri|,ρi为目标斜距,Ri为测站的日心位置矢量可由测站地心位置矢量Re和地日位置矢量RS得到.由于地球与小行星的为相对位置分地内和地外两种情况,因此依据R和L的夹角对观测几何进行分类讨论.

当R·L<0 时,即图2 所示,此时观测目标的所在位置有A,B,C 三种情况:

(2)当|r| >|R|时,即小行星的轨道高于地球,处于位置C;

(3)其他,此时目标位置有两种可能A 或B,无法根据已有条件确定其具体位置,需分别计算.但这一计算非常容易,不会造成过多负担.

当R·L>0 时,即图3 所示,有2 种情况.

(1)|r| <|R| 时,目标轨道低于地球,但考虑到R和L的夹角,此情况不可能发生;

(2)其他,此时目标只可能位于A,即轨道在地球之上.

图2 R·L<0 时地球与小行星的位置Fig.2 The locations of Earth and asteroid when R·L<0

基于上述分析,则可得式(1).当目标位于图2 位置B、C,及图3 位置A 时,式中取“+”,其他情况取“-”,则任意一对观测时刻(tk,tj)且tk>tj,可得对应的(rk,rj)、(fk,fj),此时有适值函数

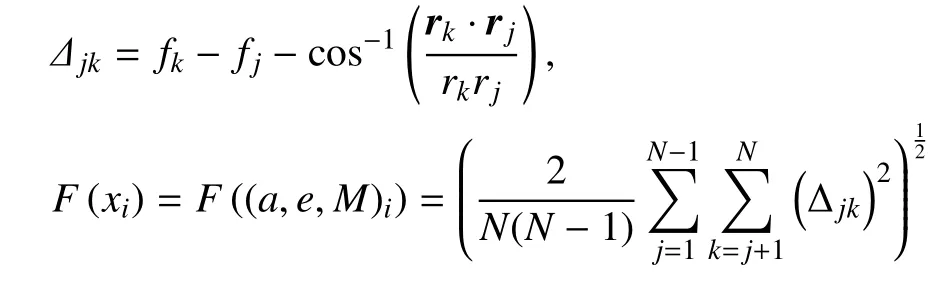
可以看出,适值越小表示个体越优.

图3 R·L>0 时地球与小行星的位置Fig.3 Locations of Earth and asteroid when R·L>0

3.4 (i,Ω,ω)的求解

通过以上计算已可得t0的(a,e,M0),从而得到每个观测时刻的位置矢量ri,从而可得(i,Ω,ω),考虑到计算精度,可由每对(ri,rj)得到的(i,Ω,ω)取多组结果的中值作为最后结果.

4 数值试验

基于DE 算法采用MATLAB 编写程序,算法参数选择NP=300,S=1.0,CR=0.9,变异方法选择DE/rand/1,最大迭代次数G=200,连续迭代次数C=30 最优适值的相对变化小于10−12则提前结束计算.考虑到近地小行星,令值域选择范围为a∈[0.8,4.0],M∈[0,2π].

选取三组偏心率不同的轨道,分别计算其轨道根数,并与传统的Laplace 方法进行比较.表1 给出了实测数据与模拟数据的定轨结果,模拟数据基于其观测数据的初始时刻、观测时刻和测站数据生成,同时保留了观测的几何构型,其中POD 代表已获得的轨道根数,作为参考标准.

表1 小行星实测数据与模拟数据定轨结果Table 1 The results of orbit determination with measured data and simulated data

可以看出,模拟数据下两种方法都可得到初轨结果,Laplace 方法更接近准确值.采用实测数据时,当偏心率较小,DE 算法的结果偏差稍大,当偏心率逐渐增大时,Laplace 方法的结果偏离程度增大,至e>0.6时,已得不到有效结果,而DE 算法虽然出现偏差,依然可以得到有效解为后续工作提供轨道范围的参考信息.另一方面,Laplace 方法只能由单一解判断轨道信息,当计算出现困难时,得到的结果完全无效,无法指导后续工作.而进化算法的结果并不仅仅是单一的解,有效范围内的解都是有效的,可根据多组解的分布判断结果的有效性,并提示其存在范围.对于大偏心率极短弧轨道,DE 算法的适用性更广.

极短弧定轨问题本身存在困难,当偏心率增大时变得更为复杂,稀疏数据中的误差也可能对计算带来很大影响,因此,为了重点关注算法的计算规律,采用模拟数据对问题进行简化,主要探讨DE 算法在极短弧下解的特征.增加不同偏心率的小行星进行比较,选取MPC 中小行星共9 组,已经确定的轨道如表2,偏心率覆盖[0,0.7]的范围,每组数据的时间跨度为1-3 天,数据点不足10 个.

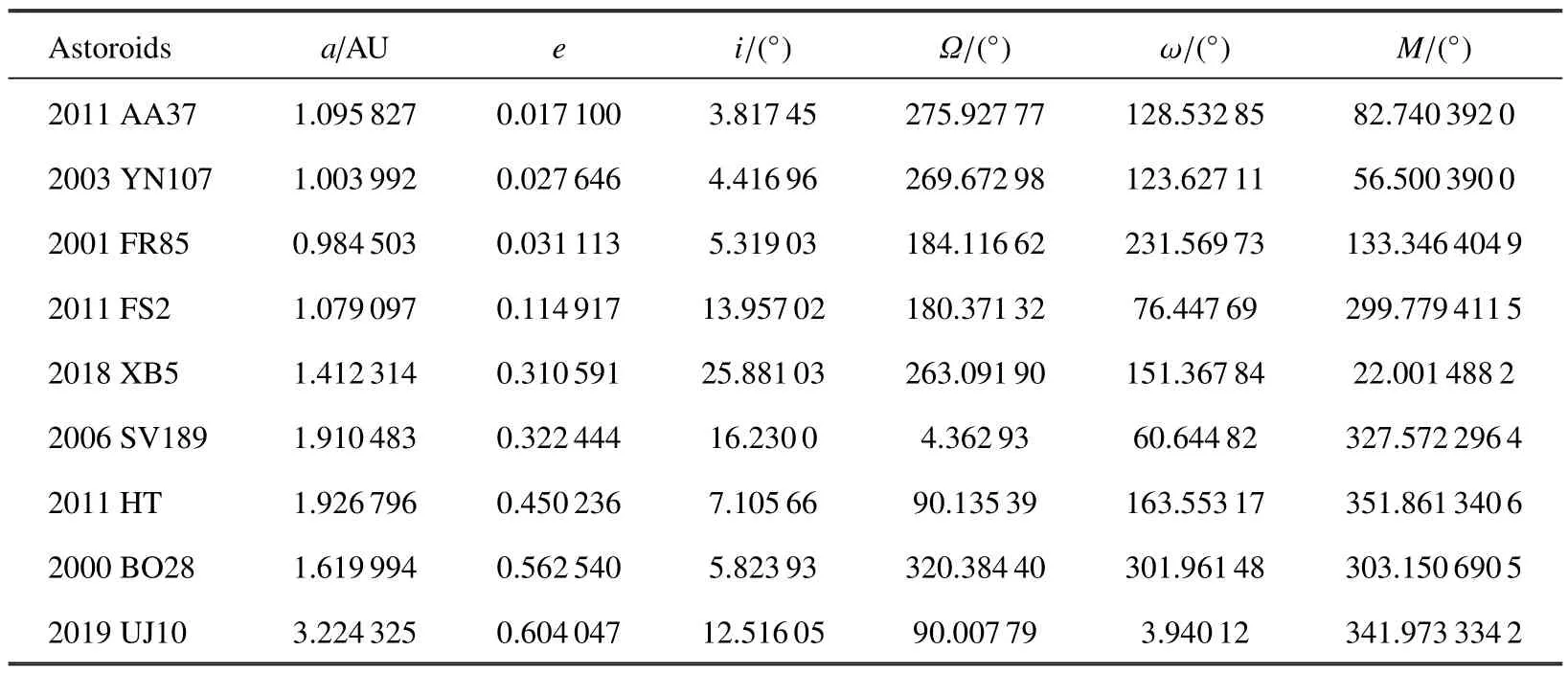
表2 小行星轨道根数Table 2 Orbital elements of asteroids

图4 给出了小行星2001 FR85 在一次完整计算过程中轨道半长径a和适值的变化.其中e∈[0.0,0.3],NP=300.可以看出DE 算法的效率很高,收敛速度很快.

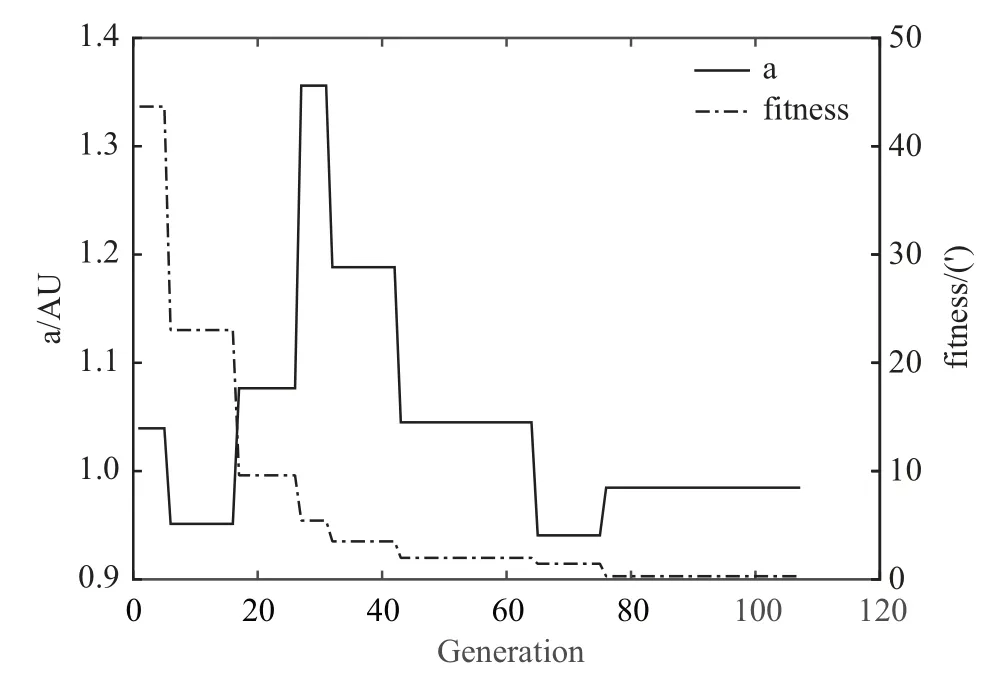
图4 半长径a 和适值F 的收敛过程Fig.4 The convergence process of the semi-major and fitness value

考虑到大偏心率定轨相较近圆轨道更为复杂,不易求解,试验时偏心率e的取值范围不直接扩大到[0,1],而是对9 组数据进行进行分类计算:当e∈[0.0,0.3]时,值域选择范围为e∈[0.0,0.3];当e∈[0.3,0.6]时,值域选择范围为e∈[0.3,0.6];当e∈[0.6,1)时,值域选择范围为e∈[0.6,0.9].为避免随机数对结果的影响,采用不同随机数对每组数据重复计算300 次.计算发现,与在空间碎片的计算结果不同,优化结果的适值差异明显,并不像近圆轨道的解那样彼此接近,因此适值的差异性同样需要关注.表3 列出了2001 FR85,2006 SV189,2019 UJ10 各自适值最小的前5 组优选结果.算法虽然不同于空间碎片近圆轨道下可以迅速准确找到轨道信息的表现,但从适值大小分析,真实解在适值上仍具有较为明显的优势,且小偏心率的适值优势比大偏心率更加突出.仅依靠1-3 天的观测数据,得到的最优解与MPC 中给的轨道根数基本一致.

图5 给出了9 条轨道的(a,e)概率密度分布图,图中颜色越浅表示聚集度越高.可以看到,当偏心率较小(e<0.1)时,最优解主要集中分布在真实轨道附近,且与适值最小的结果相吻合,DE 算法可以得到有效的结果.而当偏心率逐渐增大(e>0.3)时,求得解的分布区域发生偏离,或出现多个分布区域,且分布最集中的区域也并不是真实解的所在区域,分布不再明显集中于真实轨道附近.2018 XB5 和2011 HT 有多个分布聚集的区域,真实解包含在其中的某个区域但不是聚集度最有优势的区域.虽然DE 算法搜索到了真解,但它在获得的多个解中并没有明显优势,个体分布较少.小偏心率的轨道更为稳定从而更易被搜索得到解,而当偏心率增大时,进化过程对观测数据的敏感性可能产生变化.

表3 各组小行星轨道根数Table 3 Orbital Elements of Different Asteroid

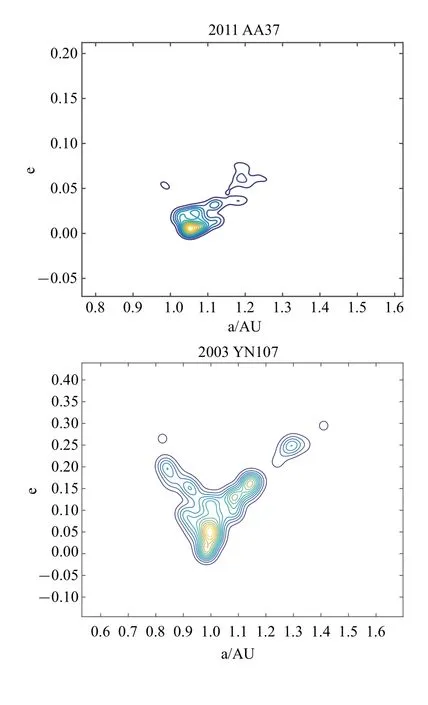
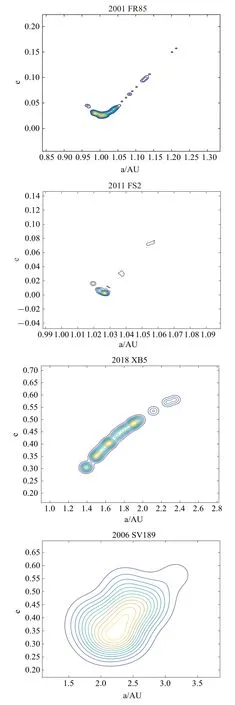
图5 概率密度分布图Fig.5 Probability Density

图5 概率密度分布图(续)Fig.5 Probability Density(continued)

因此,对于小偏心率轨道,算法易于直接寻找到最优解,而对于大偏心率轨道,需结合分布密度和解的适值进行选择,偏心率的增大使轨道更为复杂,也导致算法在搜寻最优解的灵敏度上有所下降,在搜寻过程中容易发生最优解搜寻方向的偏离,虽然可以找到适值最优的解,但数量较少,适值不具有优势的解会被大量搜索到,真实解的小范围内的聚集现象,在整体分布上没有明显优势.

2011 FS2 仅包含半天的观测数据,而2019 UJ10偏心率较大,其在概率密度分布图上的聚集更加难以显现.因此将搜索的解空间进行缩小,提高算法的灵敏度,再次进行试验.表4 中列出了2011 FS2 分别在e∈[0.0,0.3]和e∈[0.1,0.2]内搜寻的结果,均为适值最小的5 个解.可以看到随着搜索区间的缩小,搜索效率得到提高,最优解的存在被凸显出来.将2019 UJ10 的搜索空间缩小至e∈[0.6,0.7]得到了图6 的概率密度分布图.可知,虽然仍有另一个干扰解的存在,但算法明显搜索到真实解的存在区域,并且在此范围内呈现聚集状.因此算法在计算大偏心率及过短弧段的轨道时,搜索空间中真实解是存在的,只是在大范围搜索中不易搜到,聚集分布不明显.计算时可以通过将区间进行约束划分,分段计算最优解,来提高算法的灵敏度及搜索能力,提升聚集程度,同时,结果需结合解的分布聚集区域和适值最优的个体考虑.

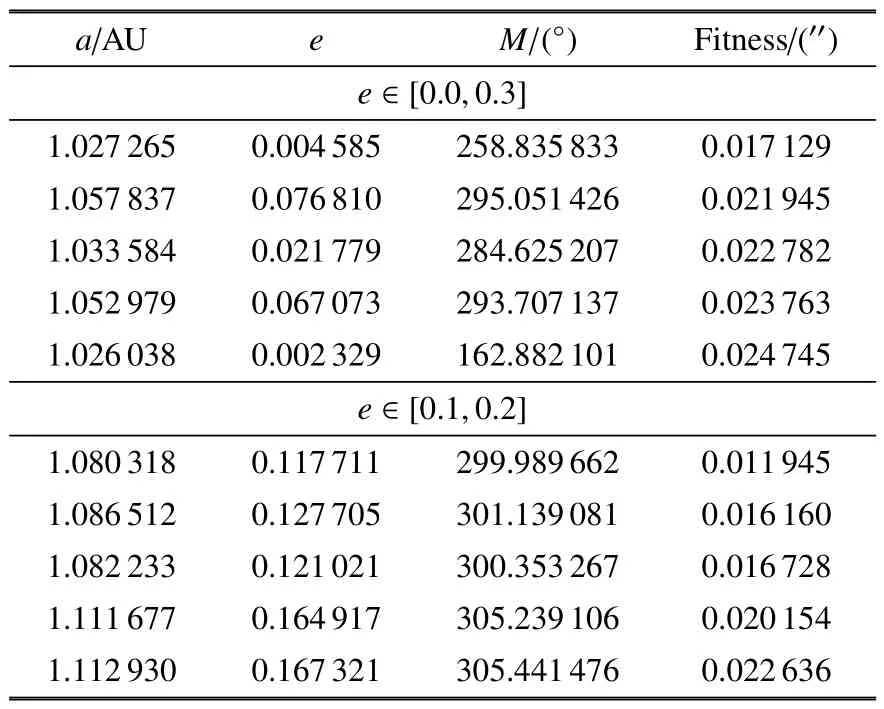
表4 小行星2011 FS2 轨道根数Table 4 Orbital Elements of 2011 FS2

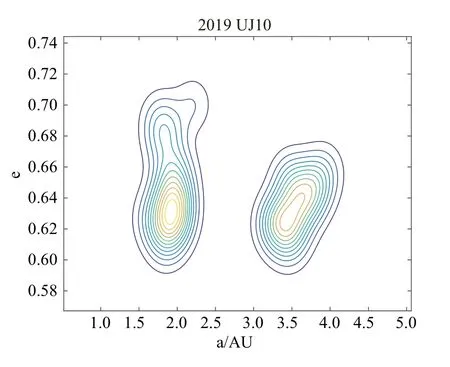
图6 e ∈[0.6,0.7]概率密度分布图Fig.6 Probability density of e ∈[0.6,0.7]

不同类型轨道受误差的影响不同,对多组模拟数据加入随机观测误差在DE 算法下进行比较.表5 给出了分别加入0.1′′,0.2′′误差的2001 FR85,2006SV189 和2019UJ10 的定轨结果.可以看到在0.1′′的误差下,仍可得到有效的定轨结果.当误差扩大到0.2′′时,解的分布仍涵盖真实解,可提示轨道信息的参考范围,但随着偏心率增大,受误差影响也增大了,大偏心率的轨道定轨结果会受到明显影响.图7 给出了约束解空间后加入0.2′′误差的2011 FS2 的概率密度分布图,星号表示真实解所在位置,在加入误差后解的分布仍覆盖真实解.

表5 加入误差的定轨结果Table 5 The results of orbit determination with error

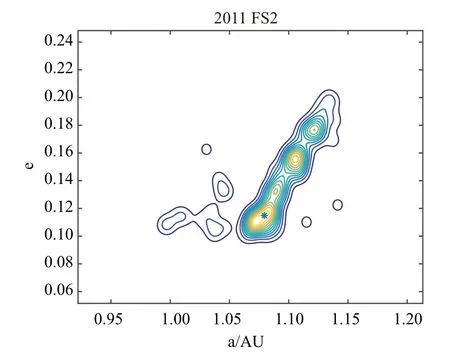
图7 加入0.2′′ 误差2011 FS2 的概率密度分布图Fig.7 Probability Density of 2011 FS2 with 0.2′′ error

5 结论

极短弧定轨问题采用经典方法存在很大困难,甚至无法得到有效解,包括DE 算法在内的进化算法将这一反问题正向处理,避免了经典方法固有的病态性,并且DE 算法参数较少,操作简便,易于实现.进化算法计算框架基本一致,只是进化机制和侧重不同,对于不同需求的问题改用不同进化算法时操作更为便捷,如EDA 方法更注重整体搜索,DE 算法更注重局部搜索,换用不同进化算法时计算框架可保持不变.

根据进化算法的特点,将其应用于近地小行星的极短弧定轨进行探索.对于小偏心率轨道,DE 算法利用少于3 天的少量数据得到的轨道信息与利用多天多站定轨下的信息一致,可为后续工作提供可参考的信息.对于复杂的大偏心率轨道和弧段更短的轨道,进化算法的表现不如小偏心率轨道下良好,搜索灵敏度降低,不易搜索到最优解,仅在局部有向最优解聚集的现象.因此,需要缩小搜索空间提高算法灵敏度,并结合分布区域和适值最优进行讨论.加入误差后,较小的误差对定轨结果影响较小,随着误差增大,尽管适值最优解受到干扰,尤其大偏心率轨道的定轨受影响较大,解的分布仍涵盖真实解所在区域.

小行星轨道较为多样,大偏心率轨道数量较多,并且实际观测中观测位置不同、与地球的相对位置不同,也会对算法产生影响,尤其对于极短弧定轨问题,数据量较少,观测数据差异和误差的影响更不可忽视.在模拟数据的研究基础上,未来需对观测位置和时刻做进一步研究,在不同情况下分类计算,提高算法在大偏心率下的搜索效率,完善进化算法在小行星极短弧定轨方面的应用.