加性和乘性三值噪声激励下周期势系统的动力学分析1)

靳艳飞 王贺强

(北京理工大学力学系,北京 100081)

引言

随机共振的概念是Benzi 等[1]在研究第四纪全球冰川期问题时提出的,揭示了噪声对非线性系统的动力学行为起到的积极有序的建设性作用的一面.近40 年来,随机共振及其相关问题的研究在理论、实验和应用方面都取得了丰硕成果[2-6].然而,这些研究成果大多集中在经典的双稳系统和阈值系统,对于复杂非线性多稳态系统中噪声诱导共振的研究较少.许多实际的工程系统、电子电路、超导器件、控制器等,其基本的模型都是基于周期势系统建立的,比如:生物马达中的棘齿模型[7]、物理领域的约瑟夫森结[8-9]、工程力学中的单摆模型[10]等.因此,周期势系统中噪声诱导的共振研究成为非线性动力学关注的热点[11-23].Fronzon 和Mannella[11]研究了倾斜的周期势系统中由噪声激励的布朗粒子的传输问题,并搭建了锁相环电路模型进行实验验证.Dan 等[13]从理论上研究了非均匀介质中质点在过阻尼周期势系统中的运动,取适当相位差时,质点的运输会随着噪声强度的变化达到随机共振的效果.Zhang[14]在恒力加白噪声驱动的欠阻尼单摆中研究了相干共振现象.Saikia 等[15-16]发现在驱动频率接近最小势阱的固有频率时,欠阻尼的周期势系统中存在随机共振现象,并把平均输入能量作为新的指标量引入到随机共振的研究中,发现两个稳定的动力学状态和随机共振的产生主要取决于系统的阻尼比和外激励的振幅.Jin 等[17-19]研究了不同噪声激励下周期势系统中的相干共振和随机共振现象,并探讨了有色噪声对系统响应和随机共振的影响.谢勇和陈若男[21]在弱周期信号极限下,利用Floquet 理论和非扰动展开法给出了一种非线性响应意义上的矩方法,对周期信号和高斯白噪声共同作用下过阻尼搓板势系统的随机共振进行了研究.Liu 和Kang[22]主要研究了非高斯列维噪声对欠阻尼周期势系统随机共振的影响,发现噪声参数对系统共振效应具有重要影响.Lou 等[23]研究了关联噪声激励下单自由度周期势系统的首次离出时间行为并讨论了系统中发生的共振激活现象.上述研究结果主要针对白噪声激励下的过阻尼系统展开,对欠阻尼周期势系统的研究较少.

噪声广泛存在于工程实际中[24-26],为了简化计算,常常将宽带或记忆时间很短的激励用高斯白噪声表示.但事实上,真正的白噪声是不存在的,故实际问题中的随机激励需要用具有非零相关时间的噪声来描述.三值噪声是一种随机电报噪声,是真实噪声的典型模型,能更好地描述自然界中的环境波动[27-29].三值噪声包含了二值噪声的情形,并且在一定极限条件下能退化为高斯白噪声或者散粒白噪声.特别地,生态系统中总存在随机环境扰动,如,环境(气温、湿度、光照等)的变化、气候变迁,这种扰动由于其多样性通常以三值或多值噪声形式表示.例如:在描述N 类种群的Lotka-Volterra 随机系统中,需要考虑随机环境对种群数量的容纳能力的影响,该随机环境激励以三值噪声来刻画[29].近年来,针对二值噪声作用下非线性系统的随机共振研究取得了一些成果[30-35].如:Jin 等[30-31]研究了二值和三值噪声激励下捕食与被捕食模型的解矩稳定性,发现相比于高斯白噪声,三值噪声更利于提高系统解的稳定性.Xu 等[32-33]利用数值方法研究了非对称二值噪声作用下双稳系统的随机共振和随机分岔,发现系统响应会呈现非对称性,且加性二值噪声的状态和强度能够诱导系统产生随机分岔现象.Fulinski[34]研究了非马尔可夫二值噪声作用下系统中噪声诱导的迁移和随机共振现象.

本文研究了加性和乘性三值噪声及外周期信号驱动下的欠阻尼周期势系统的概率密度演化和随机共振.通过数值方法得到了系统的瞬态概率密度和联合稳态概率密度函数,分析了系统参数和噪声对概率密度演化的影响.此外,利用系统平均输入能量来刻画随机共振,讨论了三值噪声强度、噪声转迁率、外周期信号振幅等对随机共振的影响.

1 系统的随机响应

1.1 动力学模型

考虑乘性和加性三值噪声及外周期力驱动下的欠阻尼周期势系统,其动力学方程如下

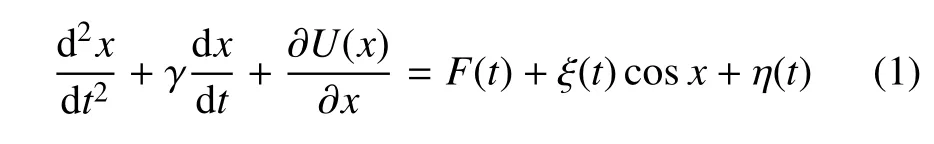
其中,γ 为阻尼系数,势函数U(x)=−sinx−bx,b是一个偏置常数,外周期力F(t)=F0cos(ω0t),这里F0和ω0分别是其振幅和频率.ξ(t)和η(t)是两个独立的三值噪声,它们的统计特性为

其中,噪声自相关时间τi,噪声强度Di(i=1,2).

对于三值噪声(2),假设ξ(t)和η(t)分别取值为{−Ai,0,Ai} (i=1,2),从±Ai到0 的转迁率为αi,其他态之间的转迁率为βi.对于对称的三值噪声,αi=βi(i=1,2).则有转迁概率满足[29]

1.2 随机响应

针对系统(1),分析系统参数对随机响应的影响.在图2 和图3 中,固定噪声强度D1=0.4,D2=0.2,b=0.2,ω0=π/4,α1=α2=10.通过数值方法对方程式(1)进行数值积分,所取的初值为x0∈[−π:π/50:π],0=0,对不同初始值得到的响应轨线进行平均,给出系统响应的时间历程图、稳态概率密度函数.从图2 来看,当阻尼系数和外周期力振幅均较小时,系统响应在x=1.5 附近振荡,即系统粒子仅在一个稳态势阱内运动,其对应的稳态概率密度是单峰结构.在图3 中,当F0增大到0.4 时,可以看到系统粒子开始在多个稳态之间跃迁,其对应的稳态概率密度是多峰结构.上述现象可以解释为,对于固定的噪声强度,通过增加外周期力的振幅能够使系统在多个势阱间做跃迁运动.

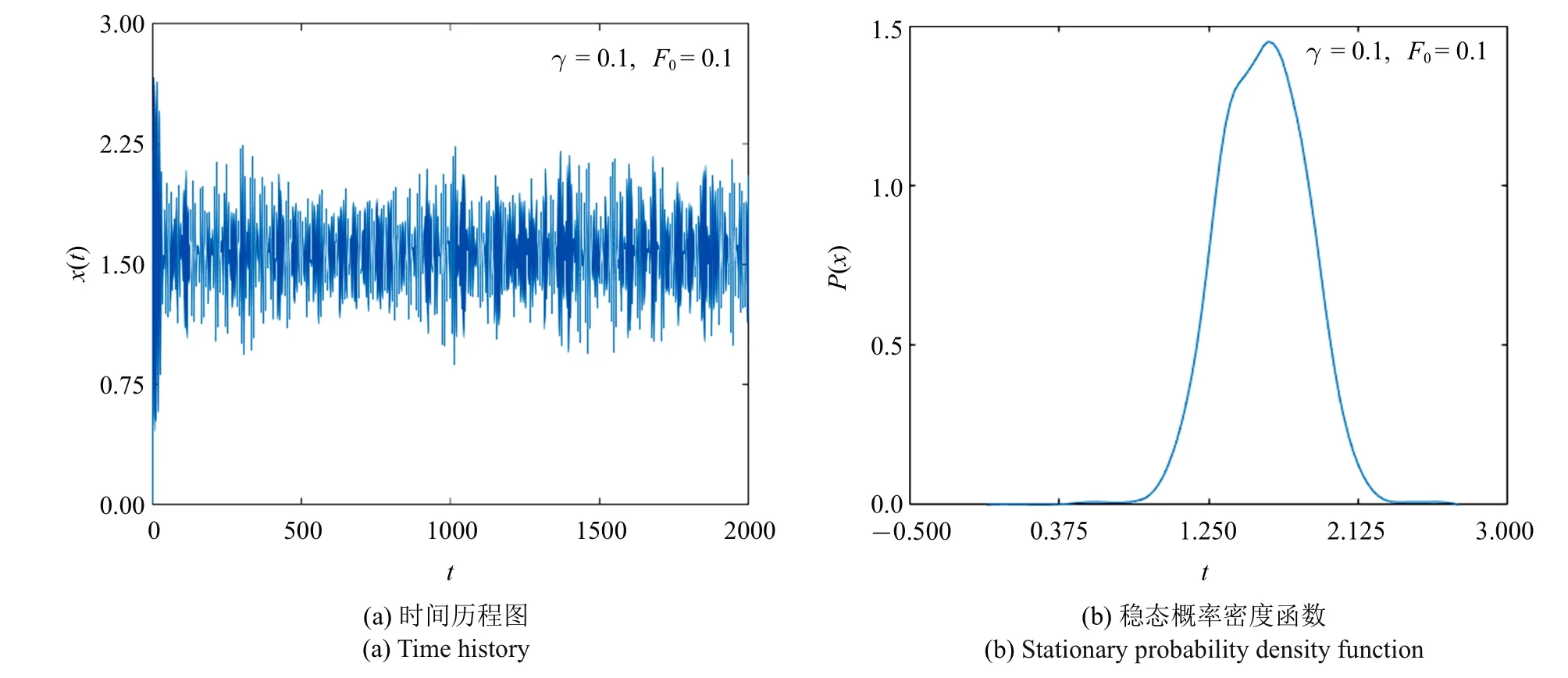
图2 系统响应的时间历程图和稳态概率密度函数Fig.2 Time history and stationary probability density function of system(1)

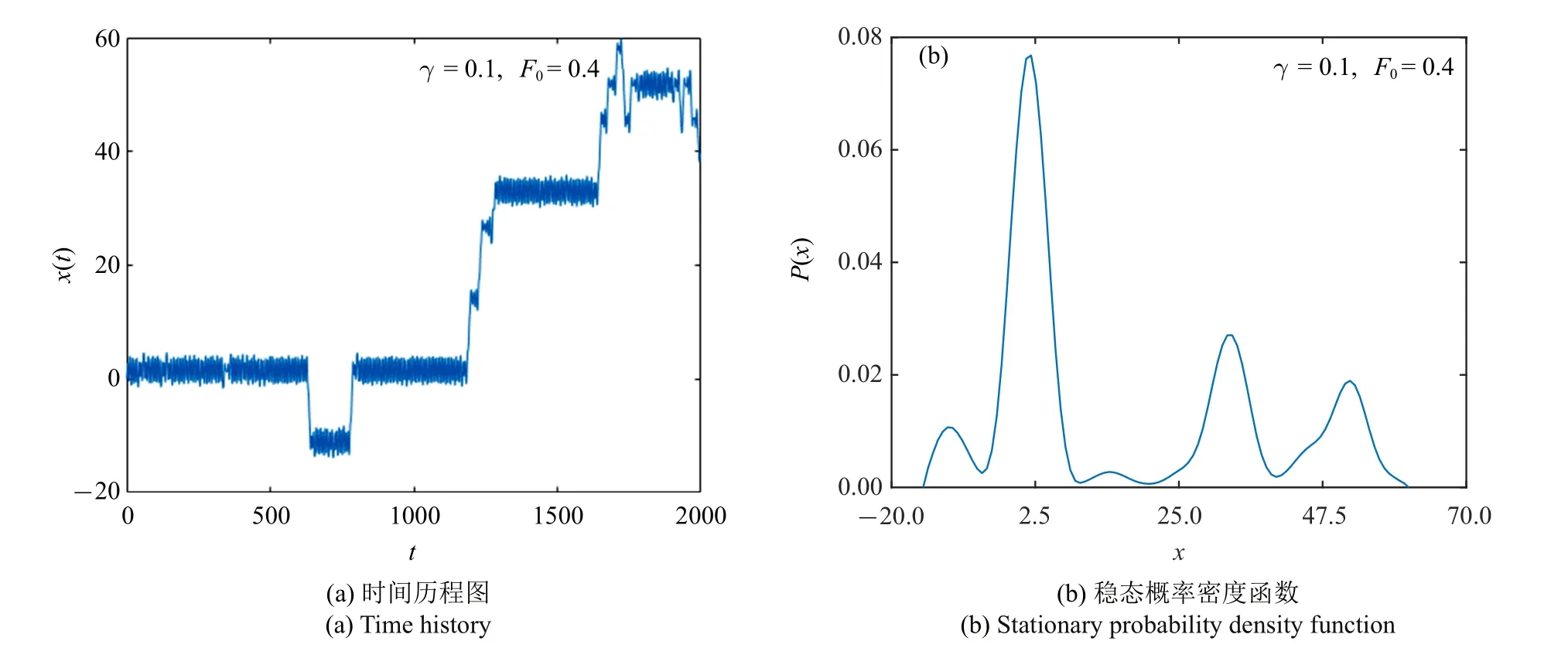
图3 系统响应的时间历程图和稳态概率密度函数Fig.3 Time history and stationary probability density function of system(1)

下面为了研究系统的联合概率密度函数的演化,对方程(1)采用蒙特卡洛方法进行数值模拟,令D1=0.2,D2=0.1,系统的其他参数选取如上.在计算区域{(x,):(−20,20)×(−20,20)}和{(x,):(−2π,2π)×(−2π,2π)} 上分别取200×200 组初始值,每个初始值计算组样例,计算系统平均稳态联合概率密度函数[36-37]和瞬态概率密度函数.图4 和图5 显示了平均稳态联合概率密度函数在外周期力作用下的演变情况.在图4 中,对于γ=0.1,一个周期内的平均稳态联合概率密度具有多个高度基本相等的峰.随着F0的增大,峰之间的跃迁更加频繁,多个峰的高度逐渐变得不相等,且随着x由−20 增大到20,峰值逐渐增大,即粒子由于F0的增加,有更大的几率运动到离稳定点更远的地方,见图4(b).图5 中固定γ=0.9,可以看出,此时的平均稳态联合概率密度函数呈现3 个独立的尖峰结构,说明随着阻尼系数的增大,势阱之间的跃迁运动变得困难,符合物理直观.对比图4 和图5,可以发现阻尼系数和外周期力振幅的变化可以引起平均稳态联合概率密度函数的形态发生拓扑结构的变化,这种现象类似于随机P-分岔现象.图6 显示了在一个周期内的不同时刻,系统瞬态联合概率密度函数在(x,y)平面内的投影,反映了联合概率密度函数的演化过程.可以清晰地看出,概率密度函数峰的位置之间相互连接,其界限比较模糊,随着时间的延长,概率密度函数峰的位置逐步演化成3个相互独立的“吸引子”,显示了瞬态概率密度函数在一个周期内的演化过程.

图4 系统的平均稳态联合概率密度函数(γ=0.1)Fig.4 Average stationary joint probability density function of system(1)(γ=0.1)

图5 系统的平均稳态联合概率密度函数(γ=0.9)Fig.5 Average stationary joint probability density function of system(1)(γ=0.9)

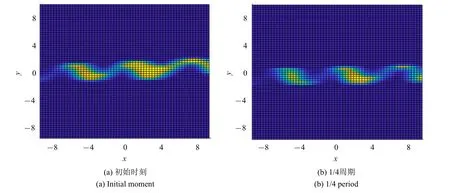
图6 一个周期内不同时刻瞬态联合概率密度函数在(x,y)平面的投影(γ=0.6,F0=1.4)Fig.6 Projection of transient joint probability density function at different moment(γ=0.6,F0=1.4)

图6 一个周期内不同时刻瞬态联合概率密度函数在(x,y)平面的投影(γ=0.6,F0=1.4)(续)Fig.6 Projection of transient joint probability density function at different moment(γ=0.6,F0=1.4)(continued)

2 随机共振

在外周期力和三值噪声共同作用下的周期势系统(1)中,布朗粒子存在有序的运动和无序的热运动,系统的随机共振体现在周期力做功随着噪声强度变化所表现出的非单调上[38],该方法也称为随机能量法.

定义外周期力在一个周期T0=2π/ω0内对系统所做的功为

将不同初始位置下的所有外加周期力输入能量式(4)进行平均,得到系统的平均输入能量

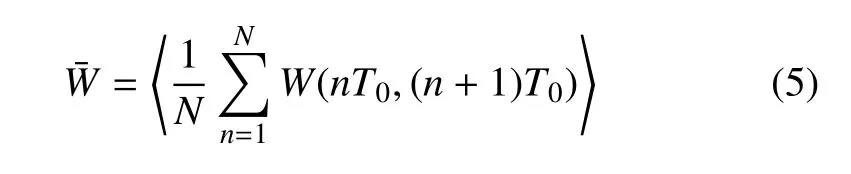
其中N是计算的周期数.

根据方程式(1)、式(4)和式(5),图7 ∼图11 分别讨论了加性噪声强度、加性噪声转迁率和乘性噪声转迁率对系统的平均输入能量的影响.在数值计算中,取γ=0.3,ω0=π/4,N=2000.图7 和图8 描述了系统分别在加性噪声激励、加性和乘性噪声共同激励下,随加性三值噪声强度D1的变化规律.在图7中,当F0分别取0.1,0.2,0.3 时,随D1的增大呈现非单调变化,有共振峰出现,即出现随机共振.随着F0的进一步增大,随D1的增大出现单调递减变化,此时随机共振消失.类似地,在图8 中固定F0=0.3,系统(1)在乘性和加性噪声共同作用下,随D1的增加出现共振峰,但是和最优的D1的值较图7 变小.总之,当噪声强度和外周期力振幅取适当值时,系统(1)会出现随机共振现象.

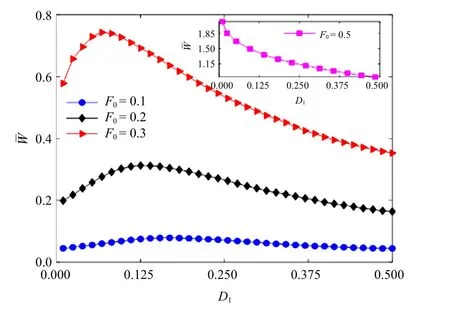
图7 仅在加性噪声激励下,系统的平均输入能量随强度D1的变化(α1=0.5,A2=α2=0.0)Fig.7 Average input energy as a function of intensity D1for the case of additive noise excitation(α1=0.5,A2=α2=0.0)

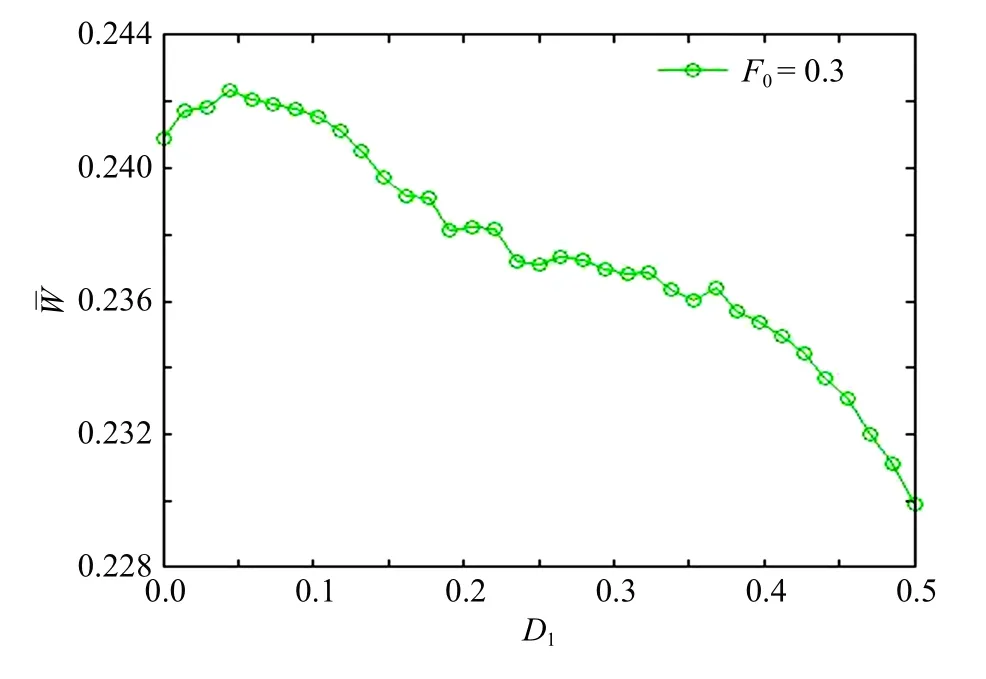
图8 在加性和乘性噪声共同激励下,系统的平均输入能量随强度D1的变化(α1=α2=0.5,A2=2.5)Fig.8 Average input energy as a function of intensity D1for the case of both additive and multiplicative noise excitations(α1=α2=0.5,A2=2.5)

图9 仅在加性噪声激励下,系统的平均输入能量随加性噪声转迁率α1的变化(A1=0.3,A2=α2=0.0)Fig.9 Average input energy as a function of transition rate of additive noise for the case of additive noise excitation(A1=0.3,A2=α2=0.0)

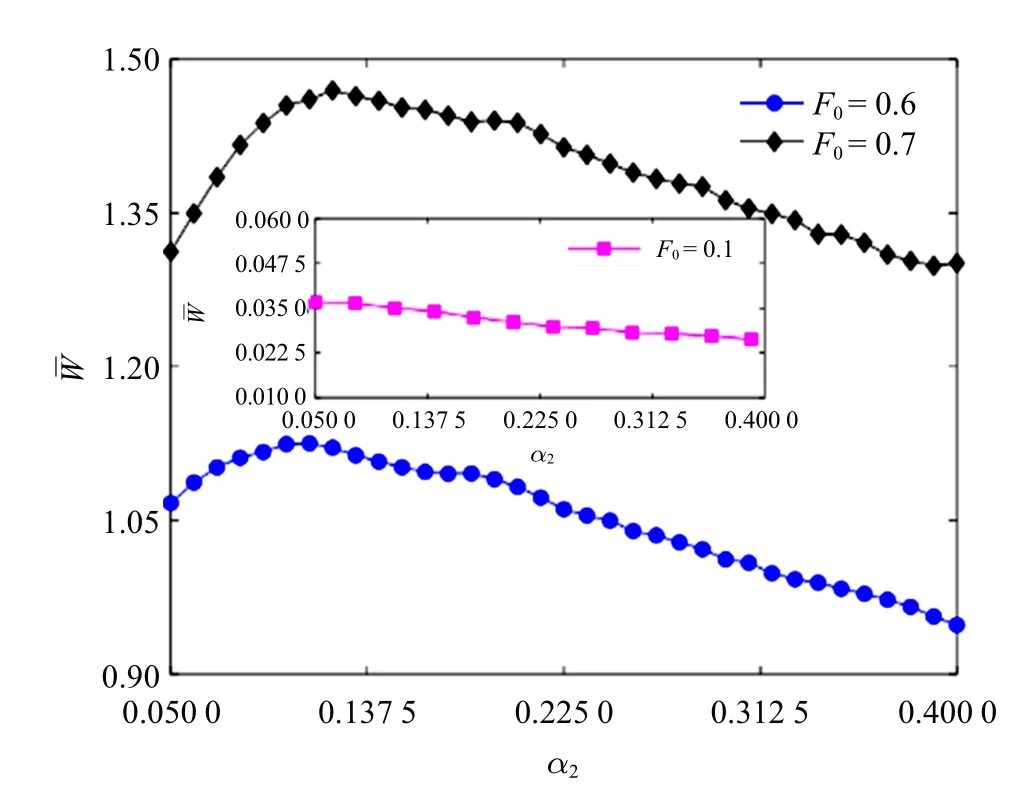
图10 仅在乘性噪声激励下,系统的平均输入能量随乘性噪声转迁率α2的变化(A2=3.0,A1=α1=0.0)Fig.10 Average input energy as a function of transition rate of multiplicative noise for the case of multiplicative noise excitation(A2=3.0,A1=α1=0.0)

图11 在加性和乘性噪声共同激励下,系统的平均输入能量随加性噪声转迁率α1的变化(A1=3.0,α2=0.5,A2=2.5)Fig.11 Average input energy as a function of transition rate of additive noise α1for the case of both additive and multiplicative noise excitations(A1=3.0,α2=0.5,A2=2.5)

3 结论

本文主要研究了由加性和乘性三值噪声激励下,二阶欠阻尼周期势系统中的非线性随机动力学.通过计算系统的联合稳态概率密度函数和瞬态概率密度函数,讨论了系统参数和外周期力振幅对联合概率密度函数的影响,显示了瞬态概率密度函数在一个周期内的演化过程.利用随机能量法研究了周期力和噪声对系统的平均输入能量的影响,揭示了系统的随机共振现象,发现存在适当的噪声强度和外周期力振幅使得平均输入能量曲线存在极大值,导致系统出现随机共振现象.在平均输入能量随加性噪声转迁率的变化规律中发现当周期力幅值较小时,出现了抑制共振的现象;平均输入能量随乘性噪声转迁率的变化中也出现了随机共振现象,但相比于加性噪声转迁率,未见抑制共振现象,说明乘性三值噪声和加性三值噪声对系统随机共振的影响是不同的.