三维空间直角坐标转换的Bursa模型抗差解法

陈再辉

三维空间直角坐标转换的Bursa模型抗差解法

陈再辉

（丽水市建设技术管理中心，浙江 丽水 323000）

对于空间直角坐标转换精度的研究主要是转换模型的选取和抗差估计理论的应用，通过各种模型和算法提高转换参数的解算精度。针对空间直角坐标转换中的布尔萨（Bursa）模型的严密公式，给出了模型的抗差求解方法和具体的解算步骤，解算过程更为严谨。使用常用的几种权函数进行模型参数的抗差解算，对其求解参数的收敛速度进行比较分析。通过具体实例验证了方法的有效性和可靠性。

空间直角坐标；布尔萨模型；抗差估计；粗差

0 引言

生产实际中经常需要进行数据的坐标转换：一种是同一椭球不同坐标形式的转换，另一种是不同椭球之间的坐标转换。空间直角坐标系是坐标转换中连接不同基准的桥梁，利用两个坐标系的两套重合点坐标求取转换参数，进而进行坐标系统转换。公共点坐标的精度直接影响转换参数的求解精度，对于提高空间直角坐标转换精度的研究主要是转换模型[1-3]和抗差估计[2-5]算法。文献[1]提出了空间直角坐标的统一转换模型，采用正交普罗克鲁斯忒斯（Procrustes）分析，对模型进行求解,但是正交Procrustes分析构建矩阵、分解矩阵的过程比较繁琐。文献[2]针对大旋转角坐标转换的模型线性化复杂、计算量大等问题，并顾及数据粗差对计算结果的影响进行了研究。文献[3]对三维坐标转换的高斯-赫尔默特模型，采用牛顿-高斯迭代算法时，模型不受旋转角度大小限制的问题进行了研究。

当观测数据含有粗差时，如何通过算法将其纠正，保证模型参数解算的可靠性，国内外研究者进行了大量的相关研究，主要是粗差探测与剔除和抗差估计算法[2-5]。文献[2-3]使用了抗差估计的理论，稳健性良好，但是存在大量的矩阵运算。文献[4]根据稳健估计理论,对有粗差的公共点以重新定权的方式降低其在解算中的作用。抗差估计可以有效地剔除和纠正粗差数据的影响，文献[5]将抗差估计理论用于布尔萨（Bursa）参数的求解，但使用的是简化了的Bursa公式，忽略了二阶以上的项[5-6]。本文使用Bursa七参数转换的严密公式进行求解和分析，并对常用的几种权函数的收敛速度进行比较和分析。

1 Bursa转换模型[6]

Bursa坐标转换模型为

取

式中下角标C和O分别表示转换值和已知值，则误差方程式为

矩阵形式为

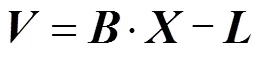
法方程为

其解为

2 Bursa模型抗差解[7]

转换参数抗差解的+1步迭代表达式为

式中

抗差模型的计算步骤：

3 算例分析

取浙江省丽水市莲都区某区域两套重合点的空间直角坐标作为起算数据，总共27个点，随机取3个点（1号点、26号点和27号点）作为检核点，其余24个点作为起算数据进行解算。随机取两个点（15号点、16号点）模拟粗差数据，在这两个点的、、坐标分量上加入粗差，点位分布示意图如图1所示。

图1 点位分布示意

表1 7参数模型解算结果表

表2 检验点1号点、26号点、27号点坐标差值 单位：mm

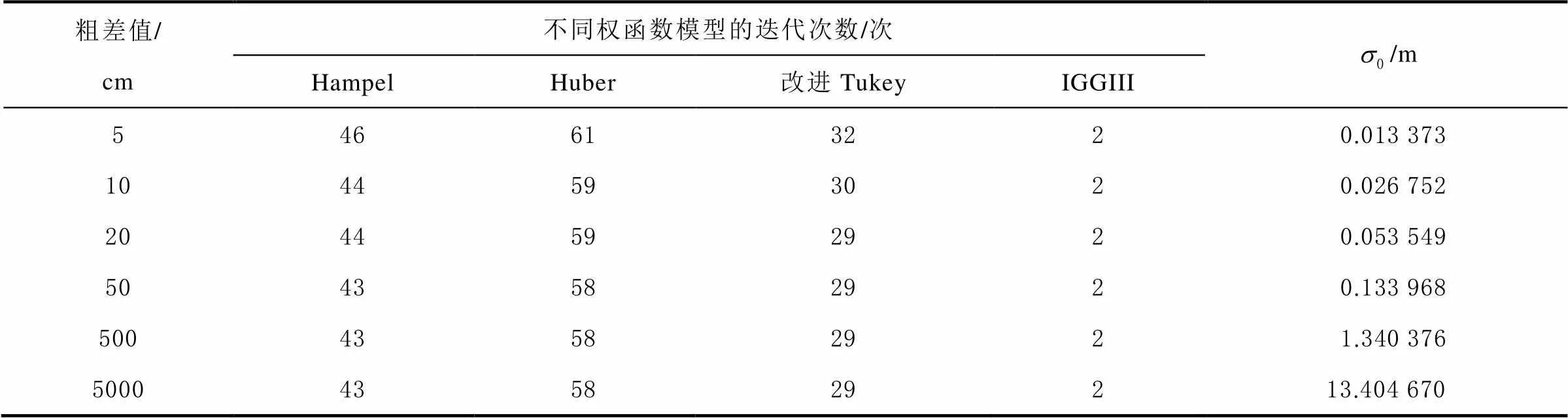
表3 加入不同粗差值并使用不同权函数的结果

图2 无粗差时LS模型解算结果的残差

图3 含粗差时抗差估计方法解算结果的残差

对于不同数值的粗差，同一权函数模型解算的迭代次数变化较小，当加入的粗差数值不断减小时，迭代次数增大。对于相同数值的粗差，使用IGGIII模型权函数时迭代次数最少，函数收敛速度最快，Huber模型权函数迭代次数最多，函数收敛速度最慢，其中使用IGGIII模型权函数时，迭代次数受粗差大小的影响较小。求解过程中发现，使用Tukey模型权函数时，系数矩阵秩亏，使用改进的Tukey模型权函数解算成功，达到预期的目的。

4 结束语

本文针对不同基准坐标转换中的空间直角坐标转换的Bursa模型的严密公式，给出了模型的抗差求解方法和具体解算步骤，解算过程更为严谨。当原始数据含有粗差时，使用抗差估计方法可以直接对粗差进行剔除和纠正，保证了解算的可靠性。在使用抗差模型求解转换参数时，对于使用不同的权函数时的收敛速度进行了比较和分析。

[1]吴继忠, 王安怡. 空间直角坐标转换的统一模型[J]. 大地测量与地球动力学, 2015, 35(6): 1046-1048.

[2]李国琴, 田林亚, 郭英起, 等. 基于罗德里格矩阵的抗差迭代坐标转换算法研究[J]. 测绘工程, 2018, 27(3): 11-15.

[3]刘超, 王彬, 赵兴旺, 等. 三维坐标转换的高斯-赫尔默特模型及其抗差解法[J]. 武汉大学学报(信息科学版), 2018, 43(9): 1320-1327.

[4]郭英起, 黄声享, 曹先革. 基于稳健估计的高精度坐标转换参数解算方法[J]. 测绘工程, 2008, 17(6): 6-8.

[5]倪飞, 崔桂官. 空间直角坐标系统转换的抗差算法研究[J]. 海洋测绘, 2011, 31(6): 28-30.

[6]孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2006: 44-45.

[7]杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993: 273-275.

Bursa model robust solution for cartesian coordinate transformation in three-dimensional space

CHEN Zaihui

（Lishui Construction Technology Management Center, Lishui，Zhejiang 323000, China）

The research on the accuracy of space rectangular coordinate transformation is mainly the selection of transformation model and the application of robust estimation theory. Through various models and algorithms, the accuracy of transformation parameters is improved. Aiming at the rigorous formula of Bursa model in space rectangular coordinate transformation, this paper gives the model's robust solution method and specific solution steps, and the solution process is more rigorous. Several commonly used weight functions are used for robust calculation of model parameters, and the convergence speed of their solution parameters is compared and analyzed. The effectiveness and reliability of the method are verified by specific examples.

spatial Cartesian coordinates; Bursa model; robust estimation; gross error

P228

A

2095-4999(2021)02-0118-04

陈再辉.三维空间直角坐标转换的Bursa模型抗差解法[J].导航定位学报,2021,9(2): 118-121.（CHEN Zaihui.Bursa model robust solution for cartesian coordinate transformation in three-dimensional space[J].Journal of Navigation and Positioning,2021,9(2): 118-121.）

10.16547/j.cnki.10-1096.20210219.

2019-12-03

陈再辉（1981—），女，陕西富平人，硕士，高级工程师，研究方向为GIS和GNSS。