从课前到课后，充分发挥作业的评价功能

陈新涛 张明红

摘要：教學（学习活动的设计、组织和引导）需要以了解学生的学习情况为基础。广义的作业是指围绕教学目标展开的学习活动。发挥作业的评价功能，应该通过作业的设计和学生完成情况，采集和分析学生的学习情况（信息、数据），从而诊断学习问题，做出教学应对;可在课前、课中、课后三个不同的时间段展开。

关键词：以学定教;作业评价;《间隔排列》

学习是一个以已有知识和经验为基础的主动建构和迁移的过程。教学（学习活动的设计、组织和引导）需要以了解学生的学习情况为基础。广义的作业是指围绕教学目标展开的学习活动。教师通常更重视作业的教学功能，而忽视作业的评价功能。发挥作业的评价功能，应该通过作业的设计和学生完成情况，采集和分析学生的学习情况（信息、数据），从而诊断学习问题，做出教学应对。发挥作业的评价功能，可在课前、课中、课后展开。三个时间段的作业评价活动环环相扣、各有侧重。下面以苏教版小学数学三年级上册《间隔排列》一课为例来说明。

一、课前作业评价：指导课堂教学

本节课主要涉及两个知识点：理解间隔排列现象（概念），探索其中的规律（数量关系）。因此，我们设计了两个课前作业：

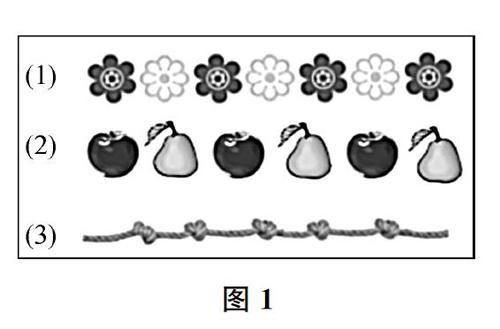
1.生活中你见过像图1中三幅图这样的现象吗？

举个例子：_________________________________________。

2.看第1题的第三幅图，把6根短绳连在一起，要打（）个结;如果一根绳子上打了12个结，需要（）根短绳。

课前作业第1题提供了三幅情境图，先不说明是间隔排列现象，而追问学生在生活中是否见过这样的现象，并要求学生举例说明对此现象的理解，旨在了解学生对间隔排列现象是否有认识以及认识到了什么程度。

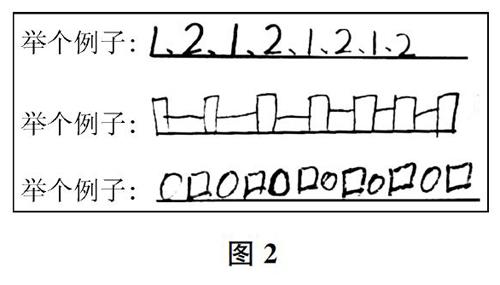
对于第1题，全班40位学生，除了3位没有举例以外，其他都能正确举例表达对间隔排列现象的认识，正确率为92.5%。而学生举例的表征方式并不相同：有的用数字符号，有的用几何图形（典型例子如图2）。由此可知，学生对间隔排列现象已经比较熟悉，且举例时能够用自己喜欢的方式表征，但可能停留在类比迁移的感性认识层面，而未达到抽象概括的理性认识层面。

根据第1题的完成情况，我们设计如下学习活动，直接、快速地引导学生通过观察、比较，抽象出间隔排列的本质属性，即“两种物体”和“一个隔着一个”，从而更加理性地认识间隔排列。

如图3，这三幅图的排列有什么共同点？

课前作业第2题针对绳子打结的情境图，先提出一个“看图数数”的简单问题，给学生提供一个“脚手架”;再提出一个反向思考的“想象推理”的复杂问题，主要考查学生对间隔排列规律的理解程度以及运用能力。

对于第2题，全班40位学生，只有4位出错，正确率为90%。出错的4位学生都错在后面一空，其中，2位学生完全不会做，瞎猜了答案（如图4）;2位学生大概记得绳结数与短绳数相差1，但是把谁比谁多1的关系弄反了（如图5）。由此可知，学生对间隔排列规律有一定的认识，但可能是模糊的记忆、直觉的猜想，而不是清晰的理解、逻辑的推理。

根据第2题的完成情况，我们设计如下学习活动，引导学生自主探索、合作交流，经历、体验间隔排列规律的“再发现”过程，从而清晰地理解、逻辑地推出间隔排列规律。

同桌两人分工，各选择下面两类中的一类进行研究，在所选的类别后打“√”，把研究结果填写在表1中。

两端物体相同（ ）;两端物体不同（ ）。

（2）思考：为什么会有这个规律？

（3）把你的发现和想法与同桌交流。

二、课中作业评价：做好即时反馈

引导学生完成上面两个学习活动后，我们设计了两个课中作业：

1.（1）请你用图形或符号创造一个间隔排列的作品。

（2）有人说锯木头问题中也有间隔排列，你怎么看？画图解释。

2.串珠子时，有7个红珠子，4个蓝珠子，6个绿珠子，7个黄珠子，100个黑珠子。

（1）两种珠子都用完，选择哪种珠子能跟红珠子组成间隔排列？

（2） 如果把100个黑珠子全部用完，需要多少个红珠子？

课中作业第1题是课前作业第1题和课上第一个学习活动的延伸，主要是在学生认识间隔排列现象后，让学生用自己的方式表达个性化理解，重在建构“多元表征性理解”;在学生认识间隔排列概念后，让学生解释一个不太“标准”（比较“特殊”）的间隔排列，重在促进“深度本质性理解”。它们可以进一步考查学生对间隔排列现象和概念的理解程度。

课中作业第2题是课前作业第2题和课上第二个学习活动的延伸，主要是在学生理解间隔排列规律后，让学生综合运用规律解决较为开放（需要考虑多种可能的情况）的实际问题;同时，采用文字的方式表达，没有图形表征和操作活动，让学生发挥想象，抽象思考。第（1）小题可以直接运用规律解答，也可以画图辅助解答;第（2）小题只能直接运用规律解答。它们可以进一步考查学生对间隔排列规律的理解程度以及运用能力。

课上，对于课中作业第1题的第（1）小题，教师在巡视中发现：创造间隔排列作品时，有的学生用具体的实物图形表征，有的学生用抽象的几何图形表征，还有的学生用更抽象的符号及文字、字母表征;有的学生让两端的物体相同，有的学生让两端的物体不同（典型例子如图6）。此外，还有一位学生很特别，他创作的间隔排列作品如下：○○□□○○□□○○□□。显然，这一作品看上去不是本节课所学的一一间隔排列，但实际上，如果把两个○和两个□分别圈起来看作一组，就符合一一间隔排列的特征了。对此，教师一方面展示各类学生作品的典型代表（如图6），引导点评，建构学生的“多元表征性理解”;另一方面展示上述特别的学生作品，引发讨论，拓宽和加深学生对间隔排列现象和概念的理解。

对于课中作业第1题的第（2）小题，教师在巡视中发现：解释锯木头的问题时，有的学生画出一段木头和其中的分割线，表示锯开后的木头和锯开处的空隙两种“物体”的间隔排列，这是一种深入本质的理解;有的学生画出长短不一的两种木头的间隔排列，这是一种比较个性化的理解。对此，教师展示各类学生作品的典型代表，引导点评，促进学生的“深度本质性理解”。

对于课中作业第2题，教师在巡视中发现：学生基本上都能正确回答问题。因此，教师只简单地请一位学生展示、讲解了解题过程。

课后，对于课中作业第1题的第（1）小题，通过统计发现：所有学生都正确创造出间隔排列的作品（上述特别的间隔排列作品也被认为在某种程度上是正确的），其中，50%的学生用几何图形表征，17%的学生用实物图形表征，20%的学生用符号表征，13%的学生用文字或字母表征。相比于课前作业第1题的完成情况，正确率的提高和表征方式的丰富，都能说明学生对间隔排列现象和概念有了更好的理解。

对于课中作业第1题的第（2）小题，通过统计发现：94%的学生用自己的方式正确表达了对锯木头问题中间隔排列的理解;6%的学生无法理解锯木头问题中的间隔排列。这说明，在更高的抽象程度上认识间隔排列现象和概念是本节课教学的一个难点。针对6%的学生无法理解锯木头问题中的间隔排列，教师可以通过个别辅导以及设计针对性作业（比如下述课后作业第3题），帮助这些学生理解。

对于课中作业第2题，通过统计发现：学生的正确率确实为100%。相比于课前作业第2题的完成情况，题目难度的增加和正确率的提高，都能说明学生对间隔排列规律有了更好的理解和掌握。

三、课后作业评价：启发补偿教学

课堂教学结束后，我们设计了三个课后作业：

1.用4个□和4个○设计间隔排列，你能设计出几种？比比看谁设计的多。

2.马路边一共有25根电线杆，每两根电线杆之间有一块广告牌，一共有（）块广告牌。

3.“王小明从一楼爬到五楼花了20分钟，从一楼爬到二楼花了多少分钟？”有人说花了4分钟，有人说花了5分钟，你觉得呢？试用今天学习的知识解释。

课后作业第1题是课前作业第1题、课上第一个学习活动和课中作业第1题第（1）小题的延伸，主要是让学生在一定的限制条件下设计尽可能多的（自然要有比较特别的）间隔排列，进一步考查学生对间隔排列现象和概念的理解程度。

课后作业第2题是课前作业第2题和课上第二个学习活动的简单延伸，主要是让学生运用规律解决较为封闭（只需考虑一种确定的情况）的实际问题，再次考查学生对间隔排列规律的理解程度以及运用能力。

课后作业第3题则是课中作业第1题第（2）小题和课后作业第2题的综合延伸，主要是让学生发现另外一个不太“标准”（比较“特殊”）的间隔排列;然后，运用相应的规律解决问题（完成数学建模和解模）。这可以进一步考查学生对间隔排列现象和概念的理解程度以及对间隔排列规律的理解程度和运用能力。

对于课后作业第1题，全班40位学生都设计出了两种线形一一间隔排列，其中，4位学生还设计出了一种环形一一间隔排列，2位学生还设计出了两种线形两两间隔排列。相比于课中作业第1题第（1）小题的完成情况，设计形式的再次创新，能说明学生对间隔排列现象和概念又有了更好的理解。对此，教师可以通过集体展示以及设计针对性作业，让所有学生认识到环形一一间隔排列是一种特殊的间隔排列，并探究其中的规律;通过个别辅导，帮助设计出线形两两间隔排列的学生理解，只有把两个□和两个○分别圈起来看作一组，才符合一一间隔排列的特征。

对于课后作业第2题，学生的正确率仍然为100%。这在我们的预料（或者说期待）中，说明学生对间隔排列规律理解得比较充分、掌握得比较牢固。

对于课后作业第3题，全班40位学生，有4位出错，正确率为90%。出错的4位学生都认为从一楼到五楼的距离是从一楼到二楼距离的5倍，于是用20除以5，得到从一楼爬到二楼需要4分钟。答对的学生有的用文字解释，有的用图形解释，都能发现楼梯和楼层两种“物体”的间隔排列，从而运用相应的規律解决问题。爬楼问题中的典型错例进一步说明，在更高的抽象程度上认识间隔排列现象和概念是本节课教学的一个难点。对此，教师可以通过个别辅导以及设计针对性作业，帮助出错的学生理解爬楼问题中的间隔排列。如果这些学生还是难以理解，教师应该尊重个体差异，遵循认知发展规律，保持耐心，循序渐进，关注、了解学生思维从具体到抽象（数学建模）的过程，等待、促进这些学生抽象逻辑思维的进一步发展——毕竟他们才三年级。

*本文系江苏省南京市教育科学“十三五”规划2018年度重点联系课题“回归本质：‘至理数学的教学主张建构与实践研究”（编号：L/2018/029）、江苏省中小学教学研究第十三期重点自筹课题“以理学案为载体的‘至理数学课例群建设研究”（编号：2019JK13ZB08）的阶段性研究成果。