考虑惯容的颗粒阻尼器等效力学模型及其受控结构稳态解研究

黄绪宏，许维炳，王 瑾，闫维明，陈彦江

(北京工业大学工程抗震与结构诊治北京市重点试验室，北京 100124)

颗粒阻尼器最早由冲击减振器发展而来，用于涡轮机叶片的减振研究中[1]，然而由于单颗粒冲击阻尼器在减振过程中会产生较大的噪声及其对设计参数的敏感性限制了其在实际中的应用。多颗粒阻尼器(Multi-particle damper, M-PD)的引进改进了单颗粒冲击阻尼器冲击力大及鲁棒性差的缺点。具有减振效果好、作用频带宽、成本低、布置灵活、使用寿命长等优点，因而在航空及机械振动控制领域得到了广泛的研究与应用[2-3]，其在土木工程领域中的应用与发展近年来也得到了关注与重视[4-6]。

Papalou 和Masri[7]用钨粉代替传统的单颗粒冲击阻尼器，以单层框架结构作为研究对象在宽频随机激励下进行振动台试验研究，重点分析了质量比、容器尺寸、激励水平等不同因素对颗粒阻尼器耗能特性的影响。Saeki[8]在水平简谐激励下以单自由度结构(Single-degree of freedom, SDOF)作为研究对象，基于试验研究及离散单元法研究了相关参数对M-PD 减振性能的影响，结果表明颗粒质量和尺寸对颗粒阻尼器性能影响显著。许维炳和王瑾[9-10]针对M-PD 在土木工程领域中的应用进行了详细的研究，并以实际高架连续桥梁缩尺模型及三层框架缩尺模型作为研究对象，进行了地震荷载作用下减震效果分析。鲁正等[6,11]基于试验研究及离散单元法对地震荷载及风荷载作用下M-PD 减振性能进行了详细分析，验证了M-PD 减振效果。M-PD 试验研究初步探索了其减振性能及机理，为M-PD 理论模型建立及工程应用提供了参考及试验依据。

M-PD 具有复杂的非线性特性，合理有效的力学模型对于进一步认识M-PD 及实际工程应用具有重要意义。Papalou 和Masri[7]基于等效前后剩余体积及质量相同的原则将M-PD 等效为单颗粒阻尼器，并基于试验研究验证了模型的合理性。许维炳[9]将调频型颗粒阻尼器(Particle tuned mass damper, PTMD)等效为双调谐质量阻尼器，在试验验证基础上进行了理论分析并提出了简化设计方法。鲁正等[12]参考Papalou 提出的等效原则将多颗粒等效为单颗粒，并基于接触单元法建立了PTMD 等效力学模型，通过地震作用下结构响应试验验证了等效方法的合理性，最后基于该等效方法也给出了PTMD 的简化设计方法。王宝顺等[13]在考虑滚动摩擦效应的基础上提出了对应等效单颗粒力学模型，并进行了参数影响分析。为考虑颗粒之间相互作用对减振效果的影响，Huang 等[14]提出了等效连体颗粒质量模型。值得注意的是：在机械领域颗粒阻尼器的振动以高频振动为主，阻尼颗粒的速度很大；而土木工程结构相比机械振动频率低，阻尼颗粒与腔体之间的相对速度一般小于5 m/s[15]。在颗粒未发生堆积时，阻尼颗粒在运动过程中以滚动为主，且考虑颗粒之间相互作用后的颗粒在振动过程中运动状态更加复杂。颗粒滚动可能会引起颗粒群额外的惯性属性，甚至会因此影响M-PD 减振性能及减振机理。

对于等效单颗粒力学模型而言，由于其构造简单，且冲击单颗粒阻尼器相关理论分析成果可以被应用到该模型的理论分析中，因此具有较好的推广性。假设颗粒发生周期2 次碰撞，Masri 等[16-17]分别给出了单自由度结构及多自由度结构稳态解析解，并通过求解误差传递矩阵对周期运动的稳定性进行了讨论。Popplewel 等[18]在周期多次碰撞理论分析基础上指出当发生周期2 次碰撞时减振效果最优，并对最优碰撞间距进行了理论推导[19]。闫维明等[20]在周期运动解析基础上推导得到了最优碰撞间距，并对并联式单向单颗粒阻尼器进行了优化设计。

鉴于此，在不考虑颗粒堆积的前提下，本文拟通过引入惯容器来考虑颗粒群滚动及其他非线性影响因素对多颗粒阻尼器减振机理的影响，建立具有惯容属性的多颗粒阻尼器等效单颗粒力学模型。结合阻尼颗粒的运动状态，分别进行未碰撞时及发生碰撞后MPD-SDOF 系统的响应分析，重点讨论了惯容系数q 对未碰撞时位移放大系数及周期2 次碰撞稳态解析解的影响，并分别基于数值仿真分析及振动台试验研究对理论解析的合理性进行验证。考虑惯容影响后的理论分析结果可为土木工程领域中多颗粒阻尼器减振机理分析及优化设计提供理论基础。

1 考虑惯容属性的多颗粒阻尼器—单自由度结构力学模型

多颗粒阻尼器通过运动过程中颗粒之间及颗粒与容器之间碰撞和摩擦，消耗、存储并传递振动能量，藉此以达到减轻结构振动的目的。多颗粒在运动过程中表现出很强的非线性特性，因此进行带有多颗粒阻尼器结构的精确分析是相当困难的。研究表明，在颗粒未发生堆积时，多颗粒可以等效为单颗粒从而建立多颗粒阻尼器等效力学模型[21,7]。多颗粒等效为单颗粒的原则为：1)颗粒在等效前后的质量相等；2)颗粒在等效前后颗粒材料特性及形状不发生变化；3)等效前后颗粒阻尼器内空隙与腔体体积比一致。

与机械领域相比，土木工程领域结构振动以水平振动为主，结构振动具有低幅低频的特性，颗粒在运动过程中以滚动为主，且多颗粒在振动过程中运动状态更加复杂。然而目前颗粒阻尼器力学模型建立过程中，忽略了颗粒滚动对减振机理的影响。借鉴车辆工程中加速阻力的概念[22]，假设颗粒在外荷载作用下(简谐激励或地震动激励)相互独立滚动，则颗粒群对应加速阻力FJ可由下式表示：

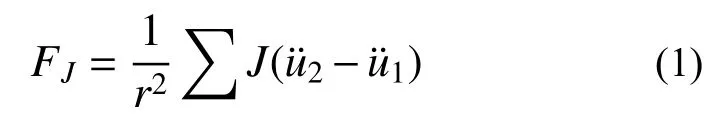
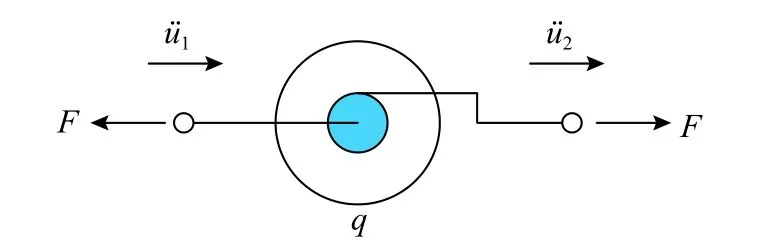
图 1 两端点惯性元件—惯容Fig.1 Two-terminal inertial element—inerter

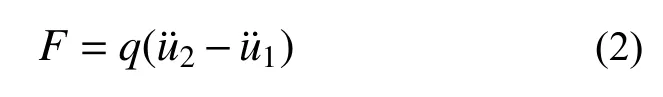
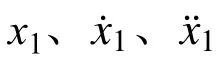
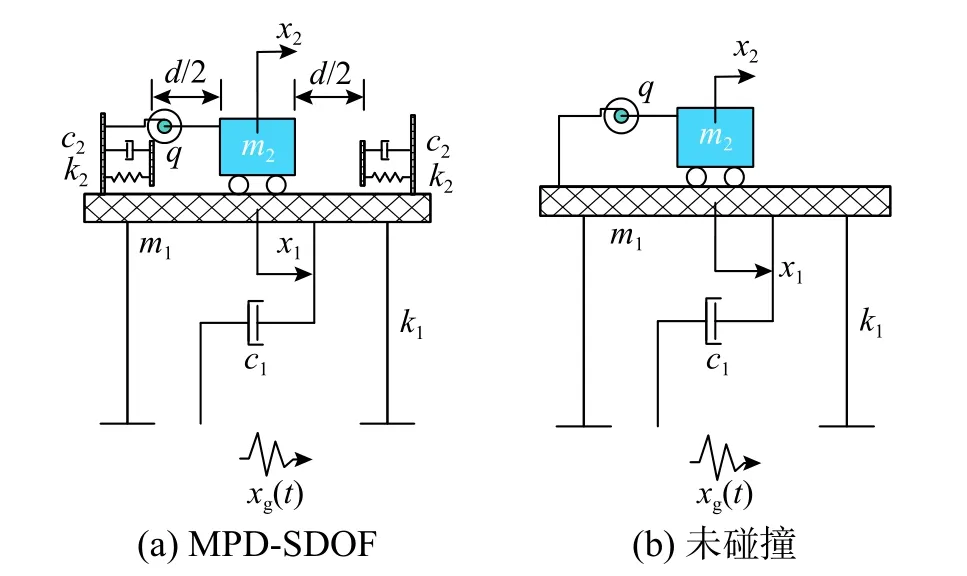
图 2 力学模型Fig.2 Mechanical model

2 未碰撞时结构响应分析

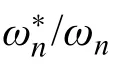
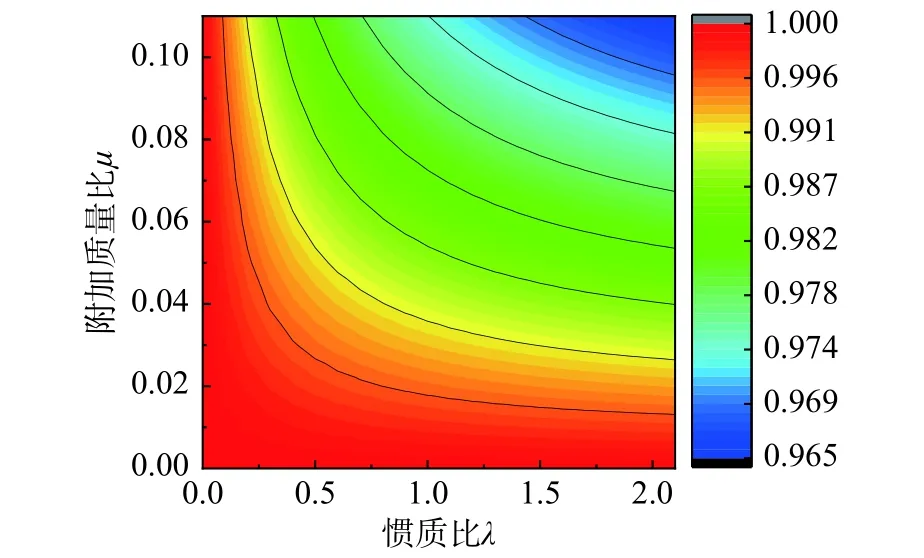
图 3 考虑惯容后 随μ及λ 变化规律Fig.3 Change rule of with μ and λ after considering q

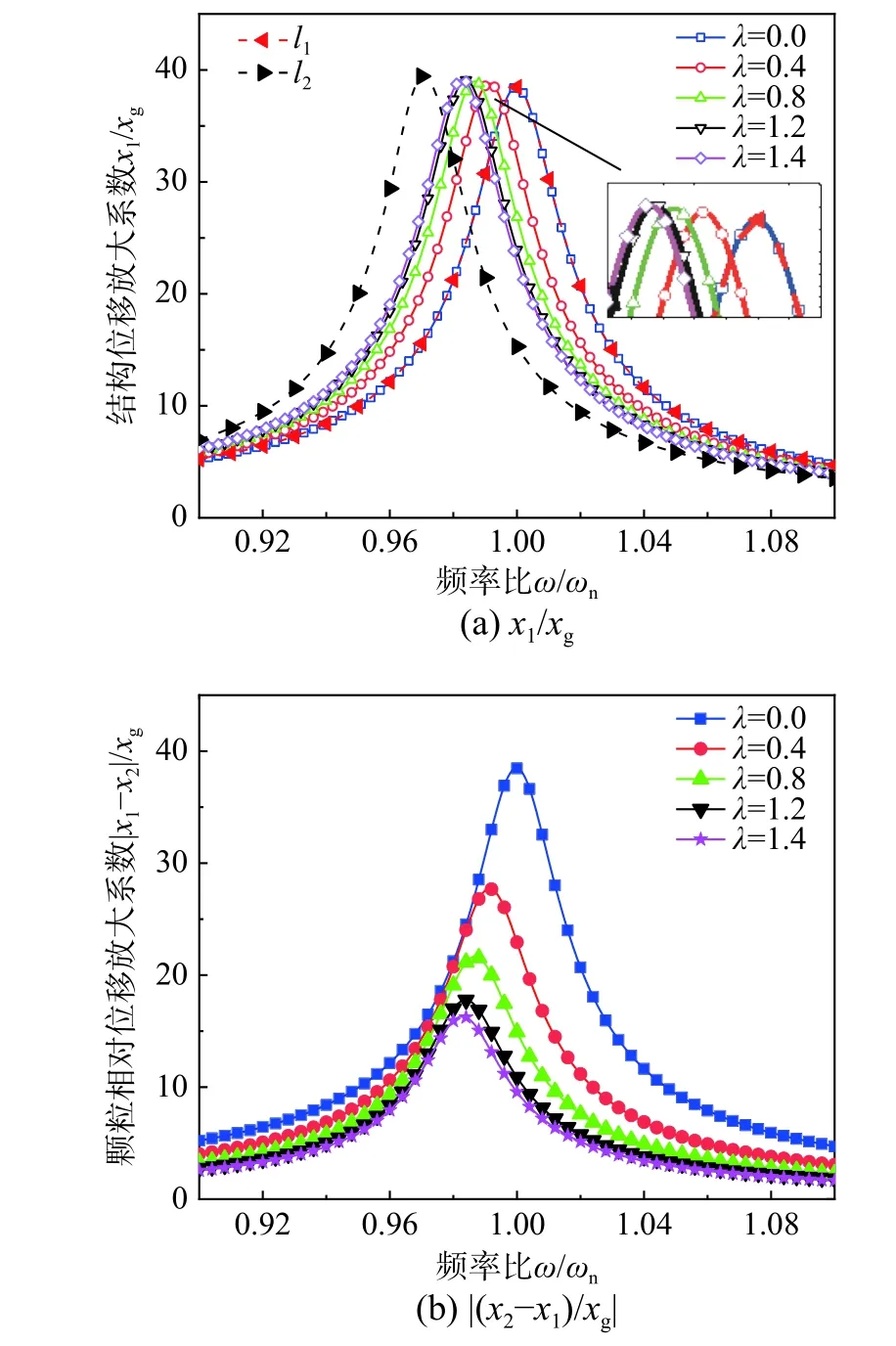
图 4 位移放大系数频响曲线Fig.4 Frequency response curve of displacement amplification coefficient

3 周期2 次碰撞稳态解析解

研究表明，简谐激励下当颗粒发生稳定周期2 次碰撞时减振效果最优[27]。Masri 等[16-17]分别给出了单自由度结构及多自由度结构稳态解析解，并通过数值仿真试验验证了解析解的准确性。与冲击阻尼器相比，考虑颗粒群惯容属性后稳态周期2 次碰撞的稳态解析解发生改变。为了从理论解析的角度上评价颗粒阻尼器减振机理及能量变化规律，本文将颗粒与结构的振动过程划分为多个非碰撞过程及碰撞过程分别建立运动微分方程，以此得到周期2 次碰撞稳态解析解。

3.1 MPD-SDOF 运动微分方程

当阻尼颗粒不与结构发生碰撞时，由式(3)得未碰撞时体系运动方程为：

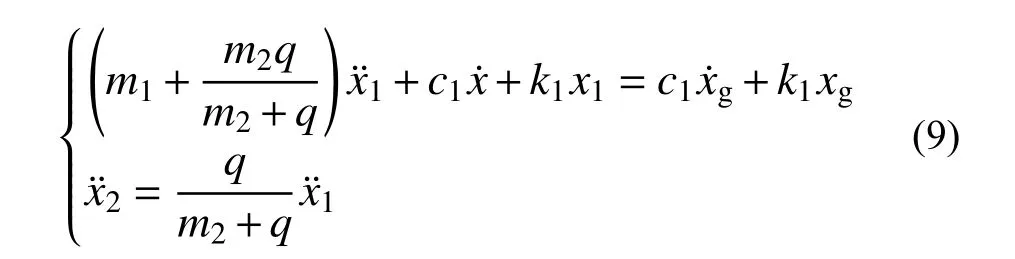
其中：F0为对应外部激励荷载幅值；ω 为外部荷载激励频率；假设颗粒发生稳态周期运动后，某次周期运动初始时刻颗粒位于容器左侧，φ 为对应初始时刻外部激励荷载初始未知相位角，t 为稳定后简谐激励作用的时间；meq为等效质量。则对应未碰撞时MPD-SDOF 运动位移关于时间的解析表达式如下所示：

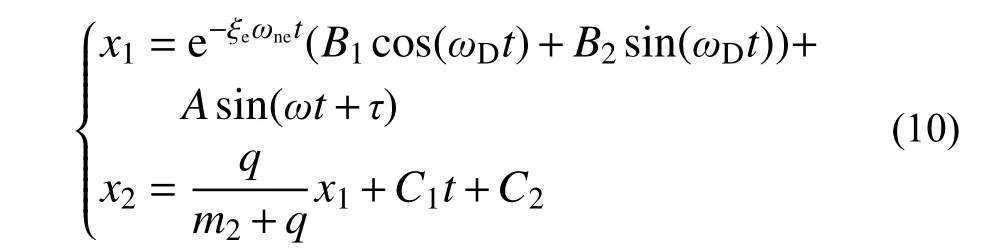
当阻尼颗粒与结构发生碰撞时，由于碰撞接触时间短且碰撞为正碰撞，可以用恢复系数e 表示碰撞前后主体结构及阻尼颗粒的速度跳跃关系[16]。由动量交换及碰撞恢复系数定义可知碰撞前后主体结构及阻尼颗粒的速度关系如下所示：

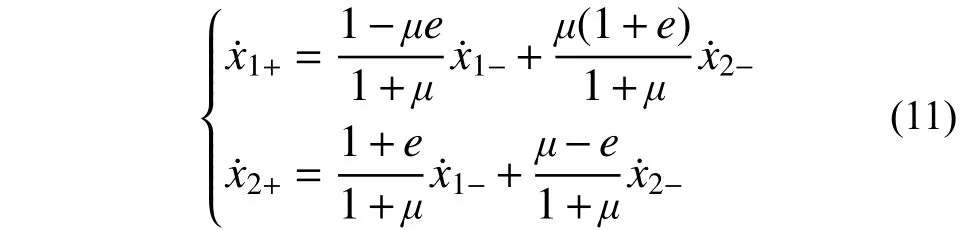
3.2 周期2 次碰撞稳态解析解的边界条件

由文献[16]分析可知，当MPD-SDOF 发生对称2 次碰撞稳定周期运动后，体系运动状态关于平衡状态对称，即颗粒及单自由度结构的周期运动位移-速度相轨迹是相对平面原点对称的一条封闭曲线，如图5 所示。

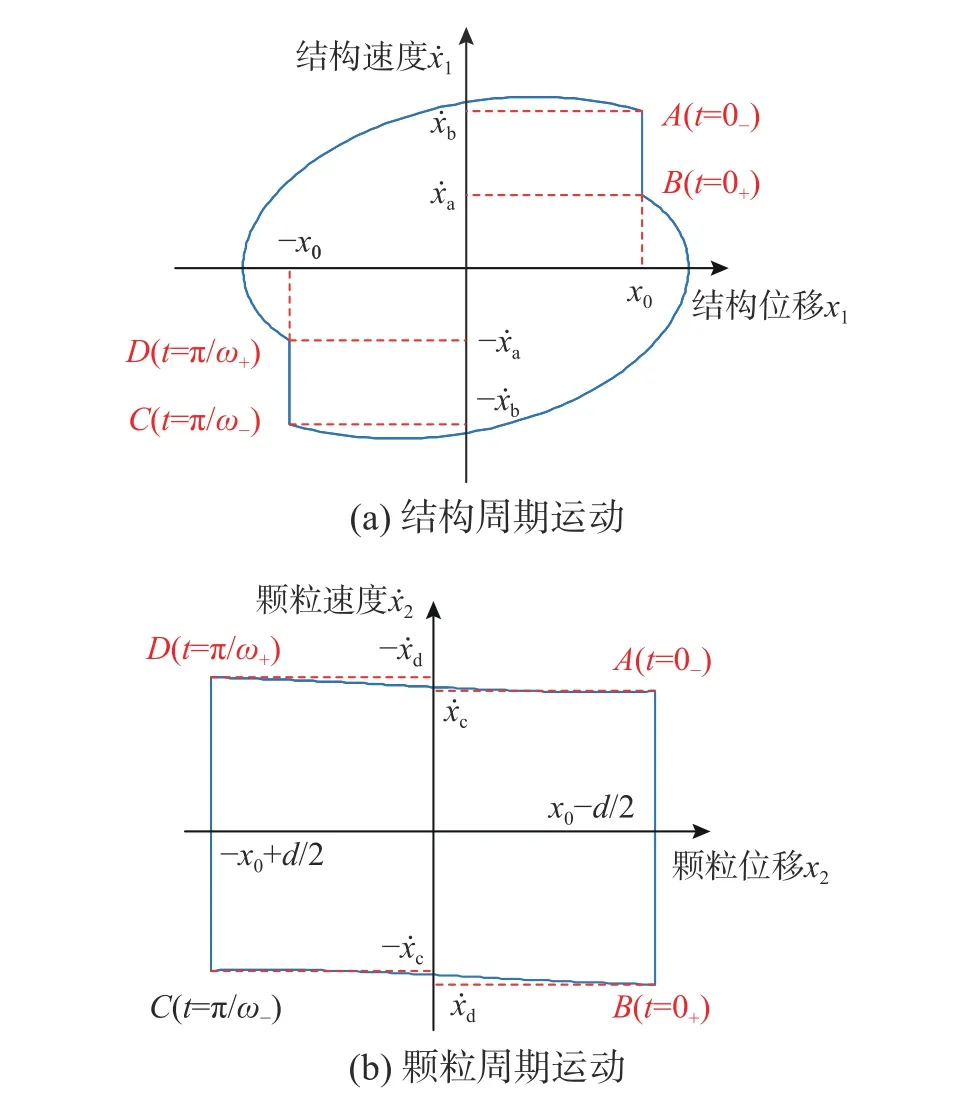
图 5 MPD-SDOF 位移-速度相位图Fig.5 Phase diagram of MPD-SDOF

假设图5 为MPD-SDOF 开始稳态运动的一个完整运动周期。A—B 段表示第一次碰撞过程主体结构及阻尼颗粒的运动状态，B—C 段表示第一次碰撞后非碰撞阶段主体结构及阻尼颗粒运动状态，C—D 段表示第二次碰撞过程主体结构及阻尼颗粒的运动状态，D—A 段表示第二次碰撞后非碰撞阶段主体结构及阻尼颗粒运动状态。其中，A 点表示第一次碰撞前的时刻(t=0-)，B 点表示第一次碰撞后的时刻(t=0+)，C 点表示第二次碰撞前的时刻(t=(π/ω)-)，D 点 表 示 第 二 次 碰 撞 后 的 时 刻(t=(π/ω)+)。则对应MPD-SDOF 稳态运动边界条件如下所示。

1) 第一次碰撞对应体系运动状态边界条件为：

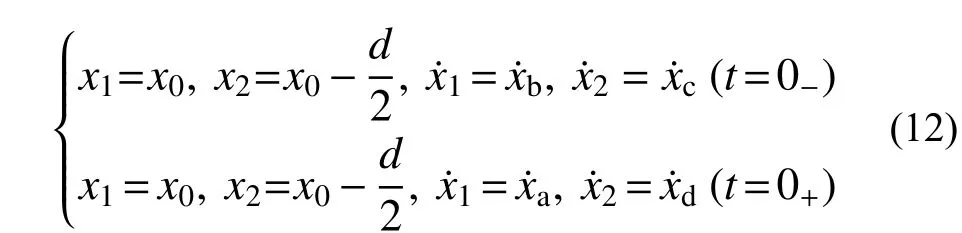
2) 第二次碰撞对应体系运动状态边界条件为：

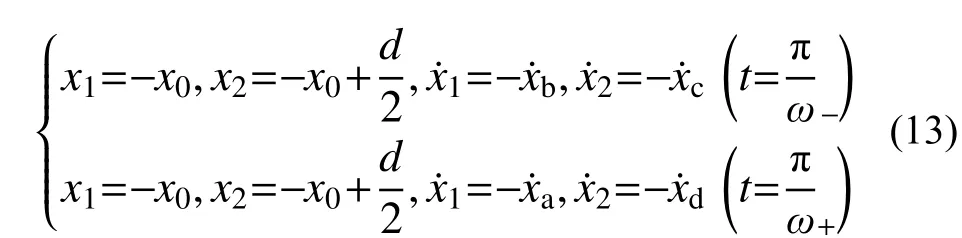
3.3 周期2 次碰撞稳态解析解求解

1) 由第一次碰撞状态边界条件式(12)及碰撞前后主体结构及阻尼颗粒速度关系式(11)可得：

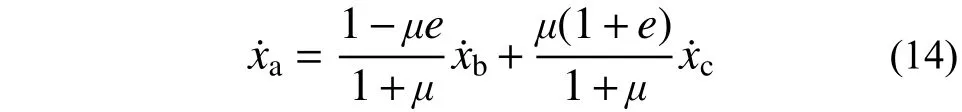
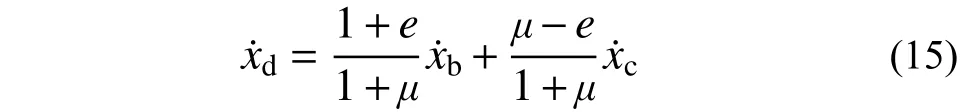
由式(10)得运动过程中颗粒运动速度为：

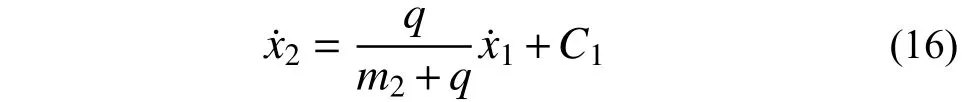
由式(16)及B—C 段颗粒速度边界条件得：

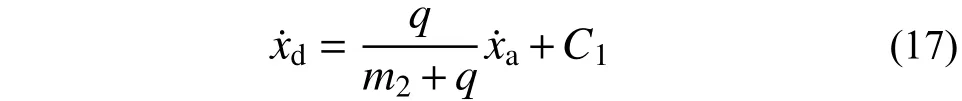
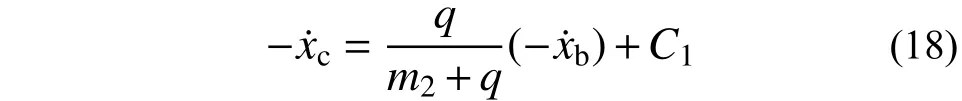
联立式(14)、式(15)、式(17)、式(18)可得单自由度结构及颗粒速度边界条件关于待定参数C1的解：

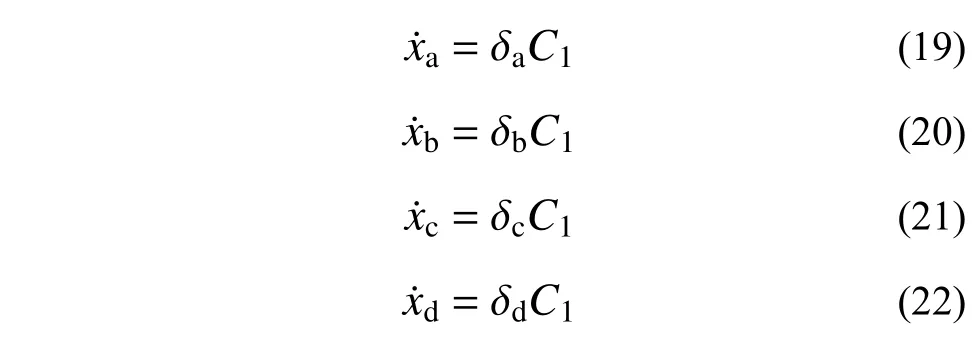
式中，δa、δb、δc、δd是关于e、m2、q、μ的常数。

2) 由半个运动周期内颗粒运动位移为2x0-d 得：

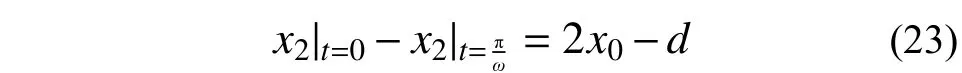
将式(10)代入式(23)得：

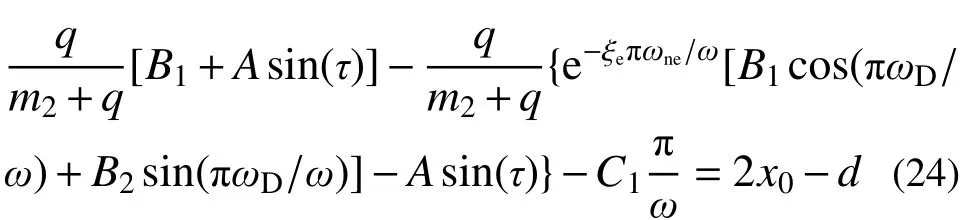
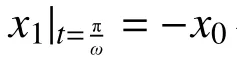
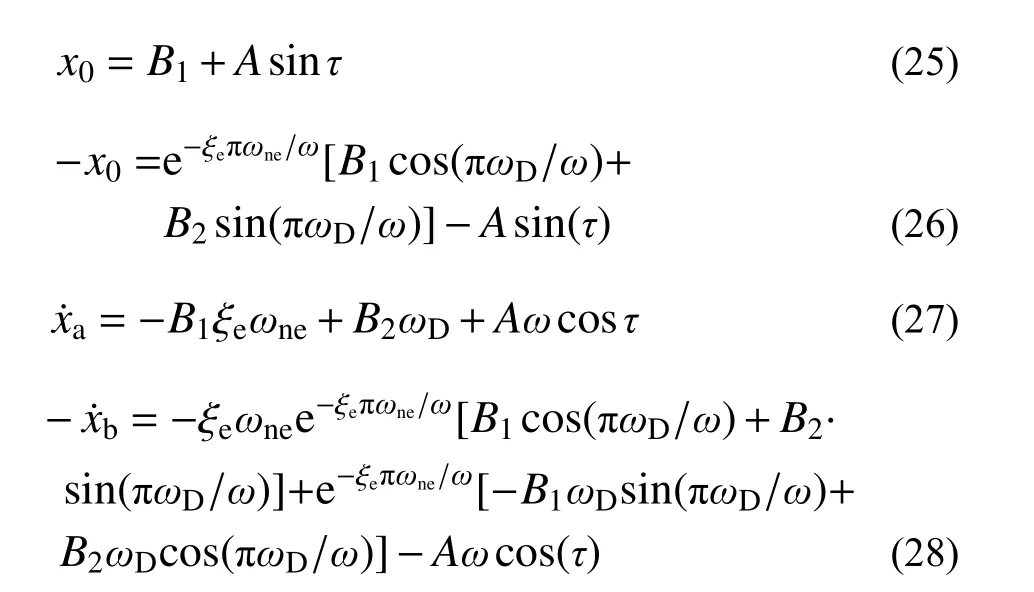
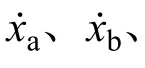
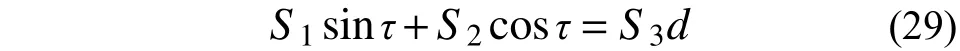
式中，S1、S2、S3为常数，由式(29)解得：

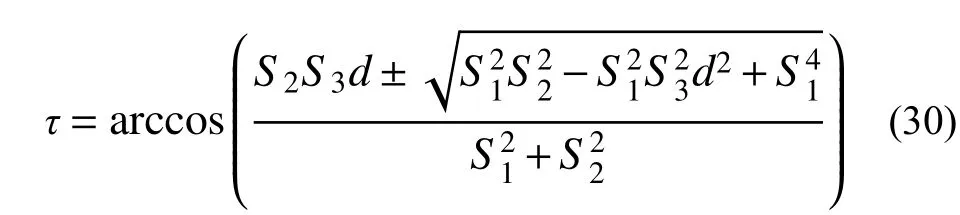
方程存在解的条件为：

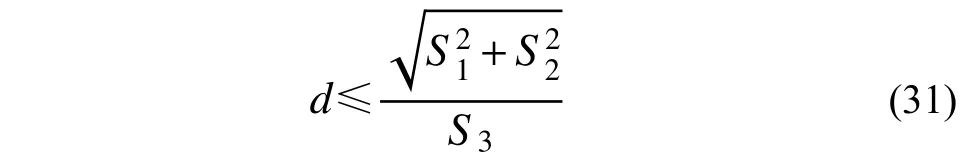
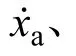
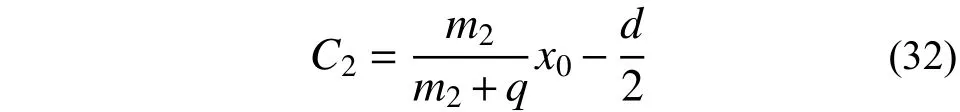
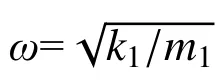
3.4 稳态解存在的碰撞间距d 取值范围讨论

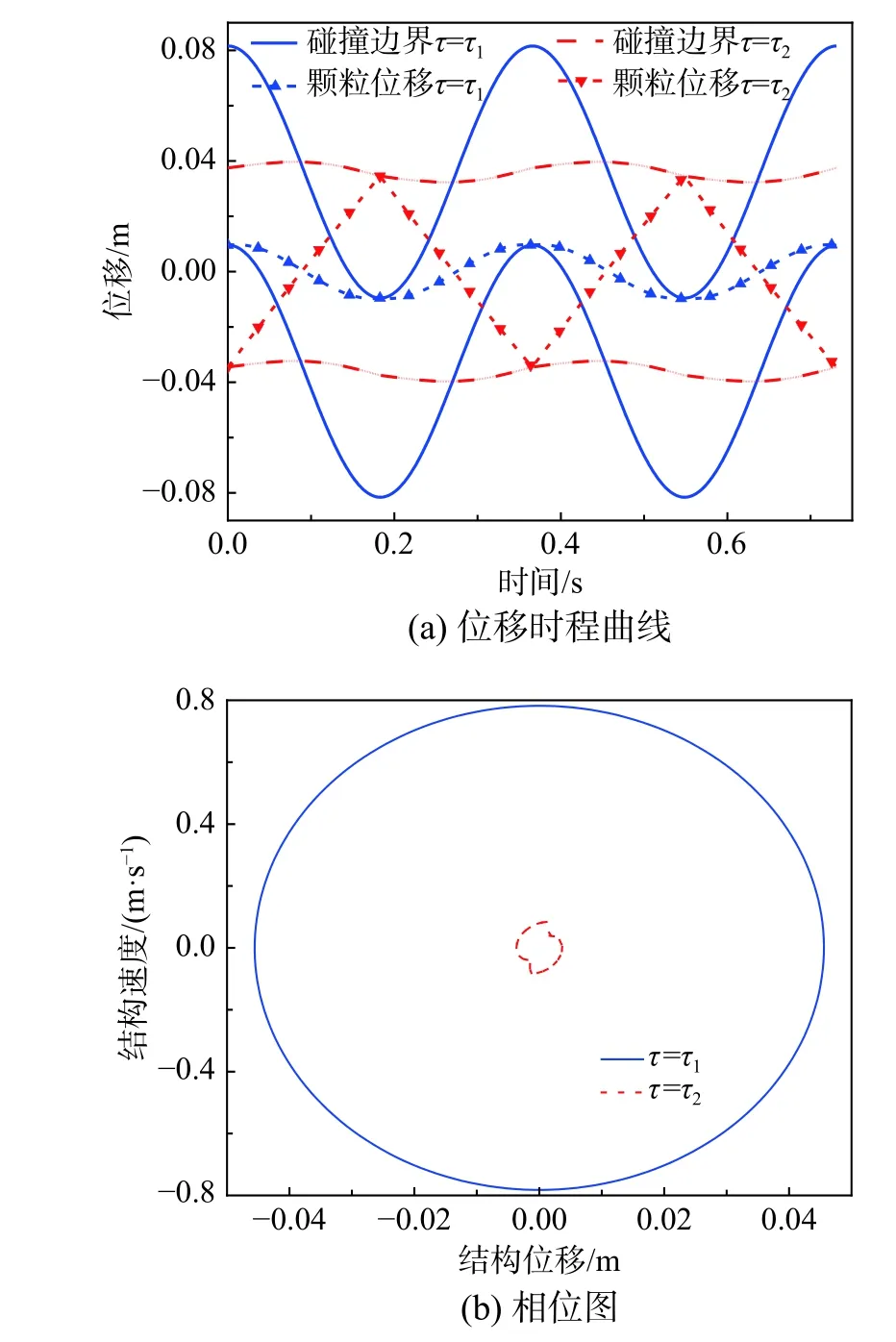
图 6 MPD-SDOF 运动状态Fig.6 Motion state of MPD-SDOF

式(31)给出了碰撞间距取值上限值的理论解。周期运动稳态解在推导过程中通过运动周期的端点运动状态即t=0、t=π/ω 状态最终求解单次碰撞稳态解析解，但是当碰撞间距较小时，颗粒在(0, π/ω)时间段内可能与结构发生碰撞，这也就限制了碰撞间距取值的最小值。在相邻两次碰撞之间，阻尼颗粒与结构之间的间距应满足：

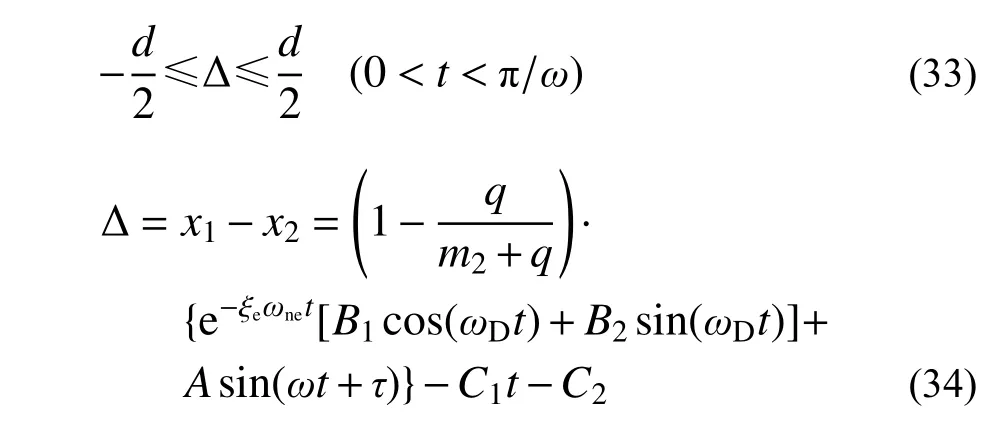
式中，B1、B2、C1、C2皆为碰撞间距d 的参数，由于式(34)的极值点较难求得理论解，本文基于二分法求得对应最小碰撞间距，其他参数与3.3 节的相关参数取值相同，图7 给出了碰撞区间d 随惯容系数q、频率比ω/ωn及碰撞恢复系数e 的变化曲线。图中dmax为式(31)所对应的最大碰撞间距；dmin为稳态解析解存在的最小碰撞间距取值。

由图7 可知：

1)碰撞恢复系数e 越小，颗粒群与结构发生碰撞时耗能越大。碰撞后的颗粒能量较小会导致颗粒群无法在较大的碰撞间距d 取值下仍然保持周期运动，因此随着碰撞恢复系数e 的减小，周期运动碰撞间距dmax取值逐渐变小。除此之外，当激励频率ω 远离结构自身频率ωn时，碰撞恢复系数对dmax影响较大；相比之下，当ω/ωn=1 时，dmax受碰撞恢复系数e 影响较小。这主要是由于结构自身运动受ω/ωn影响导致的(图4(a))。当ω 远离结构自身频率ωn时，此时结构位移较小，dmax取值较小，但是当e 较大时，仍然可以在较大的碰撞间距取值下保持周期运动；当ω/ωn=1 时，此时结构自身位移较大，因此即使e 较小也可以在较大的碰撞间距取值下保持周期运动。

2)惯质比λ 对周期运动碰撞间距取值影响分析表明，当ω 远离结构自身频率ωn时，由于λ 不利于颗粒与结构之间的相对运动(图4(b))，随着λ 的增加，dmax逐渐减小。当ω/ωn=1 时，此时dmax取值受λ 影响出现交叉现象。这是由于λ 的增加不仅减小了颗粒与容器之间的相对运动，也降低了结构自身运动幅值(图4(a))。在上述双重因素影响下，当e 较小时，λ 越大导致dmax越小；相反当e 较大时，λ 越大导致dmax越大。

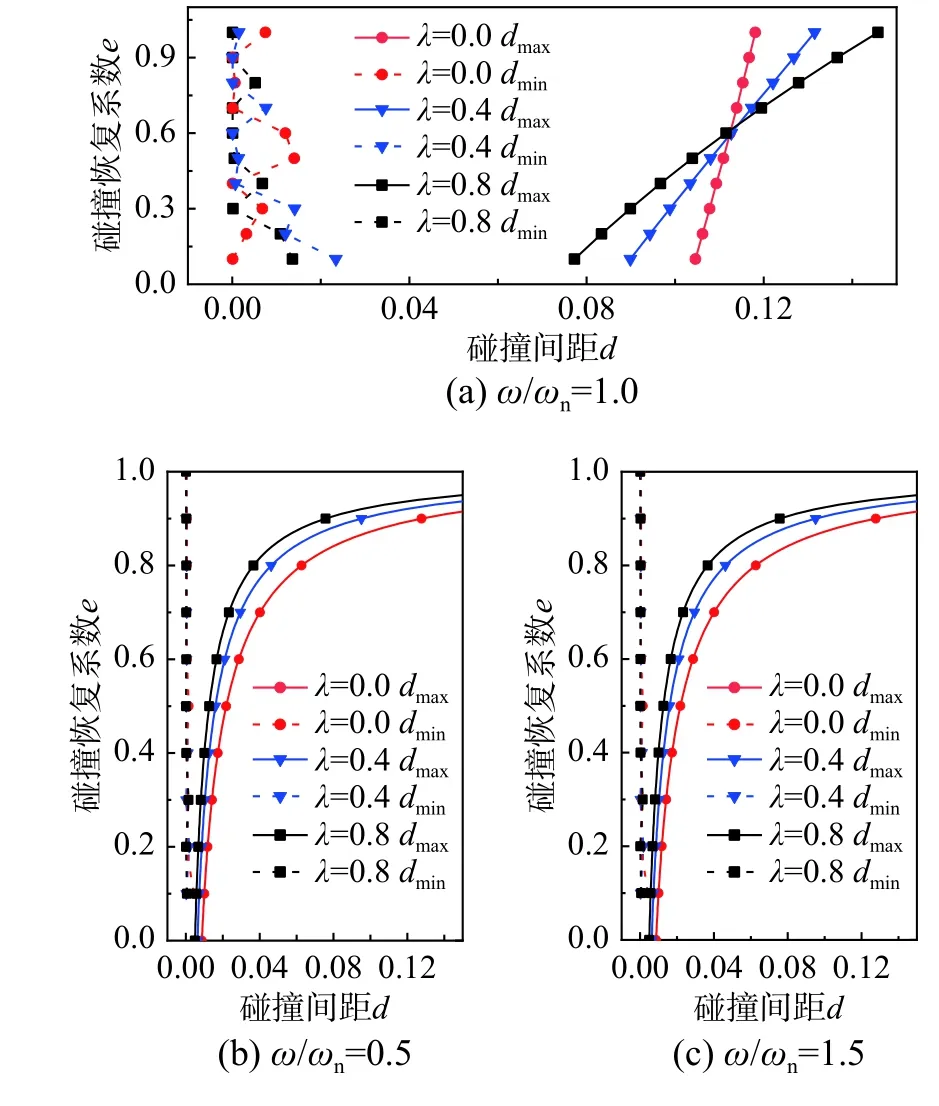
图 7 周期运动碰撞间距取值区间探讨Fig.7 Value interval of d for periodic motion

3.5 解析解的稳定性讨论

对于非光滑动力系统而言，周期运动解的稳定性分析对于进一步认识周期运动特性具有重要意义。文献[16]在求解单颗粒碰撞周期运动稳态解析解的基础上，通过求解误差传递矩阵P 讨论了周期解的稳定性。对于一个2 自由度体系，假设体系运动微分方程为：

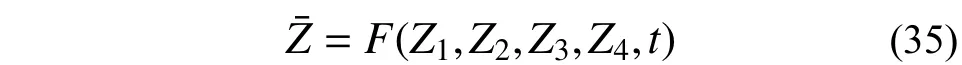
式中，Z1, Z2, Z3, Z4为必要的状态分量，运动微分方程一个特解可表示为：

假设该特解受到外部扰动而存在一定的误差，则考虑误差项后为：

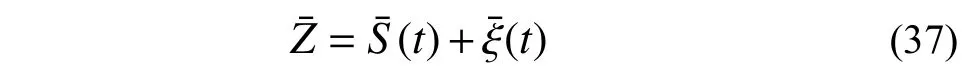
对应周期解渐进稳定的充分必要条件为：

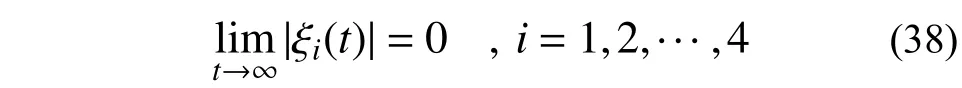
假设在结构体系周期运动的某次碰撞后引入误差，则对应n 次碰撞后误差项可以表示为：

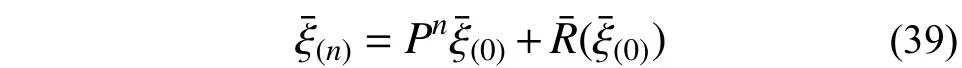
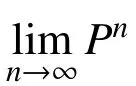
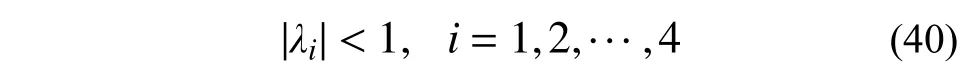
3.5.1 考虑惯容的MPD-SDOF 周期解的误差传递矩阵P 理论推导

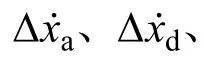
表 1 扰动前后状态对比Table 1 State comparison before and after disturbance

已知当颗粒不与结构发生碰撞时，结构体系位移如式(10)所示，对应体系速度为：

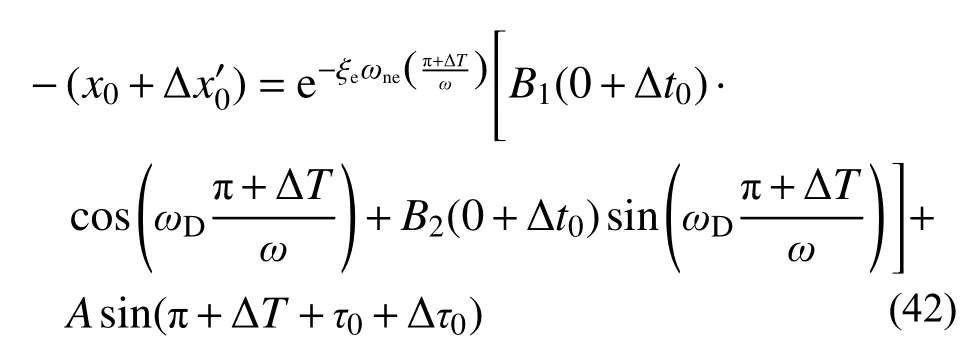
其中：

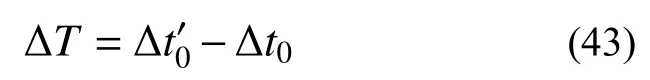
B1(0+Δt0)及B2(0+Δt0)一阶近似值如下所示：

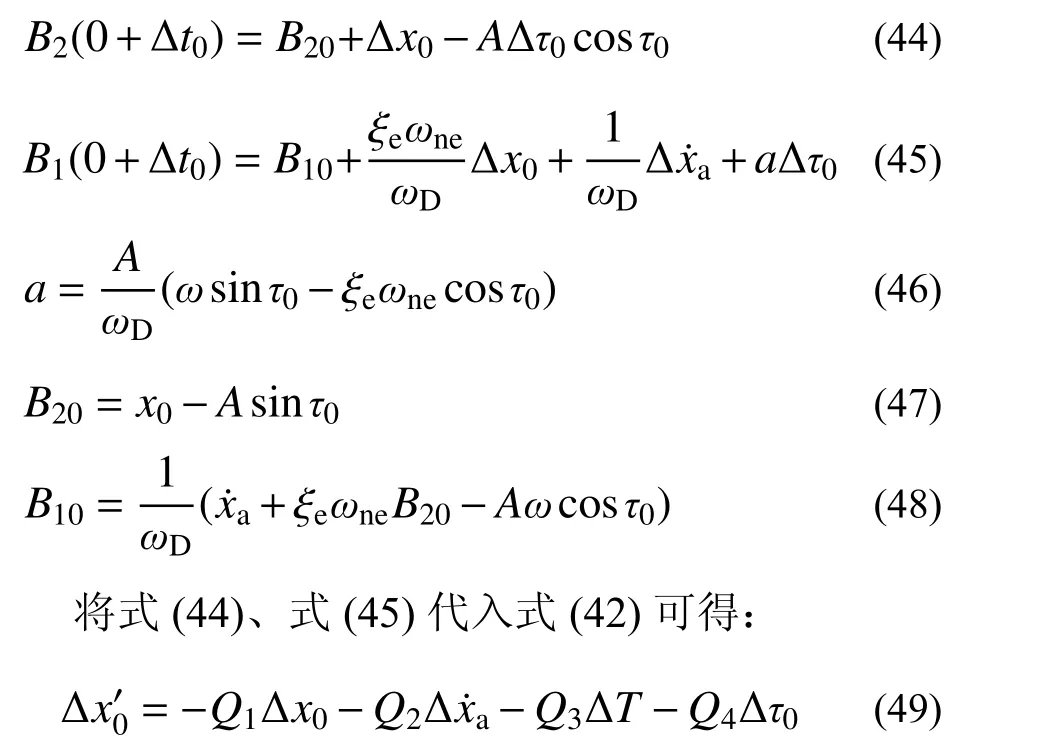
其中：

误差传递矩阵P 是与体系自身参数及周期运动碰撞边界条件相关的矩阵，当误差传递矩阵P 的特征值的模满足式(40)时，对应稳态周期碰撞运动稳定。

3.5.2 稳态周期碰撞运动稳定性理论推导数值验证

选取3.3 节对应MPD-SDOF 体系作为研究对象，以对应对称周期2 次碰撞条件作为初始条件，并基于MATLAB 自带ode45 算法以验证周期运动某次碰撞后扰动对体系运动稳定性的影响。模拟过程中当颗粒不与结构发生碰撞时，体系运动方程参考式(9)；当颗粒与结构发生碰撞时，认为碰撞瞬时完成，参考式(11)。由于算法自身误差缺陷，周期解稳定性分析过程中不再引入误差量。将体系参数及周期运动碰撞边界条件分别代入式(82)并求解P 的特征值，理论公式计算结果表明，当τ=τ1时，对应周期运动不稳定；当τ=τ2时稳定。对应碰撞后[0，20π/ω]时间段内的MATLAB数值模拟如图8 所示。

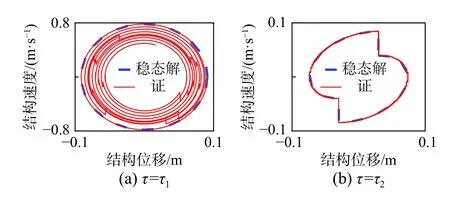
图 8 周期运动数值模拟Fig.8 Numerical simulation

由图像可知，当τ=τ1时，由于算法自身缺陷，周期运动并不稳定；当τ=τ2时，即使存在扰动，周期运动也较为稳定。本文采用的稳定分析方法具有实际参考价值。

3.5.3 惯容系数q 对周期运动稳定性分析

为进一步分析惯容系数q(q=λm2)对周期运动稳定区间的影响，选取3.3 节对应MPD-SDOF 体系作为研究对象，进行正交参数分析，基于式(82)分析惯容系数对周期解稳定区间的影响如图9 所示，图中虚线对应图7 碰撞间距取值区间。

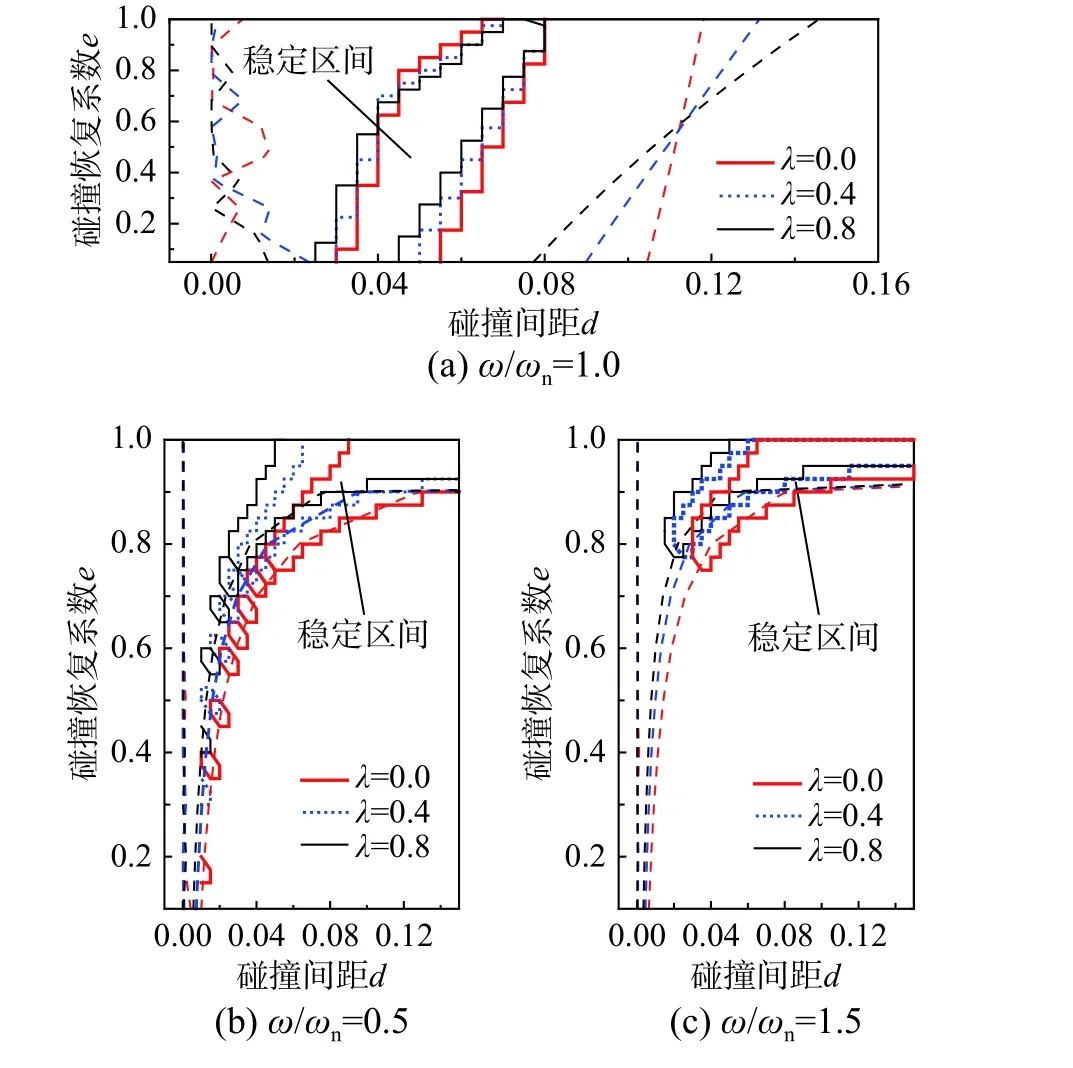
图 9 周期运动稳定区间Fig.9 Value interval of d for stable periodic motion

由图9 可知，不同激励下，周期运动稳定区间明显小于周期解存在的区间，且稳定区间不一定连续。稳定区间与周期解存在的最大碰撞间距dmax变化规律相近。随着e 的增加，周期运动稳定区间逐渐右移。当激励频率ω 远离结构自身频率ωn时，随着λ 的增加稳定区间向左偏移；当ω/ωn=1 时，随着λ 的增加稳定区间斜率逐渐增加。需要注意的是，当ω/ωn=1 时，随着e 的增加(e>0.7)，碰撞间距取值区间反而有所降低。这可能是由于共振频率激励下，结构位移及颗粒相对位移较大，此时e 越大，体系自身所具有的能量越大，对应周期运动越不宜稳定。同时，求解过程提示仅存在单个初始相位角τ 使系统的周期运动稳定，且该相位角对应结构运动最大位移较小的体系。这表明运动过程中结构体系易从能量较高的状态转变为能量较低的状态。相比之下，结构体系能量较低的周期运动稳定性更好。

4 理论解析试验验证

4.1 试验设计

为进一步验证基于考虑惯容影响的等效单颗粒力学模型进行的非碰撞阶段理论分析及周期运动解析的合理性，设计进行了简谐激励下单层钢框架电磁振动台试验。试验布置如图10 所示。其中试验模型的顶部钢板尺寸为500 mm×500 mm×5 mm；4 根框架柱高为500 mm，横截面尺寸为30 mm×5 mm；阻尼器腔体垂直于结构振动方向宽为300 mm，沿振动长度方向设置滑道控制两侧碰撞板之间的距离从而控制颗粒填充率。沿振动方向的最大长度为370 mm。通过电磁振动台台面及结构顶层布置的激光位移传感器分别拾取结构位移及实际振动台输入，并对应布置3 个加速度传感器拾取加速度响应。其中钢框架的质量为17.96 kg，刚度为5400 N/m，结构附加阻尼比为1.3%。试验简谐激励幅值取0.02 g，选择8 mm 钢珠作为阻尼颗粒，附加质量比为6%。通过调整两侧碰撞板间距依次进行30%、80%、90%、100%填充率在不同激振频率作用下的简谐激励振动台试验，其中填充率γ 取颗粒有序正方形排列投影面积与容器底面积之比。

图 10 试验模型Fig.10 Test model

4.2 未碰撞时理论解析试验验证

为初步验证考虑颗粒群惯容属性的合理性及重要性，首先进行未碰撞时理论解析试验验证。调整碰撞板间距进行填充率γ=30%时的振动台试验研究(当γ=30%时，颗粒群整体几乎不与结构发生碰撞，此时认为结构体系处于未碰撞阶段)，拾取结构及振动台台面位移响应计算均方根位移RMS 及位移均方根放大系数β 作为评价多颗粒阻尼器减振效果指标，位移均方根及放大系数计算如下：

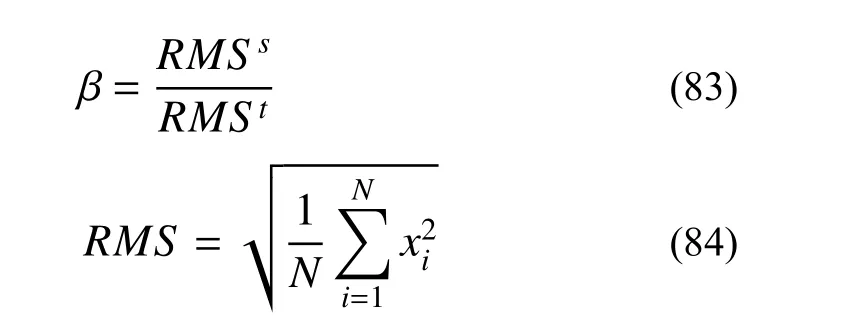
式中：xi为第i 个时间步的位移响应；N 为时间步数；上标s 和t 分别代表结构和振动台台面的位移响应。通过对比实测均方根位移放大系数频响曲线及位移放大系数频响曲线(式(6))确定多颗粒阻尼器惯质比λ。对比曲线如图11 所示。其中λ=0对应不考虑颗粒滚动对应拟合结果；λ=0.4 对应考虑颗粒滚动，但不考虑颗粒之间相互作用对应模型拟合结果；λ=0.8 对应基于试验结果拟合得到的考虑颗粒之间相互作用对惯容影响的理论结果。

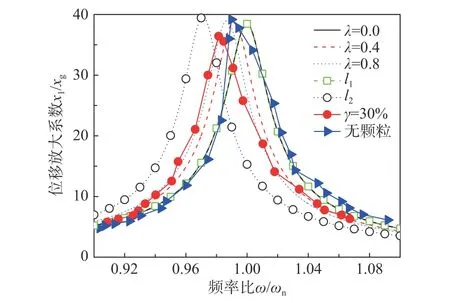
图 11 未碰撞时等效模型试验验证Fig.11 Test verification in non colliding stage

由图11 可知，当考虑颗粒之间相互作用对惯容系数q 的影响后(λ=0.8)，频响曲线总体拟合结果最为理想，对应相关系数R2=0.96。本文提出的考虑惯容后的等效单颗粒模型能够在一定程度上反应多颗粒阻尼器复杂非线性特性，对应理论解析是合理的。实测频响曲线、λ=0.8 及λ=0.4 对应频响曲线详细对比显示，对于多颗粒阻尼器，颗粒群在运动过程中的惯容属性与结构运动幅值存在一定的非线性关系。当x1/xg<15 时，实测频响曲线偏向λ=0.8 曲线右侧；而当x1/xg>15 时, 实测频响曲线偏向λ=0.8 曲线左侧。这可能是由于当结构运动幅值较小时，颗粒之间相互作用较弱，此时颗粒运动相互独立；而当结构运动幅值较大时，颗粒之间相互作用增加，颗粒之间的及颗粒与结构之间的相互作用增加了颗粒群的惯容属性，颗粒在运动过程中可能处于多维度运动状态。

4.3 周期2 次碰撞稳态解析试验验证

为进一步验证考虑惯容属性后周期2 次碰撞稳态解析的合理性，设计进行80%、90%及100%填充率下简谐激励振动台试验，其中等效模型参数取值参见文献[7，21]，颗粒群对应碰撞恢复系数e 为0.25；80%、90%及100%填充率下碰撞间距d 分别取20.7 mm、13 mm 及6.9 mm。不考虑填充率对惯容系数的影响，取λ=0.8，并综合考虑周期解的稳定性，取理论解析中结构最大位移较小的相位角作为对应理论周期运动。考虑周期稳定运动的存在性，本文仅陈列部分结果，如图12 所示。

由图12 可知，周期运动发生后，试验及模拟对应振动周期一致(T=2π/ω)，因此位移时程曲线除峰值外吻合较好。当γ=80%，ω/ωn=1.02 时，λ=0.8 对应均方根误差为18.05%；λ=0 对应均方根位移误差为60.24%。当γ=90%，ω/ωn=0.96 时，λ=0.8 对应均方根误差为14.4%；λ=0 对应均方根位移误差为23.23%。当γ=100%，ω/ωn=1.02 时，λ=0.8 对应均方根误差为29.22%；λ=0 对应均方根位移误差为44.94%。实测与理论解析对比分析结果显示，考虑惯容属性后拟合结果更加理想。本文得到的周期两次对称碰撞稳态解析解是合理的。需要注意的是，当γ=100%时，由于颗粒排布较为密集，运动过程中颗粒之间的碰撞耗能小于低填充状态下的耗能，等效模型中物理参数取值随填充率的增加存在一定的非线性关系，因此λ=0.8 对应的周期运动解析结果的精度并不理想。多颗粒阻尼器物理参数等效原则还有待进一步研究。

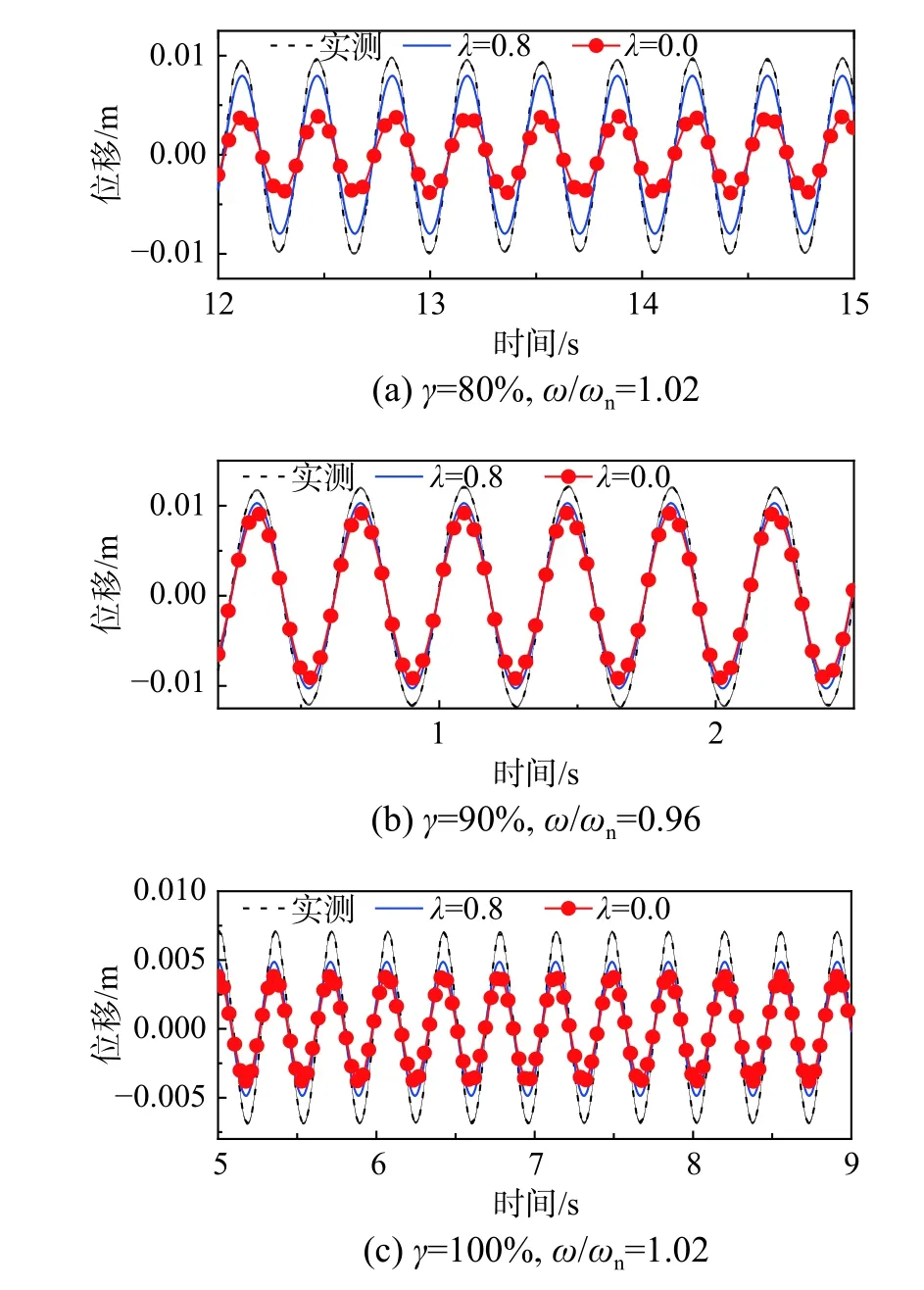
图 12 碰撞阶段试验验证Fig.12 Test verification in collision stage

考虑惯容与否对解析结果影响分析可知，当γ=80%，ω/ωn=1.02 时，λ=0.8 与λ=0 对应拟合结果误差差别较大，这是由于模型自身力学属性造成的。当λ=0 时认为颗粒在相邻两次碰撞之间做匀速运动。当γ=80%时，对应碰撞间距d 较大，此时颗粒与结构之间发生碰撞时的能量耗散及动量交换较为充分，对应结构位移较小。而当λ=0.8时，由于惯容的影响，颗粒在相邻两次碰撞之间的动能减小，颗粒的惯容作用不利于颗粒与结构之间的碰撞耗散及动量交换，对应结构位移较大。除此之外，由式(9)分析可知，惯容属性增加了主体结构的等效质量，因此结构位移更大。以上两个影响因素综合导致80%填充率下模型误差较大，且λ=0 对应结构位移响应小于λ=0.8 对应结构位移响应。当γ= 90%，ω/ωn=0.96 时，相比较与80%填充率，模型之间误差有所降低。这是由于惯容系数主要影响颗粒群非碰撞阶段，而90%填充对应碰撞间距较小，因此拟合结果较为接近。当γ= 100%，ω/ωn=1.02 时，同样因为碰撞间距较小，考虑惯容与否对拟合精度存在一定的影响但不明显。但总体而言，在不同填充率下都存在λ=0.8 对应结构位移高于λ=0 对应结构位移的现象。

此外，本文通过求解周期解析解分析了颗粒运动状态，但周期解的存在是有条件的，并非所有频率比下均存在周期解。另外由于实际简谐激励输入并不稳定，这往往导致振动体系较难稳定，实测数据与理论存在一定误差。综合80%、90%及100%填充率下不同频率比对应拟合结果显示，考虑颗粒群惯容属性后拟合结果更好。本文基于考虑惯容属性的等效单颗粒力学模型进行的理论解析是合理的。

5 结论

本文通过引入惯容器建立了具有惯容属性的多颗粒阻尼器等效单颗粒力学模型。结合阻尼颗粒的运动状态，依次进行了未碰撞时及发生碰撞后MPD-SDOF 系统的响应分析。主要结论如下：

(1) 当颗粒未发生堆积时，为考虑颗粒群滚动对多颗粒阻尼器减振效果的影响，本文引入了惯容器并建立对应等效单颗粒力学模型。理论分析及试验研究结果表明，颗粒群的惯容属性对颗粒阻尼器减振效果影响显著。考虑惯容后能够进一步考虑多颗粒阻尼器复杂的非线性特性，对应理论解析结果更加理想。

(3) 数值算例和试验结果表明，本文推导求解的多颗粒阻尼器对称2 次碰撞周期运动稳态解析解及其周期运动的稳定性分析是有效的。惯容系数(颗粒滚动)对颗粒阻尼器周期运动及稳定性具有一定的影响。当激励频率ω 远离结构频率ωn时，惯质比λ 越大，周期运动存在的碰撞区间大小逐渐减小，且稳定周期运动区间对应碰撞间距取值逐渐减小；当ω/ωn=1 时，随着λ 的增加dmax受碰撞恢复系数e 增加的影响逐渐增加。

本文进行的理论解析为颗粒阻尼器参数影响分析及减振机理研究提供理论支撑，可为颗粒阻尼器减震分析及设计所借鉴。需要指出的是受限于设备参数，本文并未考虑激励幅值对颗粒惯容属性的影响，相关研究将在后续成果中体现。