单轴对称十字型钢混凝土中长柱偏压性能试验研究

周天华，余吉鹏，张 钰，李亚鹏

(长安大学建筑工程学院，西安 710061)

实际工程中，型钢混凝土柱为满足不同的受力状态和建筑立面要求，需要灵活配置柱中型钢。建筑设计中，常采用“相连梁柱一侧同平面”的节点构造，导致梁柱中心线存在偏心距。为满足型钢混凝土梁偏心，组合柱中型钢非对称配置[1]，常见的非对称配钢形式，见图1。其中，图1(a)、图1(b)和图1(c)配钢形式分别适用于型钢混凝土边柱、角柱和中柱。

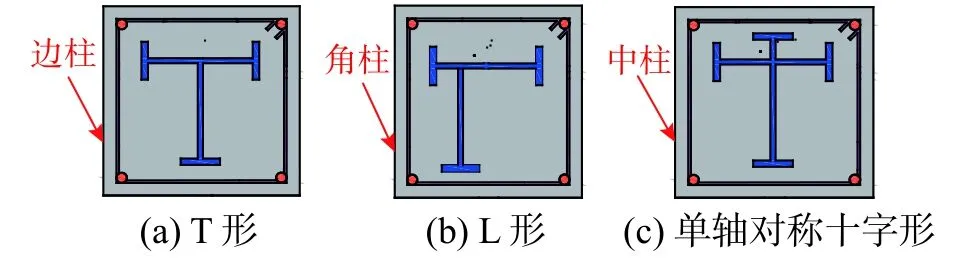
图 1 非对称型钢混凝土柱Fig.1 Steel reinforced column with unsymmetrical steel section

国内外学者对非对称型钢混凝土柱受力性能进行了研究，王秋维和史庆轩[2]对T 形型钢混凝土柱受力性能进行理论研究，提出该组合柱压弯承载力计算方法。曲哲等[3]根据非对称型钢混凝土柱受力特点，基于叠加原理，提出一种非对称型钢混凝土柱压弯承载力计算方法。Roik 和Bergmann[4]参考EC4，提出一种配置非对称型钢组合柱正截面承载力计算方法。曾磊等[5-6]对T 形和L 形型钢混凝土柱滞回性能进行研究，结果表明，型钢的非对称配置导致骨架曲线非对称。Chen 等[7]对T 形型钢混凝土构件滞回性能进行研究，结果表明，型钢的非对称配置对构件的滞回性能影响显著。Nishimura等[8]研究了轴压比和水平荷载作用方向对T 形型钢混凝土柱抗弯性能的影响，结果表明，水平荷载作用方向对试件抗弯性能影响较大。总而言之，配置T 形和L 形型钢对组合柱受力性能影响显著，因此，现有对称型钢混凝土柱的研究成果无法为该类组合柱的工程应用提供技术支持[9-11]，同时，目前关于非对称型钢混凝土柱的研究，缺乏对图1(c)所示单轴对称十字型钢混凝土柱受力性能的研究。

现行《组合结构设计规范》(JGJ 138-2016)[12]未给出单轴对称十字型钢混凝土柱正截面受压承载力计算方法，《钢骨混凝土结构设计规程》(YB 9082-2006)[13]第6.3.4 条规定：对于配置非对称钢骨截面的柱，当钢骨的非对称性不是很大时，可偏于安全地换算成对称截面，这样导致计算的承载力偏于保守，材料利用率较低，故有必要对该组合柱偏压性能及其正截面受压承载力计算方法进行研究。

本文设计了8 个单轴对称十字型钢混凝土中长柱试件，对其偏心受压性能进行研究，分别分析不同加载方向十字型钢偏心率和荷载偏心率对该组合柱偏压性能的影响，采用极限平衡法，以平截面假定为基础，建立既能保持现有规范形式，又能考虑十字型钢偏心的组合柱正截面受压承载力计算方法，为该组合柱的工程应用提供参考。

1 试验概况

1.1 试件设计

试验设计了8 个单轴对称十字型钢混凝土中长柱试件，试件长宽高为350 mm×250 mm×3000 mm，试件长细比l0/h=9.4≥8，其中，l0为试件计算长度，h 为柱截面高度，则本文试件为中长柱[14]。试件按《组合结构设计规范》(JGJ 138-2016)[12]进行设计，其中，纵筋采用4 20，箍筋采用10@100，柱端牛腿箍筋加密为 10@50mm。型钢腹板和翼缘分别采用8 mm 和10 mm 的Q235B钢板焊接，含钢率为6.4%。牛腿处焊接两块8 mm厚加劲板，防止牛腿局部破坏，试件截面尺寸及构造见图2。试验参数为十字型钢偏心率(ea/h)和荷载偏心率(e0/h)，试件参数设置见表1，其中，ea为十字型钢偏心距[15]，e0为荷载偏心距，规定荷载偏心方向和十字型钢偏心方向相同时，荷载偏心距e0为正，否则为负值。

1.2 材性试验

试件混凝土强度等级为C40，混凝土立方体试块(150 mm×150 mm×150 mm)抗压强度为44.8 MPa，钢材材性试验结果见表2。

图 2 截面尺寸及配筋 /mm Fig.2 Cross-section and reinforcement details

表 1 主要参数与试验结果Table 1 Parameters of specimens and experimental results

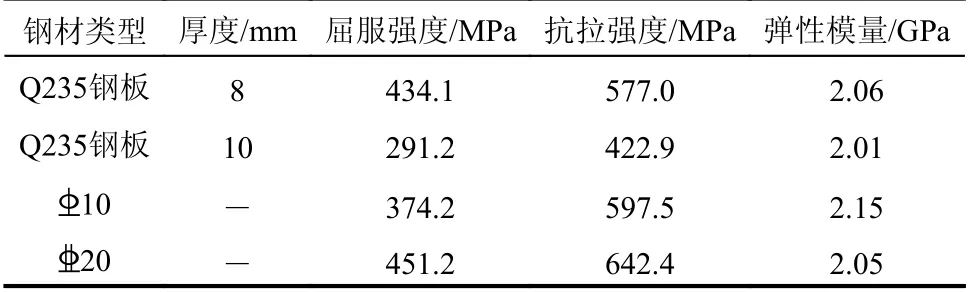
表 2 钢材材料性能Table 2 Material properties of steel

1.3 组合柱截面特征

对于单轴对称十字型钢混凝土柱，其荷载偏心距以该组合柱截面物理形心轴为基准[4,16]，因此，要确定不同试件截面物理形心轴。

如图3 所示，其中，Oa为纵向H 型钢截面对称轴，Oc为组合柱截面几何形心轴，Om为组合柱截面物理形心轴[13,15]，Oa轴偏离Oc轴的距离为十字型钢偏心距ea[15]，采用强度换算法确定物理形心om位置，则om到y 轴距离xm为[4]：

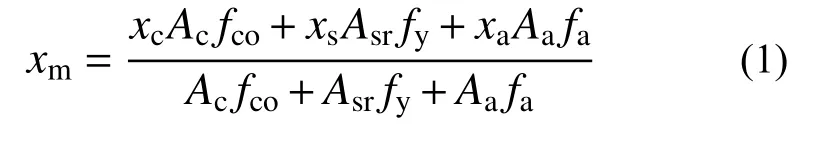
式中：Asr为纵筋面积；fa和fy分别为型钢和纵筋屈服强度，其余参数定义见文献[15]。由式(1)计算的不同试件xm，结果见表1。

图 3 试件截面特征Fig.3 Sectional feature of specimens

1.4 加载测试方案

试验在长安大学结构工程实验室5000 kN 长柱压力试验机上进行，见图4(a)。试验加载前，在试件两端各设置一块20 mm 钢板，同时在柱两端牛腿采用钢夹具进行加固，避免牛腿局部受压破坏。试件两端设置刀铰，则柱边界条件为两端铰支，以组合柱截面物理形心轴为基准，确定不同试件荷载偏心距。正式加载时，采用位移控制加载，加载速率为0.15 mm/min，直到试件破坏[17]。

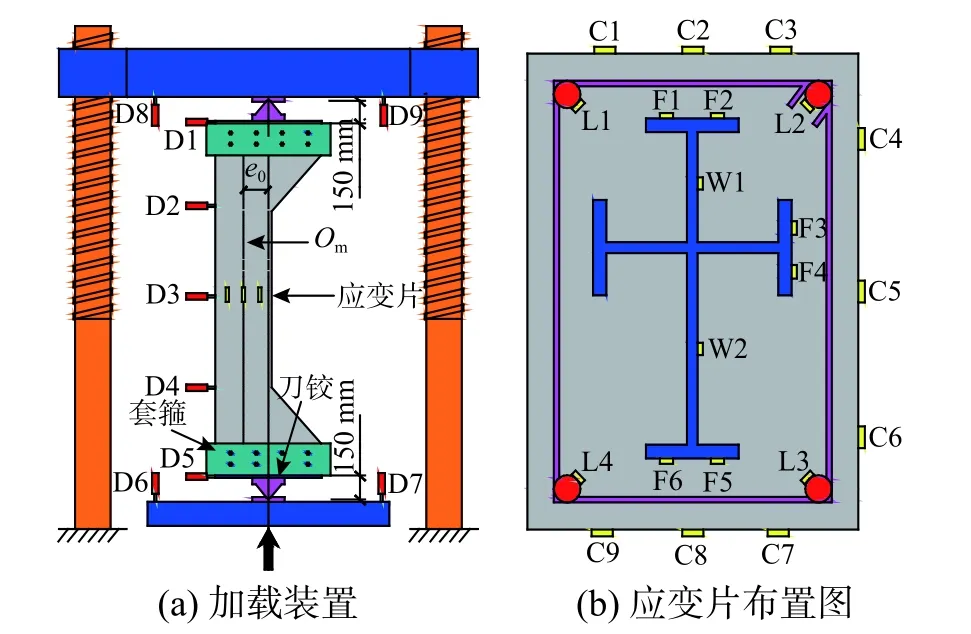
图 4 加载装置及测点布置Fig.4 Test setup and measuring point arrangement

为测量试件变形情况，采用图4(a)所示位移计布置方式，沿试件高度方向布置5 个位移计D1～D5，测量试件侧向挠度，在试验机加载端和固定端各布置2 个位移计D6～D9，测量试件轴向变形。

按图4(b)布置应变片，测量试件中间截面混凝土、纵筋、型钢应变变化情况，其中，应变片C1～C9 测量试件中间截面混凝土应变，应变片L1～L4 测量纵筋应变发展情况，应变片F1～F6 测量型钢翼缘应变变化情况，应变片W1～W2 测量型钢腹板应变。

2 试验结果及分析

2.1 试验现象

在偏心受压荷载作用下，试件均发生强度破坏，试件破坏形态与对称十字型钢混凝土柱类似[18]。在两个偏心方向上，十字型钢偏心率对试件破坏形态影响相对较小，荷载偏心率对试件破坏形态影响较大，根据荷载偏心率的不同，试件分成小偏心受压破坏和大偏心受压破坏两种形态。

1) 小偏心受压破坏

对于荷载偏心率e0/h=0.2 和e0/h=-0.2 的试件(SRC-1-1、SRC-1-3、SRC-2-1 和SRC-2-3)，试件表现出小偏心受压破坏特征。以试件SRC-1-1 为例，描述试件破坏过程：加载前期，试件处于弹性阶段，试件表面无明显现象。当荷载达到0.4Nm(Nm为峰值荷载)左右时，试件中部受拉区出现首条水平裂缝，荷载增加，不断有新的裂缝出现，但裂缝发展缓慢。当荷载达到0.85Nm左右时，试件中部受压区出现纵向裂缝，荷载不断增加，受压区混凝土不断开裂，纵向裂缝不断向柱两端延伸，伴随着混凝土压溃声，侧向挠度增长速率加快。当荷载达到0.95Nm左右时，试件受压区角部混凝土开始剥落，荷载继续增加，突然发出“嘭”一声，受压区混凝土突然崩开，试件达到峰值荷载。继续加载，荷载下降速率较快，受压区混凝土大面积剥落，侧向挠度不断增大。纵筋压曲，试件破坏，试件混凝土最终受压区压溃高度约为80 cm，试件破坏形态见图5(a)。

2) 大偏心受压破坏

对于荷载偏心率e0/h=1.0 和e0/h=-1.0 的试件(SRC-1-2、SRC-1-4、SRC-2-2 和SRC-2-4)，试件表现出大偏心受压破坏特征。以试件SRC-1-2 为例，介绍试件破坏过程：当荷载增加到0.15Nm左右时，试件受拉区出现首条水平裂缝，荷载增加，试件中部受拉区不断出现新的水平裂缝。当荷载增加到0.6Nm左右时，受拉区水平裂缝宽度不断增加，试件中部形成数条主裂缝，荷载继续增加，受拉区牛腿根部也相继出现水平裂缝，试件的侧向挠度增长速率加大。当荷载达到0.9Nm左右时，试件受压区表面出现纵向裂缝，继续加载，纵向裂缝向柱两端延伸，受压区混凝土表面出现起皮脱落，此时受拉区主裂缝宽度较大，试件侧面裂缝逐渐向受压区延伸，侧向挠度继续增大。当荷载增加到0.95Nm左右时，受压区角部混凝土剥落，伴随混凝土压溃声，试件达到峰值荷载。继续加载，受压区混凝土大面积剥落，荷载缓慢下降，侧向挠度不断增大，纵筋压曲，箍筋外露，试件破坏，受压区混凝土压溃高度约为45 cm，试件破坏形态见图5(b)。

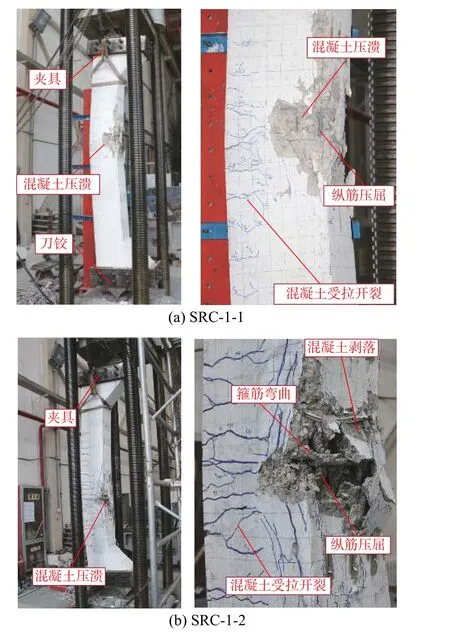
图 5 试件破坏形态Fig.5 Failure patterns of specimens

根据上述试验结果可知，小偏心受压破坏和大偏心受压破坏过程均可分成：未裂阶段、带裂缝工作阶段和破坏阶段。荷载偏心率不同，试件带裂缝工作阶段时间不同，荷载偏心率e0/h=0.2 和e0/h=-0.2 的试件，从开裂到破坏时间相对较短，试件破坏预兆不明显，试件受压区压溃区面积较大(图6(a))；荷载偏心率e0/h=1.0 和e0/h=-1.0 的试件，带裂缝工作阶段时间较长，试件破坏前，受拉区水平裂缝发展充分，试件破坏预兆明显，受压区混凝土压溃面积较小(图6(b))。两种破坏模式最终破坏形态为受压区边缘混凝土压溃，而型钢内混凝土基本保持完好，原因是型钢对混凝土有一定的约束作用。试验过程中，未见试件表面出现明显的粘结滑移裂缝，说明型钢与混凝土能够较好地协同工作。

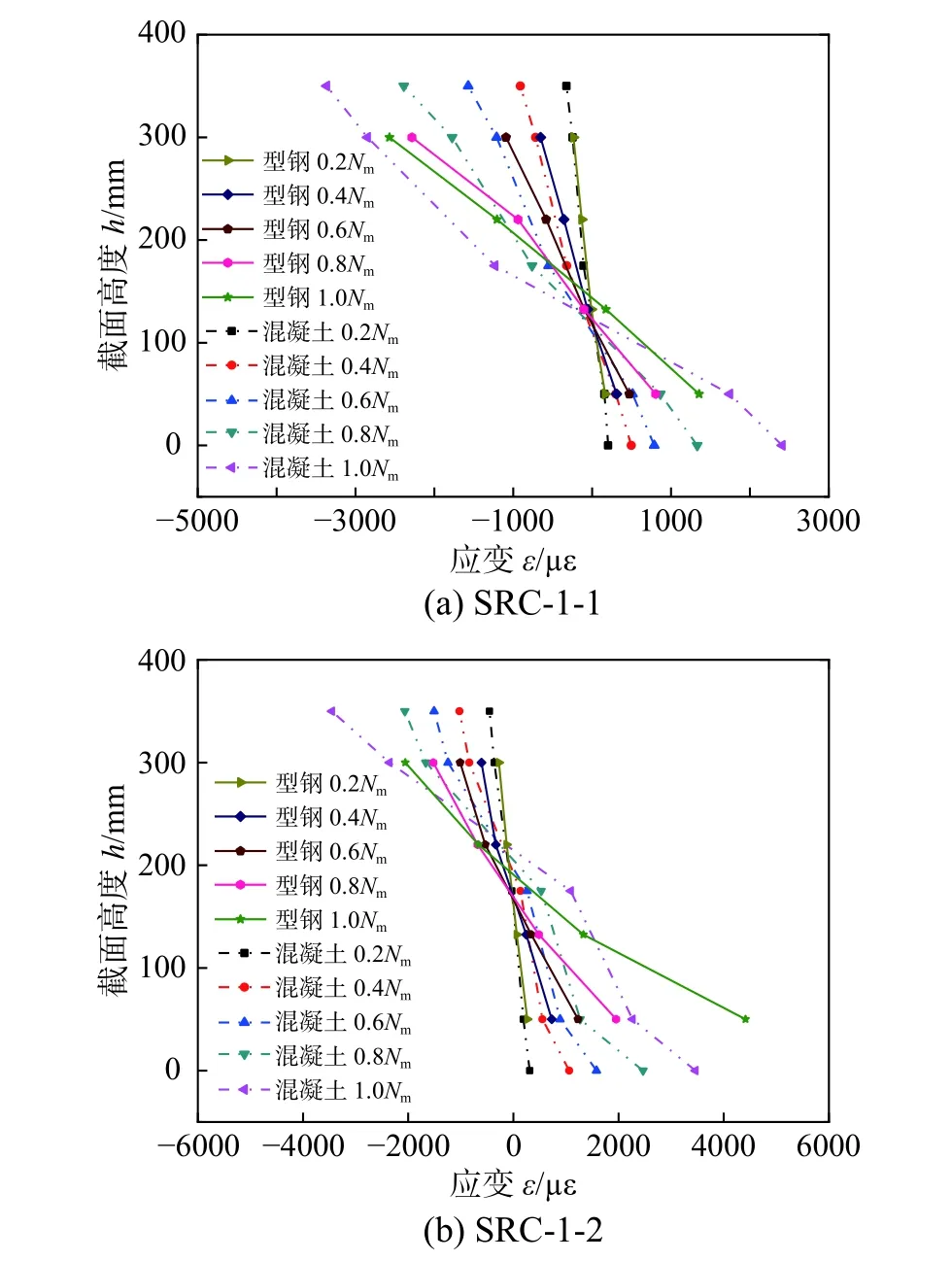
图 7 典型试件荷载-应变曲线Fig.7 Load-strain curves of typical specimens

图 6 试件裂缝分布Fig.6 Distribution of cracks of specimens

2.2 截面应变分布

不同荷载水平下，试件SRC-1-1 和SRC-1-2混凝土和型钢应变分布曲线见图7。

由图7(a)可知，对于试件SRC-1-1，荷载达到Nm时，受压区边缘混凝土压溃，其极限压应变为3364 με，受压区型钢翼缘压应变为2569 με，受压翼缘达到屈服，受拉区型钢翼缘拉应变为1356 με，受拉区型钢翼缘未达到屈服，说明试件SRC-1-1 截面应变发展规律符合小偏心受压破坏特征[18]。

由图7(b)可知，对于试件SRC-1-2，当荷载增加到0.8Nm时，受拉翼缘应变为1954 με，翼缘受拉屈服，而受压区边缘混凝土压应变为2464 με。当荷载达到Nm时，受压区边缘混凝土应变为3450 με，达到其极限压应变，表明试件受压区边缘混凝土达到极限压应变前，受拉区型钢翼缘已经屈服，说明试件SRC-1-2 截面应变发展规律符合大偏心受压破坏特征[18]。

由图7 可知，荷载偏心率增加，试件跨中截面受压区高度减小；虽然两试件破坏模式不同，但两试件达到峰值荷载时，受压区边缘混凝土都被压溃，达到其极限压应变；峰值荷载前，试件混凝土和型钢应变发展规律基本一致，截面应变呈直线分布，说明型钢和混凝土变形协调，符合平截面假定。

2.3 侧向挠度

不同荷载水平下试件侧向挠度曲线见图8，由图8 可知，加载初期，试件侧向挠度增长速率较慢，当荷载增加到0.8Nm，侧向挠度增长速率加快，加载过程中，试件跨中挠度始终最大，因此，在试件极限承载力计算时，试件跨中截面为控制截面。加载过程中，试件侧向挠度对称分布，基本满足正弦半波曲线。对于正向和负向偏心，十字型钢偏心率对试件侧向挠度影响相对较小，荷载偏心率对试件侧向挠度影响较大，随着荷载偏心率增大，试件侧向挠度显著增大。

2.4 影响因素分析

试件不同加载方向的荷载-跨中挠度曲线见图9，试件峰值荷载Nm及峰值挠度Δm见表1。

轴向荷载作用下，单轴对称十字型钢混凝土柱混凝土产生横向变形，型钢对混凝土产生约束作用，提高混凝土强度和变形能力，改善组合柱受力性能。对于本文不同十字型钢偏心率和荷载偏心率的组合柱试件，型钢对混凝土的约束作用不同，影响组合柱偏压受力性能。

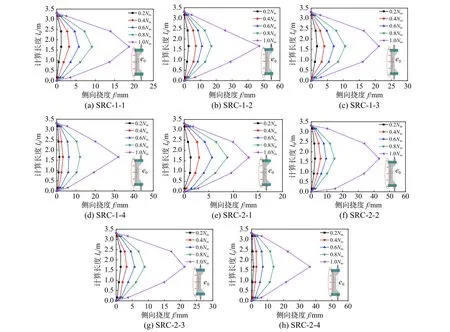
图 8 侧向挠度曲线Fig.8 Lateral deflection curves

为便于参数分析，图10 给出了轴压荷载作用下，单轴对称十字型钢混凝土柱截面约束区的划分，根据箍筋和型钢约束作用的不同，组合柱截面可分成非约束区、部分约束区、型钢弱约束区和型钢强约束区[19]。其中，非约束区混凝土不受约束作用，部分约束区混凝土受箍筋双向约束作用，型钢弱约束区混凝土受箍筋双向和型钢单向约束作用，型钢强约束区混凝土受箍筋和型钢的双向约束作用[15]。

2.4.1 十字型钢偏心率的影响

由图9 和表1 可知：

1) 对于正向偏心，当荷载偏心率(e0/h)为0.2时，试件发生小偏心受压破坏，十字型钢偏心率从0.1 增加到0.2，试件极限承载力和峰值挠度分别下降了2.7%和11.2%；当荷载偏心率(e0/h)为1.0，试件发生大偏心受压破坏，十字型钢偏心率从0.1 增加到0.2，试件极限承载力和峰值挠度分别下降了2.8%和8.0%，原因是十字型钢偏心率越大，纵向H 型钢离试件受压较大边越近(图10)，其变形越大，承担更多的轴向荷载；对于正向偏心，型钢强约束区混凝土受压应力较大，型钢约束作用对组合柱偏压性能影响较为显著，十字型钢偏心率越大，型钢对混凝土约束作用越不均匀，型钢约束效率越低[15,20]，混凝土强度提高的幅度越小，对该组合柱偏压承载力产生不利影响，故总体上，组合柱极限承载力和变形能力随十字型钢偏心率增大而小幅降低。

2) 对于负向偏心，当荷载偏心率(e0/h)为-0.2时，试件发生小偏心受压破坏，十字型钢偏心率从0.1 增加到0.2，试件极限承载力和峰值挠度分别上升了1.0%和1.4%，说明十字型钢偏心率对小偏心受压破坏的试件偏压性能影响较小，原因是单轴对称十字型钢对混凝土的约束应力主要集中在型钢翼缘和腹板、腹板和腹板相交处[15,21]，与正向偏心相反，在负向偏心荷载作用下，型钢强约束区混凝土受压应力较小，混凝土变形小，型钢对其约束作用没有充分发挥，故型钢对混凝土约束作用对组合柱偏压承载力影响较小；同时，发生小偏心受压破坏的试件，纵向H 型钢受拉或受压，但其变形较小，承担的荷载也较小，增大十字型钢偏心率，对试件偏压承载力影响不明显，故十字型钢偏心率对小偏心受压破坏试件承载力影响较小。

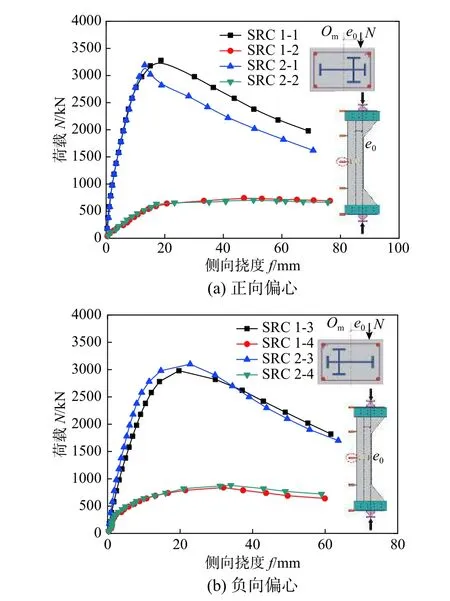
图 9 荷载-侧向挠度曲线Fig.9 Load-lateral deflection curves

图 10 组合柱截面区域划分Fig.10 Regional partition for composite column

3)对于负向偏心，当荷载偏心率(e0/h)为-1.0时，试件发生大偏心受压破坏，十字型钢偏心率从0.1 增加到0.2，试件极限承载力和峰值挠度分别上升了4.8%和7.3%，这是因为对于负向偏心，型钢强约束区混凝土受拉(图10)，型钢对混凝土的约束作用难以发挥，故型钢对混凝土约束作用对组合柱偏压承载力影响较小；而试件发生大偏心受压破坏时，受拉翼缘应变较大，达到峰值荷载时，受拉翼缘已经屈服，十字型钢偏心率越大，纵向H 型钢离受拉翼缘越近，其受拉作用能够得到发挥，故对于负向大偏心受压破坏的试件，其极限承载力和变形能力随十字型钢偏心率增大而提高。

2.4.2 荷载偏心率的影响

由图9 和表1 可知，无论是正向偏心，还是负向偏心，增加荷载偏心率，试件荷载-跨中挠度曲线的初始刚度及极限承载力均大幅下降，但试件达到峰值荷载后，荷载下降缓慢，后期变形能力较好，以正向偏心试件为例，当十字型钢偏心率(ea/h)为0.1 时，荷载偏心率从0.2 增加到1.0，试件极限承载力下降了77.4%，峰值挠度上升了175.2%；十字型钢偏心率(ea/h)为0.2 时，荷载偏心率从0.2 增加到1.0，试件极限承载力下降了77.2%，峰值挠度上升了184.9%，说明荷载偏心率对试件偏压性能影响较大，试件极限承载力随荷载偏心率的增大而大幅减小，但试件变形能力显著上升。

3 正截面受压承载力计算

单轴对称十字型钢混凝土柱偏心受压破坏模式与普通型钢混凝土柱类似，参照《组合结构设计规范》(JGJ 138-2016)[12]，采用截面极限平衡理论，建立该组合柱正截面受压承载力计算方法。

3.1 基本假定

在进行单轴对称十字型钢混凝土柱正截面受压承载力计算时，基本假定为[9]：

1) 截面保持平面；

2) 忽略混凝土抗拉强度；

3) 混凝土极限压应变为0.003；

4) 型钢拉压梯形应力图简化为拉压矩形应力图。

3.2 单轴对称十字型钢混凝土柱正截面受压承载力计算方法

在建立单轴对称十字型钢混凝土柱正截面受压承载力计算方法时，为简化计算，将单轴对称十字型钢横向腹板按式(2)等效至两侧翼缘中，等效截面见图11。

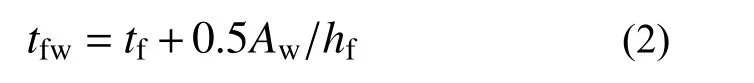
式中：tfw为等效后两侧等效翼缘厚度；Aw为横向腹板净面积；hf和tf分别为型钢两侧翼缘高度和厚度。

单轴对称十字型钢混凝土偏心受压柱等效截面计算参数示意见图12。

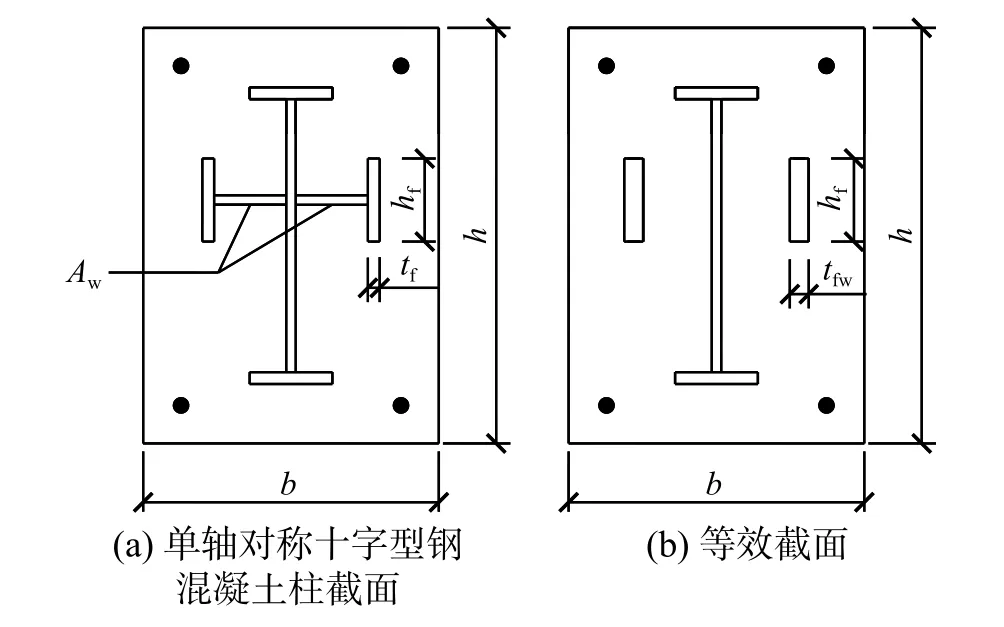
图 11 组合柱截面简化Fig.11 Simplification of cross-section of composite column

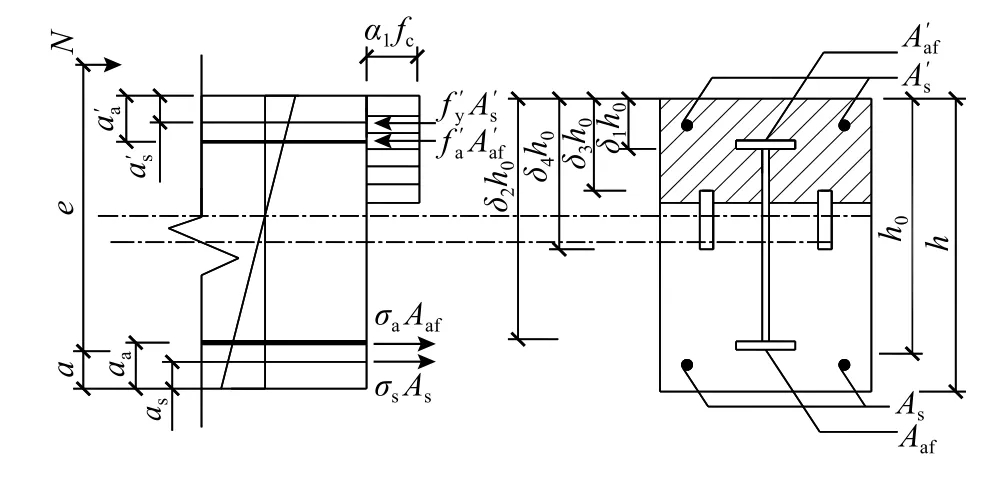
图 12 计算参数示意图Fig.12 Diagram of calculation parameters

由内力平衡得：

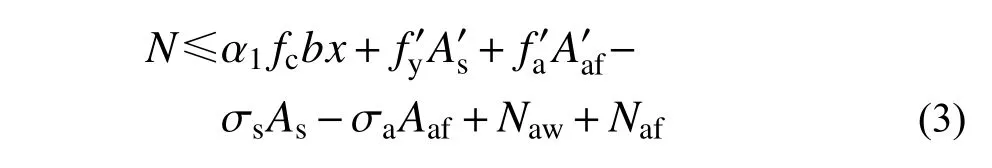
对受拉或受压较小边型钢翼缘和纵向钢筋合力点取矩，由力矩平衡得：

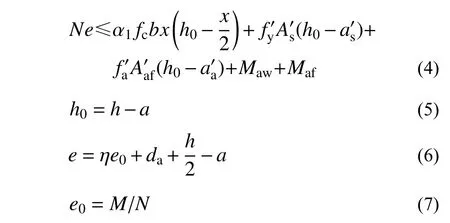
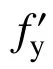
在建立单轴对称十字型钢混凝土柱正截面受压承载力计算方法中，关键是计算式(3)和式(4)中的Naw、Maw、Naf和Maf。

3.3 型钢腹板和两侧等效翼缘承担的Naw、Maw、Naf 和Maf 计算方法

在计算型钢腹板和两侧等效翼缘承担的Naw、Maw、Naf和Maf时，引入参数δ1、δ2、δ3和δ4来确定型钢腹板和两侧翼缘在截面中位置(图12)，δ1和δ3分别为型钢腹板和两侧翼缘上端至截面上边缘的距离与h0的比值，δ2和δ4分别为型钢腹板和两侧翼缘下端至截面上边缘的距离与h0的比值。本文将混凝土受压区应力图简化为矩形应力图，其高度按平截面假定确定的中和轴高度乘以受压区混凝土应力图影响系数β1，则应变中和轴高度为x/β1，本文β1取0.8[12]。计算Naw、Maw、Naf和Maf时，型钢腹板和两侧等效翼缘拉、压应力状态以中和轴为界限，根据中和轴在组合柱截面中的位置，建立Naw、Maw、Naf和Maf的计算方法。

3.3.1 当腹板处于拉、压应力状态，两侧等效翼缘处于拉应力状态

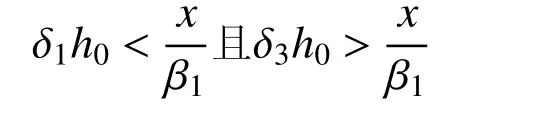
当腹板处于拉、压应力状态，两侧等效翼缘处于拉应力状态时，计算参数示意见图13。

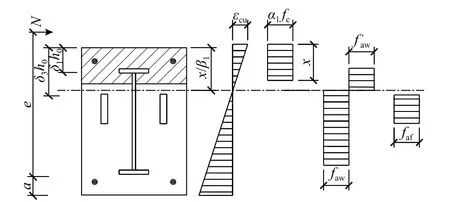
图 13 腹板和等效翼缘计算参数示意(情况1)Fig.13 Diagram of calculation parameters of steel web and equivalent flanges (case 1)

1) 两侧等效翼缘承受的总轴向合力Naf

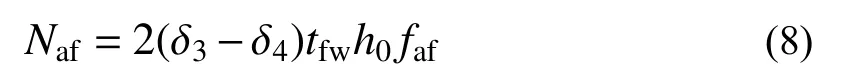
2) 两侧等效翼缘承受的总弯矩Maf

由于型钢腹板处于拉、压应力状态，则腹板承受的轴向合力和弯矩分别按JGJ 138-2016[12]第6.2.2 条式(6.2.2-9)和(6.2.2-10)计算。

3.3.2 当腹板和两侧等效翼缘处于拉、压应力状态

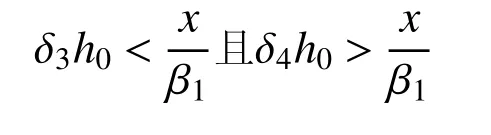
当腹板和两侧等效翼缘均处于拉、压应力状态时，计算参数示意见图14。

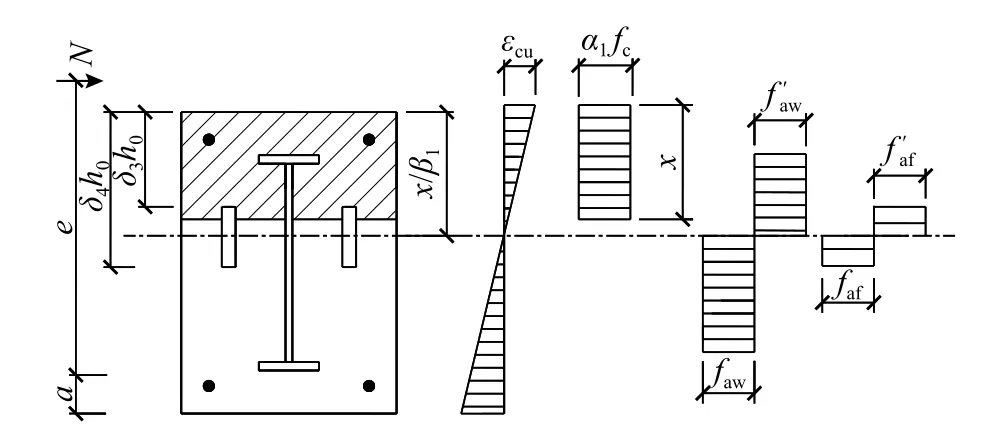
图 14 腹板和等效翼缘计算参数示意(情况2)Fig.14 Diagram of calculation parameters of steel web and equivalent flanges (case 2)

1) 两侧等效翼缘承受的总轴向合力Naf

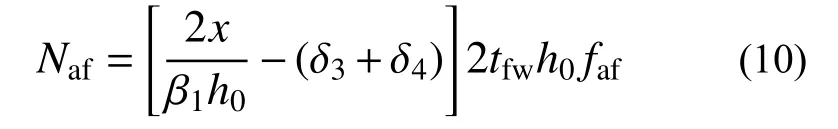
2) 两侧等效翼缘承受的总弯矩Maf

腹板承受的轴向合力和弯矩分别按JGJ 138-2016[12]第6.2.2 条式(6.2.2-9)和(6.2.2-10)计算。

3.3.3 当腹板处于拉、压应力状态，两侧等效翼缘处于压应力状态

当腹板处于拉、压应力状态，两侧等效翼缘处于压应力状态时，计算参数示意见图15。

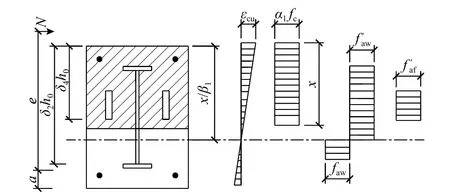
图 15 腹板和等效翼缘计算参数示意(情况3)Fig.15 Diagram of calculation parameters of steel web and equivalent flanges (case 3)

1) 两侧等效翼缘承受的总轴向合力Naf

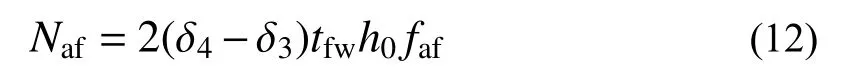
2) 两侧等效翼缘承受的总弯矩Maf

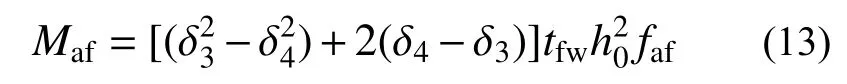
腹板承受的轴向合力和弯矩分别按JGJ 138-2016[12]第6.2.2 条式(6.2.2-9)和(6.2.2-10)计算。

3.3.4 当腹板和两侧等效翼缘均处于压应力状态

当腹板和两侧等效翼缘均处于压应力状态时，计算参数示意见图16。

图 16 腹板和等效翼缘计算参数示意(情况4)Fig.16 Diagram of calculation parameters of steel web and equivalent flanges (case 4)

由于型钢腹板和两侧等效翼缘均处于压应力状态，则腹板承受的轴向合力和弯矩分别按JGJ 138-2016[12]第6.2.2 条式(6.2.2-11)和式(6.2.2-12)计算，两侧等效翼缘承受的总轴向合力和总弯矩分别按式(12)和式(13)计算。

3.4 相对界限受压区高度ξb 计算

根据平截面假定，计算相对界限受压区高度ξb，图17 中钢材屈服应变εy取受拉钢筋和受拉翼缘的屈服应变平均值，则相对界限受压区高度ξb按JGJ 138-2016[12]第6.2.2 条式(6.2.2-15)计算。

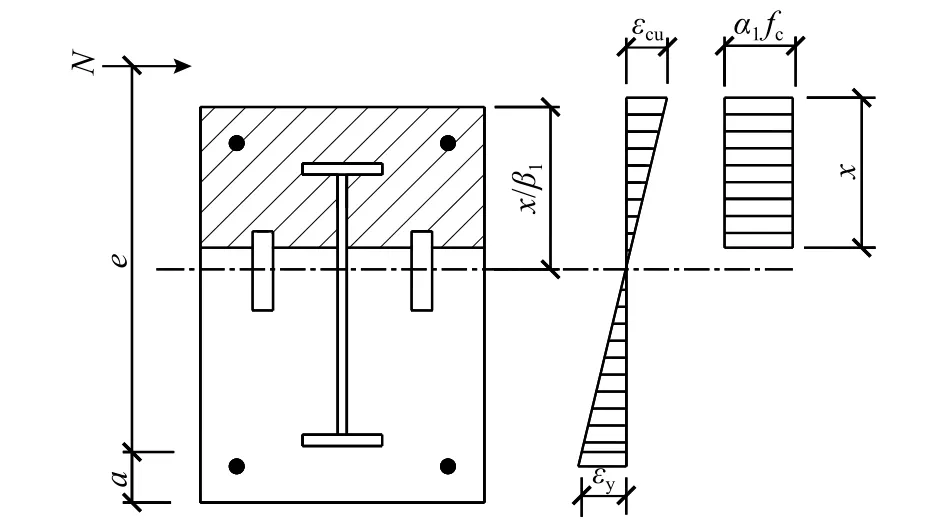
图 17 界限破坏柱截面应变示意Fig.17 Sectional strain diagram of boundary failure of column

3.5 公式验证

不考虑纵向H 型钢的作用，将单轴对称十字型钢偏于安全地换算成H 型钢，采用JGJ 138-2016[12]中型钢混凝土柱正截面受压承载力计算方法计算试件偏压承载力NJGJ，同时，采用本文提出的方法计算单轴对称十字型钢混凝土柱试件偏压承载力Nc，计算中材料强度均采用实测值，上述两种方法计算的试件N-M 相关曲线，见图18，试件偏压承载力计算结果见表3。

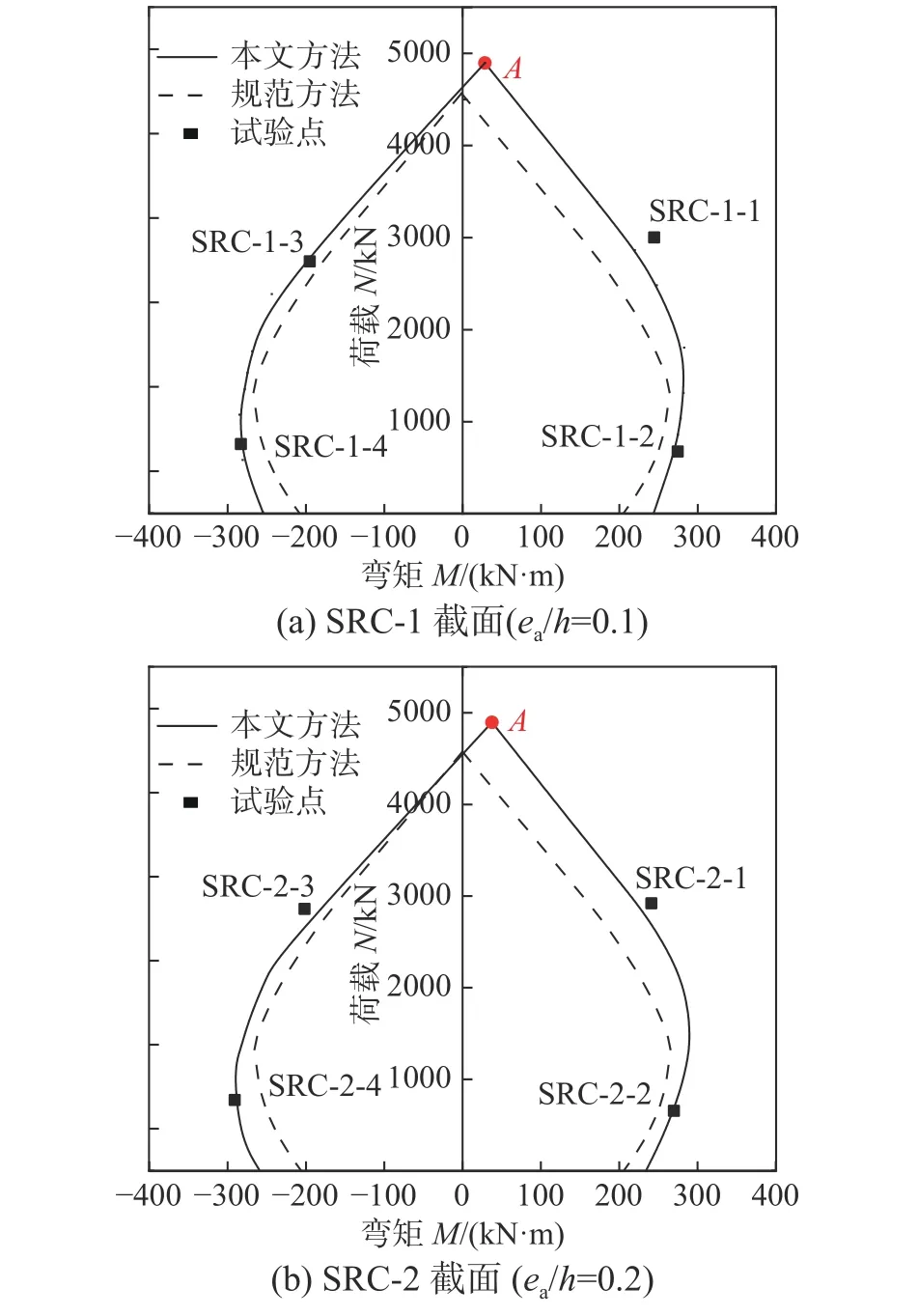
1000载2000 4000 5000A 1000载2000 4000 5000本文方法A试验点规范方法本文方法试验点规范方法荷 N/kN3000荷 N/kN3000 SRC-1-3SRC-1-1 SRC-1-2 SRC-1-4-400 -300 -200 -100 0 100 200 300 400弯矩 M/(kN·m)-400 -300 -200 -100 0 100 200 300 400弯矩 M/(kN·m)(a) SRC-1 截面(ea/h=0.1)SRC-2-3SRC-2-1 SRC-2-4SRC-2-2(b) SRC-2 截面 (ea/h=0.2)

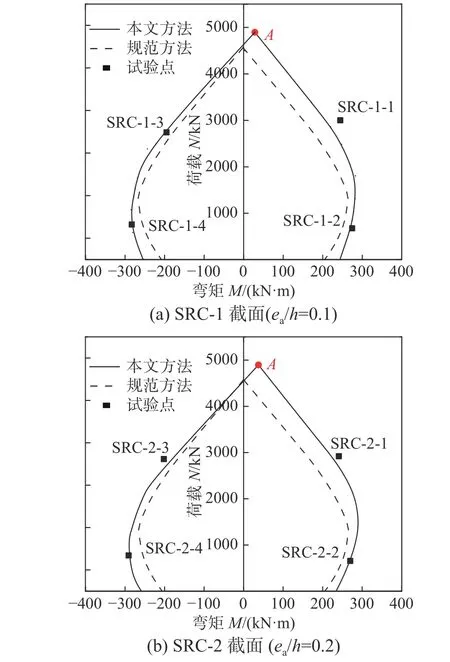
图 18 N-M 相关曲线Fig.18 N-M interaction curves

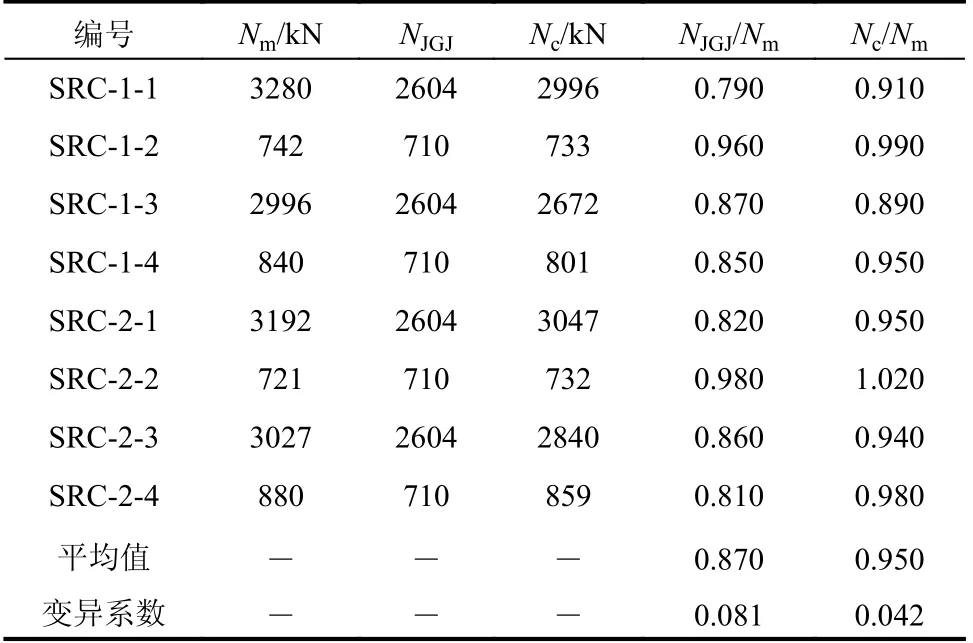
表 3 试验结果与计算结果比较Table 3 Comparison between test results and computed results

由 表3 可知，采用JGJ 138-2016 和本文计算方法得到的试件偏压承载力计算值与试验值比值的均值分别为0.87 和0.95，变异系数分别为0.081和0.042，同时，图18 中采用JGJ 138-2016 计算的试件N-M 相关曲线偏于保守，而采用本文计算方法得到的组合柱N-M 相关曲线与试验结果吻合较好，且偏于安全。值得注意的是，两种方法计算的试件N-M 相关曲线形状存在差异，本文方法计算的单轴对称十字型钢混凝土柱的N-M 相关曲线轴力最大点A 不在N 轴上，原因是单轴对称十字型钢混凝土柱截面物理形心轴Om与几何形心轴Oc不重合，轴向压力NA对几何形心轴Oc存在弯矩MA[13]，而规范计算方法无法考虑十字型钢偏心对该组合柱偏压承载力的影响。

本文提出的组合柱正截面受压承载力计算方法同样适用于十字型钢混凝土柱，为验证本文计算方法对十字型钢混凝土柱的适用性，对文献[22]中十字型钢混凝土柱抗弯承载力进行计算，结果见表4。

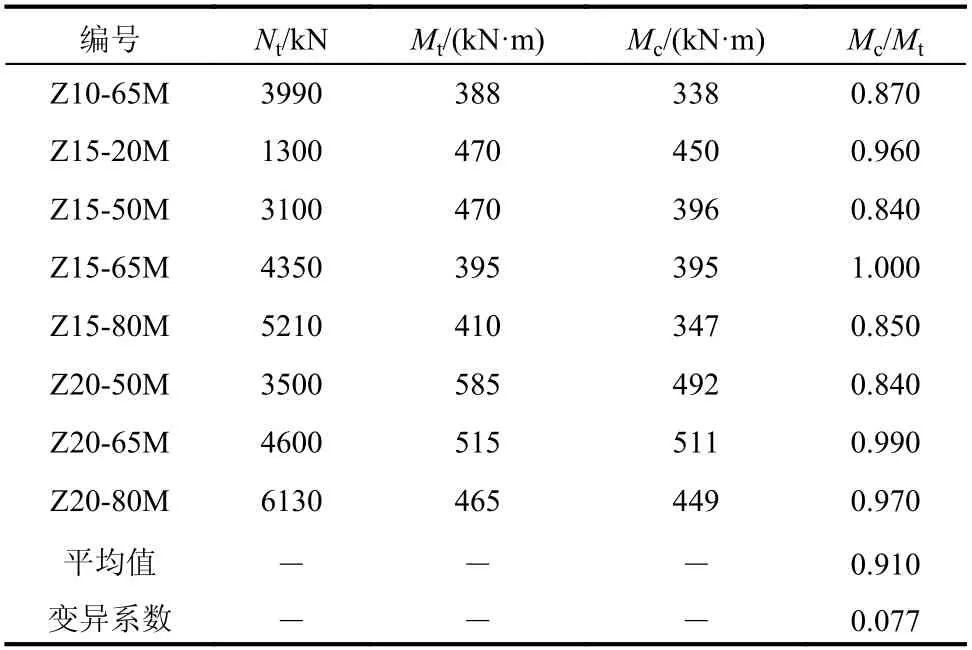
表 4 文献[22]试验结果与计算结果比较Table 4 Comparison between test results in literature [22] and computed results

由表4 可知，采用本文方法计算的试件抗弯承载力计算值与试验值比值的均值为0.91，变异系数为0.077，说明本文计算方法适用于十字型钢混凝土柱。结合本文试验及上述计算结果，从安全合理的角度，建议本文提出的单轴对称十字型钢混凝土柱正截面受压承载力计算公式十字型钢偏心率适用范围为：-0.25≤ea/h≤0.25。

4 结论

本文对8 个单轴对称十字型钢混凝土中长柱偏压性能进行了试验研究，分析了十字型钢偏心率和荷载偏心率对该组合柱偏压受力性能的影响规律，建立了该组合柱正截面受压承载力计算公式，得到以下结论：

(1) 对于单轴对称十字型钢混凝土中长柱试件，当荷载偏心率为0.2 和-0.2 时，试件发生小偏心受压破坏；荷载偏心率为1.0 和-1.0 时，试件发生大偏心受压破坏。组合柱截面应变基本保持直线，型钢和混凝土能够协同工作。试件侧向挠度曲线上下对称，呈正弦半波分布。

(2) 在本文参数变化范围内，正向偏心时，增大十字型钢偏心率，组合柱极限承载力和变形能力小幅度降低；负向偏心时，增大十字型钢偏心率，对小偏心受压破坏试件偏压性能影响较小，发生大偏心受压破坏的试件极限承载力和变形能力略有上升。荷载偏心率对试件初始刚度和极限承载力影响较大，荷载偏心率增大，试件极限承载力大幅降低，试件变形能力显著上升。

(3) 基于平截面假定，本文提出与规范形式一致，且考虑十字型钢偏心影响的单轴对称十字型钢混凝土柱正截面受压承载力计算方法。将单轴对称十字型钢偏于安全地换算成H 型钢，采用JGJ 138-2016 计算其偏压承载力，计算结果偏于保守，而本文提出的计算方法精度较高，建议本文提出的计算方法十字型钢偏心率适用范围为-0.25≤ea/h≤0.25。