改进滞变阻尼模型的时域计算方法

孙攀旭，杨 红,2

(1. 重庆大学土木工程学院，重庆 400045；2. 重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045)

合理的阻尼模型是结构动力响应计算结果正确的关键之一，黏性阻尼模型和复阻尼模型是最为常用的两种阻尼模型[1-3]。黏性阻尼模型具有数学简易性，计算过程简便[4-5]，但结构每周期耗散能量与外激励频率相关，这与大部分工程材料的试验结果不符[6]。复阻尼模型是在试验结果的基础上建立的，且具有每周期耗散能量与外激励频率无关的优点，但其自由振动通解中包含发散项，导致时域计算结果不能稳定收敛[7-9]。如何克服复阻尼模型的缺陷，成为亟待解决的问题。

关于复阻尼模型的时域发散问题，常见的解决途径是结合其他阻尼模型的优点，构造出等效复阻尼模型，以实现动力响应的时域计算。例如，采用复频率法[10-11]、应变能法[12-13]等计算出等效阻尼比，可得到等效黏性阻尼模型；Boit[14]提出了核函数为Voigt 函数的等效指数阻尼模型，为保证计算精度，可将核函数进一步拓展为Maxwell-Wiechert 函数[15-17]。廖振鹏[18]、周正华等[19]、Yang 等[20]为避免指数阻尼的复杂计算过程，采用最小二乘法得到一种等效于复阻尼模型的五参数黏弹性本构模型；Wang[21]将复阻尼矩阵等效为Rayleigh 阻尼矩阵，提出了等效Rayleigh阻尼模型，刘庆林等[22]在此基础上进一步提出了等效Caughey 阻尼模型。

上述等效复阻尼模型的主要问题是误差估计较为困难，且等效准则的合理性难以判定。因此，一些学者直接对修正复阻尼模型进行研究，期望解决其缺陷。朱镜清和朱敏[23]、Pan 等[24]直接舍弃自由振动通解中发散项的计算方法，保证了计算结果的稳定性，但这种处理在数学上不够精确[25-26]，并且也没有克服复阻尼模型本身存在的缺陷。Clough 和Penzien[1]、Chen 等[27]对复阻尼模型进行了修正，假定阻尼力的大小与结构体系的位移大小成正比，且与速度的方向相反，提出了迟滞阻尼模型，以保证结构每周期耗散能量与外激励频率无关，但存在耗能不守恒和非线性的问题。笔者[28]在迟滞阻尼模型的基础上，利用能量守恒得到了改进迟滞阻尼模型，但没有解决非线性的问题。朱镜清[29]和笔者[30]在复阻尼模型的基础上，构建出频率相关黏性阻尼模型，以处理时域发散问题，但未考虑正、负频率共轭的影响。Inaudi 和Kelly[31]引入正、负频率共轭的条件，对复阻尼模型的频域运动方程进行了修正，并提出了对应的滞变阻尼模型。滞变阻尼模型不仅保证了运动方程的完备性，且有效解决了复阻尼模型自由振动通解中的发散问题[32]，但滞变阻尼模型的有阻尼自振频率随着损耗因子的增加而增加，与实际不符。

在上述研究的基础上，本文在保留滞变阻尼模型每周期耗散能量与外激励频率无关的优点的情况下，通过构建改进滞变阻尼模型，在复数域内建立改进滞变阻尼模型的拉氏运动方程及相应的时域运动方程。然后依据信号识别方法，结合改进滞变阻尼模型的时域运动方程特点，提出基于傅里叶变换的时域计算方法和基于希尔伯特-黄变换的时域计算方法，以实现结构动力响应的时域计算。

1 改进滞变阻尼模型

1.1 复阻尼模型

在谐波作用下，大部分工程结构存在稳态反应每周期耗散能量与外激励频率无关的试验现象，依据试验现象可构建出复阻尼模型的频域运动方程[33]：

-ϖ2mY(iϖ)+iηkY(iϖ)+kY(iϖ)=-mP(iϖ) (1)

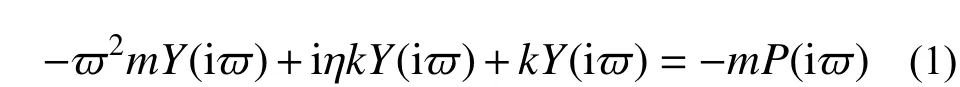
式中： m 为结构的质量； k 为结构的刚度； η为结构的损耗因子；P(iϖ) 为p(t)的傅里叶变换项；

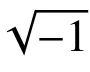
式中： A 为谐波的振幅； θ为谐波的振动频率。

式中：y(t)为结构位移响应的复数表达式；实部x(t)为结构的位移响应。

采用傅里叶逆变换，式(1)对应的时域运动方程为：

m¨y(t)+iηky(t)+ky(t)=-mp(t)(4)

式(4)是建立在谐波作用下结构的稳态反应基础上的，仅适用于分析谐波作用下结构的稳态反应。将式(4)进一步推广到外激励作用下包含结构瞬态反应和稳态反应的时域过程中，对应的运动方程为：

m¨y(t)+iηky(t)+ky(t)=-mg(t)(5)

式中，g(t)为外激励加速度。

文献[34]的研究结果表明式(5)不是完备方程，求解得到的结构动力响应明显偏小。为保证方程的完备性，利用复化对偶原则[25,35]对式(5)进行修正，可得对应的时域运动方程为：

m¨y(t)+iηky(t)+ky(t)=-m[g(t)+ig′(t)](6)

式中，g′(t) 为g(t)的复化对偶项。

式(6)对应的自由振动方程为：

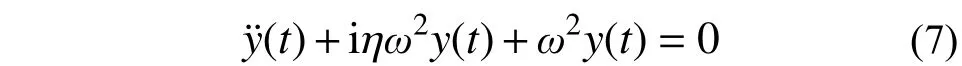
式(7)的自由振动响应表达式为：

式中， A1、 A2、 A3和 A4为待定系数，可由初始条件进行确定。

由式(8)和式(9)可知复阻尼模型的自由振动响应中包含指数增长项，其时域计算结果将会随着外部作用时间的增加，逐渐出现发散现象。

对式(6)进行傅里叶变换，得到对应的频域运动方程为：

式中：G(iϖ) 为g(t)的傅里叶变换项；G′(iϖ)为g′(t)的傅里叶变换项。

取式(10)中结构位移响应对应的频域运动方程，可得：

式中，X(iϖ) 为x(t)的傅里叶变换项。

1.2 滞变阻尼模型

为考虑负频率的影响，将式(11)进行改进，得到基于复阻尼模型的滞变阻尼模型频域运动方程为[31-32]：

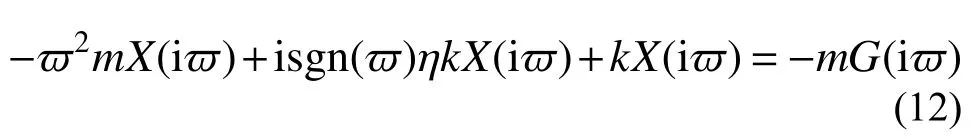
其中：

对式(12)进行傅里叶逆变换，可得到滞变阻尼模型的时域运动方程为：

式中，xH(t) 为x(t)的希尔伯特变换项。

式(14)对应的自由振动响应的表达式为：

式中， B1和 B2为待定系数，可由初始条件进行确定。

由式(15)和式(16)可知，滞变阻尼模型的自由振动响应中不包含发散项，保证了时域计算结果的稳定收敛。

复化对偶原则为：

希尔伯特变换原则为：

式中：[sin(θt)]H为sin(θt)的希尔伯特变换；[cos(θt)]H为cos(θt)的希尔伯特变换。

由式(17)和式(18)对比可知，复阻尼模型的复化对偶原则实质上就是希尔伯特变换。因此，滞变阻尼模型在保留了复阻尼模型的完备性基础上，克服了复阻尼模型的时域发散缺陷。但由式(16)可知，随着损耗因子的增加，有阻尼自振频率 ωh将逐渐增大。这种现象与实际不符。

1.3 改进滞变阻尼模型

式(12)在计算过程中采用的是复平面法，ϖ为复频率，对应的符号函数sgn(ϖ)与式(13)的定义是矛盾的，从而导致滞变阻尼模型的时域方程中有阻尼自振频率随着损耗因子的增加而增加。针对该问题，考虑到复频率的虚部为结构的振动频率，在频域内本文提出改进滞变阻尼模型，即将式(12)进一步改进为：

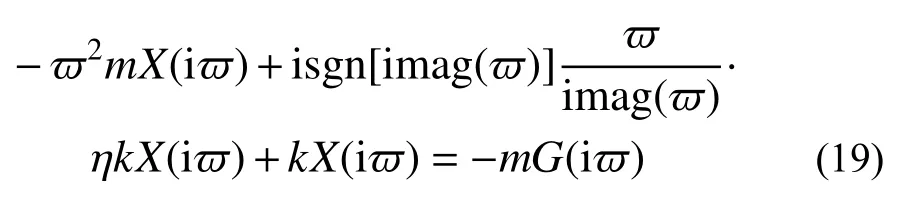
显然， ϖ为复频率时，在频域内定义运动方程是不准确的，此时，采用复数域内的拉氏运动方程表示改进滞变阻尼模型是更符合实际情况的做法，借助于拉普拉斯变换，构建复数域内的改进滞变阻尼模型运动方程为：

式中：X(s) 为x(t)的拉普拉斯变换；G(s) 为g(t)的拉普拉斯变换。

采用拉普拉斯逆变换，可得到改进滞变阻尼模型的时域运动方程为：

式中， ϖv为结构动力响应的振动频率。

式(21)对应的自由振动方程为：

对式(22)进行拉普拉斯变换后，可得：

式(23)包含符号函数和虚部函数，求解X(s)是困难的，因此，可采用特征值法求解式(22)。

改进滞变阻尼模型的特征值方程为：

令：

将式(25)代入式(24)，可得：

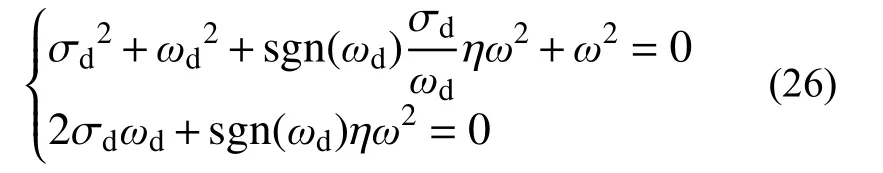
求解式(26)，可得：

进一步得到2 个共轭特征值为：

依据特征值和常数变易法，可得到对应的自由振动响应表达式为：

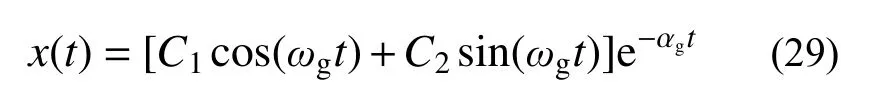
其中：

由式(29)和式(30)可知，本文基于复数域内的拉氏运动方程创建的改进滞变阻尼模型的自由振动响应中不包含发散项，时域计算结果是稳定收敛的，可克服复阻尼模型的缺陷；随着损耗因子的增加，有阻尼自振频率 ωg随着损耗因子的增加而逐渐减小，可克服传统滞变阻尼模型的缺陷。

2 改进滞变阻尼模型的时域计算方法

对于基于改进滞变阻尼模型的比例阻尼体系，可直接采用传统的实模态叠加法，将多自由度体系运动方程分解为单自由度体系运动方程，进而采用实模态叠加实现动力响应的时域计算。对于基于改进滞变阻尼模型的非比例阻尼体系，可将多自由度体系运动方程转化为复数域内拉氏运动方程，进一步采用复模态叠加法将多自由度体系运动方程分解为单自由度体系运动方程，进而采用复模态叠加实现动力响应的时域计算。因此，为求解基于改进滞变阻尼模型的单自由度体系时域运动方程，本文分别提出基于傅里叶变换和希尔伯特-黄变换的单自由度体系动力响应的时域计算方法。

2.1 基于傅里叶变换的时域计算方法

基于改进滞变阻尼模型的时域运动方程中包含有振动频率的未知项，因此，无法通过常用的时程计算方法包括常平均加速度法、Newmark-β法、中心差分法等逐步积分法[1-2]计算其时域动力响应。为此，采用快速傅里叶变换法，将外激励加速度用傅里叶级数展开[36]，可得：

将式(31)代入式(21)，可得：

令式(32)的一般解为：

式中：xc(t)为式(32)对应的齐次方程通解；xp(t)为式(32)对应的非齐次方程特解。

令：

将式(33)和式(34)代入式(32)，可得：

式中：xc(t)为式(35)的通解；xp,0(t)为式(36)的特解；xp,n(t)为式(37)的特解。

式(35)的通解与自由振动响应相同，可表示为：

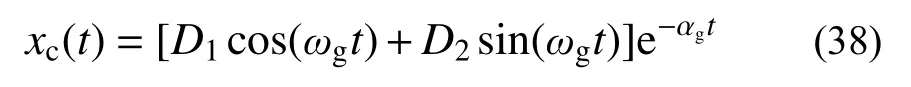
式中， D1和 D2为待定系数。

式(36)的特解为：

令式(37)的特解为：

将式(40)代入式(37)，可得：

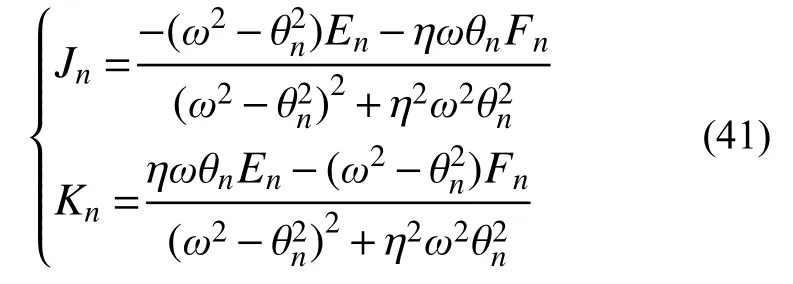
由式(38)～式(41)可得到式(32)的一般解为：

其中：

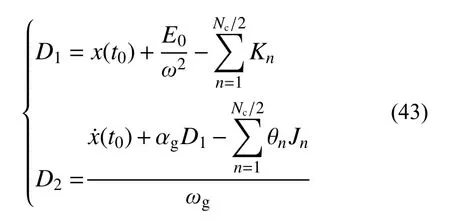
综上，由式(42)可实现基于傅里叶变换的动力响应时域计算方法。该方法是一种全局过程的计算方法，可计算出任意时刻的结构动力响应，且无条件稳定收敛。基于傅里叶变换的时域方法可在MATLAB 软件平台上通过编程实现，对应的算法流程如图1 所示。

图 1 基于傅里叶变换的时域方法流程图Fig.1 Flow chart of the proposed time-domain method based on Fourier transform

2.2 基于希尔伯特-黄变换的时域计算方法

首先将时间离散化，即按照步长 Δt对时间进行离散，任意时刻可表示为tk=kΔt(k=0,1,2,···)。采用希尔伯特-黄变换法[37]对外激励加速度进行识别分析，由经验模态分解(EMD)将外激励加速度分解为s 条本征模函数(imf)和残余分量，进一步利用希尔伯特变换识别出imf 的瞬时频率、瞬时振幅等信息。由此， tk时刻到tk+1时刻，外激励加速度可表示为：

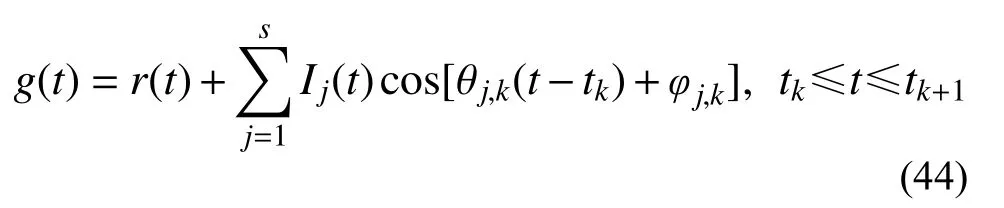
式中： θj,k为第j 条imf 分量 tk时刻到tk+1时刻的瞬时频率； φj,k为第j 条imf 分量tk时刻的瞬时相位；Ij(t)为第j 条imf 分量的瞬时振幅；r(t)为残余分量。

第j 条分量tk+1时刻的瞬时相位可表示为：

将式(44)代入式(21)，可得：

令式(46)的一般解为：

式中：xc(t)为式(46)对应的齐次方程通解；xp(t)为式(46)对应的非齐次方程特解。

令：

将式(47)和式(48)代入式(46)，可得：

式中：xc(t)为式(49)的通解；xp,0(t)为式(50)的特解；xp,j(t)为式(51)的特解。

式(49)的通解与自由振动响应相同，可表示为：

式(50)的特解为：

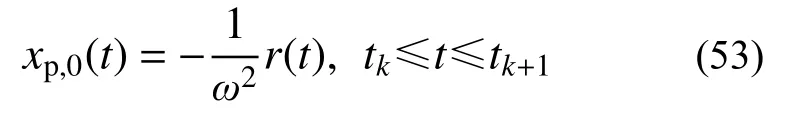
令式(51)的特解为：

将式(54)代入式(51)可得：

求解式(55)，可得：

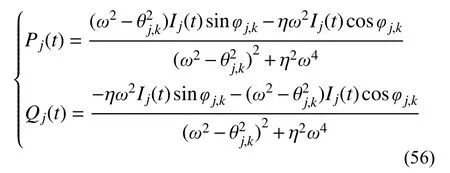
将式(52)～式(56)代入式(47)，可得tk+1时刻结构的位移为：

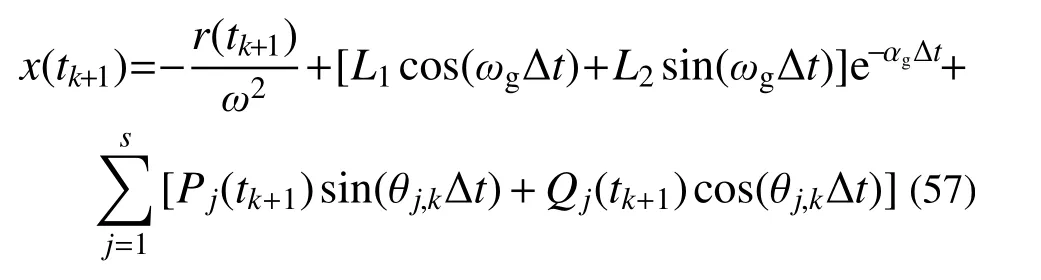
tk+1

由式(57)可进一步得到 时刻结构的速度为：

式中：

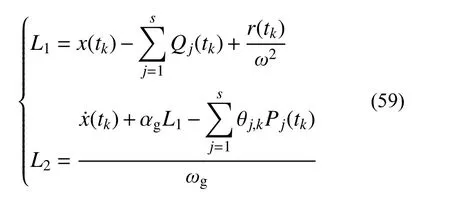
依据式(57)～式(59)，可由 tk时刻结构的位移和速度计算出tk+1时刻的结构响应，从而实现了基于希尔伯特-黄变换的动力响应时域计算方法。该方法是一种时域逐步计算方法，同时也是无条件收敛的。基于希尔伯特-黄变换的时域方法可在MATLAB软件平台上通过编程实现，对应的算法流程如图2所示。

图 2 基于希尔伯特-黄变换的时域方法流程图Fig.2 Flow chart of the proposed time-domain method based on Hilbert-Huang transform

3 算例分析

3.1 谐波作用下的时域精确计算方法

随机激励可近似视为谐波的叠加，因此分析谐波作用下结构的动力响应具有代表性。以两条谐波组合得到的外激励信号为例，对比分析本文提出的时域计算方法。

采集到的外激励信号通常情况下是离散的，按照步长 Δt对时间进行离散，任意时刻可表示为tk=kΔt(k=0,1,2,···)。外激励加速度可表示为：

式中：

式中：h1(t) 和h2(t)分别为第一谐波分量和第二谐波分量的振幅函数； φk和 φk分别为第一谐波分量和第二谐波分量 tk时刻的相位；φk+1和φk+1分别为第一谐波分量和第二谐波分量tk+1时刻的相位；q1(t) 和q2(t)分别为第一谐波分量和第二谐波分量的振动频率函数。

与基于希尔伯特-黄变换的时域计算方法相同，依据外激励加速度的表达式，采用齐次方程通解和非齐次方程特解分别求解并叠加计算的方法，可得到谐波作用下改进阻尼模型的时域精确计算结果。

3.2 算例1

以损耗因子为0.5，自振频率为30 rad/s 的单自由度体系为例，对体系作用外激励R-1，激励作用时间为15 s。外激励R-1 的具体参数为：外激励加速度的采样频率为100 Hz，对应的时间步长Δt为0.01 s，第一谐波分量和第二谐波分量的参数见式(63)，外激励R-1 的加速度时程如图3 所示。

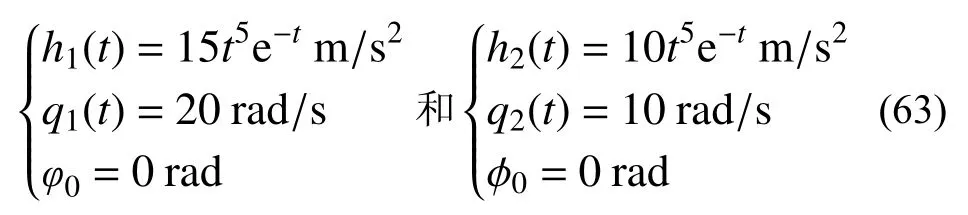
考虑到快速傅里叶变换法对采样点数的要求，首先对外激励信号进行补零处理[1](下同)。随后，对外激励R-1 进行快速傅里叶变换，可得到对应的傅里叶变换谱如图4 所示，表明其可准确识别出外激励R-1 中两条谐波的频率。

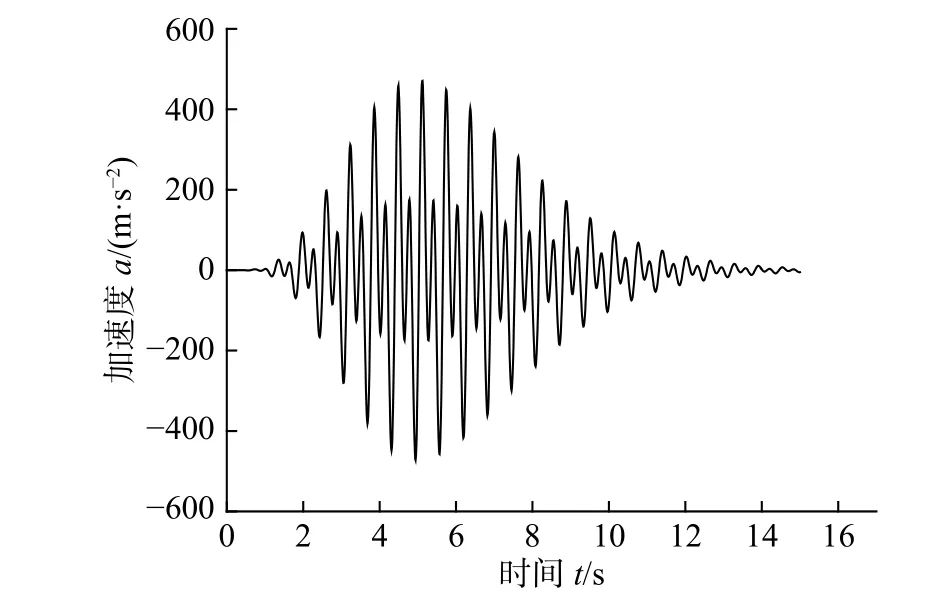
图 3 外激励R-1 的加速度时程Fig.3 Acceleration time-history of external excitation R-1

图 4 外激励R-1 的傅里叶变换谱Fig.4 Fourier transform spectrum of external excitation R-1

考虑到希尔伯特-黄变换的端点效应问题，采用正弦波法对[38-39]外激励R-1 的两端进行延拓处理，进而对外激励R-1 进行EMD 计算，当残余分量为单调函数或最大值小于0.05 m/s2时停止分解[37,40](下同)。由外激励R-1 的EMD 结果可知，imf1 和imf2 是主要分量，imf1 对应的瞬时振幅和瞬时频率，与外激励R-1 中第一条谐波分量(hw1)的瞬时振幅和瞬时频率近似相等(见图5(a)和图6(a))；imf2 的瞬时振幅和瞬时频率则与外激励R-1 中第二条谐波分量(hw2)的瞬时振幅和瞬时频率近似相等(见图5(b)和图6(b))。因此，希尔伯特-黄变换法可准确识别出外激励R-1 中两条谐波的振幅和频率。

图 5 外激励R-1 的瞬时振幅对比Fig.5 Comparison of instantaneous amplitudes of external excitation R-1

图 6 外激励R-1 的瞬时频率对比Fig.6 Comparison of instantaneous frequencies of external excitation R-1

分别采用基于傅里叶变换的时域计算方法(IF)、基于希尔伯特-黄变换的时域计算方法(IH)和时域精确计算方法(IP)计算该算例单自由度体系的加速度时程，结果如图7 所示。IF、IH 和IP 计算的结构加速度时程近似相等(见图7)，IF和IH 的加速度峰值相对误差都小于5%(见表1)，证明了IF 和IH 的正确性。IF 是一种全局过程的计算方法，可计算任意时刻的结构动力响应，不用进行时域逐步计算，结果更为直观。IF 利用快速傅里叶变换将任意外激励信号分解为一系列三角函数分量和常数分量，仅产生较小的近似误差，对应的数学证明是严谨的。但IF 的计算耗时远大于IH(见表1)，这是因为外激励信号进行傅里叶变换时，需要分解为Nc/2 条谐波，IH 进行希尔伯特-黄变换时仅分解为8 条信号分量。相比IF，IH 是一种时域逐步计算方法，计算结果依赖于前一时刻的结果；同时希尔伯特-黄变换法中存在端点效应，为初始时刻的计算结果引入了误差，并随着时域逐步计算影响整个过程的计算精度。由于目前常用的端点效应处理方法并不能完全消除端点效应的影响，导致IH 的计算误差不易估计。此外，EMD 分解法和端点效应消除方法是一种经验分解方法，导致IH 缺乏严谨的数学理论支持。

图 7 外激励R-1 作用下的结构加速度时程响应Fig.7 Structural acceleration responses time-history under external excitation R-1

表 1 外激励R-1 作用下结构的动力响应对比Table 1 Comparison of structural dynamic responses under external excitation R-1

3.3 算例2

采用与算例1 相同的单自由度模型，对体系作用外激励R-2，激励作用时间为15 s。外激励R-2的具体参数为：外激励加速度的采样频率为100 Hz，对应的时间步长 Δt为0.01 s，第一谐波分量和第二谐波分量的参数见式(64)，外激励R-2 的加速度时程如图8 所示。

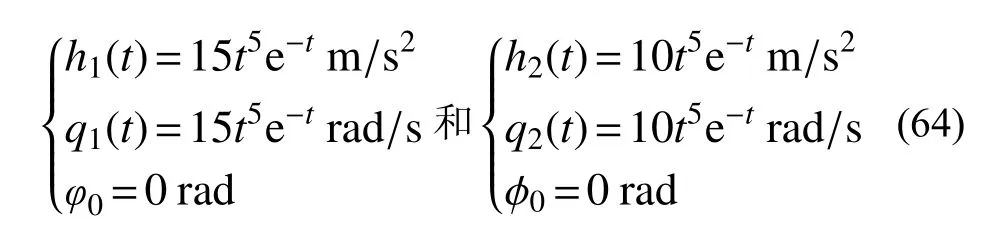
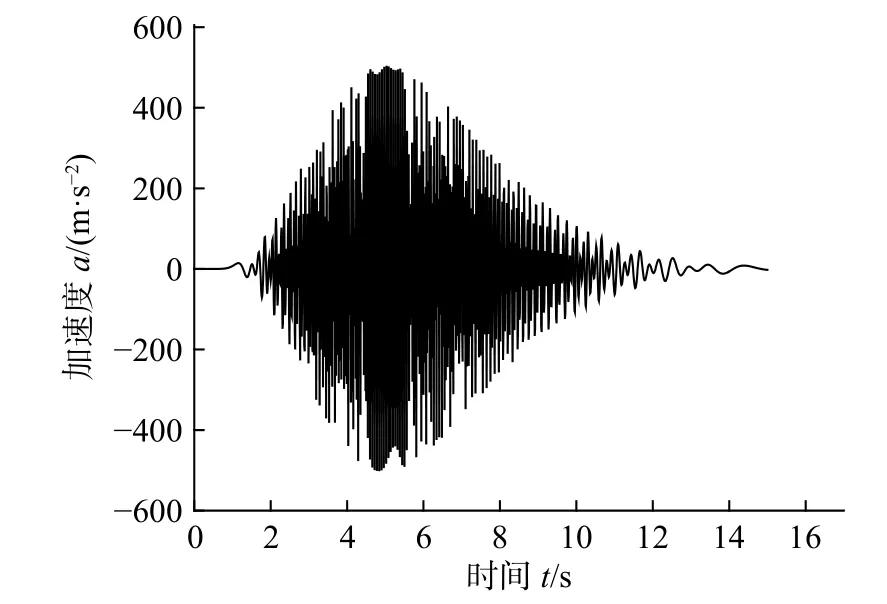
图 8 外激励R-2 的加速度时程Fig.8 Acceleration time-history of external excitation R-2

与算例1 不同，算例2 的外激励R-2 的两条谐波的瞬时频率是变化的。计算结果表明：由于傅里叶变换法是从能量角度对外激励信号进行分解，对于随时间变化的瞬时频率，不能进行准确识别，仅能确定外激励R-2 的频率范围(见图9)。相比傅里叶变换法，希尔伯特-黄变换法可识别出外激励R-2 中谐波分量的瞬时振幅和瞬时频率。由外激励R-2 的EMD 结果可知，imf1 和imf2 是主要分量，可对比分析imf1 和hw1、imf2 和hw2的瞬时振幅和瞬时频率，结果如图10 和图11所示。

图 9 外激励R-2 的傅里叶变换谱Fig.9 Fourier transform spectrum of external excitation R-2

分别采用IF、IH 和IP 计算外激励R-2 作用下体系的加速度时程，结果如图12 所示。表2 所示，与算例1 的计算结果相比，IF 和IH 的计算精度都有所下降，IF 的加速度峰值相对误差由0.42%增加到25.20%，IH 的加速度峰值相对误差由1.28%增加到9.00%。与恒定频率的外激励R-1 相比，希尔伯特-黄变换法对具有瞬时变化频率的外激励R-2 的识别精度有所下降，但可粗略识别出其变化趋势。相比IF，IH 的计算量更少、计算精度更高。傅里叶变换方法受限于W.Heisenberg 不确定准则，无法有效识别出外激励信号的瞬时频率等信息，而希尔伯特-黄变换方法具有自适应性，可有效识别出任意非平稳外激励信号的瞬时信息。因此，与IF 相比，IH 具有更宽泛的适用范围。

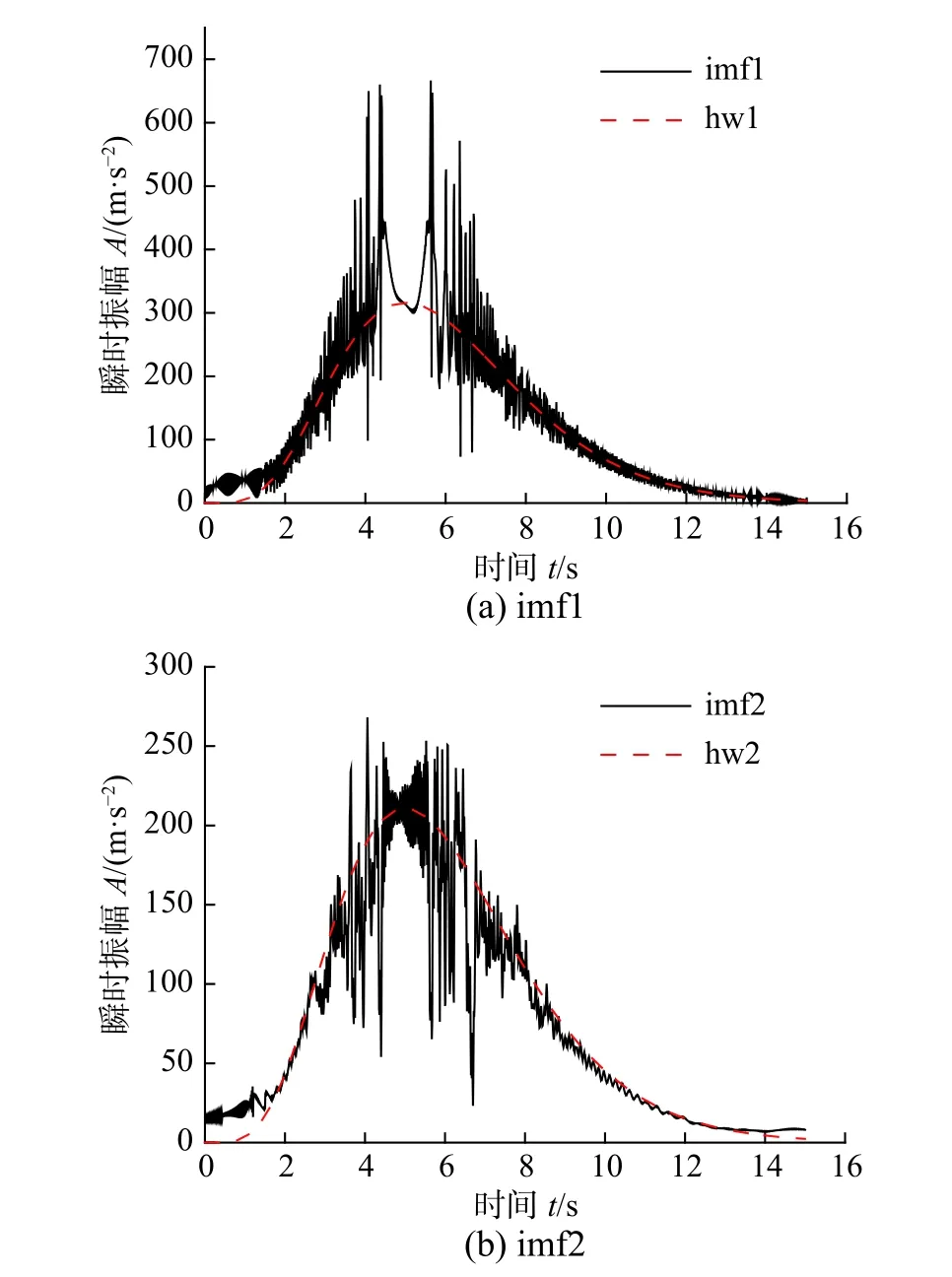
图 10 外激励R-2 的瞬时振幅对比Fig.10 Comparison of instantaneous amplitudes of external excitation R-2

图 11 外激励R-2 的瞬时频率对比Fig.11 Comparison of instantaneous frequencies of external excitation R-2

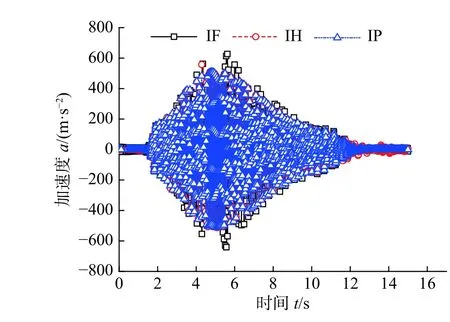
图 12 外激励R-2 作用下的结构加速度时程响应Fig.12 Structural acceleration responses time-history under external excitation R-2

表 2 外激励R-2 作用下结构的动力响应对比Table 2 Comparison of structural dynamic responses under external excitation R-2

3.4 算例3

以损耗因子为0.5 的多自由度体系为例，质量刚度分布如图13 所示。对体系作用外激励R-2，激励作用时间为15 s，结合模态叠加法，可分别采用IF、IH 和IP 计算外激励R-2 作用下体系顶层的加速度时程，结果如图14 所示。表3 所示，IF 的加速度峰值相对误差为25.17%，IH 的加速度峰值相对误差为4.05%。与算例2 的计算结果规律一致，IF 的相对误差最大，且计算时间最长。

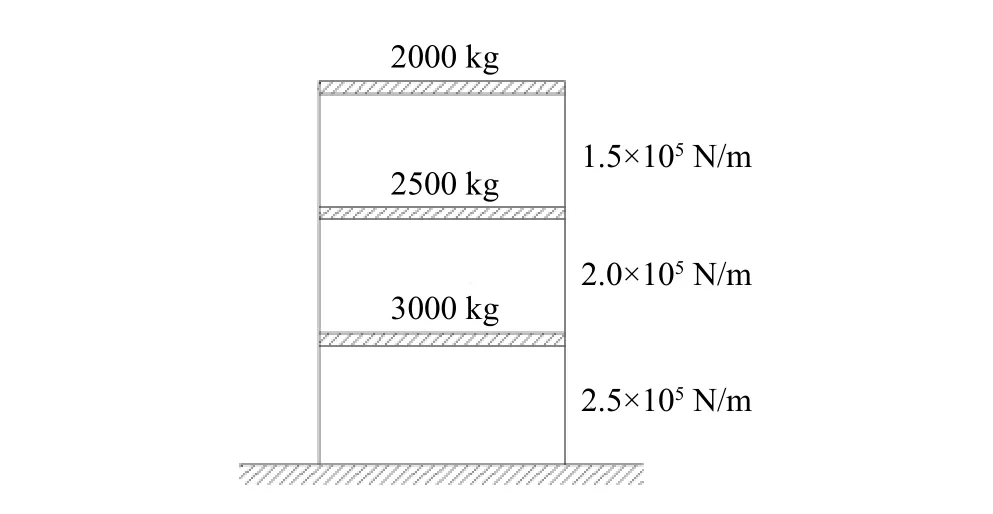
图 13 模型示意图Fig.13 Schematic of model

图 14 外激励R-2 作用下的结构顶层加速度时程响应Fig.14 Structural top acceleration responses time-history under external excitation R-2

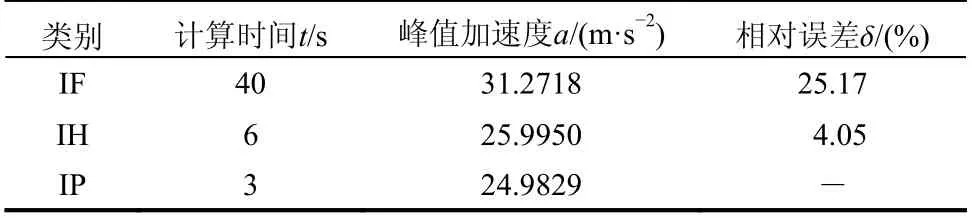
表 3 外激励R-2 作用下结构顶层的动力响应对比Table 3 Comparison of structural top dynamic responses under external excitation R-2

4 讨论

通过分析改进滞变阻尼模型的特点，并对比基于傅里叶变换的时域计算方法和基于希尔伯特-黄变换的时域计算方法可知：

(1)改进滞变阻尼模型的阻尼矩阵构造容易，仅依赖于材料损耗因子和结构刚度矩阵，在后续研究中可更方便地用于非比例阻尼体系的动力响应分析，如设置了耗能阻尼器的建筑结构等。

(2)基于改进滞变阻尼模型的时域计算方法的缺陷来源于信号识别方法的局限性。相比傅里叶变换法、小波变换法，希尔伯特-黄变换法可以更加准确地识别振动频率与时间的关系，但常用的端点效应处理法和EMD 分解法存在缺陷。在后续研究中，可采用优化极值延拓、神经网络预测等方法减小端点效应；可采用多项式曲线、B 样条曲线、幂函数曲线等代替传统样条曲线进行插值，以提高计算精度。

5 结论

本文依据基于复阻尼模型的改进滞变阻尼模型，提出了不同的时域计算方法，并通过算例分析得出如下结论：

(1)在复阻尼模型的基础上，提出了基于复阻尼模型的改进滞变阻尼模型，创建了对应的复数域内拉氏运动方程和时域运动方程。改进滞变阻尼模型不仅克服了复阻尼模型的时域计算发散缺陷，还克服了滞变阻尼模型的有阻尼自振频率随损耗因子增加而增加的缺陷。依据外激励加速度的识别方法，分别提出了基于傅里叶变换、基于希尔伯特-黄变换的时域计算方法。

(2)基于傅里叶变换的时域计算方法是一种全局过程的计算方法，可直接计算任意时刻的结构动力响应，但计算量较大，且无法识别瞬时频率。求解频率随时间变化的外激励作用下结构动力响应时，其计算精度较低。

(3)基于希尔伯特-黄变换的时域计算方法是一种时域逐步积分算法，计算量较小、适用范围更广。EMD 分解和端点效应影响外激励加速度的识别精度，导致该方法的计算误差不易估计。