弱耦联体系地震响应的隔离分析求解

2021-04-21文嘉意

工程力学 2021年4期

文嘉意，谢强

(同济大学建筑工程系，上海 200092)

弱耦联体系多见于能源电力领域，通常由若干支柱式设备以及连接它们的柔性连接件构成，如图1 中实例所示。由于近年来地震灾害对电力系统造成了较严重的损失[1-3]以及我国特高压等重要电力设施在高地震烈度地区的广泛建设[4-5]，弱耦联设备体系的抗震研究日益受到关注[6-7]。

图 1 弱耦联体系实例Fig.1 Examples of weakly-coupled system

在建筑工程领域，目前有许多针对连体结构、相邻结构振动特性的研究[8-10]。弱耦联体系虽在直观上类似于连体结构，但其主要区别在于：1)研究表明，耦联作用对体系地震响应有明显影响，不可忽略[11-12]。但柔性连接件约束作用弱，体系的结构整体性差、整体振型不明显[13]。地震作用下各设备的响应仍由其自身动力特性主导[14]。建筑结构通常要求整体性良好，子结构间具有协同性，一般在概念设计阶段便回避了这一问题；2)体系中设备与连接件材料的阻尼特性差异大。例如，图1 中支柱设备通常为陶瓷或复合绝缘材料[15]，而连接件则为金属导电材料。这意味着目前抗震计算中常用的比例阻尼[16](即通过整体质量、刚度矩阵线性组合生成的阻尼矩阵)难以兼顾体系各部分的实际阻尼特性。

目前弱耦联设备体系抗震基本沿用了建筑抗震规范中的通用计算方法[17-18]，即基于整体振型与比例阻尼的叠加法和作为补充计算的时程法。在采用前者进行计算时，上述两个问题的存在有可能造成一定的系统误差；而时程法由于弱耦联体系体量较大且同一体系中设备、连接件的形式多样，无标准构型，建模与计算成本往往偏高。

目前有学者研究了考虑非比例阻尼的耦联体系抗震计算方法，但其求解仍然依靠于体系的整体振型[19]。本文则从隔离体分析出发，充分考虑体系各子结构自身动力特性，并在频域进行求解，从而避免了对体系整体振型以及比例阻尼的使用。

1 基于隔离体的理论分析模型

1.1 整体求解思路

根据弱耦联体系的结构特征，理论分析基于如下几条主要假定：

① 由于连接件弯曲刚度远小于支柱设备，因此连接件作用于支柱的弯矩忽略不计；

② 实际中的弱耦联体系一般在两个水平正交方向进行布置。由于连接件柔度很大，难以传递体系的整体扭转，因此本文理论模型忽略水平双向地震的扭转耦合作用，将空间体系在两水平正交方向上拆解为平面结构进行计算。实际应用中，将不同方向上的地震响应计算结果进行叠加即可；

③ 当体系中支柱存在高度差或者非等张拉连接时，耦联作用力将产生竖向分量。但一方面，由于弱耦联体系中耦联作用力以及连接件质量均较小，竖向分量对工程中实际关注的水平地震响应的影响可忽略。另一方面，由于本文在广义线性框架内构建支柱以及连接件的隔离体运动方程，高度差以及非等张拉连接均不改变最终求解式的形式。因此为了表达的简洁性，本文按照等高度、等张拉连接这一实际中更为普遍的情况进行理论建模与推导。

采用如图2 所示的简化模型进行理论求解。图2 中第i 号支柱式设备(以下简称“支柱i”)的线密度与刚度分别为mi(y) 与EIi(y)，受到地震作用x¨ig(t)，其位移为υi(y,t)。因为避免使用结构整体振型，因此不直接建立整体结构矩阵，而采用隔离体分析。支柱i 及其两侧连接件进行隔离可由图3 表示。

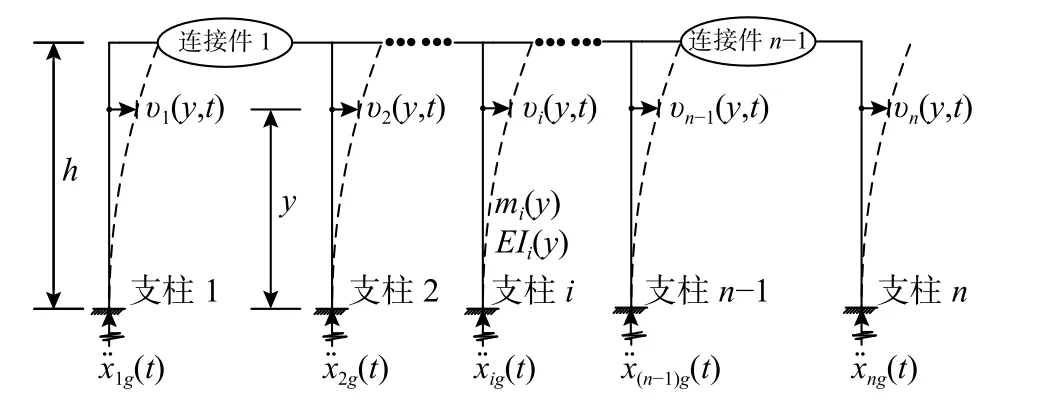
图 2 弱耦联体系理论计算简图Fig.2 Analytical diagram of a weakly-coupled system

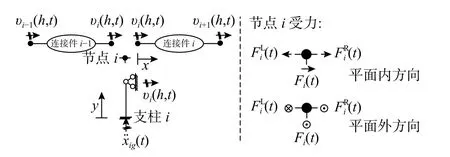
图 3 弱耦联体系隔离体图Fig.3 Free-body diagram of a weakly-coupled system

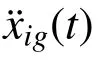
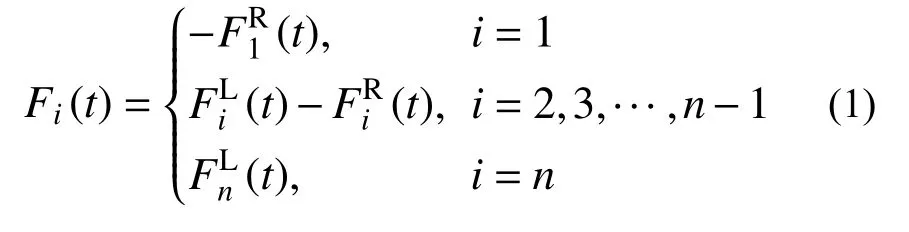
对任意类型的支柱以及连接件，上述作用力与支座激励间必定满足如下的映射关系：

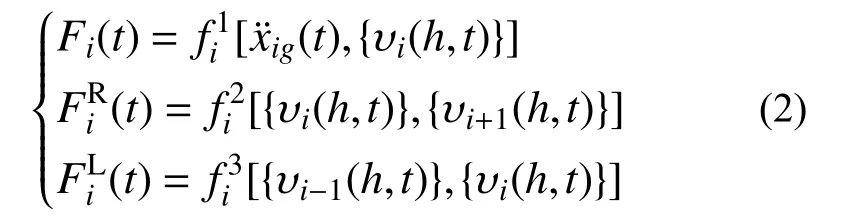
式中，H (ω)为广义传递矩阵，具有如式(5)所示的表达式(式中(ω)已省略)：

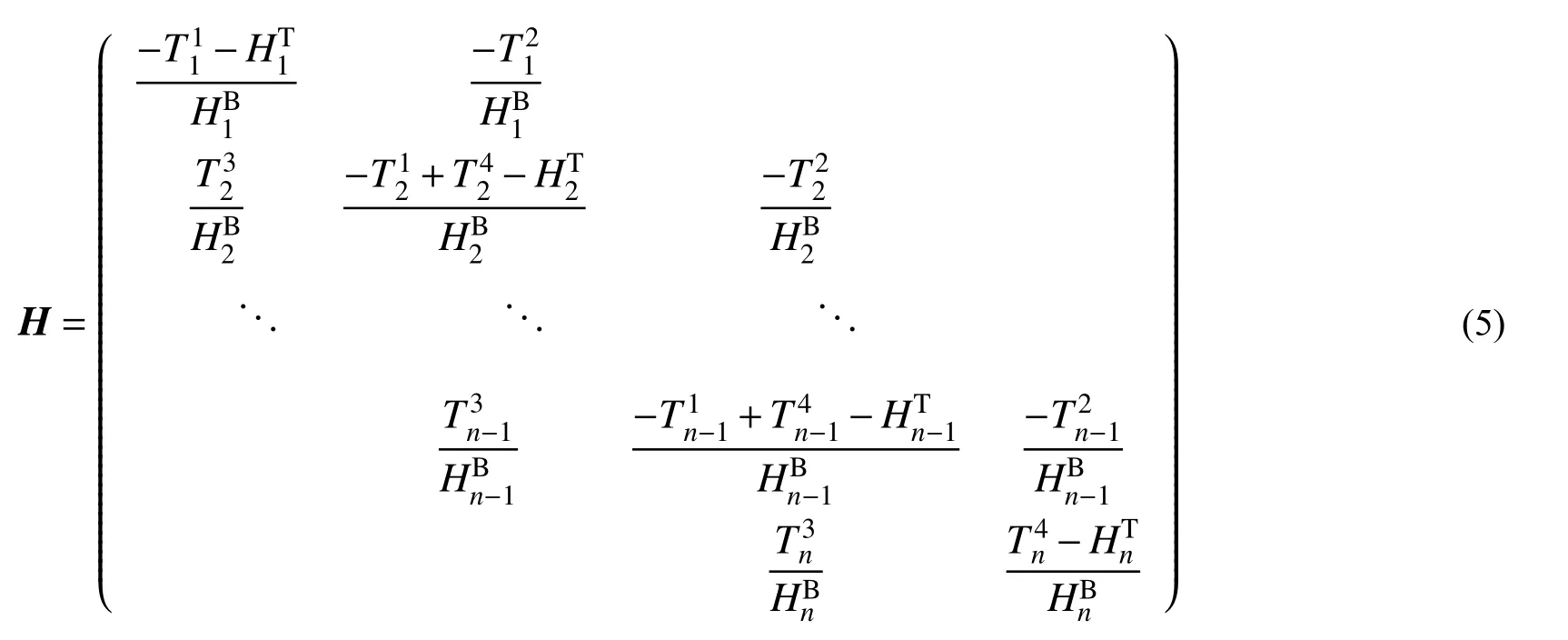
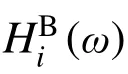
1.2 支柱隔离体分析

隔离后的支柱i 在如图3 所示的支座激励下，可利用结构动力学经典弯曲梁动力理论进行推导，得到其顶端支座反力-位移控制方程为：

需要特别提到的是，振型函数φij(y)并非采用体系整体的结构特性矩阵求得的整体振型，而是指图3 中支柱i 隔离体的第j 阶振型函数。而对广义坐标zij(t)，容易推导其满足如下的运动方程：

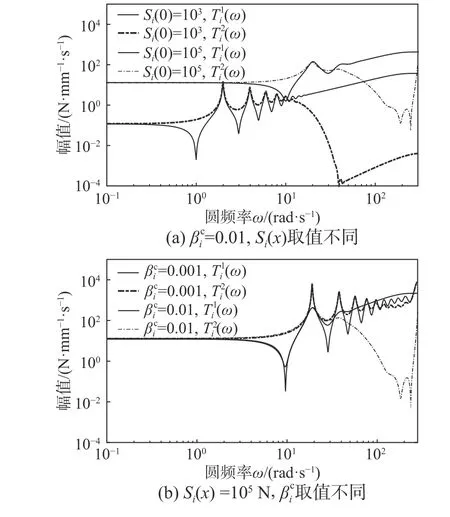
图 4 线性连接件传递函数示例Fig.4 Transfer functions of exampled linear connections

至此即完成了对支柱以及连接件隔离体力-支座激励控制方程的推导，实现了式(3)的显式化表达，理论上可对弱耦联设备体系的地震响应进行求解。接下来通过实例对理论推导进行验证。

2 弱耦联设备体系实例验证

上面基于隔离分析，推导了弱耦联体系地震响应的解法。下面拟通过典型弱耦联设备体系实例的振动台试验验证该解法，并与振型叠加法求解进行对比，进一步研究弱耦联特性的影响。

2.1 试验对象及试验概述

试验对象为变电站常见的采用滑动管母线连接的支柱绝缘子体系，如图5(a)所示，并规定水平平面内、外方向分别为X 向、Y 向，竖直方向为Z 向。两支柱绝缘子安装在两个6 m×3 m 的振动台组成的台阵上，间距为8.5 m。振动台包括两个水平正交方向以及竖直方向上的三个自由度，输入频率范围为0.1 Hz ～50 Hz。

图 5 滑动管母线连接的支柱绝缘子振动台试验Fig.5 Shaking table test of post insulators connected by slidable busbar

支柱1、2 结构上完全相同，包括底部5 m 高的格构式钢支架(Q235 材质)以及上部五段复合材料绝缘子(实心圆截面，直径280 mm)。每段绝缘子均由两侧金属法兰以及中间双层玻璃钢芯棒组成。芯棒内、外两层玻璃钢弹性模量分别为53.95 GPa、15.63 GPa，结构总高度为17.27 m，总重为4055 kg。支柱在顶端通过金具与滑动管母线连接。另外，为了模拟电气元件等非结构构件的惯性作用，支柱1、2 顶部分别附有集中配重198 kg、147 kg。

滑动管母线为空心铝制圆管(φ 300×12 mm)，重347 kg，其左侧与支柱1 顶端固定，右侧与支柱2 顶端之间采用如图5(b)所示的滑动金具连接。滑动金具为一铝制圆环，安装时管母线自由插入，与圆环之间无预紧及嵌固。这样的连接方式仅约束Y 向、Z 向运动，管母线可沿X 向自由滑动，因此实际连接刚度远小于管母线截面刚度，为典型柔性连接。滑动管母线在如图5(b)所示滑动端伸出了1.3 m 的冗余距离，以保证其自由滑动，不发生脱出。

主要通过试验加速度及位移响应对本文解法进行验证，因此在各段绝缘子端部均布置了三向加速度传感器(图5 中A1～A12)。由于试验对象高达17.3 m，难以通过位移计对位移进行实测，因此通过实测加速度的逐步积分计算位移响应。另外，在两支柱根部均布置了应变计测量绝缘子应变响应。

根据白噪声扫频结果，未连接管母线以及顶部配重的支柱在X 向、Y 向的前两阶频率均为0.659 Hz 以及4.370 Hz。组成耦联体系后，支柱1、2 在X 向基频均为0.641 Hz，而二阶频率出现了差异，分别为4.311 Hz 以及4.143 Hz。在Y 向，两支柱绝缘子前两阶频率均为0.649 Hz 以及4.260 Hz。耦联体系两支柱X 向二阶频率的差异说明在此频率附近两支柱的振动并不协同，整体的二阶振型响应不明显，体现了弱耦联特性，因此主要从X 向响应对理论计算进行验证。

2.2 输入地震动

试验工况如表1 所示，输入地震动包括2 条天然波：El-centro 波、Taft 波以及1 条人工波。地震动输入前后均进行了白噪声扫频测试。试验中振动台三向激振，以X 向(平面内方向)为主振方向，峰值地面加速度(PGA)在X 向、 Y 向和 Z 向之比为1∶0.85∶0.65。试验强震工况下，X 向PGA 为0.4 g；强震工况前，在X 向PGA 大约为0.2 g 的水平下进行了地震动迭代输入，以校准振动台输入参数。在2%阻尼比下，三条地震波X 向反应谱以及电力设施抗震规范[15]给出的目标谱如图6 所示。为方便参考，耦联体系中支柱1 的前两阶自振频率也在图6 中标出。

对于地震波的选取，一方面由于试验支柱绝缘子的柔性较大，基频在1 Hz 以下，地震动中的低频成分对其影响较大。所选人工波在平台段以外的低频区也能较好地覆盖目标谱。另一方面，耦联体系在二阶振型表现出弱耦联的特点，Taft波以及人工波反应谱在该二阶频率处均有明显峰值，可充分考察弱耦联特性。

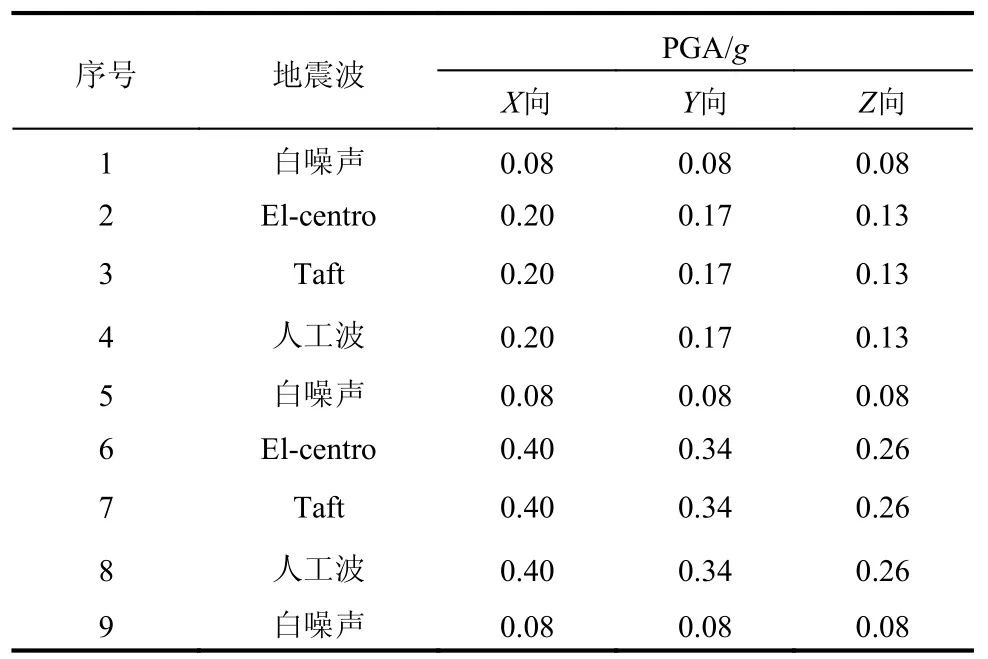
表 1 试验工况Table 1 Scenarios of testing

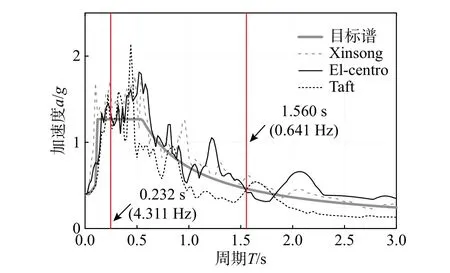
图 6 试验输入地震波反应谱Fig.6 Test response spectra of input ground motions

2.3 模型参数确定

注意到，1.3 节在建立连接件在频域的力-位移控制方程时，对连接件提出了“线性或可等效为线性”这一先决条件。而滑动管母线无法直观判断可否等效为线性连接，首先需要进行验证。验证手段即通过试验中支柱的实际顶端位移以及耦联作用力反推出二者在频域的传递函数。如果其形式与图4 中曲线一致，且能用式(14)的理论曲线进行有效拟合，则说明试验对象可等效为线性耦联。同时，这一验证流程也可确定理论模型计算中所需参数。

虽然在试验中无法直接测量管母线作用力，仍可通过试验的加速度及应变响应近似计算出耦联作用力。例如对支柱1，其根部弯矩M1(t)近似满足：

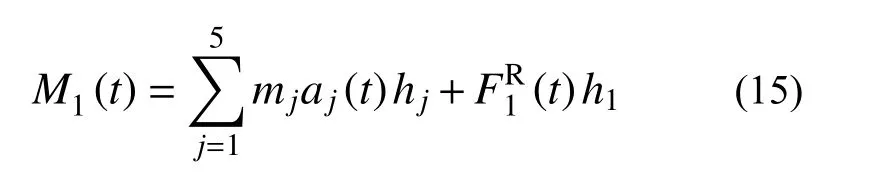
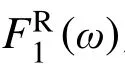
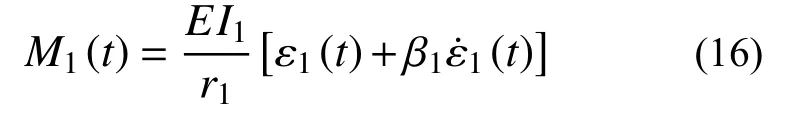
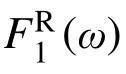
对匀质的线性连接件，容易证明：

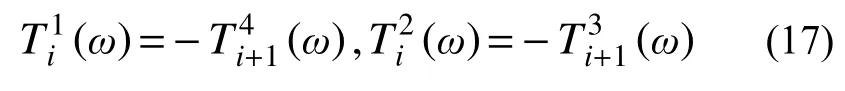
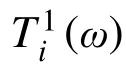
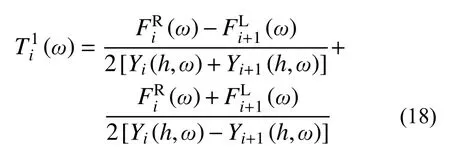
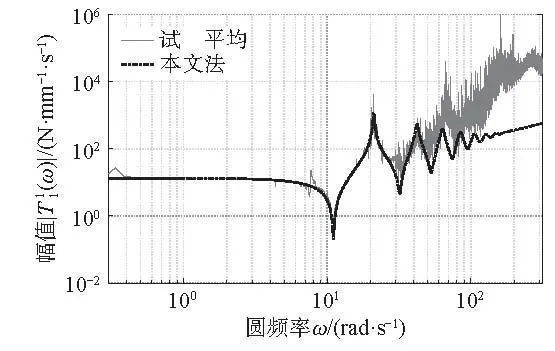
图 7 |的试验及理论计算结果Fig.7 Experimental and analytical results of

2.4 结果对比

在确定了模型参数后，采用本文方法计算体系的X 向地震反应。计算得到的支柱顶端对地相对位移d 与试验结果拟合度高，例如图8 展示了人工波输入下本文方法计算结果与试验结果的时程对比。

图 8 人工波输入下支柱顶部相对位移试验及理论结果Fig.8 Experiment and analytical relative displacement at top of post insulators with the artificial wave

同时，也采用基于整体振型的振型叠加法(以下简称“叠加法”)进行了计算，计算除采用比例阻尼外其余模型参数均与本文方法相同。基于体系整体的前两阶自振频率以及实测的1.5% 阻尼比，可求得比例阻尼参数。三条地震动输入下，本文方法与叠加法计算的支柱顶部相对位移误差Δd 如图9 所示。本文方法计算的误差显著小于叠加法，且误差在整个地震持时内都较为稳定，无明显突出。

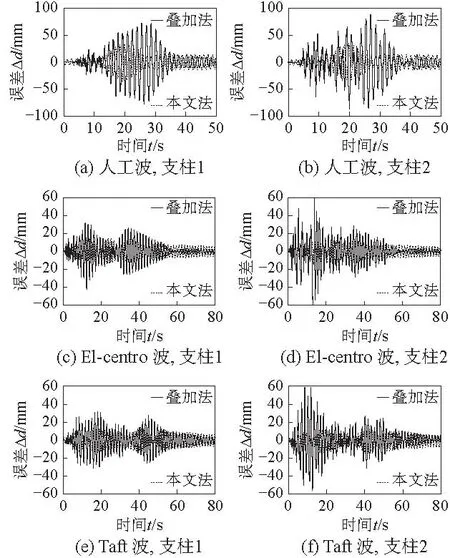
图 9 本文法与叠加法顶部相对位移误差Fig.9 Errors of the relative top displacement with the proposed method and the superposition method

由于电气设备对位移响应十分敏感，因此需关注体系的最大位移。表2 列出了两种计算方法下支柱顶部沿X 向(即平面内方向)的最大相对位移和误差。在所有情况下本文法结果均略高于实际；而叠加法结果则表现出系统性误差，即任一地震输入下均高估一支柱响应而低估另一支柱响应。尤其是Taft 波及人工波，最大误差均超过-10%，在表2 中进行了加粗表示。这主要是因为叠加法无法考虑体系在二阶振型处出现的弱耦联特性，而图6 中Taft 波以及人工波恰好在体系二阶频率处有明显峰值，因此高估了连接件耦联作用，这将在下一节展开探讨。

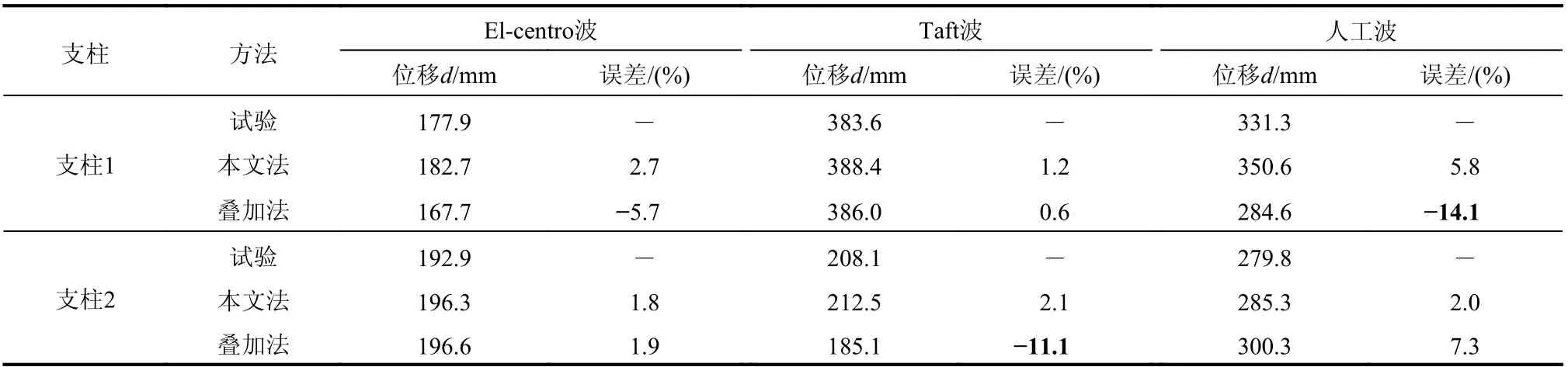
表 2 不同方法下支柱绝缘子顶部最大相对位移Table 2 Maximum relative displacement at top of insulator posts with different methods

3 弱耦联特性的进一步探讨

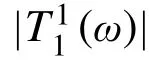
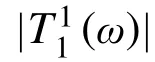
图11 为人工波输入下本文法与叠加法支柱顶部加速度的傅里叶幅值谱，二者主要存在两大差别。第一，本文法结果在2 Hz～10 Hz 成分并不明显，仅在第二振型，即4.3 Hz 处有一较小峰值。而叠加法在2 Hz～10 Hz 有显著成分，反映了对弱耦联体系采用整体振型进行计算，会高估某些振型响应。由于连接件的约束弱，在实际地震作用下，一些振型响应并不会被明显激发；第二，本文法中两支柱频谱在基频处峰值不同，反映了两支柱顶端的实际运动并不一致。而叠加法中两曲线基本吻合，这说明叠加法高估了实际耦联作用，强化了两支柱间的约束使得二者运动协调一致。这也是表2 中叠加法总是高估一支柱位移而低估另一支柱位移的原因。

图12 中两支柱顶部绝对位移d1、d2的散点图可进一步证明。由于试验对象采用滑动管母线，自由滑动下两支柱位移散点图应呈现出平滑曲线。未采用整体振型而基于隔离体分析的本文法在图12(a)中体现了这一点。而图12(b)中叠加法曲线的波折以及整体轮廓的萎缩则明显反映出叠加法高估了实际耦联作用，两支柱间相对滑动的约束作用明显。

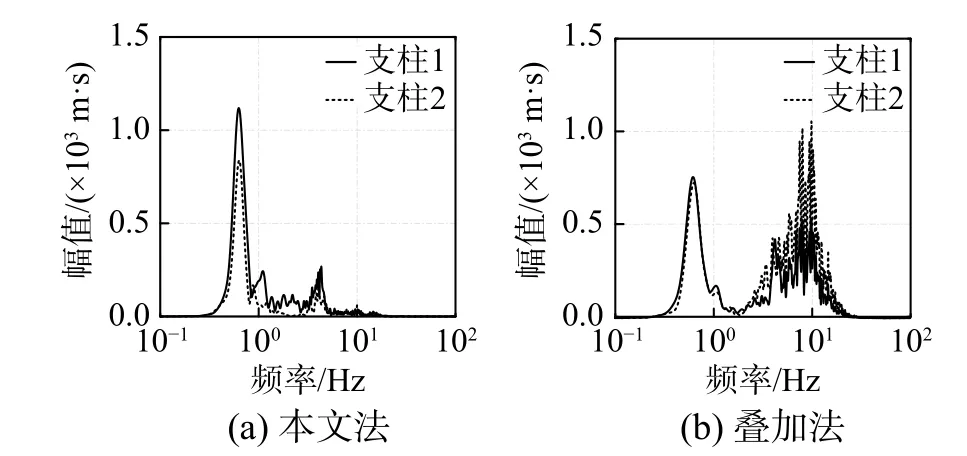
图 11 人工波下支柱顶部加速度傅里叶幅值谱Fig.11 Fourier amplitude spectra of top accelerations of post 1 and post 2 with the artificial wave

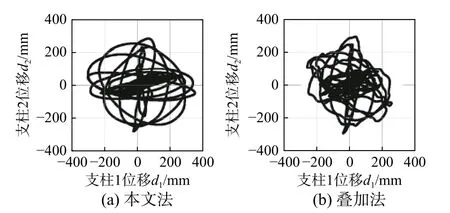
图 12 人工波下支柱1、2 顶部绝对位移散点图Fig.12 Scattering of the absolute top displacement of post 1 and post 2 with the artificial wave

本文解法前提为式(2)右边均为或可近似为位移及其高阶导数的线性组合。弱耦联体系支柱及大部分连接件在地震下均可视为线性构件，故满足该条件。但仍有一部分非线性连接件，如软导线连接，不能直接采用本文解法。尤其对于分裂软导线，在动力作用下的变形可使其刚度可发生明显变化[20]，另外导线初始位型或者两端的非等张拉连接对动刚度特性也会产生显著影响。但注意到，本文解法不依托整体结构矩阵，连接件潜在的非线性也被局部化在其隔离体控制方程中，避免了非线性的扩散。因此基于此线性求解框架进一步研究非线性连接件的解法是合理的，这也是后续研究的重点方向。即对不同形式的软导线，寻求式(2)中力-位移控制方程在非线性形式下的等价线性化方法。