两段式三自由度仿鸟扑翼飞行器机构设计与仿真分析

朱名康，朱建阳

(武汉科技大学机器人与智能系统研究院，湖北 武汉，430081)

扑翼飞行器是基于仿生学原理，模仿鸟类或昆虫等飞行生物的飞行方式而设计的一种飞行器。相对于传统的固定翼和旋翼飞行器，扑翼飞行器具有机动性灵活、飞行效率高、能耗低、隐蔽性好等优点。研究显示，扑翼飞行器有着特殊的高升力产生机制，在小尺度、非定常流场和低雷诺数下有出色的飞行能力[1-2]，与固定翼和旋翼飞行器相比更具优势，而且扑翼飞行器在民用和军用领域均有着极大的发展潜力和应用空间[3]。目前，针对扑翼飞行器的研究主要是从扑翼机构设计分析和翼形空气动力学分析两方面进行的，其中扑翼机构的设计尤为关键，这是飞行器能够模仿飞行生物飞行方式的前提。

早期的仿鸟扑翼飞行器大多是把扑翼简化为单自由度上下扑动的刚体模型，如国外有加州理工学院设计的“Microbat”微型扑翼飞行器[4-5]、Mishra等[6]采用曲柄摇杆机构设计的仿鸟扑翼飞行器“Falcon”；国内有南京航空航天大学设计的“翠雀”仿鸟扑翼飞行器[7]、西北工业大学设计的ASN-211仿鸟扑翼飞行器[8]。单段式仿鸟扑翼飞行器的优点是结构简单、稳定可靠，缺点是未考虑鸟类翅膀的折弯变形和扭转动作，气动性能差、飞行效率低等。

近年来，随着研究的深入，人们发现多段式及多自由度的柔性扑翼有着更好的气动性能，更能模仿鸟类的飞行特征[9-10]。于是国内外研究者设计了大量的多段式仿鸟扑翼飞行器，如Festo公司的仿海鸥扑翼飞行器“SmartBird”[11]采用两段折叠翼设计，外翼可主动扭转，飞行能力极强，但其采用的是混合动力和多驱动，结构复杂；黄鸣阳等[12]设计的多段柔性变体扑翼飞行器以及姜洪利[13]设计的两段式扑翼飞行器等，均采用内翼的“平行四边连杆结构”实现两段翼折叠，外翼则通过惯性或舵机实现扭转，虽然在很大程度上实现了多自由度扑翼，但外翼的扭转设计经常失效，仍有待改进。

为解决上述问题，设计出结构更简单、气动性能更好的多自由度扑翼飞行器，本文在上述研究的基础上，将平行四连杆机构和齿轮齿条运动机构相结合，提出一种新型仿鸟扑翼飞行器扑动机构，即可以仅用一个驱动实现扑翼的扑动、折叠和扭转三个自由度的运动。

1 扑翼机构设计与分析

1.1 扑翼机构设计

海鸥等中大型鸟类飞行过程中，翅膀运动一个周期可划分为4个阶段：下扑阶段、折弯阶段、上提阶段和展开阶段[14]。图1所示为海鸥匀速飞行时翅膀姿态的周期变化，对比翅膀前缘位置变化，可以观察到海鸥翅膀的运动规律。

图1 海鸥匀速飞行时翅膀姿态的周期变化

本研究中，将鸟类翅膀飞行动作简化为扑动、折叠和扭转三个自由度的运动，具体为：以内翼根部弦线为轴心的上下扑动，以内翼和外翼连接处弦线为轴心的折弯变形以及外翼绕展向的扭转。

为使扑翼飞行器更符合图1中鸟类的飞行特征，本文提出扑翼机构的设计要求如下：①两段式扑翼设计；②仅用一个驱动实现扑翼扑动、折叠和扭转三个自由度的运动；③内翼下扑时，外翼展开跟随下扑，同时外翼扭转使前缘向下；④内翼下扑到下极限位置时，外翼折弯一定角度，即折叠角变小；⑤内翼上扑时，外翼维持折叠至上极限位置，同时外翼扭转使前缘向上。

为实现上述设计要求，本文将平行四连杆机构和齿轮齿条运动机构相结合，所设计的新型两段式三自由度扑翼飞行器的扑翼机构三维模型和机构简图如图2所示。由于左右扑翼机构完全对称，下文仅对一侧机构进行理论分析。

图2(b)中，O点为原动件AB与机架的铰接点，∠AOB=90°，杆BC与杆CDE通过滑块在C点连接，内翼段AG通过一个可以绕H点旋转的滑块连接在机架上，DEFG为平行四边形结构，外翼的左端与齿轮J固定，并且齿轮J与齿条DG啮合，外翼还通过旋转副I与连杆EF垂直连接。当主动件AB绕O点旋转时，内翼段与曲柄形成霍肯连杆(Hoeckens linkage)[15]机构而绕H点上下扑动，DEFG平行四边形结构在杆CD的作用下产生运动，随着∠EDG大小的改变，外翼与内翼产生折叠，同时，由于DEFG平行四边形结构的运动，齿轮J与齿条DG产生相对位移，并且齿轮J的旋转带动外翼产生扭转。

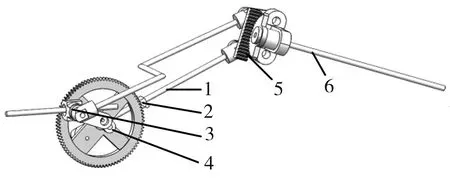
1—内翼;2—旋转滑块;3—移动滑块;4—曲柄;5—齿轮齿条;6—外翼

1.2 扑翼机构分析

设定l0=|AO|,l1=|OB|,l2=|BC|,l3=|CD|,l4=|DE|,l5=|EF|,l6=|AG|,在x-y坐标平面内，C点与x轴的距离为l7，H点与x轴距离为l8，H点与y轴距离为l9。

1.2.1 内翼机构设计分析

设定OB与x轴负半轴重合，OA与y轴负半轴重合时为初始位置。分析该机构可知，当曲柄OA与导杆AG垂直且A点位于H点下方时，内翼到达上扑极限位置，此时内翼上扑角为βu，如图3所示；当曲柄OA与导杆AG垂直且A点位于H点上方时，内翼到达下扑极限位置，此时内翼下扑角为βd，如图4所示。

根据图3中的几何关系，分析可得此时内翼最大上扑动角βu满足以下关系式：

图3 内翼上扑极限位置

(1)

βu=α1

(2)

根据图4中的几何关系，分析可得此时内翼最大下扑动角βd满足以下关系式：

图4 内翼下扑极限位置

(3)

βd=π-α2

(4)

由此可得内翼扑动角幅值为：β=βu+βd。类比中大型鸟类的飞行姿态，取β=50°，βu=40°，βd=10°。考虑样机尺寸和加工难度，取曲柄OA的长度l0=12 mm。将这些数据代入到式(1)～式(4)中，得到一个二元一次方程，解此方程可以得到l8=7.4 mm，l9=27.4 mm，即H点坐标为(27.4，7.4)。

设计样机翼展为1000 mm，机身宽度为120 mm，故单边翼展为440 mm；外翼与内翼长度比值约为1.55[16]，故内翼长度为172 mm，外翼长度为268 mm；由于内翼的HG段才能算作内翼部分，而|OH|=28.4 mm，综合考虑，取内翼AG的长度l6=202 mm。

1.2.2 外翼机构设计分析

(5)

γ1=∠GDM=∠CDG-∠CDM

(6)

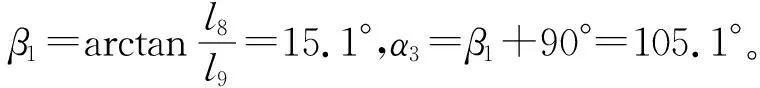
(7)

γ2=∠GDM=∠CDM-∠CDG

(8)

式中：β2=β1，α4=β2+270°=285.1°。

此外，图5和图6所示位置的机构还满足以下关系：

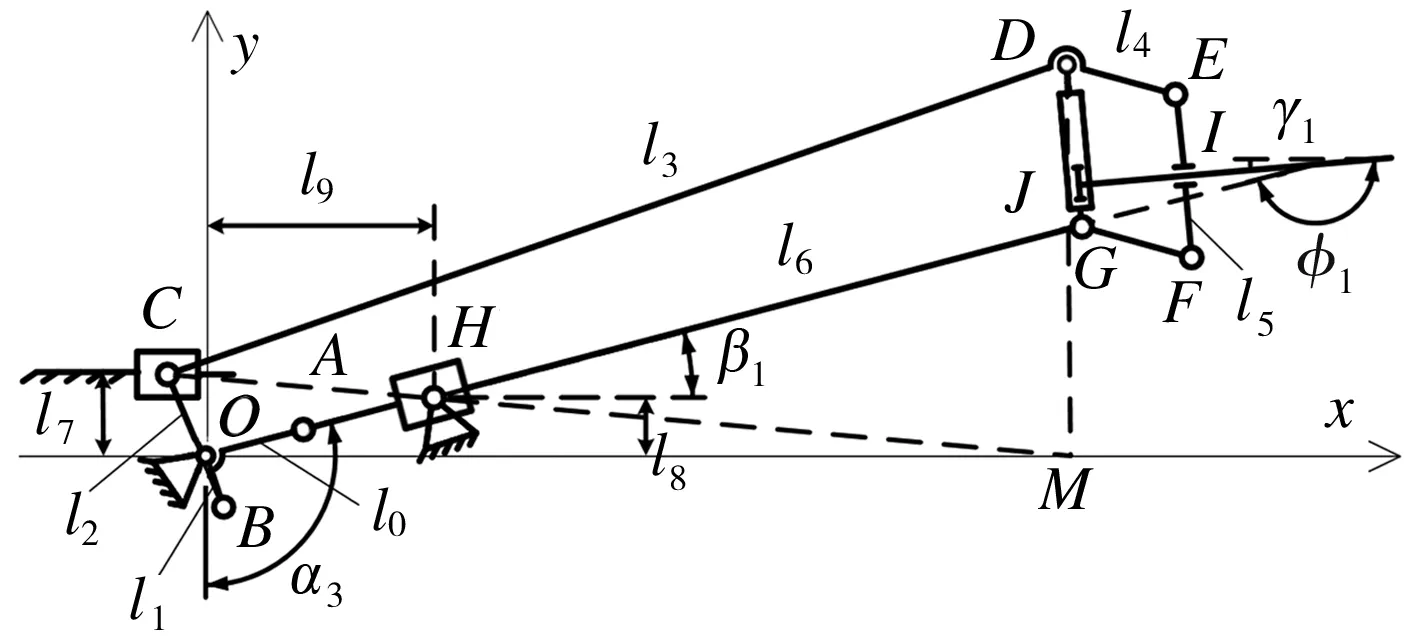
图5 折叠角最大对应的位置

图6 折叠角最小对应的位置

(9)

(10)

根据上述数据重新绘制机构简图，分析可知，扭转角λ主要与l4和∠EDG的大小有关，而∠CDE为定值，∠CDG越大，∠EDG越小，齿轮J向G点方向的位移越大，因此在内翼下扑过程中，当连杆OB与连杆BC重合时，扭转角最大且外翼前缘向下，如图7所示。图7中的扭转角λ满足以下关系式：

图7 扭转角最大对应的位置

(11)

∠EDG=∠CDE-∠CDG

(12)

取扭转角为±20°，齿轮J模数m为0.6，齿数z为44，则齿轮分度圆直径d=mz=26.4 mm，计算得到此时lJ=4.6 mm，取l4=14 mm，λ=20°，则∠EDG=70.8°，计算得到∠CDG=79.7°，故∠CDE=150.5°。

同理可得，在上扑过程中，当∠EDG=π-70.8°=109.2°时，齿轮J向D点方向的位移最大，此时扭转角最小为-20°，且外翼前缘向上，如图8所示。

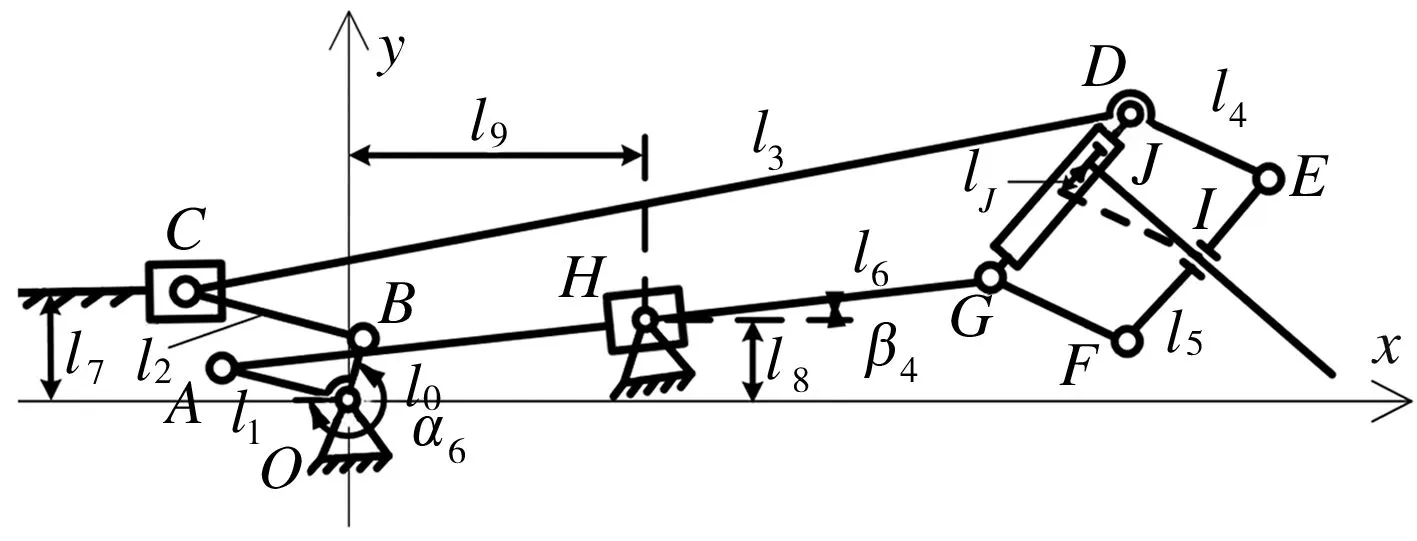
图8 扭转角最小对应的位置

利用以上得出的所有杆长参数进行建模仿真，处理后得到在一个周期内曲柄OA、内翼段AG以及外翼段的轨迹图如图9所示。仿真结果表明，机构的运动轨迹符合设计要求，最终确定扑翼机构的设计参数列于表1和表2中。

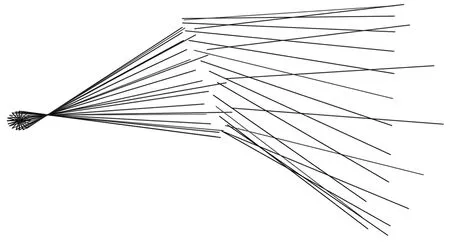
图9 曲柄、内翼及外翼段一个周期内的轨迹图

表1 扑翼机构尺寸参数表

表2 扑翼机构角度参数

2 新型扑翼机构仿真分析

根据上述确定的扑翼机构参数，利用SolidWorks软件进行建模并导入ADAMS软件中，添加运动副，对机构进行仿真分析后得到“香蕉”形翼尖轨迹，如图10所示。

图10 扑翼机构仿真和翼尖轨迹

利用ADAMS软件的Angle Measure工具对机构的内翼扑动角、内外翼折叠角和外翼扭转角进行测量，设定曲柄驱动角速度为1440 rad/s(扑动频率为4 Hz)，处理得到各角随时间的变化曲线如图11所示，仿真得到内翼扑动角范围为-9.9°～40.1°，内外翼之间的折叠角范围为132.3°～173.5°，外翼扭转角范围为-19.6°～19.9°。由图11可知，这三个角度随时间的变化曲线均保持完整的周期性，在内翼下扑过程中，折叠角逐渐增至最大值，并且外翼前缘向下扭转；内翼上扑过程中，折叠角逐渐减小至最小值，且外翼前缘向下扭转。该仿真结果与上述机构设计得到的结果相一致，均满足设计要求，该设计的有效性和准确性得到验证。

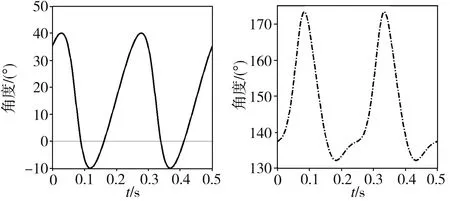
(a)内翼扑动角 (b)内外翼之间折叠角

3 扑翼飞行器气动力计算

研究表明，使用数值计算方法可以快速准确地计算扑翼的气动力[17-18]。基于此，本文采用基于准定常气动力计算模型的方法计算所设计扑翼飞行器的升力和推力[19]。

(a)上扑过程 (b)下扑过程

扑翼单位微段在扑动过程中,某时刻产生的气动力满足如下关系式：

(13)

(14)

F′L=F′ScosαV+F′DsinαV

(15)

F′T=F′SsinαV-F′DcosαV

(16)

式中：ρ为空气密度，CL和CD为微段的升力系数和阻力系数。

利用Profili软件计算NACA 6409翼型在不同迎角下的升阻力系数并进行拟合，得到数据如图13所示。由图13可知，在迎角为11°左右时,微段翼型达到最高升阻力系数比。

(a)升力和阻力系数 (b)升阻比

对F′L和F′T沿展长b进行积分，可得到单个扑翼一个周期内的升力FL和推力FT，即：

(17)

(18)

设定平飞速度V∞=5 m/s、安装角α0=5°，把所得参数代入式(17)和式(18)中，得到一个周期内扑翼的升力和推力大小以及扑翼在只有扑动而没有折叠和扭转的单自由度运动情况下的升力和推力，如图14所示。由图14可见，三自由度扑翼在一个周期内的升力先增大后减小，最大升力为360 g，平均升力为211 g；其推力则先增大后减小再增大，呈正弦波变化趋势，最大推力为4.5 g，平均推力为1.2 g，平均推力接近于0，表明理论上扑翼飞行器可以在5 m/s速度下匀速飞行；相较于单自由度扑翼，三自由度扑翼升力和推力均有明显提高，平均升力提升了68.5%，平均推力提升了150%。

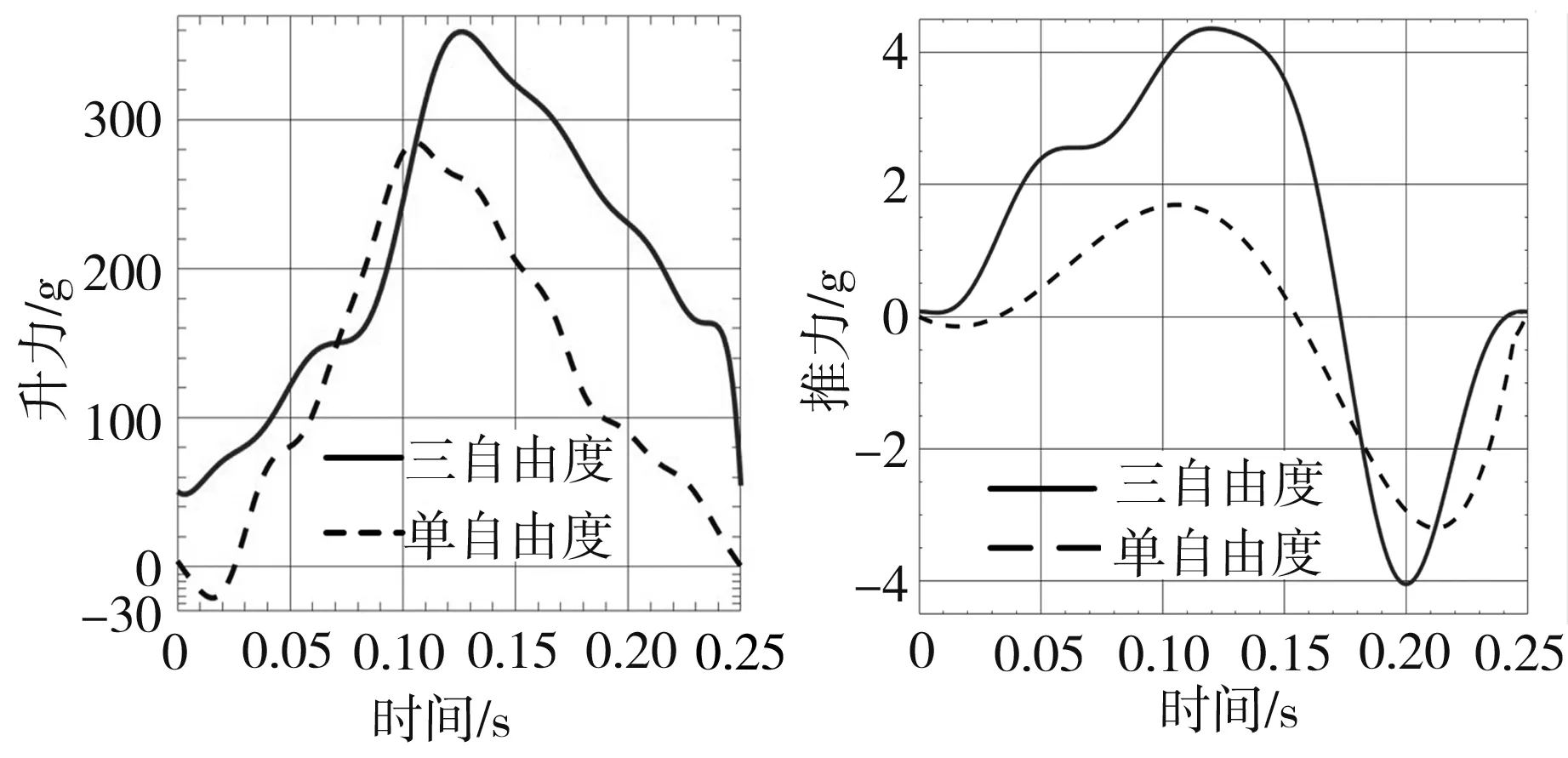
(a)升力FL (b)推力FT

4 扑翼飞行器样机制作

使用SolidWorks软件对该两段式三自由度扑翼飞行器完成整体设计和三维建模，并根据三维模型制作出样机，如图15所示。

(a)扑翼飞行器三维模型

样机采用一个Kv值为1500的无刷电机进行驱动，由7.4 V锂电池供电，当使用最大电流为12 A的电子调速器时，无刷电机最高空载转速为11 100 r/min，最大功率为88.8 W，通过齿轮组减速，由电子调速器调节无刷电机的电压和电流大小，从而控制扑翼机构的扑动频率在0～8 Hz范围。内翼和外翼的主支架上均匀地固定有翼型骨架，且骨架上蒙附一层薄膜制作的翅膀。采用扇形平面尾翼设计，通过两个垂直布置的舵机控制方向，实现调节飞行姿态的作用。通过微型无线接收机接收地面遥控装置的信号来控制飞行器的运转。为减少重量，机身骨架和零件使用炭纤维材料加工而成，机身翼展1000 mm，重190 g。根据鸟类扑翼飞行仿生学尺度律[20]，样机参数符合设计标准。

样机在一个周期内的扑动姿态变化如图16所示。分析图16可知，画面1～5为下扑阶段，此时外翼前缘向下扭转，画面3中外翼伸展至折叠角最大，可以增大翅膀受力面积以增大升力，随后外翼继续下扑；画面6～10为上扑阶段，此时外翼前缘向上扭转，内外翼保持折叠至最高位置，可减小翅膀受力面积以减小阻力；画面11～12为下扑阶段，衔接画面1～2开始下一周期。整个扑动过程符合鸟类飞行特征。样机飞行试验中，机构运行平顺，稳定可靠，进一步验证了该机构设计的合理性。

图16 样机一个周期内的扑动姿态

5 结语

本文将平行四连杆机构和齿轮齿条运动机构相结合，设计了一种新型仿鸟扑翼飞行器扑动机构，即仅用一个驱动实现扑翼的扑动、折叠和扭转三个自由度的运动。通过理论计算和参数优化，得到机构的内翼扑动角为-9.9°～40.1°，内外翼之间的折叠角为132.3°～173.5°，外翼扭转角为-19.6°～19.9°，符合设计要求。仿真结果显示，扑翼机构内翼下扑时，外翼展开，同时外翼扭转使前缘向下；内翼下扑时，外翼折叠，同时外翼扭转使前缘向上。扑翼的扑动、折叠和扭转三个自由度的配合过程符合鸟类飞行特征，扑翼飞行器的飞行效率更高，气动性能更强，仿生性较好。另外，所设计机构的翼尖轨迹为“香蕉”形，下扑过程的翼面积大于上扑过程的翼面积，可在减小阻力的同时，有效提高飞行过程中的升力和推力。