广义圆锥倒角V型柔性铰链设计与分析
2021-04-21孔建益鲜小东王郢瑞于普良
黄 朝,孔建益,鲜小东,王郢瑞,于普良
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.武汉科技大学省部共建耐火材料与冶金国家重点实验室,湖北 武汉,430081)
柔性铰链具有体积小、无间隙、无摩擦、灵敏度高、运动平稳等优点[1-3],已越来越多地应用于各种超精密运动装备中,如微纳米驱动平台、高精度校准装置和压电驱动器的位移放大器[4-6]。柔性机构的整体性能在一定程度上依赖于柔性铰链的固有特性,因此,如何选择和设计柔性铰链具有重要的研究意义。
Paros等[7]研究了圆弧柔性铰链,并推导出完整的柔度计算公式。Zettl等[8]建立了直圆柔性铰链的有限元模型,完善了柔性铰链的有限元分析方法。Smith等[9]推导出椭圆型柔性铰链的柔度方程,拓展了柔性铰链的研究领域。Chen等[10]通过改变椭圆最大偏心角设计出一种椭圆弧型柔性铰链,基于卡氏第二定理推导了该类铰链的柔度方程。Lobontiu等[11]引入两种新型结构,即抛物线型和双曲线型柔性铰链,并推导了相应的解析方程,证明双曲线型柔性铰链比直圆型、椭圆型及抛物线型柔性铰链具有更高的精度。Wang等[12]设计了一种非对称的指数正弦型柔性铰链,通过理论分析证明此类柔性铰链相较于对称型柔性铰链有更高的运动精度。Li等[13]给出幂函数型柔性铰链的柔度方程,对其运动精度进行了分析,结果表明幂函数型柔性铰链比正圆型和V型柔性铰链具有更高的旋转精度。
在柔性铰链设计过程中,一般需要同时兼顾其结构类型和结构参数。设计者往往首先根据经验来选择结构类型,然后再根据铰链的柔度方程来设计结构参数。由于每种柔性铰链的柔度方程都是独特的,所以在柔性铰链选型和设计时,设计者必须针对不同类型分别进行计算,致使找到最适合的柔性铰链来实现机构最佳性能的难度增加,因此有必要建立一个适用于多种类型柔性铰链的广义模型。
本文提出一种新型的广义柔性铰链模型——圆锥倒角V型柔性铰链,具体包括抛物线倒角V型、椭圆倒角V型、双曲线倒角V型、抛物线型、椭圆弧型、双曲线型及直梁型柔性铰链,并以极坐标下的圆锥曲线广义方程为基础,推导了圆锥倒角V型柔性铰链的柔度广义方程,运用这些方程可以同时进行切口类型选择和参数设计,从而优化柔性铰链的设计过程。
1 极坐标下圆锥曲线的广义方程
如图1所示,圆锥倒角V型柔性铰链的切口轮廓由圆锥曲线及其切线构成,其几何参数包括切口长度l、切口部分最小厚度t、宽度w以及切线部分与x轴之间的夹角φ。
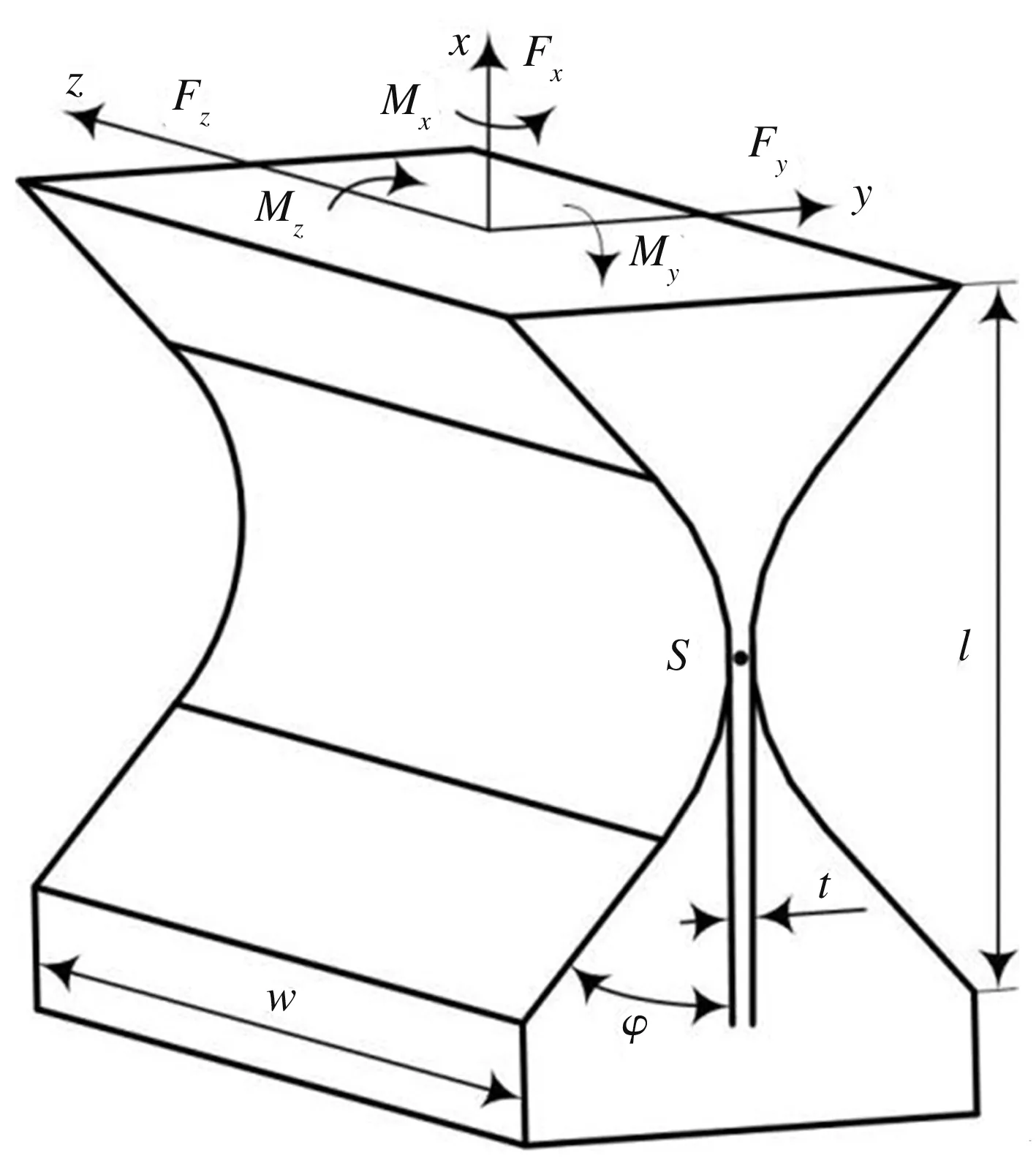
图1 圆锥倒角V型柔性铰链简图
图2所示为圆锥曲线及其准线和焦点OF,在极坐标系中,以焦点OF为原点,圆锥曲线可表示为:
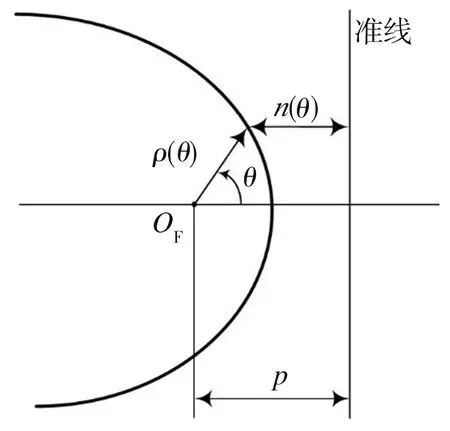
图2 极坐标系中的圆锥曲线
(1)
式中:p(p>0)表示焦点与准线之间的距离;离心率e(e>0)可表示为:
(2)
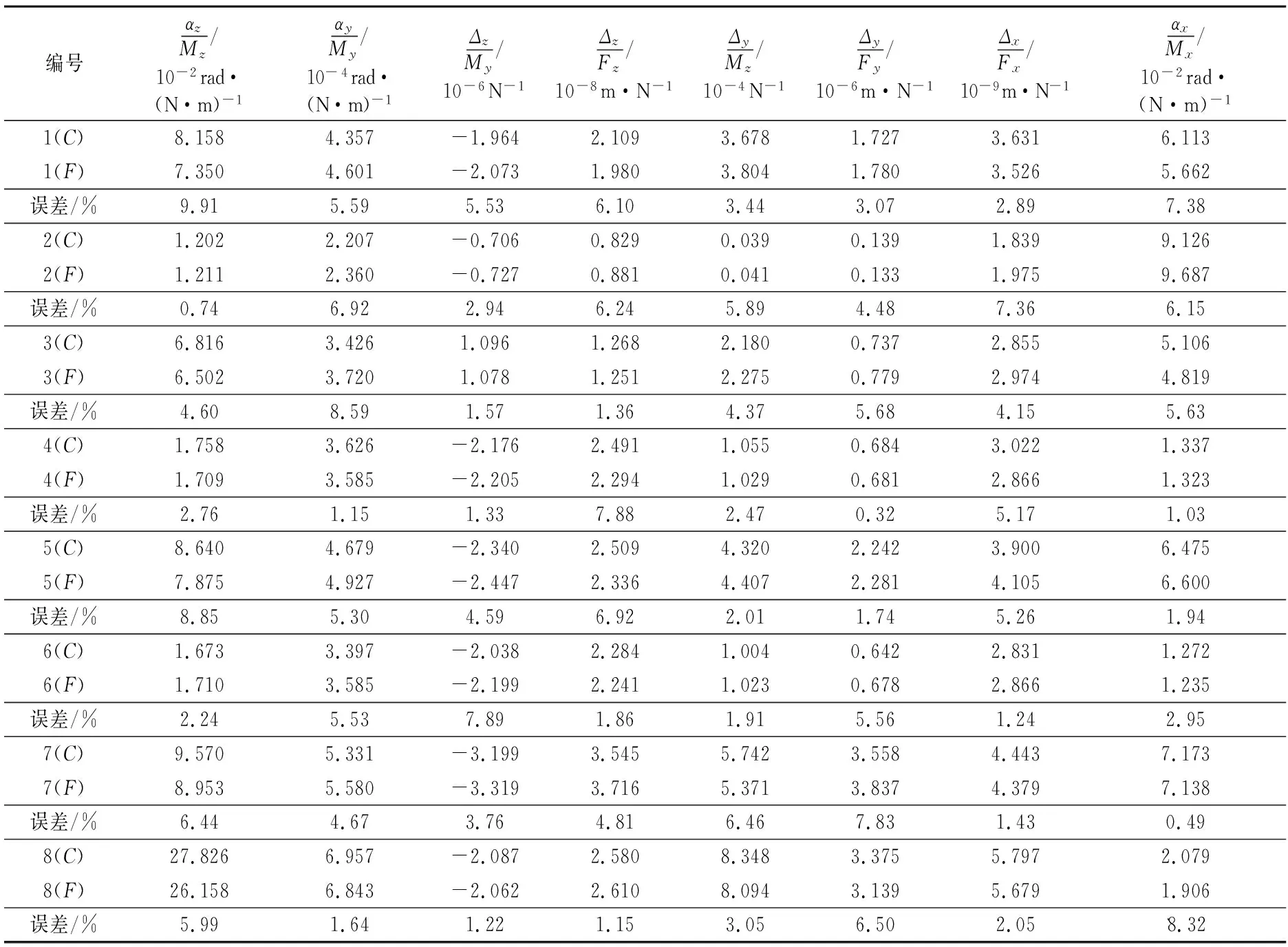
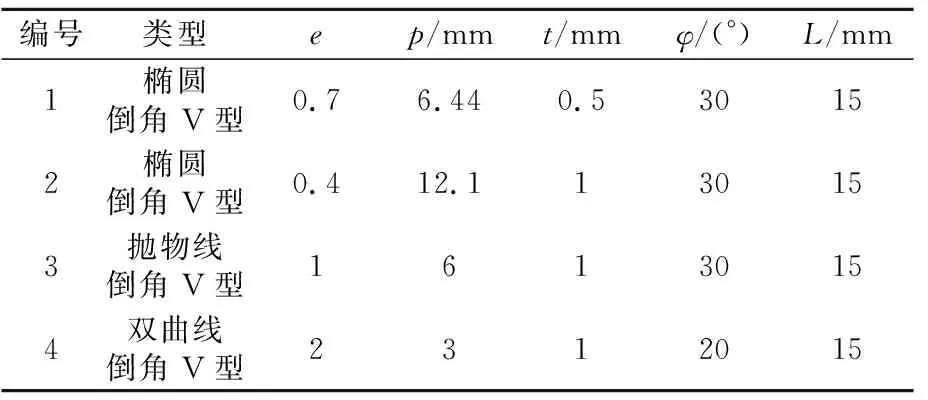
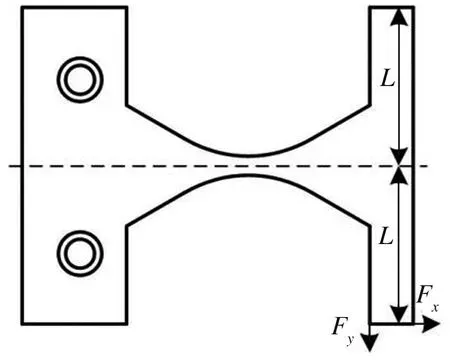
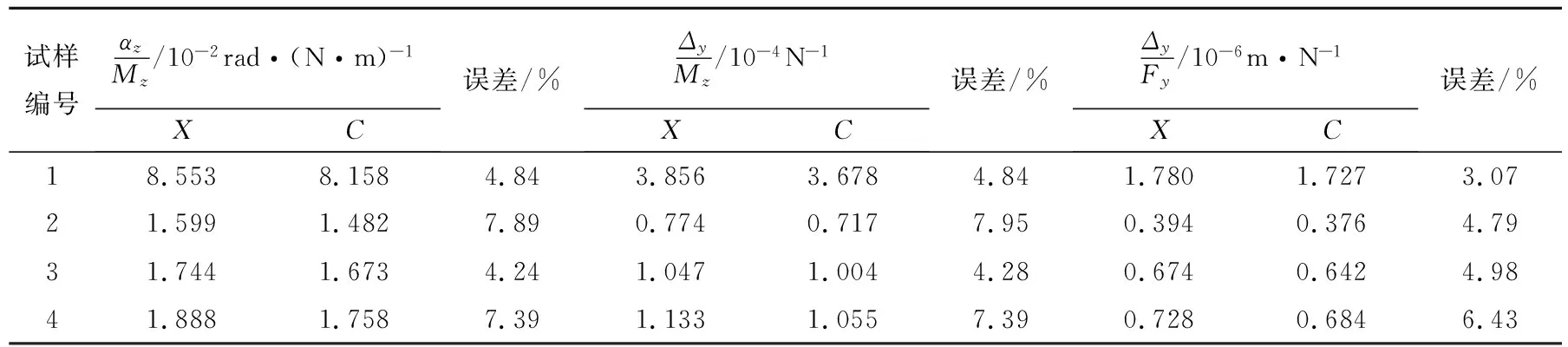
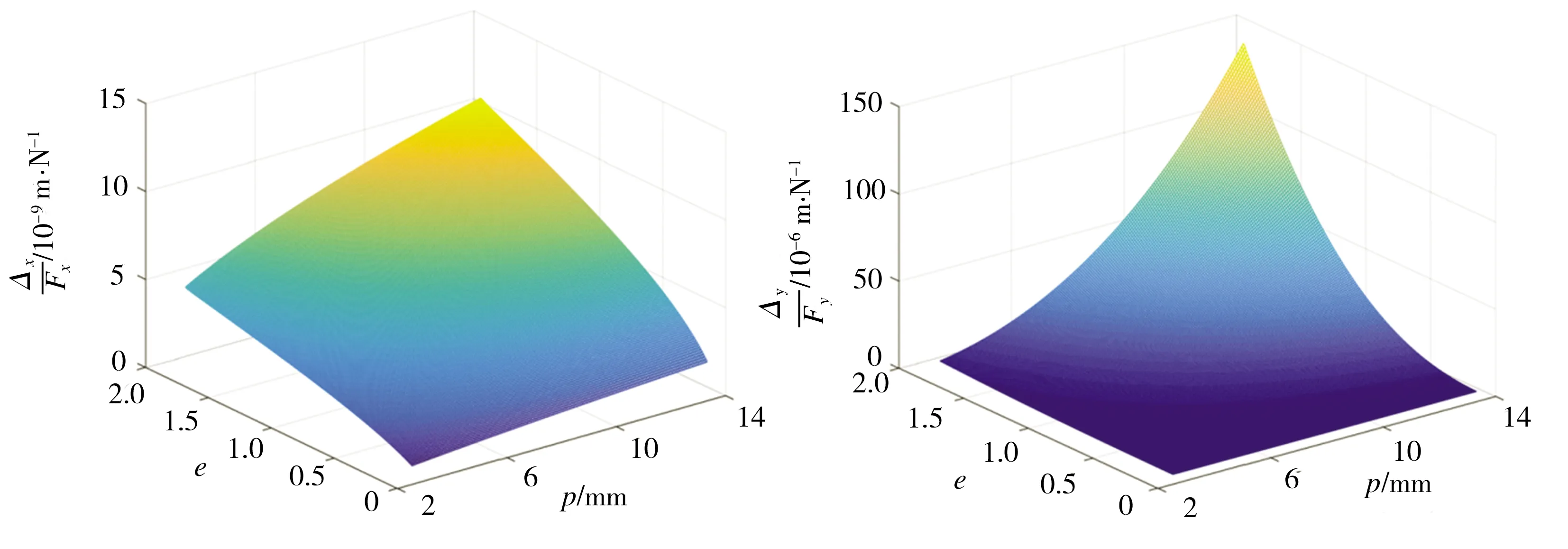
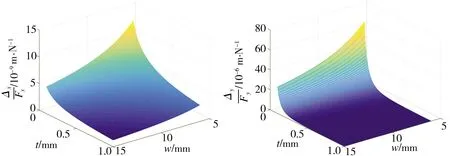
当e>1时,圆锥曲线表示的是双曲线;当e=1时,圆锥曲线表示的是抛物线;当0 如图3所示,切口对应到圆锥曲线的范围设定为[-θn,θn],其中θn=π/2,圆锥曲线部分范围为[-θm,θm],θm为圆锥曲线部分最大极角,切线部分可表示为: 图3 圆锥倒角V型柔性铰链的截面图 (3) 其中, (4) 切口长度l的计算公式为: (5) 图4所示为具有不同切口曲线的圆锥倒角V型柔性铰链之间的关系,对应于不同范围的e和φ,可得到不同类型的柔性铰链。在圆锥倒角V型柔性铰链广义模型中,e>0、0≤φ≤φm、0≤θm≤θn,φm的计算公式为: 图4 不同切口轮廓的圆锥倒角V型柔性铰链之间的关系 (6) 当φ=0时,模型代表直梁型柔性铰链;当0<φ<φm时,根据不同的e值,模型分别代表椭圆倒角V型、抛物线倒角V型和双曲线倒角V型柔性铰链;当φ=φm时,根据不同的e值,模型分别代表椭圆弧型、抛物线型和双曲线型柔性铰链。 如图3所示,将柔性铰链切口部分垂直地划分为无数块长方体,dθ(dθ→0)所对应的长方体的高度可表示为: (7) 其中, (8) (9) x与θ的关系可表示为: (10) 对上式求导可得: (11) 当柔性铰链切口处最小厚度t远小于切口长度l(t<0.2l)时,可将柔性铰链视为一端固定且受弯矩、轴向载荷、剪切和扭转作用的悬臂梁[14],作用在铰链上的载荷力(参见图1)可定义为: (12) 铰链相应的变形为: (13) 由卡氏第二定理可得: X=ChF (14) 式中:Ch为柔度矩阵,可表示为 Ch= (15) 鉴于柔度矩阵的对称性,有αz/Fy=Δy/Mz、αy/Fz=Δz/My,柔度矩阵中的每一个柔度因子都可以由欧拉-伯努利梁理论推导而出。 z轴是柔性铰链的输入轴,弯矩Mz对应的关于z轴的角柔度可表示为: 在太原市平阳路君怡小区B座钢筋混凝土不等肢剪力墙结构中,结构的位移超过了规范规定的限值,设计人员通过合理地调整墙肢截面或连梁的截面高度来提高整体的刚度,从而满足了规范规定的位移限值。对于设计中跨高比较大的连梁,有良好的地震耗能。而在剪力墙结构中,往往洞口上形成的连梁跨高比均比较小,对抗震等级为一、二级且连梁跨高比≯2、墙肢厚≮200 mm时,可设置斜向交叉钢筋或菱形斜筋与交叉斜筋组合的配筋方案,其延性均比较高,且具有良好的耗能能力。当连梁宽度在350 mm以上时,可采用交叉暗撑。对在工程中出现超筋的连梁,通过合理配筋保证梁强剪弱弯,可具备一定的延性耗能能力。 (16) 式中:E为材料的弹性模量;Iz(θ)为角θ处梁截面相对于中性轴的转动惯量;I1的计算公式为 (17) 通过施加力Fy,产生的等效力矩为Fy[l/2-epsinθ/(1+ecosθ)],因此力Fy对应的角柔度为 (18) 弯矩My对应的关于y轴的角柔度为: (19) 其中, (20) 通过施加力Fz,产生的等效力矩为-Fz[l/2-epsinθ/(1+ecosθ)],因此力Fz对应的角柔度为 (21) 由于柔度矩阵的对称性,弯矩My对应的关于z轴的线柔度为: (22) (23) 式中:G为材料的剪切模量;k为材料的剪切系数,对于截面为矩形的梁,k取6/5[15]。 弯曲部分计算公式为: (24) 综上,力Fz沿z轴的线柔度为: (25) 其中, (26) 同理,由于柔度矩阵的对称性,弯矩Mz对应的沿y轴的线柔度为: (27) 参照对Δz/Fz的推导,也可得出力Fy对应的沿y轴的线柔度为: (28) 其中, (29) 沿x轴方向的线柔度可表示为: (30) 由于柔性铰链的每一个无穷小矩形条都可以看作是一个恒定的矩形截面梁,根据文献[16]中给出的近似扭转方程,关于x轴的角柔度可以表示为: (31) 为了验证所提出的柔度方程的正确性,下面采用有限元分析方法来计算柔性铰链的各个柔度因子。首先通过Solidworks软件建立铰链三维模型如图5所示。用HyperMesh软件划分网格单元,选取Solid186单元类型,Solid186是一个高阶三维20节点固体结构单元,具有任意的空间各向异性。然后建立质量点,设置为Mass21单元,创建MPC约束。最后在有限元分析软件中进行计算,对于每一类柔性铰链,均在其一端固定而在另一端施加单位载荷,计算得到的位移就是相应的柔度因子。 图5 有限元模型 表1列出了8组圆锥倒角V型柔性铰链的几何参数,柔性铰链的宽度w均为10 mm,材质为弹簧钢,其杨氏模量E为207 GPa,剪切模量G为81 GPa。 表1 圆锥倒角V型柔性铰链仿真模型的参数 表2列出了上述柔性铰链模型的柔度因子的理论计算值(用C表示)和有限元分析结果(用F表示),并给出了两者之间的相对误差(|F-C|/|C|)。鉴于柔度矩阵的对称性,表2中只给出αz/Mz、αy/My、Δz/My、Δz/Fz、Δy/Mz、Δy/Fy、Δx/Fx和αx/Mx的值。由表2可见,这些柔度因子的理论计算值和有限元分析结果的误差均在10%以内,具有较好的一致性。 表2 柔度因子的理论计算值(用C表示)与有限元分析结果(用F表示)的比较 选取3个柔度因子αz/Mz、Δy/Mz和Δy/Fy,通过实验对所提出的柔度方程进行验证。加工了4个柔性铰链,其设计参数如表3所示。每个柔性铰链均被加工成类似于“I”形,如图6所示。铰链材料选用弹簧钢65Mn,采用慢走丝电火花线切割技术进行加工。 表3 圆锥倒角V型柔性铰链试样参数 图6 柔性铰链试样简图 图7所示为实验平台,包括激光位移传感器(型号为KEYENCE®LK-G155H,分辨率为0.5μm)、光学平板、支撑杆、变压器、砝码(从10 g到500 g)以及柔性铰链试样。两根支撑杆固定在光学平板上,感测头和柔性铰链试样分别由光轴连接件固定于支撑杆上,柔性铰链试样一端固定,另一端通过砝码施加载荷。如图7(a)所示,施加力Fx以产生力矩Mz=FxL,测量得到相应的位移即可计算出柔度因子Δy/Mz,由于变形量足够小,所以角位移αz≈tanαz,可计算出柔度因子αz/Mz[17]。如图7(b)所示,可测量出在力Fy作用下的位移,计算出柔度因子Δy/Fy。表4中列出了理论计算值(用C表示)与实验值(用X表示)的对比,相对误差(|X-C|/|C|)均在8%以内。 表4 柔度因子的实验结果(用X表示)与理论计算值(用C表示)的比较 图7 实验设备:(a)用于计算αz/Mz和Δy/Mz;(b)用于计算Δy/Fy 柔性铰链的实验误差主要来自以下几个潜在因素:(1)加工的不确定性,加工样品与设计样品之间存在一定误差;(2)测量系统的不确定性,由于测量系统所造成的误差;(3)所施加载荷的不确定性,施加载荷由砝码质量所决定,砝码质量真实值与其标定值可能存在误差。 由于柔性铰链的平面运动(绕z轴的旋转、沿x轴的平动和沿y轴的平动)在实际工况中占主导地位,因此本文采用数值模拟分析方法,基于解析模型研究柔性铰链尺寸参数对铰链平面柔度的影响。 在圆锥倒角V型柔性铰链的广义模型中,e、p、t、w和φ为设计参数,柔性铰链的切口曲线由e、p和φ共同确定,柔性铰链的结构特征则由t和w共同确定。 为了研究切口曲线对铰链柔度的影响:首先将t、w和φ分别设为0.5 mm、10 mm和π/6,将e和p的取值范围分别设为0.1~1.9和3~13 mm,得到图8所示的铰链平面柔度与e、p之间的关系;然后将e、p、t和w分别设为0.6、5.33 mm、0.5 mm和10 mm,将φ的取值范围设为0~5π/18,得到图9所示的铰链平面柔度与φ之间的关系。为了研究结构特征对铰链柔度的影响,将e、p和φ分别设为0.6、5.33 mm和π/6,将t和w的取值范围分别设为0.1~1 mm和6~15 mm,得到图10所示的铰链平面柔度与t和w之间的关系。 由图8可见,4个柔度因子均随e和p的增大而非线性增加。其中,Δx/Fx和αz/Mz的增长率随着e和p的增大而逐渐降低,而Δy/Fy和Δy/Mz的增长率随着e和p的增大而逐渐提高。 (a)Δx/Fx (b)Δy/Fy 由图9可见,4个柔度因子均随φ的增加而非线性减少,而且柔度因子的变化率随着φ的增大而逐渐降低,最终趋于稳定。当数值不再变化时,即得到传统圆锥曲线型柔性铰链的柔度值,这表明在设计参数e、p、t和w相同的情况下,圆锥倒角V型柔性铰链的柔度大于传统的圆锥曲线型柔性铰链的柔度。 (a)Δx/Fx (b)Δy/Fy 由图10可见,4个柔度因子均随t和w的增大而非线性减少,而且柔度因子的变化率随着t和w的增加而逐渐降低,其中,对于Δy/Fy、Δy/Mz和αz/Mz的变化,t比w的影响程度更大。 (a)Δx/Fx (b)Δy/Fy 本文设计了一种新型的广义柔性铰链,即圆锥倒角V型柔性铰链,包含抛物线倒角V型、椭圆倒角V型、双曲线倒角V型、抛物线型、椭圆弧型、双曲线型及直梁型柔性铰链。通过对设计参数e、p、t、w和φ的设定,可同时实现此类柔性铰链结构类型和结构参数的综合设计。 然后推导了圆锥倒角V型柔性铰链的柔度方程,并进行了有限元分析和实验研究。理论计算值与有限元分析结果的误差在10%以内,与实验结果的误差在8%以内,证明了柔度方程的正确性和有效性。 最后基于柔度方程分析了设计参数e、p、t、w和φ对所设计的柔性铰链平面柔度的影响规律。研究表明,柔度因子随着设计参数e和p的增大而增大,随着设计参数φ、t和w的增大而减小;在设计参数e、p、t和w相同的情况下,圆锥倒角V型柔性铰链的柔度大于传统的圆锥曲线型柔性铰链的柔度。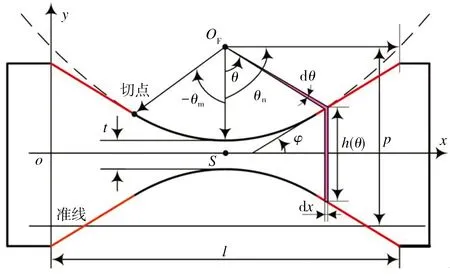
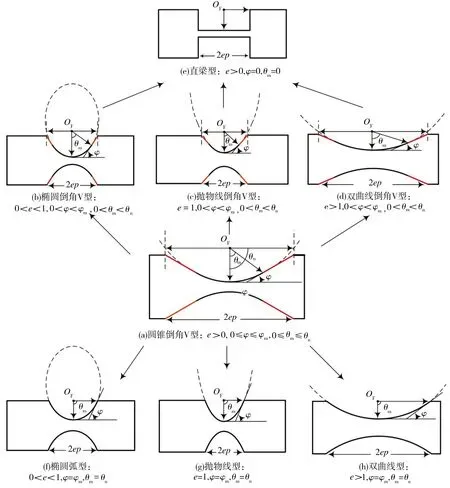
2 圆锥倒角V型柔性铰链的柔度方程
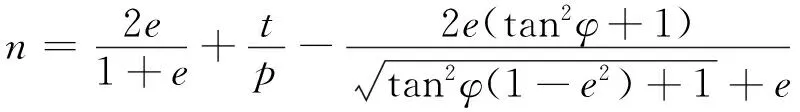
2.1 柔度矩阵
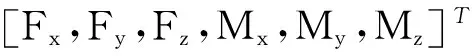

2.2 关于z轴的角柔度
2.3 关于y轴的角柔度
2.4 沿z轴方向的线柔度
2.5 沿y轴方向的线柔度
2.6 沿x轴方向的线柔度
2.7 关于x轴的角柔度
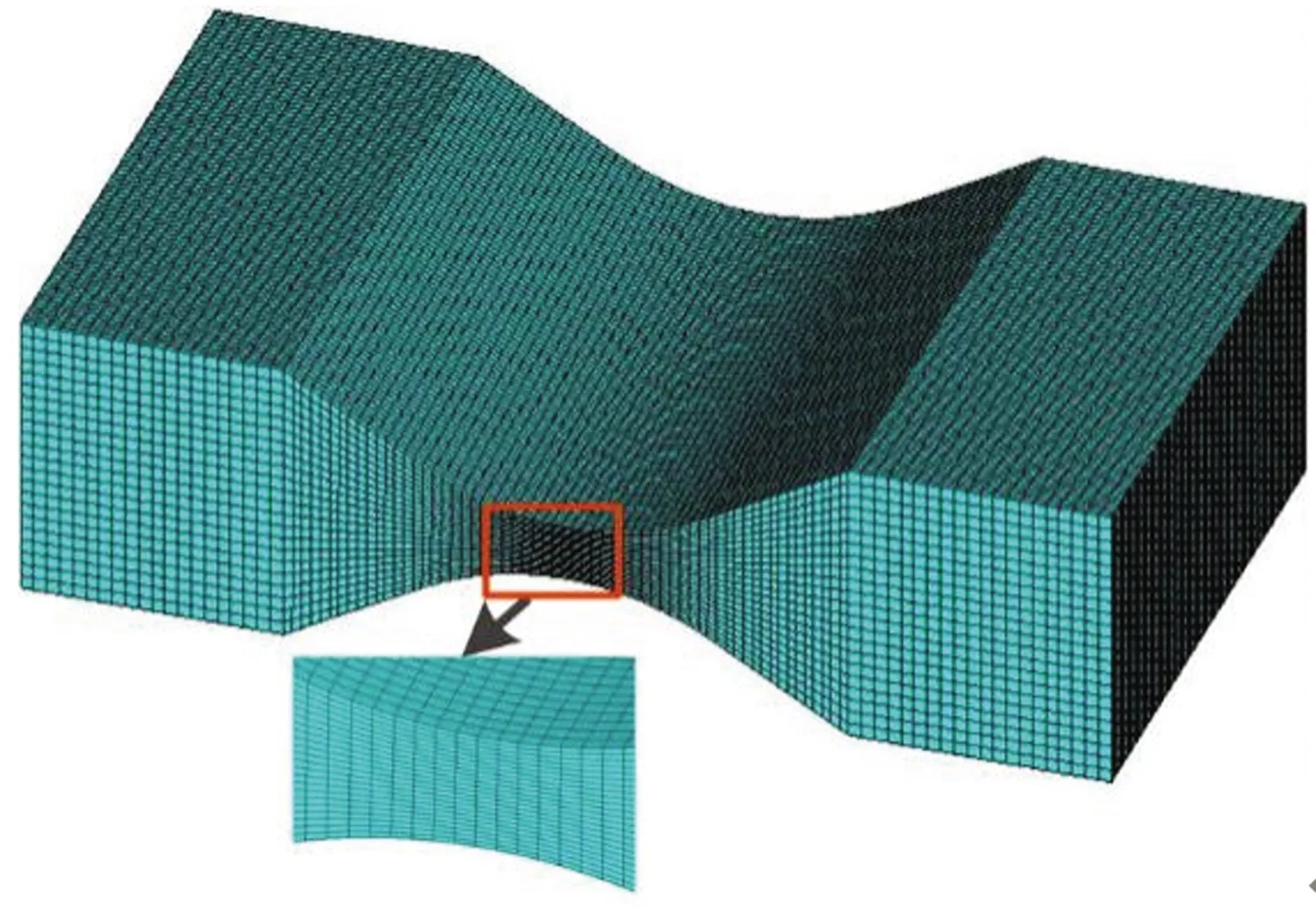
3 有限元分析验证
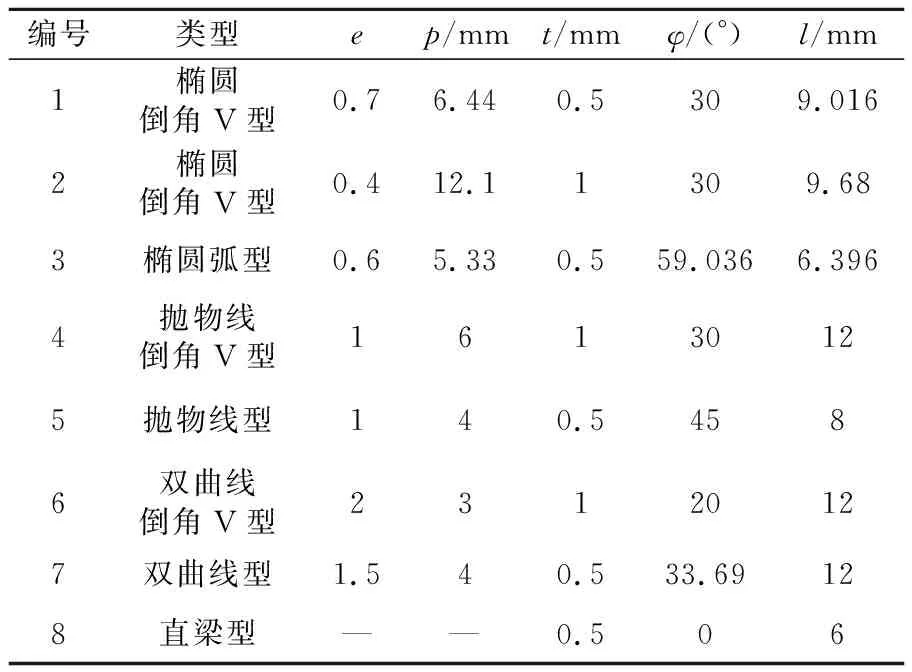
4 实验验证

5 性能分析与比较

6 结语
