基于双层循环的流水车间调度与设备维护鲁棒集成优化方法

高明中，唐秋华，钱新博

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

生产调度和设备维护是相互关联、相互影响的。持续生产一段时间后，机器可靠性会降低，可能发生机器故障，需要中断生产进行维护，使其恢复到工作状态；或在设备发生故障前，根据“预防为主”“防患于未然”的原则，进行有计划的预防性维修。因此，在车间管理时必须综合考虑生产调度、预防维护和故障维护，通过集成优化来降低生产成本、延长设备寿命、提高产品质量。更重要的是，在集成优化过程中需要保证调度方案具有足够的鲁棒性，以促成生产组织与设备维护的无缝衔接。

生产调度与设备维护的集成优化通常分成两类：确定型和不确定型。确定型问题中，通过安排足量的预防维护来保证设备具备较高的可靠性，无需考虑随机故障的发生。此方面研究目前已相对成熟，如Wang等[1]研究了两阶段混合流水车间的生产调度与预防维护集成优化，可同时优化制造周期和第一阶段机器可用性。不确定型问题不仅需要考虑预防维护，更要考虑随时可能发生的机器故障。Cassady等[2]和Cui等[3]以鲁棒性为目标，建立了设备故障函数服从Weibull分布时的单机调度鲁棒集成优化模型。Herroelen等[4]将鲁棒性分为两种：制造周期鲁棒性和开始时间鲁棒性，前者是指在随机故障发生后调度目标变动不大，后者是指在随机故障产生后各操作的实际开始时间调整幅度不大。Xiong等[5]研究了存在随机故障的柔性流水车间鲁棒调度问题，以制造周期鲁棒性和开始时间鲁棒性为优化目标，提出两种鲁棒性指标：一是考虑故障概率，二是考虑故障时间及位置。Paprocka[6]、Sajadi等[7]均研究了鲁棒集成优化问题，指出需在初始调度中插入闲置时间，以提高系统的鲁棒性。Lu等[8]和Cui等[9]以制造周期鲁棒性和开始时间鲁棒性为目标，使用遗传算法优化闲置时间。但是上述文献均是针对小规模案例，未根据所研究问题的特点改进算法。针对大规模生产调度问题的求解，需要制定新的算法，解决目前存在的计算时间长、算法收敛速度慢等问题。

为此，本文提出一种基于双层循环的鲁棒优化算法，实现大规模案例下的置换流水车间生产调度与设备维护集成优化。其中，特别针对插入性闲置时间的优化问题，做出两个改进：①提出基于关键路径的启发式规则，以改善初始解的性能；②在传统灰狼优化算法的基础上融入交叉算子，加强种群之间的信息交流。

1 问题描述及求解思路

本文所研究的问题描述如下：

(1)n个工件顺次经过m道工序，每道工序仅有一台机器，且各工件在每台机器上的加工顺序相同。不考虑工件的加工准备时间及机器的换型时间。

(2)预防维护只会在机器待机时执行，执行预防维护会使机器“恢复如新”，设备役龄清零。

(3)假定所发生故障均可被修复，且故障后立即执行设备维护。因故障而中断的操作可以继续，不会造成额外的时间损失；故障维护采取最小维修规则，设备修复后寿命不变。

(5)以制造周期鲁棒性和开始时间鲁棒性的线性加权值最小化作为优化目标。

在置换流水车间生产调度与设备维护的集成优化时，需要考虑多种生产情形：①正常工作，即置换流水车间内工件能正常加工；②根据设备可用性、可靠性等的预测，在机器待机时决策执行预防性维护；③设备故障后立即维护。当三者集成时，生产过程就变成多种情形间的切换。

针对上述问题，本文提出如图1所示的基于双层循环的鲁棒优化方法。其中，外层循环调整加工序列，确定执行设备预防维护的位置；在此基础上，内层循环优化插入性闲置时间，实现调度方案的鲁棒性。外层循环通过邻域搜索改变初始加工序列，继而改变预防维护位置矩阵；内层循环包含两部分：基于启发式规则的闲置时间初始解生成以及基于改进灰狼算法的闲置时间优化。双层循环不断迭代，直至达到终止条件，得到鲁棒性最优的调度计划。

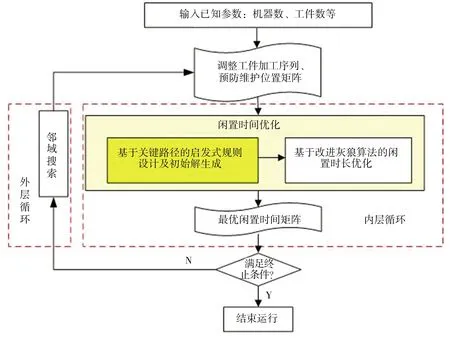
图1 基于双层循环的车间调度、预防维护与故障维护鲁棒集成优化方法

2 基于关键路径的启发式规则设计

在求解大规模问题时，插入性闲置时间一般随机产生，使得初始解性能和算法收敛性较差，需探索新的启发式规则，以生成具有高性能的初始解。考虑到闲置时间长度与加工序列、预防维护位置有强耦合关系，因此首先要找到关键路径并推导出各任务的闲置时间范围。

2.1 关键操作与关键路径

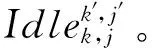
图2 关键路径示意图

路径一：O1,1→O1,2→O2,2→O3,2，则

路径二：O1,1→O2,1→O2,2→O3,2，则

路径三：O1,1→O2,1→O3,1→O3,2，则

从而可以得到：

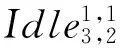
(1)

2.2 启发式规则设计

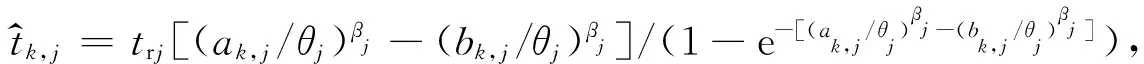
(2)

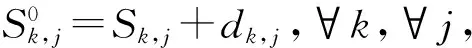
(3)

(4)

规则：插入性闲置时间dk,j在区间(uk,j,value/number)内进行初始化，所得到的解是可行的。

3 基于改进灰狼算法的闲置时间优化

灰狼优化算法是一种仿生群体智能算法，其模仿灰狼种群的社会领导层级机制和捕食行为，在每次迭代中选出最具竞争力的3只灰狼，领导其余个体包围猎物，进行捕食。考虑所研究问题的特殊性，在原有算法基础上加入了交叉算子[10]，以实现种群间的信息交流。

3.1 个体表示及适应度评价

初始种群中一半个体采用启发式规则在(uk,j,value/number)范围内生成，剩余个体随机生成。由于dk,j存在下界uk,j，为避免算法进化和交叉过程中产生不可行解，转换个体dk,j为Δdk,j，Δdk,j=dk,j-uk,j。

鲁棒优化一般是以调度计划鲁棒性作为优化目标。如式(5)所示，调度计划鲁棒性由制造周期鲁棒性与开始时间鲁棒性两部分线性加权求和，其中ρ1与ρ2是权重系数，ρ1+ρ2=1。

minz=

(5)

由于制造周期鲁棒性与最大完工时间有关，当案例规模较大时，制造周期鲁棒性的值远大于开始时间鲁棒性的值。在相同的工件加工序列下，为突出鲁棒优化性能，对目标函数进行等价转换，用插入性闲置时间d与推迟时长I展开目标函数式(5)：

其中，ρ1Cn,m仅与权重系数、工件加工序列有关，与闲置时间dk,j无关。因此，采用式(6)作为适应度评价函数：

(6)

3.2 控制参数C的确定

Rodriguez等[10]通过实验验证了灰狼算法中控制参数C(0

(7)

式中：T为算法运行时间；MaxIter为迭代终止条件，这里为算法最大运行时间。

3.3 进化机制及交叉算子设计

进化机制根据基本灰狼算法包围猎物原理，通过适应度函数选取最优的3只灰狼α、β和δ，引导其余灰狼包围猎物，实现位置更新。

基本灰狼算法中只有最佳的3只灰狼α、β、δ与其余灰狼存在信息交流，其余灰狼之间无信息交流。为了增强低等级狼群间的信息交流，改进算法融入交叉算子。考虑到个体Δdk,j是连续变量，采用线性重组的交叉方法。对于父代个体ch1和ch2，生成两个取值范围在[-0.25,1.25]的随机数α1和α2，交叉生成的子代个体表示为：

off1=α1ch1+(1-α1)ch2,

off2=α2ch1+(1-α2)ch2。

4 鲁棒集成优化算法流程

首先，使用NEH(Nawaz-Enscore-Ham)规则获得初始工件加工序列。其次，建立最大化可用性的预防维护周期模型，求解得到最佳预防维护周期。最后，使用双层循环算法优化调度计划的鲁棒性：内循环是改进灰狼算法，用于优化闲置时间；外循环通过邻域搜索确定最佳调度计划。算法流程具体如下。

输入:工件数(n),机器数(m),工件加工时长(p),故障维护平均时长(tr),预防维护平均时长(tp),机器失效函数参数(β和θ),种群规模(PS),交叉率输出:最佳调度计划步骤:1. 使用NEH规则获得初始工件加工序列;依据机器可用性,确定各机器预防维护位置。2. while邻域搜索不满足终止迭代次数do3. 使用启发式规则初始种群,计算所有个体适应度值,并确定领头狼α、β和δ。4. while灰狼优化不满足终止条件do5. fori=1toPSdo6. 更新参数C,根据领头狼更新当前狼的位置,计算适应度值。7. endfor8. 交叉生成新灰狼个体,计算新灰狼个体的适应度值。9. 更新领头狼α、β和δ。10. endwhile//终止改进灰狼算法11. 记录初始加工序列下的最佳调度计划鲁棒性以及无闲置时间的最大完工时间C0。12. 将初始加工序列下调度计划鲁棒性z0赋值给zbest,构建初始加工序列X0的邻域N(X0)。13. 随机选取邻域N(X0)中的序列X1,并记录序列X1下的最大完工时间C1。14. whileC1>101%×C015. 重新选取邻域N(X0)中的序列X1,并重新计算C1。16. endwhile17. 将序列X1下最优调度计划鲁棒性赋值给z1,比较zbest与z1,若z1

5 实验及结果分析

参照文献[11]，实验参数设置如下：工件数n={20,50,100,200}，机器数m={5,10,15,20}，存在16种n与m的组合方式；在任意组合方式下，工件加工时间pi,j服从均匀分布U[15,29]；Weibull分布的参数服从一定区间的均匀分布，θ=U[80,100]，β=U[2,4]；机器维护时长tr=U[5,10]，tp=U[15,20]。同时，目标函数中权重系数取ρ1=ρ2=0.5，利用相对百分误差(RPD)评估实验结果，RPD的具体计算公式为

(8)

式中：CTsol是算法求得的当前解；Bestsol是当前案例所有算法求得的最优解。

5.1 参数校验

由于参数对算法性能有很大影响，本文对相关参数都进行了校验。改进灰狼算法的参数水平是：种群规模{20,30,50}，交叉率{0.7,0.8,0.9}。通过全因素方差实验，每种参数组合运行5次，以5组数据中平均RPD作为评价标准。改进灰狼算法最佳参数组合是：种群规模为30、交叉率为0.8。限于篇幅，其余对比算法的详细参数校验分析暂不列出。

5.2 算法性能分析

在本文双层循环算法中，核心是旨在优化闲置时间的改进灰狼算法。为验证启发式规则及交叉算子的有效性，将基本灰狼算法、只融合交叉算子的灰狼算法、只融合启发式规则的灰狼算法、融合两处改进的灰狼算法进行对比。验证实验中采用了16个案例，每组案例运行10次，评价标准是RPD最小值和RPD平均值。图3所示为几种算法的RPD值95%置信区间。

(a)RPD最小值的95%置信区间

由图3可见，基本灰狼算法在16个案例下的平均相对误差达到58.6%，融合启发式规则的灰狼算法的平均相对误差有31.9%，融合交叉算子的灰狼算法的平均相对误差有12.9%，而经过两处改进的灰狼算法的平均相对误差仅有11.2%。实验结果表明，本文算法改进是有效的。

为验证改进灰狼算法的优越性，选取文献[8-9]中使用的遗传算法进行对比实验。同时，根据连续性优化问题的特点，另选取擅于优化连续性问题的粒子群算法以及近年来被广泛使用的人工蜂群算法进行对比实验。实验结果见表1，其中min是使用算法运行10次的最小适应度值，avg是10次运行的平均适应度值。由表1可见，改进灰狼算法性能最优。

表1 各算法的测试结果对比

算法鲁棒性的测试结果用RPD值表征，如图4所示。在相同的运行时间内，粒子群算法、人工蜂群算法、遗传算法的平均相对误差分别为262.8%、87.9%、40.8%，改进灰狼算法的结果最好，平均相对误差仅有6.9%，远远小于其余3种群智能算法，进一步验证了该算法的优越性。

(a)RPD最小值的95%置信区间

5.3 灵敏度分析

本文的优化目标是系统鲁棒性，由制造周期鲁棒性和开始时间鲁棒性两部分线性加权求得。权重系数的取值将直接影响最终优化结果，因此需对权重系数进行灵敏度分析。选取一个案例：m=5、n=20，设定制造周期鲁棒性的系数ρ1从0.9逐渐减小至0.1，而ρ2=1-ρ1。随着权重系数ρ1的变化，制造周期和开始时间的鲁棒性变化情况如图5所示。

图5 制造周期和开始时间的鲁棒性随权重系数的变化

由图5可以看出，随着ρ1的减小，优化目标中制造周期鲁棒性所占比重逐渐减小，开始时间鲁棒性所占比重逐渐增大。在此过程中呈现的变动趋势是：制造周期鲁棒性变动幅度逐步减小，而开始时间鲁棒性变动幅度逐步扩大。若决策者更重视开始时间鲁棒性，须设置ρ1<0.5，以制造周期鲁棒性的降低为代价来换取开始时间鲁棒性的提升。

5.4 鲁棒性分析

以案例1为对象进行系统鲁棒性分析，运用蒙特卡洛方法模拟故障场景。图6(a)是不含闲置时间的调度计划甘特图，图6(b)是含闲置时间的调度计划甘特图，图6(c)和图6(d)是两种故障维护情形下的调度计划甘特图。图中绿色区域表示工件加工区间，红色区域表示预防维护区间，蓝色区域表示故障维护区间。

比较图6(a)和图6(b)，不含闲置时间调度计划的最大完工时间Cmax=631，含闲置时间调度计划的Cmax=656.98，可见闲置时间的插入确实在一定程度上延长了制造周期，松弛了生产节奏。从图6(c)和图6(d)可得，在故障维护情形下Cmax分别等于711.59和693.85，与不含闲置时间的调度计划相比Cmax分别延长12.78%和9.96%，与含闲置时间的调度计划相比Cmax仅分别延长8.31%和5.61%。这表明闲置时间的插入吸收了故障维护对工件加工的影响，保证更多的工件能在原计划开始时间开始，而所有工件尽可能在原定制造周期内完成加工，即调度方案更具鲁棒性。

(a)不含闲置时间的调度计划

6 结语

本文提出基于双层循环的车间调度与设备维护鲁棒集成优化算法，内层循环使用融合启发式规则的灰狼算法优化闲置时间，外层循环通过邻域搜索优化加工序列。针对内层循环的闲置时间设置，提出基于关键路径的启发式规则，以提高初始解性能；提出融入交叉算子的混合灰狼算法，以加强低等级狼群的信息交流。实验结果证明了启发式规则的有效性以及改进算法的优越性。在未来的研究中，可尝试将本文方法推广应用到柔性流水车间调度，也可以继续挖掘工件加工序列对系统调度鲁棒性的影响。