基于数据增强与自编码GRU网络的多规格热轧带钢精轧电耗预测

肖 雄，刘天恒，张 飞，王 京，赵云涛

(1.北京科技大学工程技术研究院，北京，100083；2.武汉科技大学信息科学与工程学院，湖北 武汉，430081)

近年来，能源介质监测管理作为推进钢铁行业智能制造发展的重点之一，如何实时有效地掌握钢铁生产过程中能源消耗分布情况及各生产工序的能耗需求是实现深度节能及智能排产的关键所在。

针对钢铁企业厂级和产线级能源介质预测及优化问题，国内外已有大量研究报道。如李艳[1]从钢铁企业能源管理系统的基本状况入手，对能源管理系统的智能优化模块进行了阐述；田军吉[2]就钢铁行业如何实现节能减排及智能化控制进行了探索与分析；Porzio等[3]从煤气利用效益最大化和二氧化碳排放最小的角度出发，分析并提出了煤气系统多目标优化求解算法；Ashok等[4]提出一种适合工业热电联产系统的最优能源优化分配模型；张颜颜等[5]提出一种数据驱动的粒子群算法优化子空间方法，成功预测了钢铁生产过程中各工序的能源消耗；田玉前等[6]针对武钢炼铁系统建立多级能源投入产出模型，并分析了系统能耗与节能潜力。

目前，钢铁企业能耗预测研究多集中于厂级或产线级，缺乏对关键工序能耗的精细化预测，尤其是自动化程度较高的轧制过程各关键工序。热轧作为轧制生产的典型过程，对其开展能源介质预测及优化研究具有重要价值。而在带钢热轧工序所涉及的能源介质中，热轧吨钢电耗是最显著的一项经济指标。

为此，本文以热轧精轧段工序为研究对象，拟建立模型对多规格轧件的轧制电耗进行预测。但实际上，热轧电耗相关数据具有样本分布不均衡、维数高、复杂性强等特点，故本研究拟将深度学习算法应用于精轧段带钢轧制电耗预测问题上。模型选择方面，门循环单元(Gate recurrent unit，GRU)网络擅于处理高维序列数据且具有网络层次深的优点[7]；数据优化方面，Arjovsky等[8]首次提出Wasserstein距离生成对抗网络(WGAN)，其改进了传统生成对抗网络在数据增强方面的不足；在预测模型的组合优化方面，徐子弘等[9]将自编码器与GRU网络结合，提供组合预测模型新思路，张立峰等[10]将卷积神经网络与GRU网络结合，实现短期负荷预测。

基于此，本文提出一种基于数据增强和自编码的GRU网络模型，对多规格热轧带钢精轧电耗进行预测，并基于某企业厂级实时数据对所提出算法的有效性进行验证。

1 精轧过程分析及模型设计

1.1 精轧过程数据变量关联特点

图1所示为热轧工艺流程图，可以看出，该过程主要包括加热、粗轧、精轧、层流冷却及卷取工序，其中精轧段耗电量大、工艺复杂。本文主要针对精轧段的轧制电耗进行预测研究，主要是因为：①精轧区自动化程度高，数据采集较为便捷，现场控制系统及其二级系统可以提供大量的统计数据；②现场按照生产计划进行排产，所采集数据呈规律性变化；③多规格产品生产提供了多样化的生产数据。

轧机传动装置及主辅电机的电耗是精轧电耗的主要来源。与精轧段电耗相关的数据主要包括能源介质数据、生产过程数据和生产管理数据。这些数据贯穿了生产层、控制层等多层级结构，具有耦合性强、复杂性高的特点，需进行降维处理。此外，由于采集数据样本分布不均且质量较低，而通过数据驱动方式构建的预测模型需要基于大量高质量数据，故如何在解决数据质量问题的同时实现高精度模型预测显得尤为重要。

1.2 GRU网络

精轧电耗数据在类型上属于序列数据，循环神经网络(Recurrent neural network, RNN)是一类处理序列数据的网络，其中GRU网络与长短期记忆网络(Long short term memory, LSTM)是RNN的两种变体结构。LSTM模型在每个神经元内部加入输入门、遗忘门和输出门，用于解决长序列训练过程中的梯度消失和梯度爆炸问题；GRU网络模型是由Cho在2014年提出的改进版LSTM模型[7]，其进一步简化门结构为更新门与重置门，在提升训练效率的同时确保预测精度与LSTM模型相似。GRU单元结构如图2所示。

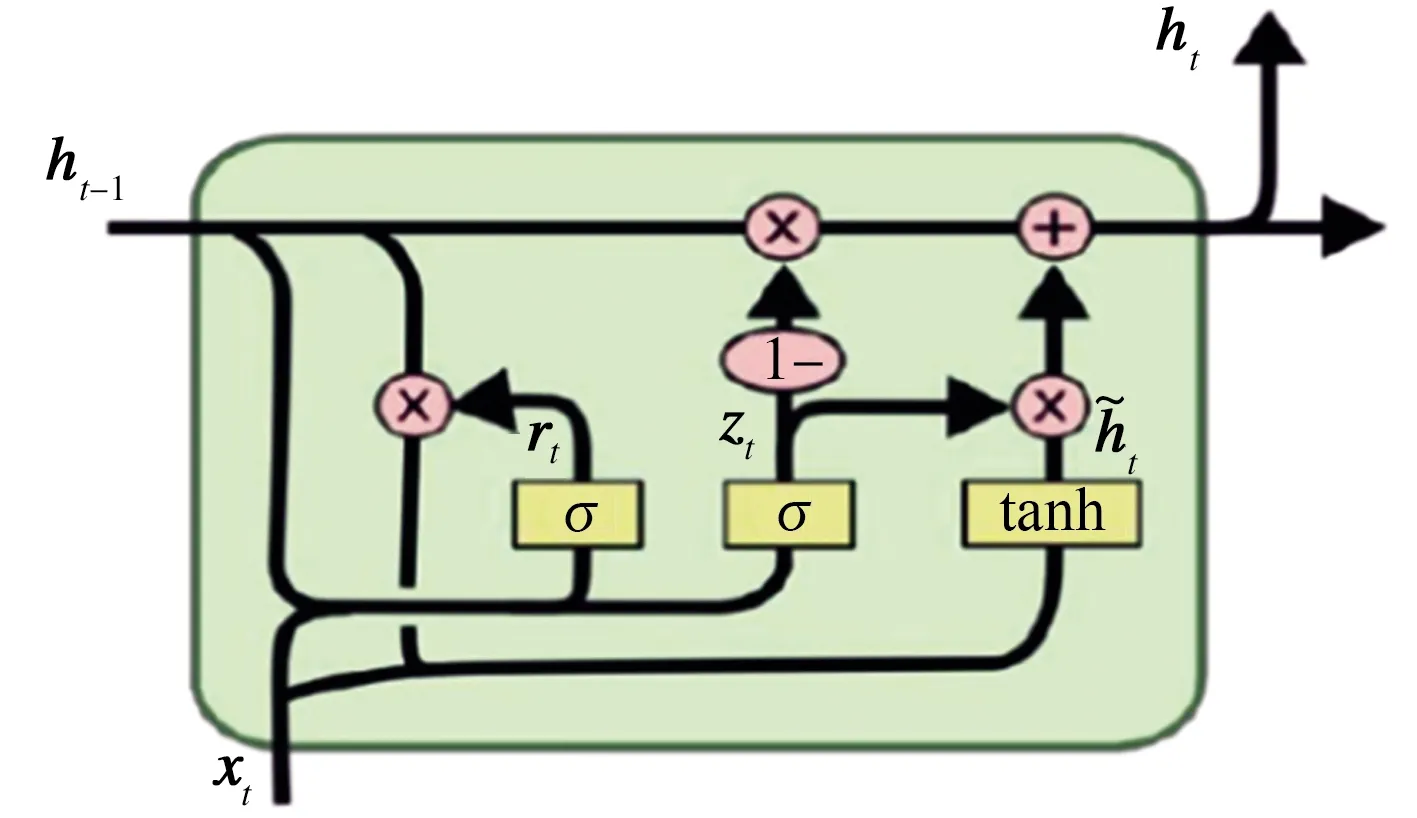
图2 GRU网络单元

图2中，zt表示更新门，用来决定当前的隐藏状态ht能接收上一隐藏层的多少信息，经过Sigmoid函数将结果映射到0～1之间，即：

zt=σ(Wh*xt+Wz*ht-1)

(1)

rt为重置门，决定上一时刻隐藏层状态有多少信息需要被遗忘，经过Sigmoid函数将结果映射到0～1之间，越接近1的信息越容易被保留，即：

rt=σ(Wr*xt+Ws*ht-1)

(2)

将重置门rt与ht-1进行Hadamard乘积，决定当前记忆内容中要遗忘多少上一时刻的隐藏层内容，然后与新的输入数据结合放入tanh激活函数中，即：

(3)

最后，确定当前隐藏层保留的信息，通过zt和1-zt确定哪些历史数据和当前数据需要更新，即：

(4)

上述式中：Wt和Wu均表示权重；σ表示Sigmoid函数。

1.3 基于GRU网络的电耗预测模型

本文选取能源介质数据、生产过程数据和生产管理数据共同组成能耗数据库，利用钢卷号和精轧工序的时间标号可以实现对所选每一块轧件进行能耗相关数据的提取。经过数据完整性检验后，先将数据送入预处理单元进行处理。数据预处理模块包含两项任务：①去除因故障停机、停产整修生成的异常数据；②对统计数据中的空白数据和残缺数据进行填补修正。随后，对所得数据进行归一化处理，以形成模型训练和验证的规范数据流信息。使用训练集对GRU预测模型进行训练，并用验证集对预测模型的性能进行验证，此处的预测结果需经过反归一化处理，以使预测结果更加直观。图3所示为基于GRU网络的精轧电耗预测模型结构示意图。

图3 基于GRU网络的精轧电耗预测模型结构图

1.4 算法存在的问题及改进方案

GRU网络可较好地处理高维序列数据，并且预测精度较高，但其训练依赖高质量数据，而历史电耗数据的采集频率与轧制过程数据的采集频率不一致，导致样本数据分布不均衡，此时需结合数据增强方法生成高质量数据，防止过拟合，进而提升模型预测精度。另外，将高维数据直接输入GRU网络效率较低，若能选择合适的降维手段，在不破坏数据主要输入特征的前提下实现数据降维，则能提升模型效率。针对上述问题，本文从数据处理及模型组合层面，利用数据增强和自编码对精轧电耗模型进行优化。

2 数据优化及模型改进

2.1 数据选取

为实现对多规格带钢电耗的预测，需在数据集中加入规格数据，即利用含碳量等材质类数据对不同规格带钢进行区分。

本模型选取的数据是某热轧厂生产线的能耗相关数据，来源是厂级能源管控计量二级系统。在所有数据中，排除了因故障停机和整修阶段电力损耗不正常的数据，本研究共采集383组电耗相关的轧钢过程数据以及同时段下190组历史电耗数据。结合轧制生产指标和对轧制工艺原理的分析，选定与精轧阶段电耗有关的能耗相关指标共45个，包括碳含量、带钢重量、轧制温度、F1～F7轧机轧制速度、H1～H7轧件厚度、压下量、产品宽度和厚度等。

2.2 生成对抗网络与数据增强

生成对抗网络(Generative adversarial networks, GAN)是一种深度学习模型，主要由生成器(Generator)和判别器(Discriminator)组成。生成器与判别器博弈对抗，不断优化生成更真实数据，判别器则是分辨真伪数据。图4为生成对抗网络的结构示意图。

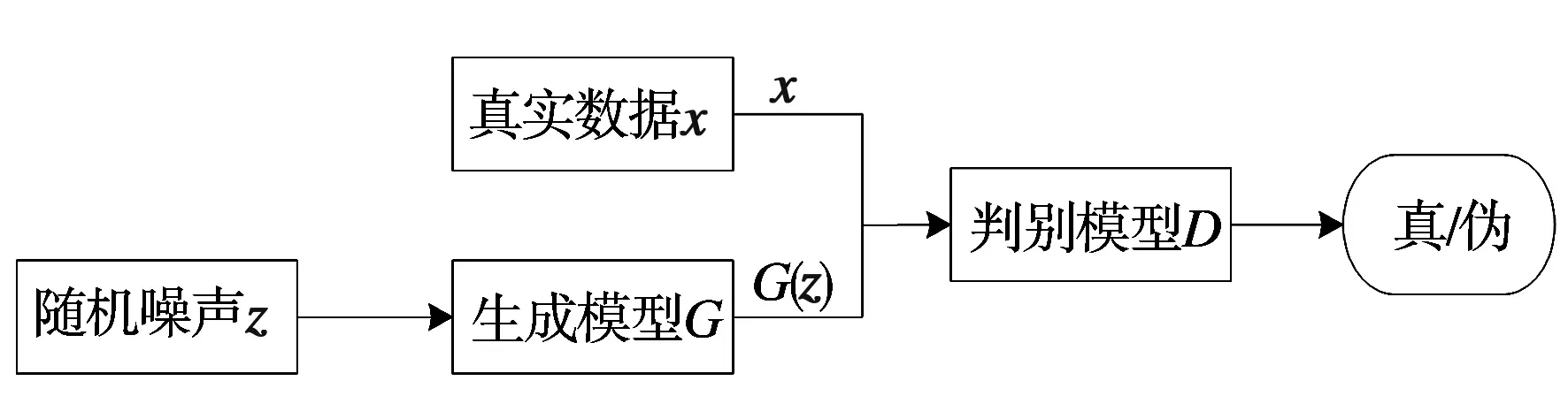
图4 生成对抗网络结构

GAN的学习优化过程是一个极小极大化问题，其目标函数可以描述为：

+Ez～Pz(z)[lg(1-D(G(z)))]}

(5)

GAN训练过程中，生成器输入的是一组随机噪声z，输出为生成样本G(z)，与真实样本分布相似。判别器输入的是生成样本G(z)和真实样本x，输出是一个用于区分真实样本和生成样本的概率值。

由于JS散度可能会导致GAN训练不稳定和模式崩塌等问题，WGAN应运而生，其主要有以下改进：①舍去判别器最后一层的Sigmoid激活函数；②生成器和判别器的损失不再取对数；③优化网络时不再采用Momentum和Adam等算法，而采用RMSProp及SGD 优化算法；④WGAN限制判别器每次更新参数后，其绝对值不能超过一个固定常数c。

加入惩罚项的WGAN损失函数可表示为：

V(G,D)=

(6)

式中：λEx～Ppenalty(·)为惩罚项，用于促使判别器输出D(x)变得足够平滑，使模型收敛；Ppenalty(x)是指介于真实数据Pdata(x)和生成数据Pz(z)间的数据;∇xD(x)表示对x求导数。

WGAN训练过程中，利用Wasserstein距离来表示生成数据的可靠性。其相比于KL散度和JS散度的优势在于，即使两个分布的支撑集没有重叠或重叠部分非常少，仍能反映两个分布的远近，而JS散度在此情况下为常量，KL散度可能无意义。该值越小表示生成对抗网络训练的越好，生成器生成数据的质量越高，Wasserstein距离可表示为：

(7)

对于所有可能的联合分布集Π(P1,P2)下的每个可能联合分布γ，可以从中采样(x,y)～γ，并计算出这对样本之间的距离‖x-y‖以及样本对距离的期望值E(x,y)～γ[‖x-y‖]。在所有可能的联合分布中，该期望值所取到的下界即为Wasserstein距离。

2.3 数据降维

本文选定的45个与精轧电耗相关指标，维数相对较高且数据间存在强耦合关系，这会增加模型的运算复杂度并且延长计算时间。而引入自编码器对数据进行降维，可在保持模型预测精度的同时，节省计算时间。

自编码器(Autoencoder, AE)是一类在半监督学习和非监督学习中使用的人工神经网络，其功能是通过将输入信息作为学习目标，对输入信息进行表征学习，其结构如图5所示。

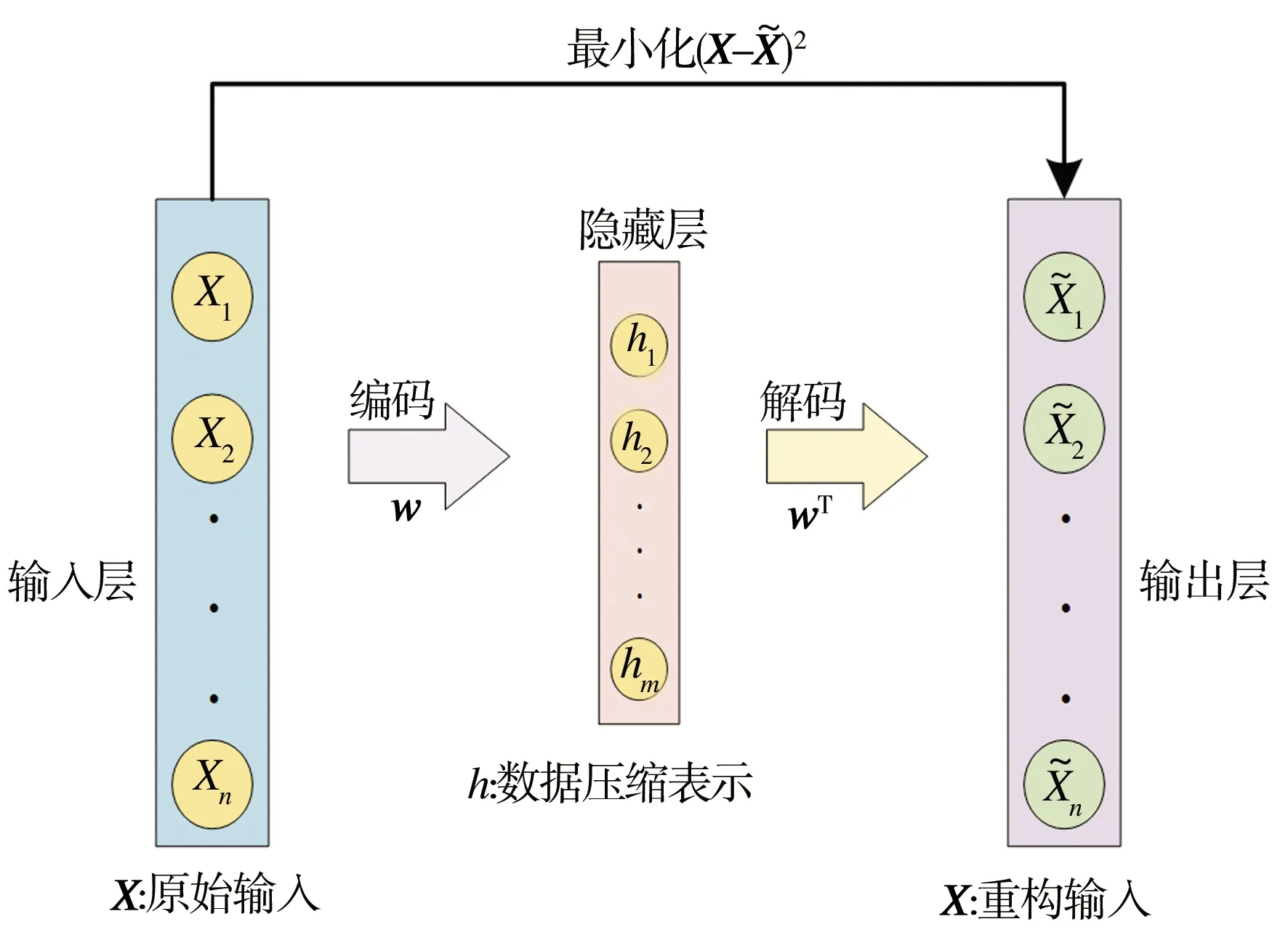
图5 自编码器结构

自编码器包括编码与解码两个阶段，其中数据降维对应于编码阶段，具体过程如下：

首先，输入45维电耗数据X={X1,X2,…,X45}，自动编码器将X映射到一个隐藏层，利用隐藏层结构将数据压缩为h={h1,h2,…,hm}，综合考虑维数、解码输出与输入均方误差(MSE)不大于0.8等因素，m值取6。隐藏层神经元个数表征了高维输入数据的本质维度，隐藏层输出h的具体形式为：

h=σ(w·X+b)

(8)

式中：σ为Sigmoid函数；w为输入层到隐藏层之间的权重系数；b为偏置项。

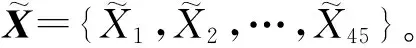
(9)

式中：wT为隐藏层到输出层之间的权重系数，C为偏置项。

通过规划输入信号与解码后重构输出信号的均方误差最小问题，得到w、b、wT、C值，最终完成网络训练。

2.4 基于数据增强和自编码GRU网络的精轧电耗预测模型

WGAN中生成器与判别器均由神经网络全连接层构成，与原生GAN不同，WGAN判别器最后一层没有连接Sigmoid激活函数，模型结构如图6所示。

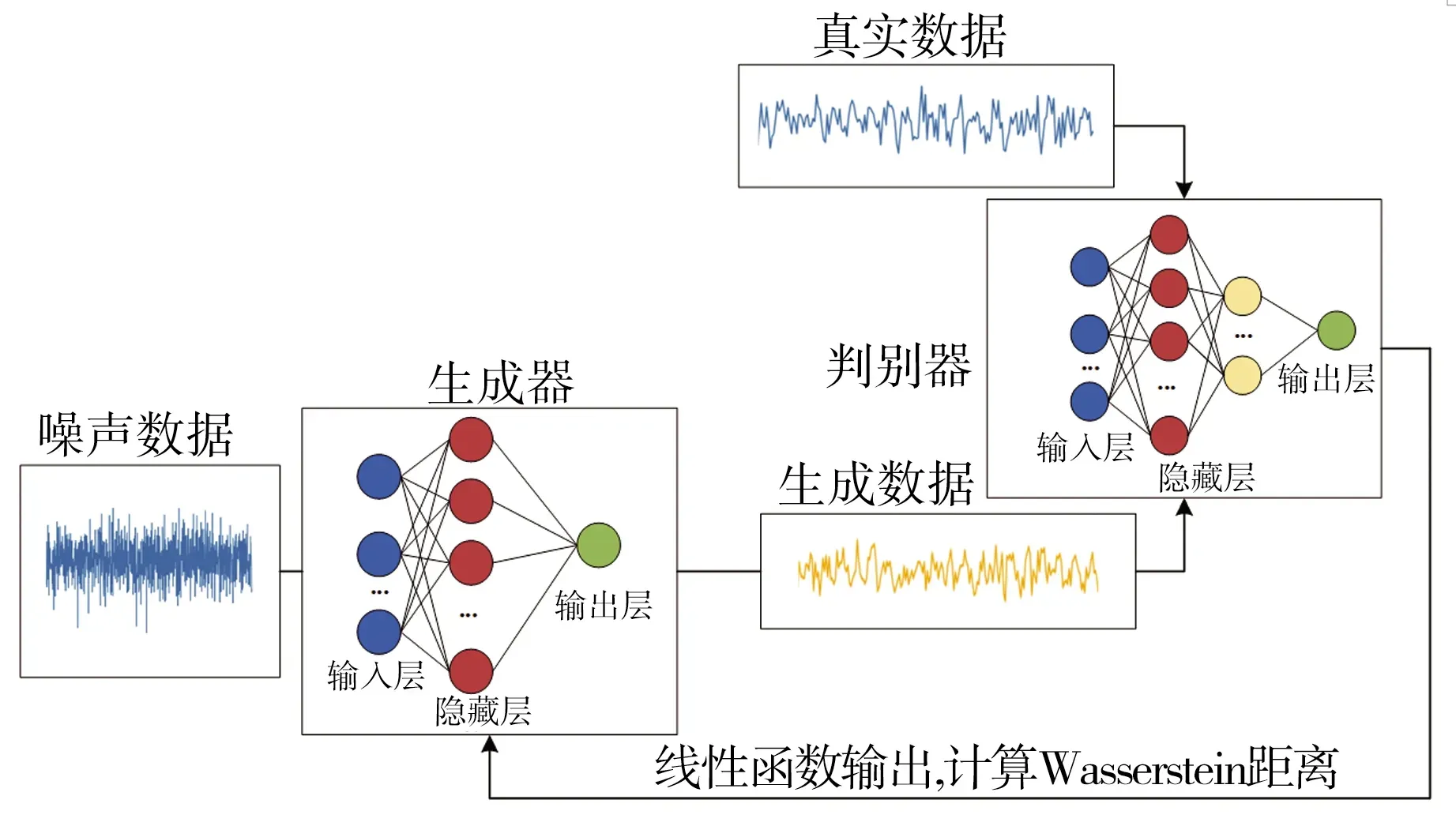
图6 WGAN结构

生成器的输入是随机生成噪声数据z，输出是具有和真实数据分布相似的生成数据；判别器的输入是生成样本G(zi)和真实样本x，输出是一个线性函数的计算结果，目的是为了计算Wasserstein距离。WGAN的主要训练步骤如下：

(1)创建生成器G并初始化其权重参数θg，然后将生成器固定；创建判别器D并初始化其权重参数θd，通过式(10)作为损失函数来训练D，式中加入惩罚项Ex～Ppenalty(·)，目的是为了让D收敛。采用梯度上升方式(式(11))更新参数来最大化损失函数VD，进而提升判别器D的辨别能力，η表示学习率。

λEx～Ppenalty (x)[(‖∇xD(xi)‖-1)2]

(10)

θd←θd+η∇VD(θd)

(11)

(2)固定判别器D，开始训练生成器G。G的损失函数如式(12)所示，采用梯度下降法(式(13))最小化损失函数VG，从而使其生成更真实的数据样本。

(12)

θg←θg-η∇VG(θg)

(13)

(3)为使生成的样本尽可能真实，每训练5次判别器D后，训练一次生成器G。经过多轮对抗训练后，WGAN达到纳什均衡，即可以从生成器中得到大量的样本数据。

图7为AE-GRU的网络结构图，可以看出，该结构分为AE和GRU网络两部分。AE功能是提取输入数据{X1,X2,…,Xn}的高阶特征并降低其维度。GRU网络功能是接收自编码器输出的高质量低维特征作为输入，经GRU层与全连接层的深度学习与分析后，最终输出得到精轧电耗预测结果。

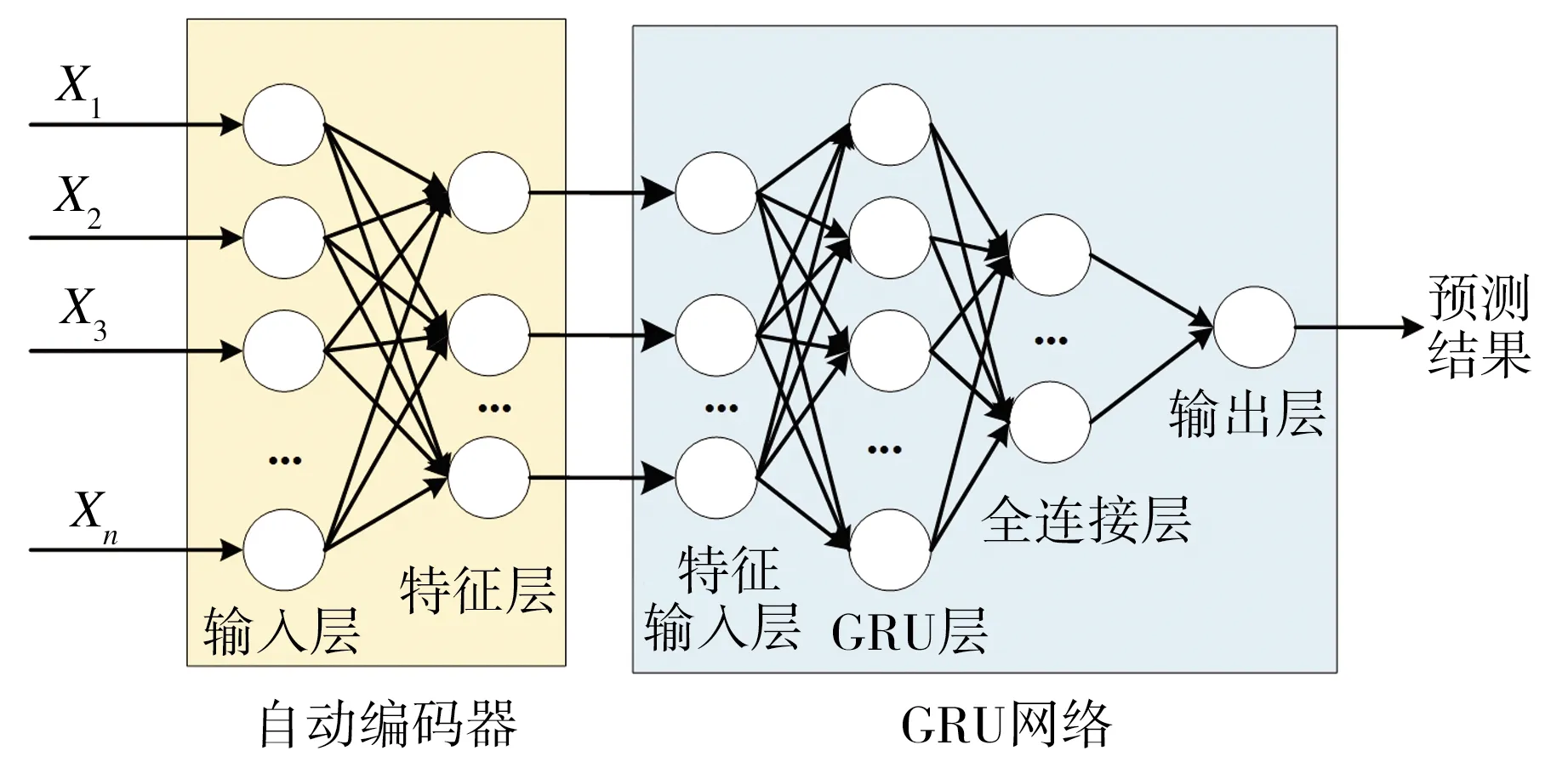
图7 AE-GRU网络结构

综上所示，本文构建了基于数据增强和自编码GRU网络的精轧电耗预测模型(WGAN-AE-GRU)，其结构如图8所示。从图8可以看出，WGAN-AE-GRU由数据增强部分和AE-GRU网络预测模型构成。数据增强部分利用生成对抗网络WGAN，针对样本中的低频采集数据(如历史电耗数据)来训练生成器与判别器，生成高质量电耗数据，扩充原有数据集；AE-GRU网络预测模型部分基于已有的充足数据样本，对45个电耗相关指标进行降维与特征重构，得到5维特征，并结合历史数据构成6维特征，作为解码器GRU网络的输入特征，最终得到预测结果。

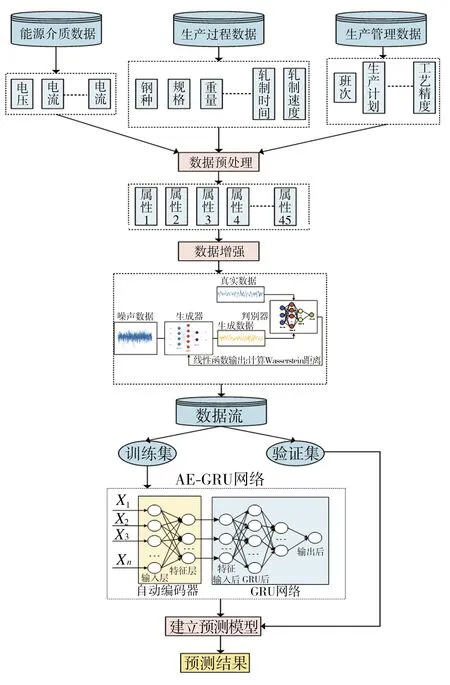
图8 WGAN-AE-GRU结构图

3 算法仿真与性能验证

本研究在Windows 10操作系统下进行，CPU为Intel®CoreTMi5-7300，显卡为NVIDIA GeForce GTX 1050Ti，计算机内存为8 GB，所用语言为Python 3.7，深度学习框架为TensorFlow 2.0。

3.1 评价指标

本文使用均方误差(MSE)和决定系数(R2)来评估模型预测效果。MSE表示预测值与实际值的平均误差，MSE越小，预测性能越好；R2表示模型输出波动能够被模型输入波动所描述的百分比，其值越趋近1，模型的描述能力越强。

3.2 基于GRU网络模型的预测性能验证

分别使用BP神经网络、支持向量机(SVM)和GRU网络对精轧过程电耗进行预测，3种模型的预测曲线及描述能力随迭代次数的变化曲线如图9所示。GRU网络的结构设计为：一层输入层+两层GRU层+一层输出层，由于输入数据为选取指标和历史电耗数据，故输入层的神经元个数为46个，输出层数据为模型的最终预测值，对应神经元个数为1个；激活函数采用ReLU函数，优化器采用Adam，学习率为0.01，dropout为0.5，采用L2正则函数，训练epoch为500次，原始数据样本按照8∶2划分训练集与测试集。

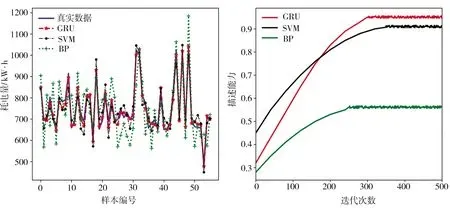
(a)电耗预测值 (b)描述能力

3种模型的预测对比结果如表1所示。结合表1和图9可知，相比BP神经网络和SVM模型，GRU网络预测模型表现更佳，MSE值最低且R2最接近1，表明该模型具有更高的精度和更好的描述能力。

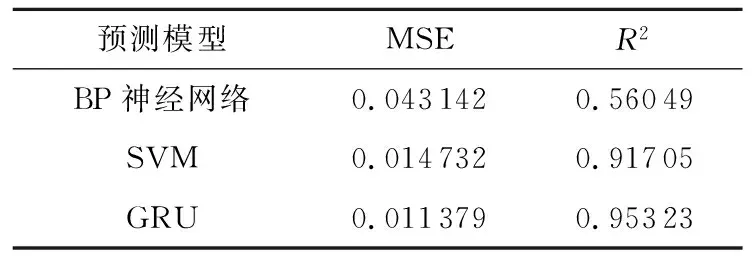
表1 不同预测方法的评价指标

3.3 基于AE-GRU网络模型预测性能验证

AE-GRU模型的自编码器层中，通过解码器对编码器降维得到的5维特征进行重构，利用ReLU激活函数输出稀疏性，减弱模型对权重参数的依赖；GRU层包含2层，优化器为Adam，批处理量为32，学习率为0.01。设置dropout层随机失活50%的神经元与L2正则函数，以防止模型过拟合。分别利用GRU与AE-GRU网络模型对原始样本集进行训练，不同方法的评价指标如表2所示。由表2可见，相比于GRU网络模型，AE-GRU网络模型的训练时间减少了2.969 s，节省约一半的时间，并且两种预测模型的MSE和R2接近，表明AE-GRU网络模型基本保持了GRU网络模型的预测精度和描述能力。

表2 GRU和AE-GRU模型的评价指标

3.4 基于WGAN-AE-GRU网络模型预测性能验证

WGAN模型中生成器和判别器均由全连接网络构成。生成器包括输入层(输入维数为46，输入数据为随机高斯噪声)、一层隐藏层(隐藏单元数为128，使用Sigmoid函数激活)和一层输出层(输出为生成电耗数据，对应为判别器的输入)；判别器包括输入层(输入包含真实样本标签与生成电耗数据)、两层隐藏层(分别包含128和256个单元，不用Sigmoid函数激活)和一层输出层(输出一维线性函数计算值用于计算Wasserstein距离，从而判别生成数据质量)。判别器同生成器相互博弈实现纳什均衡。此外，WGAN模型使用SGD优化器进行优化，WGAN总训练epoch设置为3000次。

图10所示为100组历史电耗数据和WGAN网络生成结果对比，可以看出，尽管通过WGAN网络生成的样本并不能完全拟合真实数据，但经过3000次迭代后，用以表示Wasserstein距离的损失值仅为0.125 73，表明整体分布与真实数据基本吻合。由此可见，WGAN网络具有相应的表征能力，可用于扩充原有的数据集。

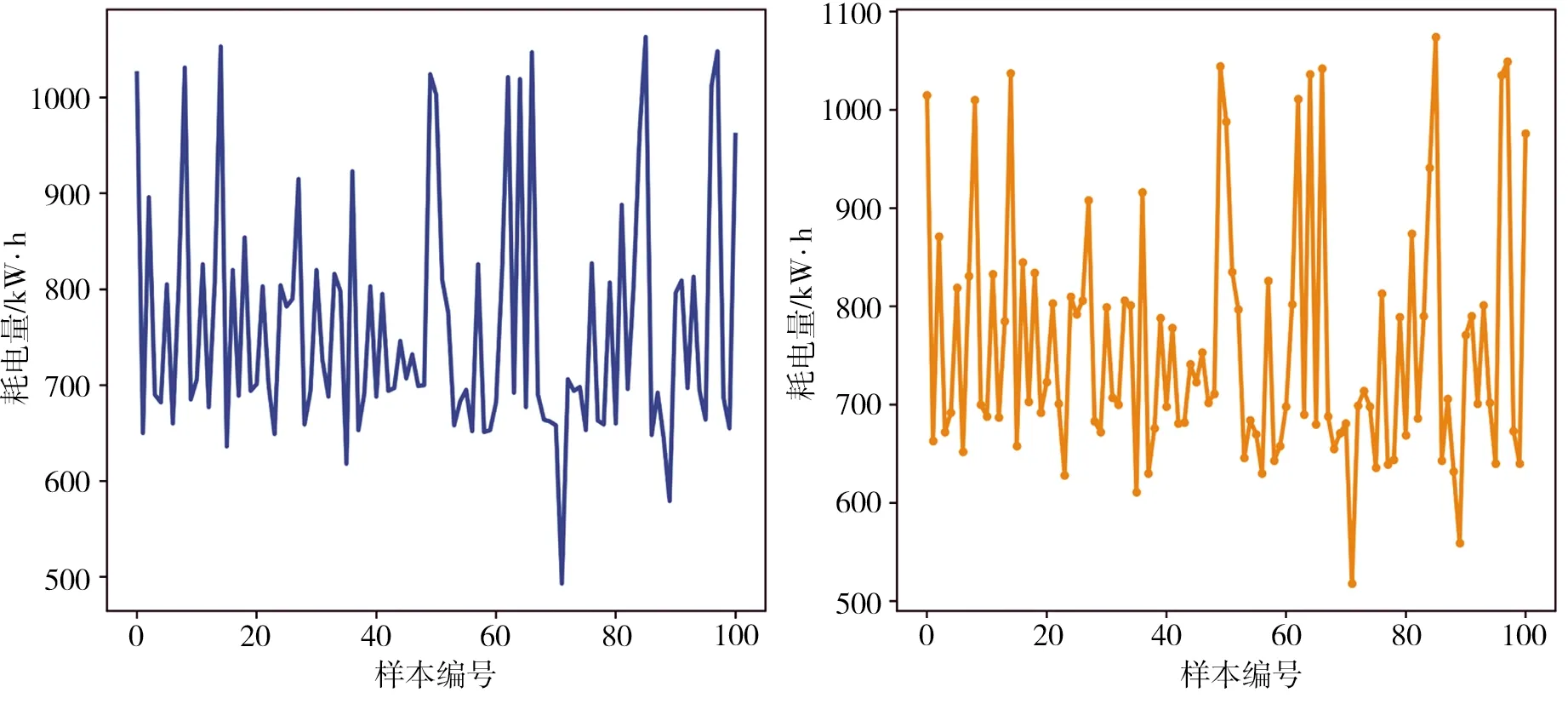
(a)真实数据 (b)生成数据

图11所示为训练WGAN模型的生成器和判别器损失函数变化趋势，可以看出，当迭代次数达到2200左右时，生成器和判别器的损失函数值均从较高值下降至1附近并保持小幅震荡，表明WGAN模型达到纳什均衡。

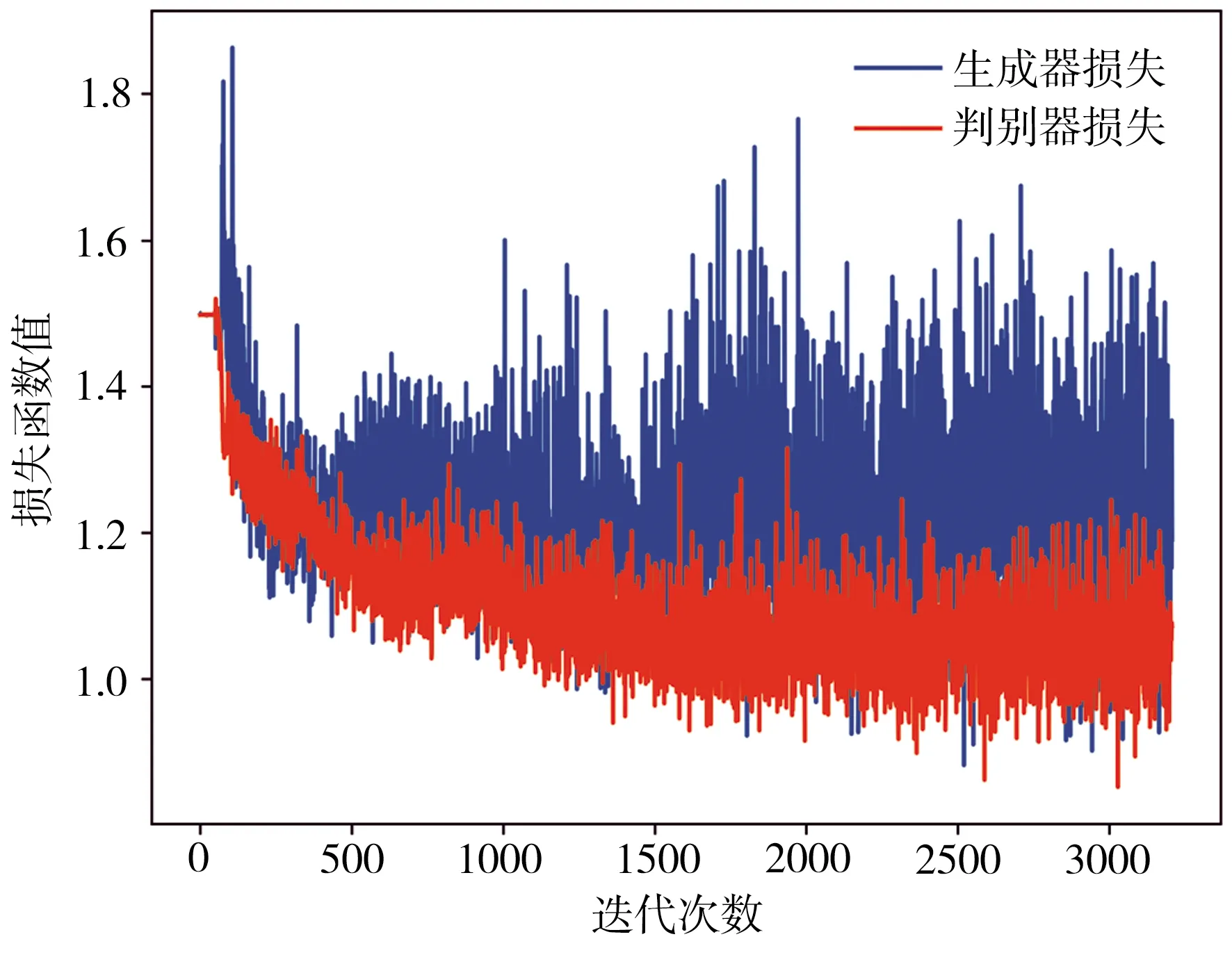
图11 生成器与判别器损失函数随迭代次数变化

另外，为验证数据样本的质量和数量对模型预测准确性的影响，将原始样本数据集和处理后不同数量的样本带入WGAN-AE-GRU网络模型进行计算，得到评价指标如表3所示。由表3可见，在利用WGAN网络解决样本分布不均衡问题并提升原始数据样本质量后，模型描述能力和预测精度显著提高；增加两倍样本数量时，模型预测误差降低幅度有所变缓，模型描述能力小幅提升；增加三倍样本数量时，模型描述能力达到饱和，预测误差基本保持不变。

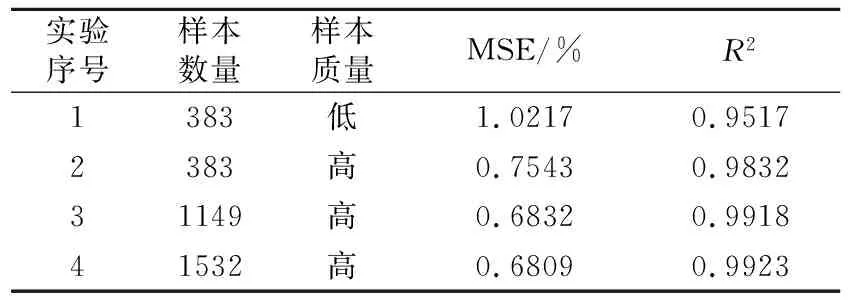
表3 数据样本对WGAN-AE-GRU模型预测性能影响

图12和表4分别为利用WGAN-AE-GRU、AE-GRU和GRU三种模型得到的的精轧电耗预测曲线和评价指标，其中WGAN-AE-GRU模型是采用WGAN网络生成的高质量数据样本进行的预测，后两者则是在原始样本下进行的预测。结合图12和表4可知，WGAN-AE-GRU模型预测曲线与真实数据的拟合效果更好，相比于AE-GRU与GRU模型，WGAN-AE-GRU模型具备更高的模型预测精度和更低的均方误差，表明其预测精度和描述能力最佳。

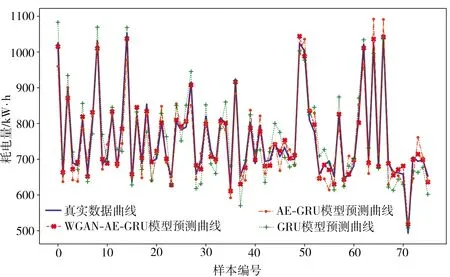
图12 GRU、AE-GRU和WGAN-AE-GRU模型的预测曲线

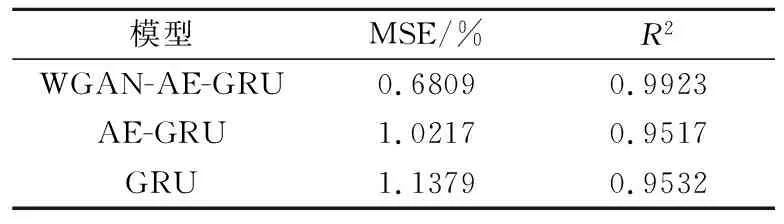
表4 GRU、AE-GRU和WGAN-AE-GRU模型的评价指标

3.5 多规格轧件电耗预测验证

选取某钢厂量产的P3A2、Q235B、Q345B、WL510和SPHC五种钢，分别利用GRU、AE-GRU和WGAN-AE-GRU模型对其进行电耗预测，不同钢种选取500组数据进行实验，得到三种模型的预测效果对比如图13所示。由图13可见，相比于未经数据增强的两种模型，WGAN-AE-GRU模型精轧电耗预测误差均明显较低，AE-GRU模型的预测误差略低于GRU网络模型。综合前文分析，AE-GRU模型具有更高的训练效率(计算时间最短)。另外，五种钢种的预测结果表明，WGAN-AE-GRU模型可以实现多规格热轧件精轧段电耗的精确预测。

图13 GRU、AE-GRU和WGAN-AE-GRU模型预测误差对比

4 结语

本文针对多规格带钢精轧电耗预测问题，提出了一种基于数据增强和自编码GRU网络的精轧电耗预测模型(WGAN-AE-GRU)。WGAN生成对抗网络能有效解决数据样本不均衡问题，提高了数据样本质量；AE-GRU网络模型充分结合了自编码器的数据降维功能与GRU网络的高精度预测功能，在节省计算时间的同时实现高精度电耗预测。而WGAN-AE-GRU模型在数据处理和预测精度方面，较上述两种模型又有显著提升，并且该模型能被应用于多规格轧件精轧电耗的预报。另一方面，经实际生产数据验证该预测模型的准确性后，该模型也能对一些未生产的带钢种类进行电耗预测，可以满足产线级轧制电耗预报的需求，具有比较突出的现实意义。