液滴大小与蒸发温度之间的定量关系研究

李 广，左学勤，杨 群，丁宗玲，郑赣鸿

(1.安徽大学 材料科学与工程学院，安徽 合肥 230601；2. 安徽大学 物理与光电工程学院，安徽 合肥 230601)

物质的多相共存是热力学平衡的普遍现象，如某种物质的液态和气态、固态和气态、固态和液态两相共存或固态、液态和气态三相共存。在多相平衡状态时，根据热力学平衡条件可以获得很多状态参量之间的关系。比如与实验结果符合非常好的克拉珀龙(Clapeyron)方程[1]，它给出了两相共存时平衡曲线斜率，即dp/dT与两相间的相变潜热、相变前后两相的摩尔体积差之间的定量关系式。又如，考虑到表面相的影响，从液滴与蒸汽的两相共存平衡条件出发，可以导出液滴在其蒸汽中的形成条件。如果进一步假设蒸汽相为理想气体，可以导出在一定温度和蒸汽压强下，液滴与蒸汽达到平衡时的中肯半径[2]。但是，在更多时候不能视蒸汽为理想气体。同时，在实际生活中往往可以发现，液滴半径较小时更容易蒸发，即其蒸发温度比相应大块液体低。此外，在材料研究领域，纳米颗粒材料的熔化温度小于其块材熔化温度，即将材料做成纳米尺度后，其熔融烧结温度将明显低于相应的固体大块材料。就这些问题，若从单元系的液滴和蒸汽两相共存的热力学平衡条件出发，视液滴表面张力引起的压强相对于蒸汽相压强为一级小量，便可导出液滴蒸发温度与其半径大小之间的定量关系式。同样，也可以解释为何纳米颗粒材料的熔化温度低于其块材熔化温度。

1 液滴与蒸汽共存时热力学平衡条件

如图1所示，设当前的孤立系统仅由一种组元构成。在一定的温度下，有三个相共存：用I表示某种物质的气相(蒸汽)，II表示该物质的液相(液滴内部液体)，由于该液相的形状为球形，还有液滴的表面相，记为第III相。三者构成一个孤立的热力学系统。根据热力学知识，简要导出这三相平衡时必须满足的条件。

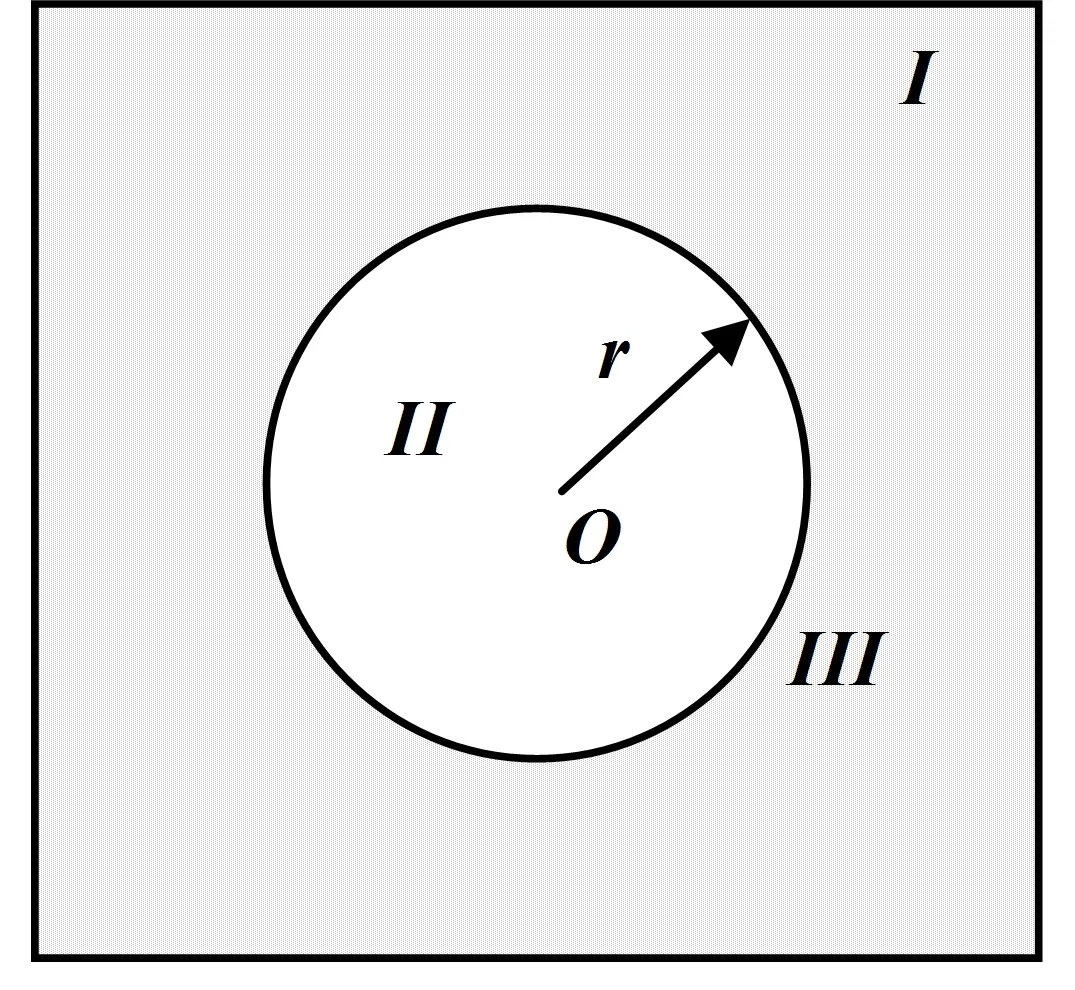
图1 液滴和其蒸汽两相系统示意图

首先，列出以温度T、压强P和物质的量n为状态参数的每相内能的热力学基本状态方程：dUi=TidSi-PidVi+μidni(i=I，II和III)：

dUI=TIdSI-PIdVI+μIdnI

(1-1)

dUII=TIIdSII-PIIdVII+μIIdnII

(1-2)

dUIII=TIIIdSIII-PIIIdVIII+σdA+μIIIdnIII

(1-3)

其中，μi表示第i相的化学势；σ是液滴的表面张力，单位为J/m2，A是其表面积。

第二步，由于这三相共存是一个孤立系统，气液两相之间可以相互转换。设想在温度和总体积保持不变的条件下，孤立系统内部各相之间发生一个微小的虚变动，三相物质的量、体积和表面积分别有δni、δVi和δA的变化。由于虚变动中系统的总内能、总物质量和总体积保持不变，膜厚很薄时，膜可以理想化为几何面，其表面物质的量nIII=0，进而dnIII=0；VIII=0，dVIII=0；其内能UIII=0，dUIII=0。据此，式(1-3)可简化为(2)式：

TIIIdSIII+σdA=0

(2)

进一步，可以得到虚变动的约束条件：

UI+UII=常数，δUI+δUII=0

(3-1)

VI+VII=常数，δVI+δVII=0

(3-2)

nI+nII=常数，δnI+δnII=0

(3-3)

第三步，在这个虚变动中，可以得到每相的熵变如下：

(4-1)

(4-2)

(4-3)

假设液滴为球形，液滴的体积为VII=4πr3/3，A=4πr2。所以，δVII=4πr2δr，δA=8πrδr。由此可得，δA=2δVII/r。于是，系统的总熵变可记为：

(5)

当三相达到热力学平衡时，要求

δS=0

(6)

当膜很薄时，平衡后其表面温度与其余两相的温度必定相等，记为T。因此，可以得到如下热力学平衡条件：

TI=TII=TIII=T

(7-1)

(7-2)

其中(7-2)式从物理上可以理解为：平衡时，液滴表面呈球形，表面有收缩趋势，形成表面压强，与蒸汽压强二者之和应等于液滴内部的压强。

2 液滴蒸发温度与其半径之间的关系

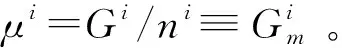
(8)

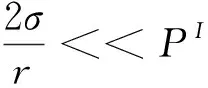
(9)

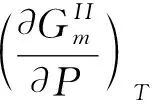
(10)

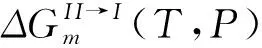
(11)

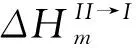
(12)

结合(10)和(12)式，可以得到：

(13)

进一步，

(14)

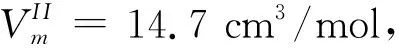
可见，当液滴半径接近纳米尺度时，其蒸发温度会明显下降。

从物理学来看，液滴比大块液体具有较低的蒸发温度是因为液滴具有额外的表面自由能，导致其具有较高的吉布斯自由能，这使得它比起大块液体显得更不稳定。因此半径越小的液滴越容易在较低的温度下蒸发，这与实际相一致。对上述关系式稍加修改，亦可以解释纳米材料领域的一个普遍现象：纳米颗粒材料的熔化温度也小于其块材熔化温度(熔点)，即将材料做成纳米尺度后，其熔融烧结温度将明显低于相应的固体大块材料[4]。一般解释为表面原子没有完全的成键，所以内聚能将明显降低。类比(14)，可写出下式：

(15)

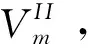
3 结论

在定压下条件下，将单元系的液滴和蒸汽两相共存的各相化学势看作每相对应的摩尔吉布斯自由能；同时，相对于蒸汽压强，当液滴表面张力引起的压强可被视为一级小量时，就可以得到液滴的蒸发温度与其半径的定量关系式。该关系式表明：半径越小的液滴越容易在较低的温度下蒸发。