考虑制造商公平关切的双渠道绿色供应链决策与协调研究

王苗苗，吴 军

(安徽农业大学 经济管理学院，安徽 合肥 230036)

近年来，如何在发展经济与低碳环保之间达到平衡，已经成为全球共同思考和探索的重要问题。作为实体经济的基础，制造业的绿色发展是实现我国经济高质量发展的前提，更是践行新发展理念、推动制造业高质量发展的重要举措。《中国制造2025》[1]行动纲领中更是提出要全面推行绿色制造。在绿色经济背景下，制造型企业纷纷开始绿色转型，进行绿色制造。

绿色供应链作为供应链管理的热点方向之一，受到国内外许多研究者的关注。Mohsin等[2]研究了基于绿色技术研发的绿色供应链微分博弈模型；Khorshidvand等[3]研究了包含绿色供应链协调和网络设计的混合模型；贺勇等[4]研究了政府补贴方式对绿色供应链制造商减排决策的影响机制；江世英等[5]构建了考虑产品绿色度的绿色供应链博弈模型，并设计了收益共享契约对供应链成员收益进行了协调与优化。程粟粟等[6]建立了绿色供应链微分博弈模型，通过动态批发价契约对绿色供应链成员进行了协调与优化。桑圣举等[7]研究了两级绿色供应链在不确定环境下的最优产品定价和绿色度决策问题。曹裕等[8]研究了绿色供应链的环境标签策略选择问题，并分析了成本分担契约对绿色供应链决策的影响。刘名武等[9]研究了关税、权力结构和消费者绿色偏好对绿色供应链决策的影响。上述文献虽然考虑了将绿色因素纳入供应链管理，但大多集中在单一渠道的供应链管理，没有考虑供应链中实际存在的双渠道结构。

目前学术界关于双渠道供应链的研究主要集中在渠道结构选择、产品定价决策、契约协调优化等方面。Ghosh等[10]分析了在消费者低碳偏好和政府碳配额与交易机制下的双渠道供应链的经济订货批量问题；Rahmani等[11]研究了双渠道供应链中产品绿色策略和定价的联合决策；杨茜等[12]研究了制造商主导下的不同渠道零售商的渠道选择和定价策略问题；黄红伟等[13]研究了考虑渠道商销售努力的双渠道供应链定价问题，并引入两部定价契约对供应链进行了协调；梁喜等[14]基于区块链技术和消费者敏感，研究了双渠道供应链的定价决策与渠道选择问题；孙红霞等[15]研究了双渠道零售商和传统零售商的定价决策问题；叶欣等[16]讨论了不同渠道结构下供应链成员的最优均衡策略；曹晓宁等[17]研究了考虑保鲜努力和新鲜度扰动需求的双渠道生鲜农产品供应链协调与优化问题。值得注意的是，上述研究的假设大多将双渠道供应链成员假设为完全理性，然而实际上供应链行为主体是有限理性而且自利的。因此，有必要将公平偏好理论引入到双渠道供应链管理的研究当中。

近年来大量研究表明，无论是制造商还是零售商都受到公平偏好的驱动，都可能会不惜放弃自己的边际收益达到更为公平的结果。Sharma等[18]研究了一个期权契约下两级供应链中渠道成员的公平关切问题；Sarkar等[19]研究了通过产品批发价契约协调闭环供应链存在的公平关切问题；杜少甫等[20]基于Nash讨价还价博弈模型，探讨了零售商的公平关切行为倾向对供应链的影响；邹清明等[21]分析了公平关切对渠道成员定价与利润的影响；曹柬等[22]研究了考虑零售商公平关切的闭环供应链动态决策优化问题。

结合上述文献可知，较少有学者将绿色供应链、供应链的双渠道结构以及供应链成员的公平关切行为结合起来研究的情形。本文综合考虑产品绿色制造、供应链双渠道结构、公平关切三方面因素，以单个制造商、线上线下渠道商和终端消费者组成的双渠道供应链为研究对象，探讨制造商的公平关切行为对决策变量以及供应链成员利润的影响，并为缓解制造商绿色制造成本压力，设计了两部定价契约对供应链进行了协调。最后，通过数值仿真实验对文章主要结论进行验证。

1 问题描述与符号说明

1.1 问题描述

本文考虑由单个制造商与线上线下两个渠道商组成的两级双渠道绿色供应链。上游制造商采用绿色低碳制造技术进行绿色制造，制造商进行绿色制造初期需要投入一定的绿色制造成本。在这个供应链中，制造商是Stackelberg博弈的领导者，其根据绿色制造投资成本以及生产成本确定绿色产品的批发价格与产品的绿色度；线上线下渠道商作为跟随者，以追求自身利益最大化作为决策准则，根据制造商确定的批发价格和产品绿色度制定产品零售价格，供应链结构如图1所示。

1.2 符号说明与研究假设

为便于描述，文中模型中所涉及的参数符号及其定义如表1所示。

图1 双渠道供应链结构示意图

表1 参数符号及其含义

研究假设：

(1)当绿色制造投资为一次性投资时，绿色制造成本系数k通常比较大，可合理假设k>2γ2；

(2)假设市场基本需求大于两倍的产品单位生产成本，即a>2c；

(4)假设消费者对线下渠道商的渠道偏好程度为μ(0≤μ≤1)，则对线上渠道商的渠道偏好程度为1-μ，μ越大说明消费者越倾向于通过线下渠道购买产品。整个市场对绿色产品的基础需求为a,从而线下和线上渠道商的产品实际需求分别为μa和(1-μ)a,进一步借鉴其他学者[19-20]所构建的需求函数可以得到以下关于线下和线上渠道商的需求函数表达式：

dt=μa-pt+γτ

(1)

do=(1-μ)a-po+γτ

(2)

(5)供应链实施两部定价契约以后，由于下游渠道商承担了部分绿色制造成本，所以假设制造商不再具有公平关切行为。

2 模型构建与求解

本节内容基于考虑产品绿色制造的双渠道供应链的运作框架，分别构建供应链集中决策模型与分散决策模型，并在分散决策模型的基础上进一步考虑制造商的公平关切行为。

2.1 集中决策模型

在集中决策模型中，可以将制造商、线上和线下渠道商三者看成一个集生产、线上线下销售为一体的企业，并以供应链总利润最大化为目标，整个供应链共同决定最优的线上线下渠道销售价格和产品绿色度。在此情形下，供应链总利润函数为：

(3)

(4)

(5)

(6)

将上述求解结果代入前文需求函数表达式(1)式和(2)式可得线上和线下渠道商的产品需求分别为：

(7)

(8)

(9)

2.2 制造商公平中性下分散决策模型

在分散决策模型下，制造商在决策中处于领导地位，线上线下渠道商都是跟随者，且均以追求自身利润最大化为目标。供应链成员的决策顺序为，制造商先确定产品的批发价格ω和产品绿色度τ，然后线上线下渠道商再根据批发价格和产品绿色度制定各自的零售价格po、pt。制造商、线上渠道商、线下渠道商各自的利润函数分别为：

(10)

(ω-po)(a(-1+μ)-γτ+po)

(11)

(12)

采用逆向归纳法对上述双渠道供应链模型分两阶段动态博弈进行求解，步骤如下：

(13)

(14)

(15)

(16)

将ωd、τd代入(13)(14)式，可得到线上线下渠道商最优零售价格为：

(17)

(18)

则相应的线上线下产品需求为：

(19)

(20)

制造商、线上和线下渠道商对应的利润分别为：

(21)

(22)

(23)

供应链总利润为：

4ack(-3k+γ2)+a2(γ4(1-2μ)2+

kγ2(-5-16(-1+μ)μ)+

k2(7+16(-1+μ)μ))

(24)

2.3 制造商公平关切下分散决策模型

绿色供应链生产过程中，制造商不仅独自承担产品的原始生产成本，而且为转型绿色制造还投资了大量一次性投资成本。因此制造商在供应链利润分配过程中将会更加注重利润分配的公平性。当制造商具有公平关切属性时，制造商决策时不再仅仅关注自身利润，而会更加关注自身的公平效用，制造商的决策目标将变为最大化自身公平效用Um。

对于制造商公平效用的刻画，本文借鉴杜少甫等[18]的处理方法，以供应链各方的纳什讨价还价解作为公平参考点，据此来刻画制造商对公平的感知。此种情况下可得到制造商和线上线下渠道商的效用函数分别为：

(25)

Uo=Πo

(26)

Ut=Πt

(27)

求解过程与上一小节类似，采用逆向归纳法求解该博弈过程。可得制造商公平关切下分散决策模型的均衡解为：

(28)

(29)

(30)

(31)

线上线下渠道商产品需求为：

(32)

(33)

供应链各成员利润分别为：

(34)

(35)

(36)

(8(a-2c)2k(-γ2+k(2+λ))+

(4ck+2aγ2(-1+2μ)+

ak(2+λ-2(4+λ)μ))2+

(4ck+a(-k(6+λ)+

2γ2(1-2μ)+2k(4+λ)μ))2)

(37)

上述定理表明，当制造商的公平关切系数变大时，制造商会提高批发价格，降低产品绿色度减少成本来预期提高自己的利润。当制造商提高批发价格时，线上线下渠道商也会提高他们各自的产品零售价格，由于产品零售价格上升和产品绿色度降低，绿色产品的需求量会大幅萎缩，价格提升的部分不能弥补需求减少的部分，从而导致制造商、线上线下渠道商的利润都下降，造成“多输”的局面，而这显然不利于整个供应链的运作。由此可见，制造商存在的公平关切行为对供应链上下游各个成员都不利。

2.4 均衡结果分析

通过对集中决策、分散决策和制造商公平关切下分散决策三种决策模型求解的均衡结果进行对比分析，可以得到以下命题：

证明首先，比较有无制造商公平关切下分散决策的线上线下渠道商产品零售价格。

命题2制造商公平关切下分散决策的产品绿色度依次小于公平中性下分散决策和集中决策情形，即τf<τd<τc。

命题3制造商公平关切下分散决策的产品批发价格高于公平中性下分散决策，即ωf>ωd。

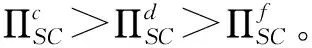
综合命题1到命题6可知，分散决策存在明显的“双重边际效应”，当制造商存在公平关切行为时，“双重边际效应”进一步加剧。

3 供应链实施两部定价契约

本节希望通过两部定价契约实现对产品绿色度、产品零售价格的同时协调，使得供应链总利润达到集中决策时的情形。在两部定价契约(ω,Ω)中，ω为制造商提供给线下线上渠道商的产品批发价格，Ω为线上线下渠道商向制造商支付的一笔固定报酬，假定线上线下渠道商向制造商支付的固定报酬相同，即都为Ω。则在两部定价契约下供应链各成员的利润函数为：

(38)

(39)

(40)

两部定价契约需要满足下列条件：

ω=c

(41)

将各均衡解代入各成员利润函数，根据不等式约束条件，可得Ω取值范围如式(42)所示：

(42)

定理2两部定价契约可以完全协调双渠道绿色供应链，供应链各成员利润高于分散决策情形，且供应链总利润等于集中决策情形。两部定价契约值为：(ω,Ω)，其中ω=c，Ω的具体取值由制造商和线上线下渠道商的谈判能力决定。

这里一个有趣的发现是，在两部定价契约下，当制造商把绿色产品以成本价批发给线上线下渠道商时(即当ω=c时)，线上线下渠道商如果各自向制造商支付一笔固定报酬，就能实现供应链的完全协调。

4 数值分析

为了更直观地呈现前文研究结论，本章将通过具体算例来解析。首先，对文中的基本参数进行了设定(表2)。

表2 参数设置

4.1 三种双渠道供应链决策模型的对比分析

将上述参数取值分别代入模型可得三种供应链决策情形的最优决策变量值和利润值(表3)，其中，制造商公平关切下分散决策的关切系数取值为0.8，计算结果保留到小数点后两位。

表3 集中决策、分散和公平关切分散决策下双渠道供应链最优决策的变量值和利润值

表3数据表明：与集中决策相比，分散决策存在明显的“双重边际效应”，而当制造商存在公平关切行为时，“双重边际效应”进一步加剧。

4.2 制造商公平关切系数对决策变量和利润值的影响

通过数值算例探讨制造商公平关切系数λ对决策变量、线上线下渠道商产品需求以及供应链成员利润的影响。

由图2可知，当制造商公平关切系数变大时，制造商会提高自己的批发价格，线上线下渠道商也会相应提高产品零售价格。

由图3可知，当制造商公平关切系数变大时，制造商会降低绿色研发努力水平，产品绿色度也随之降低。

图2 制造商公平关切系数λ对批发价格和零售价格的影响

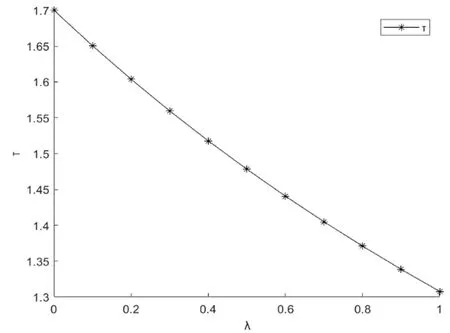
图3 制造商公平关切系数λ对产品绿色度τ的影响

图4 制造商公平关切系数λ对线上线下渠道商产品需求的影响

由图4可知，当制造商公平关切系数变大时，线上线下渠道商的产品需求都会萎缩。

图5 制造商公平关切系数λ对利润的影响

由图5可知，当制造商公平关切系数变大时，制造商利润、线上、线下渠道商利润都会随之降低。

综合图2—图5可知，当制造商存在公平关切行为并且公平关切系数逐渐变大时，制造商会降低产品绿色度并且提高批发价格，供应链下游的线上、线下渠道商作为回应，也会相应地提高产品零售价格。由于价格上升、产品绿色度降低，产品需求会萎缩，价格增加的部分不能弥补需求减少的部分，制造商利润、线上线下渠道商利润都会减少。由此可见，制造商存在的公平关切行为不仅会降低产品绿色度，不利于环境绩效的改善，也会损害供应链上下游成员的利润，不利于经济绩效的改善。

4.3 固定报酬Ω变化对供应链利润的影响

将表2的基本参数值代入两部定价契约，得到Ω的取值范围为2438.44<Ω<2648.81，具体Ω的值取决于制造商和下游线上线下渠道商的谈判能力。取值范围内分别取值验证两部定价契约的协调能力。

由表4可知，两部定价契约下供应链总利润等于集中决策情形，且制造商、线上线下零售商利润均高于分散决策情形，能够实现帕累托改进。所以两部定价契约可以完全协调供应链，这验证了定理2。

表4 Ω变化时供应链利润情况

5 结论

本文考虑了由制造商和线上线下渠道商组成的两级双渠道绿色供应链(即制造商进行绿色制造生产绿色产品并通过下游的线上线下渠道商向市场出售)，并分别在供应链集中决策、分散决策、制造商公平关切下分散决策三种模式下对绿色供应链进行建模分析，比较三种不同模式下产品绿色度、供应链成员定价、供应链成员利润以及供应链总利润的差异，探讨了制造商公平关切行为对供应链各成员决策以及利润的影响。最后，引入两部定价契约对供应链进行协调与优化，得到以下结论：

(1)与集中决策相比，供应链成员分散决策下存在明显的“双重边际效应”，线上线下零售商会提高零售价格，供应链总利润低于集中决策情形；

(2)当制造商存在公平关切行为时，分散决策下存在的“双重边际效应”进一步加剧；

(3)供应链实施两部定价契约可以完美协调供应链，完全消除“双重边际效应”，使供应链总利润达到集中决策情形，且供应链各成员利润都高于分散决策情形，能够实现帕累托改进。