雷达探测的理论极限

徐大专，张 晗，胡 超，潘 登

（南京航空航天大学电子信息工程学院，南京211106）

引 言

雷达探测的基本任务是目标检测和参数估计，通常首先进行目标检测，然后，根据检测到的目标存在状态信息进行参数估计。目标检测需要判断接收信号中是否有目标反射的回波，从而得出目标是否存在，确定目标个数［1］。通常的判断方法是将回波幅度与一个事先设定好的阈值进行比较，若回波幅度大于阈值，则说明目标存在，反之则说明目标不存在［2］。阈值的设定基于统计结果，因此存在判断错误的可能性。比如噪声的幅度超过了事先设定的门限，这种情况被称为虚警。在目标检测中，通常选用虚警概率-检测概率指标体系作为性能评价标准，即，给定虚警概率条件下，使检测概率最大化［3］。已经证明，在虚警概率-检测概率指标体系下，纽曼-皮尔逊（Neyman-Pearson，NP）准则是最佳的［4］。

在完成目标检测，判定有目标存在的情况下，需要对目标的距离、角度和速度等参数进行估计［5］。由于噪声和干扰的影响，每次参数估计都会存在误差，参数估计最重要的指标是估计精度［6］。最大似然（Maximum likelihood estimation，MLE）估计方法具有优越的性能，在实际中作为估计准则得到广泛应用。虽然最大似然准则是否最佳并没有得到理论证明，但在雷达信号处理中往往被看成事实上最佳，成为其他估计方法比较的依据。在多目标的情况下，MLE方法需要求解非线性的多维优化问题，为了减少密集多目标场景下的计算复杂度，一系列基于最大似然准则的算法被相继提出［7-9］，在取得接近MLE方法性能的前提下减少了运算量。若多个目标的分布具有稀疏特性，压缩感知（Compressed sensing，CS）类方法可以提高参数估计的性能或减小计算量［10-11］。

雷达目标检测和雷达参数估计的理论体系已经较为完善，但是对于联合目标检测-参数估计的研究较少。目前，联合目标检测-参数估计方法可以分为两类。第1类方法是分别处理这两个子问题，并在每种情况下使用相应的最优方法。比如，采用NP准则进行目标检测，然后，采用最优贝叶斯估计器进行参数估计，以解决组合问题。但Middleton等［12］指出，用最佳方案分别处理目标检测和参数估计并不一定会得到最佳的整体性能。第2类方法是使用广义似然比检验（Generalized likelihood ratio tests，GLRT）同时进行检测和估计［13］。Rezaeian等［14］通过在有限点的参数空间采样，将联合检测/估计问题简化为等效的多假设。但是当参数假设为连续值时，因为它们仅仅构成了对原始问题的近似，在有限样本的前提下，GLRT方法无法保证最优性。Moustakides［15］将估计子问题的贝叶斯公式与检测子问题的适当约束相结合，为联合检测/估计的建立开发了最优的一步和两步测试方案。上述工作存在的主要问题是，由于目标检测和参数估计的性能指标不同，需要指定目标检测和参数估计的联合代价函数，从而将联合目标检测-参数估计问题等效为一个优化问题。而联合代价函数的构造往往取决于特定的应用场景，并没有什么通用的准则。因此，雷达探测的理论极限问题一直没有解决。

香农信息论在雷达探测中的应用可以追溯到20世纪50年代，Woodward和Davies采用逆概率原理研究距离信息问题［16-18］，得到了恒模散射单目标的距离互信息与时带积、信噪比（Signal noise ratio，SNR）的近似关系。Woodward和Davies的研究仅针对雷达参数估计系统中目标的距离信息问题，没有涉及散射信息。1988年，Bell首先将互信息测度用于雷达系统的波形设计［19］，以目标冲激响应与接收信号之间互信息为测度，Bell证明了最佳波形设计对应于信道容量的最优功率注水解［20］，该结论与通信系统的最优功率分配问题相一致。在Bell的系统模型中，目标的距离信息隐含于冲激响应中。由于实际环境中目标位置是不断变化的，因此，自适应的波形设计方法显得尤为重要。Bell的工作针对目标检测问题提出，其模型并不区分不同的目标，因此，从本质上说，Bell的互信息测度本质上是空间信息中的散射信息，而没有涉及参数估计系统中更重要的距离信息问题。文献［21］根据信息理论准则和最小描述长度准则，提出了一种目标检测方法。该方法在决策过程中不需要主观判断，目标的数量由信息理论准则或最小描述长度准则的最小值确定。

针对参数估计，作者提出了雷达参数估计的空间信息概念［22］，将空间信息定义为接收信号与目标距离及散射的联合互信息，且通过理论推导得到了单目标/多目标距离信息和给定目标位置条件下散射信息的闭合表达式，将距离信息和散射信息纳入统一定义框架中。在2019年，作者进一步提出熵误差概念［23］，并用熵误差评价参数估计系统的性能［24］。最近，进一步得到距离信息和熵误差的闭合表达式［25-26］，指出熵误差是雷达参数估计的理论极限，并证明所提出的抽样后验概率估计方法可以逼近理论极限。

在目标检测领域，作者给出了检测信息的严格定义，并推导出目标匹配和非匹配条件下检测信息的理论公式［27］。进一步指出检测信息是雷达目标检测的理论极限，并证明，所提出的抽样后验概率检测方法可以逼近理论检测信息。

在本文中探测指的是目标检测与参数估计的联合。通过引入目标存在状态变量，建立了联合目标检测与参数估计的统一系统模型。提出探测信息、检测信息和估计信息的严格定义，并证明探测信息是目标检测信息与已知目标存在状态的估计信息之和，从理论上解决了探测信息的定量问题。提出探测器性能的评价指标体系，包括正向指标：探测信息和反向指标：熵误差。针对恒模散射目标统计模型，推导出目标存在状态与位置的联合后验分布。提出了抽样后验概率探测理论方法，并证明其后验熵等于理论后验熵。本文的主要贡献是证明了雷达定理，指出了探测器的理论极限，为各种雷达探测方法提供理论依据。

1 目标探测系统模型

设雷达发射波形是带宽为B/2的理想低通信号，即ψ(t)=sinc(Bt)。假设在观测区间内可能存在k个目标，那么，雷达接收的基带信号为

式中：vk∈{0，1}为第k个目标是否存在的整数变量，vk=1表示目标存在，vk=0表示目标不存在。sk为第k个目标的散射信号，τk为第k个目标产生的时延，w(t)为带宽为B/2的复加性高斯白噪声（Complex additive white Gaussian noise，CAWGN），其实部和虚部的功率谱密度均为N0/2。

假设信号能量几乎全部在观测区间内，根据Shannon-Nyquist采样定理，以速率B对接收信号进行采样，观测区间长度对应的采样时间为T，则总采样点数N=TB，称为时间带宽积。离散形式的接收信号为

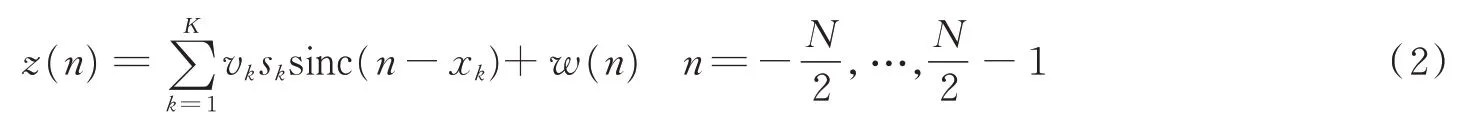
式中xk=Bτk表示归一化时延，各噪声样值之间相互独立，其实部和虚部也相互独立，噪声功率均为N0/2。

为了描述方便，将式（2）写成矢量形式

式中：s为散射系数矢量，w为噪声矢量。

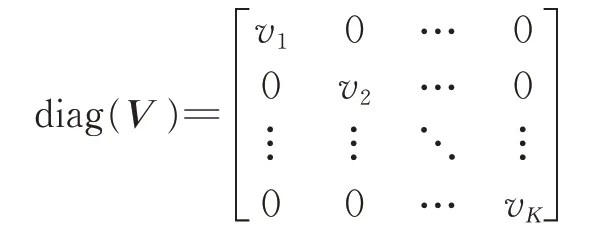
为目标存在状态矢量v=(v1，v2，…，vK)的对角化矩阵，U(x)=[…，u(xk)，…]称为目标位置矩阵，uT(xk)=(…，sinc(n-xk)，…)表示第k个目标的采样波形。式（3）是含有目标存在状态和参数的系统模型，称为探测系统模型，或探测方程，其主要特征是直接在系统模型中引入目标存在状态矢量。

上面的系统模型与普通目标检测系统具有明确的对应关系，即目标存在状态变量为0对应于假设检验H0，存在状态变量为1对应于假设检验H1。

2 探测信息、检测信息与估计信息

下面从统计观点处理系统方程。对接收端来说，目标存在变量和目标归一化时延及散射参数都是不确定的，令V表示目标是否存在的随机矢量，X和S分别表示目标的归一化时延矢量和散射矢量，W表示N维复高斯噪声矢量，其概率密度函数（Probability density function，PDF）为

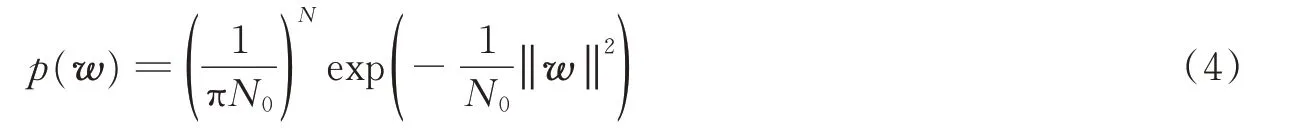
由探测方程，接收信号矢量Z是随机的。在给定存在状态矢量V，X和S时，Z的多维条件PDF为

式（5）的条件PDF定义了一个目标检测与参数估计的联合信道，由此可得如下探测信息的定义。

定义1探测信息：设目标检测矢量的先验PDF为π(V)，归一化时延的先验PDF为π(x)，散射信号的PDF为p(s)，那么，目标探测信息定义为接收信号与目标的存在状态、位置及散射的联合互信息，即

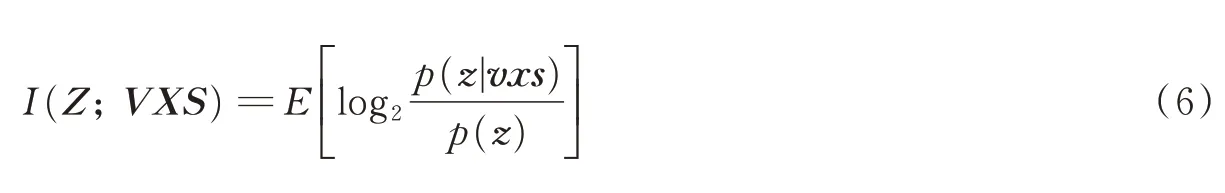
式（6）的互信息描述了接收信号含有的目标存在状态、位置及散射信息。类似地，接收信号与目标存在状态之间的互信息I(Z；V)称为检测信息，即

已知目标存在状态V条件下，接收信号与目标位置及散射之间的互信息I(Z；XS|V)称为估计信息，即

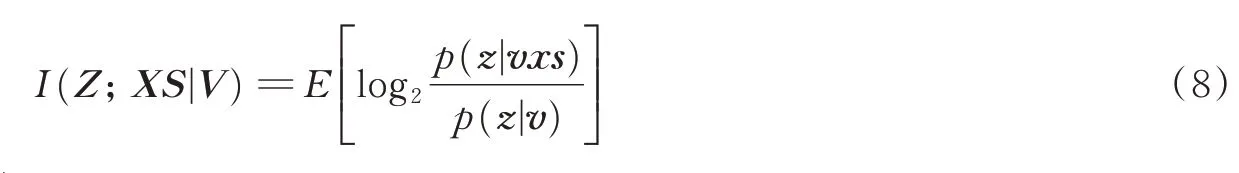
估计信息也称为空间信息。由于

则

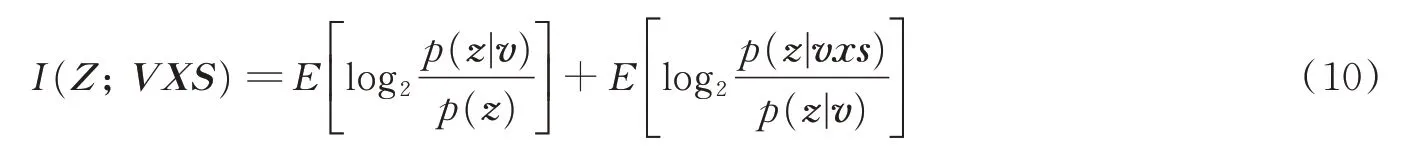
那么

式（11）表明探测信息是目标检测信息与已知目标存在状态条件下的空间信息之和。该式同时揭示了探测信息的获取方法，即，首先进行目标检测，所能获得的检测信息为I(Z；V)。在已知目标状态后再进行参数估计，所能获得的估计信息为I(Z；XS|V)。迄今，在雷达信号处理中目标检测和参数估计通常是分开处理的。在进行参数估计时通常默认已知目标数。探测信息的定义将目标检测与参数估计在信息论框架下统一起来，为雷达探测的信息获取问题提供一个总体描述框架。

3 雷达探测的性能指标

探测器的任务是进行目标检测和参数估计，也可说探测器由目标检测器和参数估计器两部分组成。那么，怎样对探测器的性能进行评价呢？目标检测器传统的评价方法是虚警概率-检测概率指标体系，参数估计的评价指标是均方误差，这两种评价指标很难纳入一个统一的指标体系中。针对参数估计器，作者提出了用后验微分熵或熵误差作为评论指标。针对目标检测器，作者提出用检测信息作为评价指标。这两种评价指标都是从信息论角度提出的，为检测器和估计器建立统一的评价体系铺平了道路。

3.1 探测信息

为了描述方便，下面考虑目标存在状态和目标位置的联合探测问题。对式（5）中散射信号求期望可得探测信道的条件概率分布p(z|v x)。不访设目标在观测区间上的先验分布为均匀分布，则由贝叶斯公式，已知接收信号的后验分布为

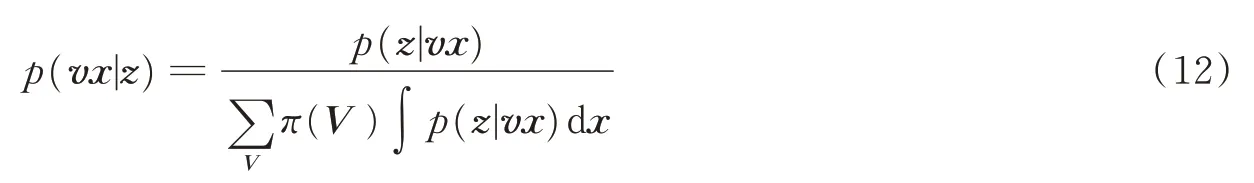
式中π(V)是目标存在状态的先验分布。

定义的探测信息是探测器从接收信号中所能获得的信息量，探测信息越大，探测器的性能越好。因此，探测信息可以作为探测器性能的评价指标。由式（11），得

式中：等号右边第1部分是检测器获得的检测信息，第2部分是已知目标存在状态条件下参数估计器获得的信息。这样，探测器获得的信息是检测器与估计器获得的信息之和，因此，探测器、检测器和估计器的性能可以由所获取的信息量进行统一评价。

3.2 后验熵

另一种方法是用不确定性评价探测器的性能，这是一种反向指标，不确定性越小，性能越好。由定义

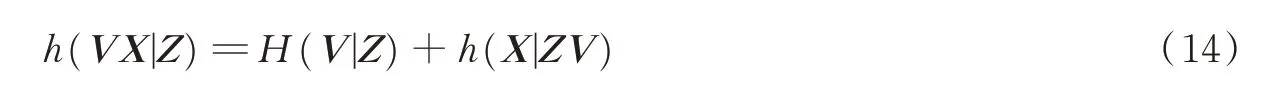
式中：h(XV|Z)为探测器的后验熵，表示探测器的总体不确定性；H(V|Z)为检测器的后验熵；h(X|ZV)为已知目标存在状态条件下估计器的后验微分熵。探测器的后验熵等于检测器与估计器的后验熵之和。

3.3 熵误差和熵偏差

探测信息和后验熵都是相对性指标，作为性能评价指标的不足之处是不够直观。为此，本文采用后验熵的熵幂作为探测器的性能指标，熵幂在很多文献中也称熵功率。

3.3.1 探测器的熵误差和熵偏差

探测器熵误差的定义类似于估计器，有

定义2探测器的熵误差定义为其后验熵的熵幂，即。

由后验熵公式

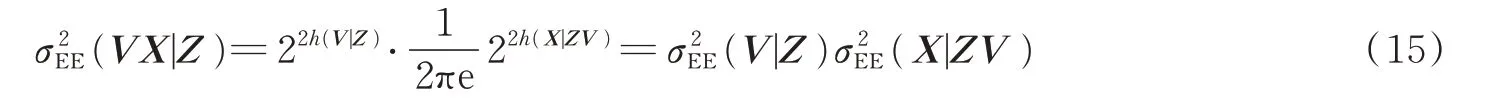
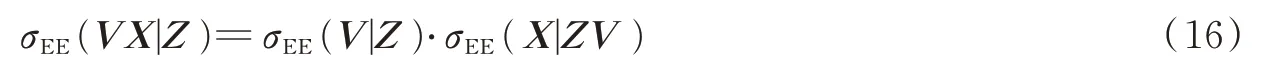
式中σEE(V|Z)=2h(V|Z)和分别为目标检测器的熵偏差和参数估计器的熵偏差。可见，探测器的熵偏差也是目标检测器的熵偏差和参数估计器的熵偏差之积。

3.3.2 目标存在状态的熵数

目标存在状态是离散信源，其熵偏差是一个新的概念。为了分析离散信源熵偏差的物理意义，针对一般离散信源，有

定义3离散信源V的熵数定义为NH=2H(V)，其中H(V)是信源的熵。

算例1n元等概率信源的熵数NH=n。

因为等概信源的熵为log2n，故其熵数为n。

算例2n元确定性信源的熵数NH=1。

因为确定性信源的熵为零，故其熵数为1。

算例3信源V∈{1，2，3，…}的概率分布为，其熵数NH=4。

该信源的熵H(V)=2，故熵数为NH=4。

上面3例表明，熵幂表示离散信源中元素的有效个数，概率分布越均匀，熵数越大，概率分布差异越大，则熵数越小。一般1≤NH≤Card，这里Card表示集合中元素的个数，即基数（Cardinal）。算例3的信源有无穷多个元素，基数无穷大，但是，由于概率分布不均匀，其熵数为有限值。

在目标检测中定义检测器的熵偏差为其后验熵的熵数。熵数越小，表明检测器的性能越好。如果熵偏差为1，则表明不存在任何不确定性。

参数估计器熵误差和熵偏差的定义与文献［25］是一致的，熵误差是均方误差的推广，在高信噪比时退化为均方误差。

4 恒模散射目标探测器、检测器和估计器的性能

恒模散射模型是一种典型的非起伏目标散射模型，又称Swerling0模型，这时复散射系数的模为常数，相位在[0，2π]内均匀分布。多目标恒模散射信息的计算十分复杂，下面只考虑单目标情况。

4.1 恒模散射目标探测器的性能

令复散射系数s=αejφ，这里α表示散射系数的模，φ表示散射系统的相位。将s=αejφ代入式（5），则条件概率分布为

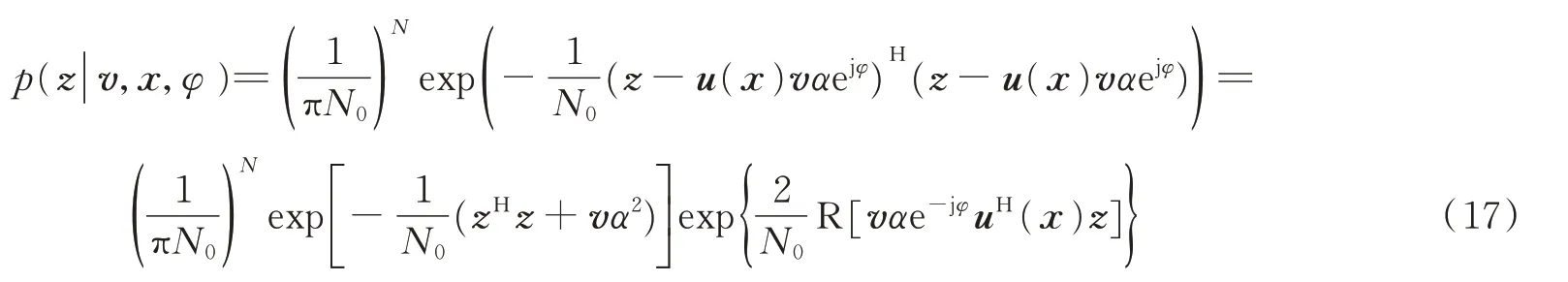
由于模为常数，所以α没有出现在左边的条件变量中。对随机相位求期望得

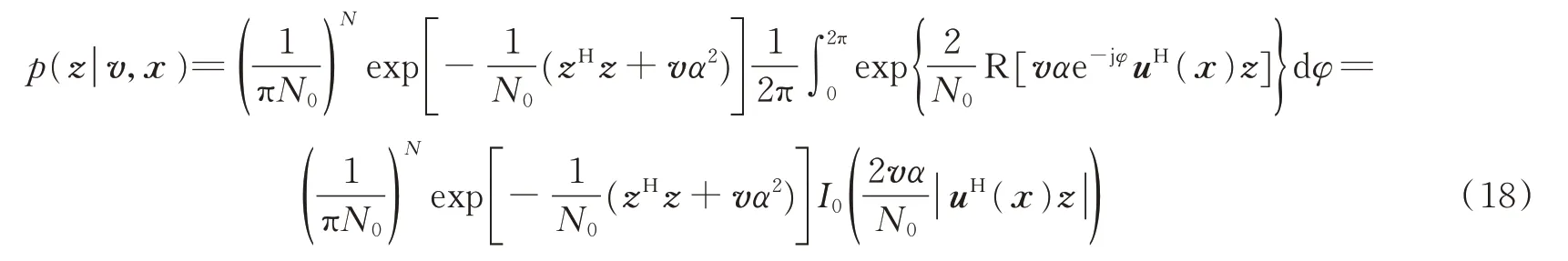
式中

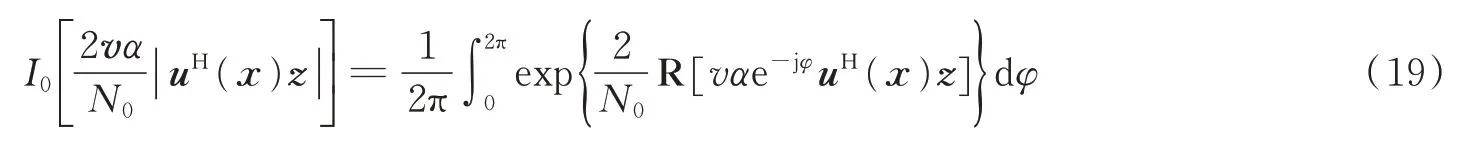
式中：I0[·]表示第一类零阶修正贝塞尔函数，R[·]表示取实部。式（18）条件概率分布刻画了一个探测信道，其输入是目标的存在状态和归一化时延(v，x)，信道的输出是接收信号。已知接收信号时，式（19）是(v，x)的似然函数。

接收信号中含有目标存在状态和位置信息，由贝叶斯公式得后验PDF为

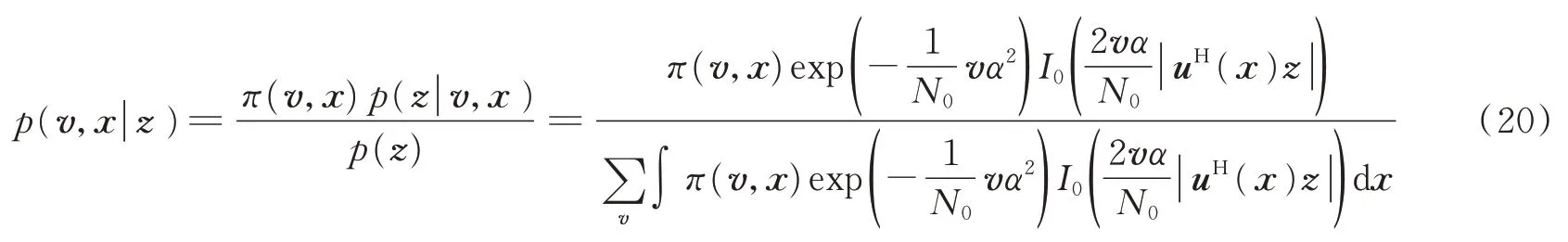
式中π(v，x)表示目标存在状态和位置的联合先验分布。通常目标的先验状态和位置是互不相关的，即π(v，x)=π(v)π(x)。式（20）中uH(x)z表示匹配滤波器的输出。由后验概率分布，根据式（15）可以计算后验熵h(V，X|Z)和熵误差。

为了进一步说明后验熵与目标存在状态和位置的关系，假设目标实际状态为(v0，x0)，则接收数据

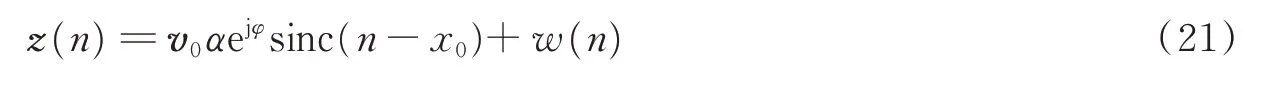
由(v0，x0)产生的接收数据记为z(v0，x0)，则匹配滤波器输出

式中

是由N个噪声样本内插得到的噪声信号。由于散射信号的相位对取模运算没有影响，代入式（21）得

式中：ρ2=α2/N0表示信噪比，它是散射信号能量与总噪声功率之比；w(x)/α为均值为零、方差为1/ρ2的复高斯噪声。

式（24）表明，目标位置的后验分布是以实际目标位置为中心的对称分布。目标位置改变将使后验分布产生平移，但不改变分布的形状。另外，后验分布不仅取决于目标状态(v0，x0)，还噪声样本有关。

一般的雷达探测系统由探测信道和探测器两部分组成，如图1所示。探测信道由式（18）的条件PDF所刻画，取决于雷达系统参数和噪声的统计特性。探测器从接收信号中获得目标存在状态和位置的推断，通常需要利用目标的先验统计特性。

图1 雷达探测系统Fig.1 Radar system

根据最大似然准则和最大后验概率准则，使后验概率分布p(v，x|z(v0，x0))达到最大的称为目标状态(v0，x0)的最大似然探测，记为，即

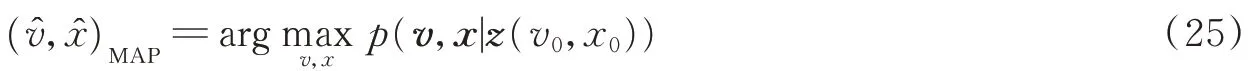
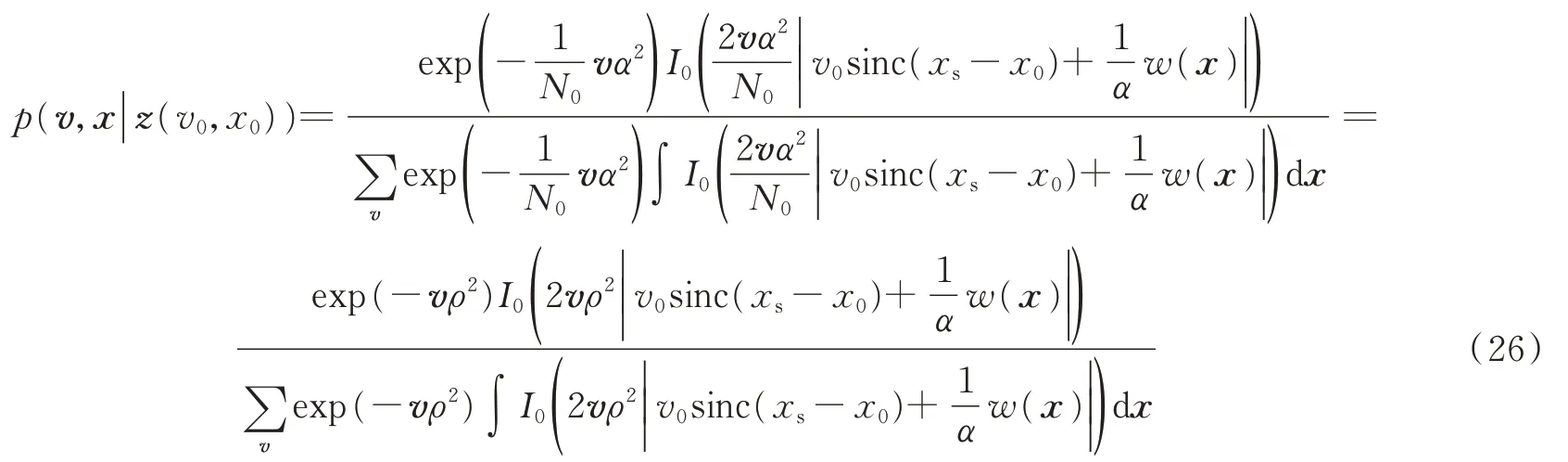
式（26）的分母是归一化常数，后验分布的形状完全取决于分子的似然函数。

使似然函数p(z|v，x)达到最大的称为目标状态(v0，x0)的最大似然探测，记为，即

对后验概率分布p(v，x|z(v0，x0))进行抽样产生的推断称为(v0，x0)的抽样后验概率（Sampling a posteriori probability，SAP）探测，记为，即

SAP探测器是一种随机检测器，给定接收信号时探测结果是不确定的，其平均性能取决于后验概率分布p(v，x|z)。由式（25），给定目标(v0，x0)时，SAP探测器的后验PDF为

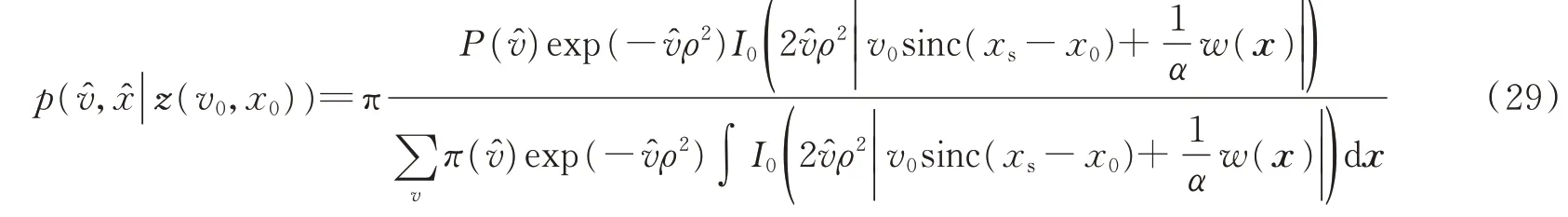
式（29）也可以表示为

即后验PDF既是目标状态(v0，x0)的函数，也与噪声样本有关。如果用表示给定噪声样本时的后验熵，即

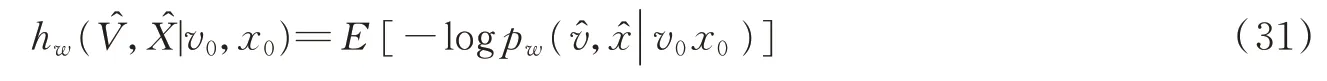
那么，给定目标状态(v0，x0)时，SAP探测器的后验熵为

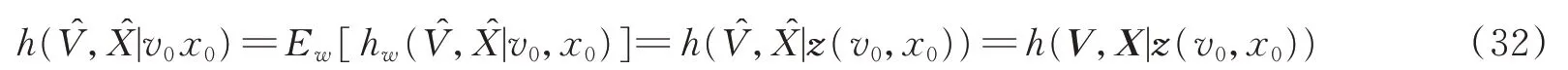
式（32）表明，给定目标状态(v0，x0)时，SAP探测器的后验熵就是理论后验微分熵h(V，X|z(v0，x0))。那么，在无任何先验信息情况下，SAP探测器的探测信息

即SAP探测器的探测信息等于理论探测信息。

4.2 恒模散射目标检测器的性能

在观测区间内对目标位置求期望得

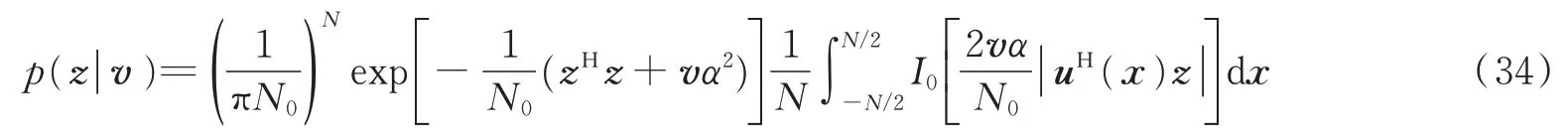
再由贝叶斯公式得后验分布为

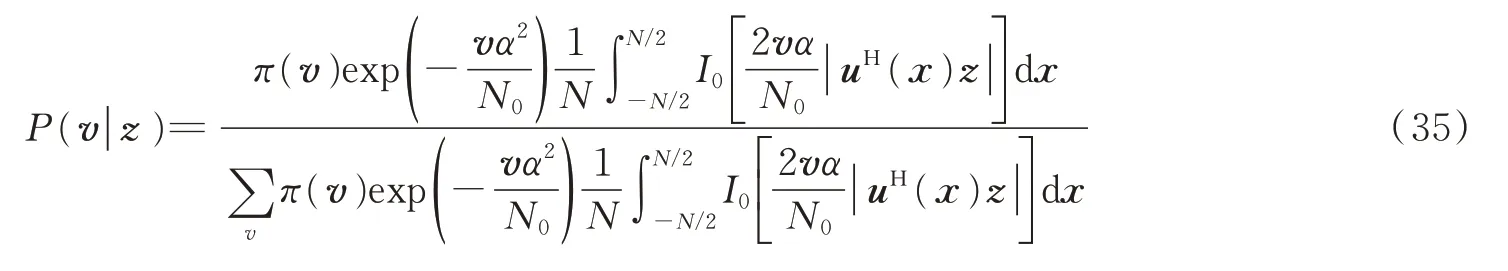
或

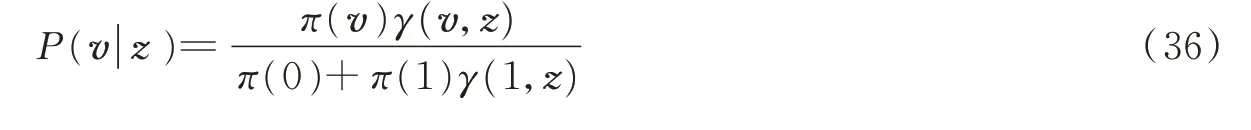
式中

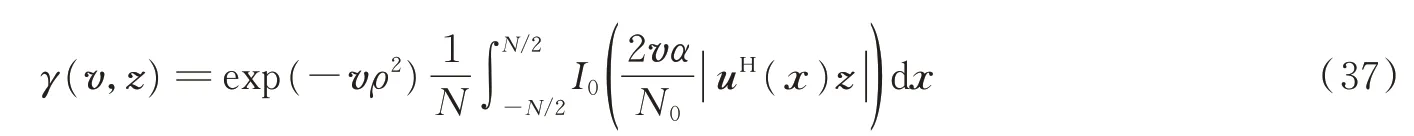
表示恒模散射目标的检测统计量。注意到|zHu(x)|为匹配滤波器输出的模值，γ(v，z)为|zHu(x)|的贝塞尔函数在观测区间内的时间平均。显然，γ(v，z)与普通的能量检测器不同，也就是说，已知目标散射和信道的统计特性后，能量检测器并不是最佳检测器。

由后验概率分布，根据式（37）可以计算检测器的后验熵、熵误差和熵数。式（37）是从信息论角度推导出的后验概率分布，代表检测器所能达到的理论极限，与检测器的具体结构以及检测方法无关。

最大后验概率（Maximum a posteriori probability，MAP）检测器选择后验概率最大的目标存在状态作为检测器输出，即

对后验概率分布P(v|z)进行抽样产生的估计v^称为目标存在状态的抽样后验概率检测，记为，即

4.3 恒模散射目标参数估计器的性能

由探测信道的条件概率分布，已知接收信号和目标存在状态时的后验概率分布为

显然，当目标不存在时，式（40）退化为均匀分布。当目标存在时，该后验分布与文献［25］一致。由后验分布可以计算估计器的估计信息和熵误差。

5 雷达探测的理论极限

本节的目的是证明前面提出的探测信息和熵误差是雷达探测的理论极限。在证明定理之前，首先描述需要用到的几个概念。

目标信源是指定义在目标存在状态集N={0，1}和观测区间R上的随机矢量Γ=(V，X)∈N×R，γ=(v，x)是Γ的一个样本，简记为γ=vx。在获得接收信号之前，目标存在状态和归一化时延是相互独立的，故p(v，x)=P(v)p(x)，且时延的先验分布为均匀分布。

m次无记忆扩展目标信源指扩展目标信源Γm之间相互独立，m次无记忆扩展目标信源记为Γm=(Vm，Xm)∈Nm×Rm。由图1，探测信道是从目标信源空间N×R到N维复数空间CN的条件概率分布p(z|v，x)，其输入是目标信源矢量γ=(v，x)，输出是接收信号矢量z。

无记忆扩展信道（Memeryless snapshot channel，MSC）指多次独立快拍产生的扩展信道满足

上面的探测器对目标检测与参数估计进行联合探测，故称联合探测器。给定目标信源和探测信道时，下面定义探测器的经验熵和经验探测信息。

图2 m次快拍探测系统Fig.2 Radar systems of m snapshots

定义4探测器从M次快拍得到的经验熵定义为，经验熵误差定义为，经验熵偏差定义为，经验探测信息定义为。

定义5可达性：理论熵误差称为可达的，如果存在一个探测器，其M次快拍的经验熵误差满足

定义6ε-联合典型序列：服从联合分布p(γ，z)的ε-联合典型序列集是M长序列对集合{(γM，zM)}的子集，其经验熵与理论熵之差小于ε，即

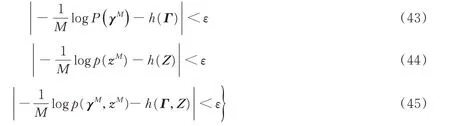
式中

引理1对于无记忆快拍信道p(zM|γM)，如果是后验概率分布p(γ|z)的M次独立抽样，则是关于概率分布的联合典型序列。

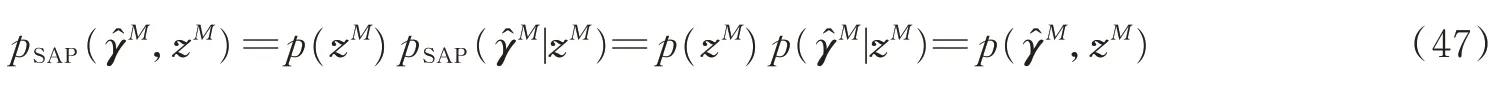
证毕。

由引理1和联合典型序列的定义，立即有

定理1雷达定理：理论熵误差是可达的，具体来说，设探测器已知目标信源和探测信道的统计特性，则，对任意ε＞0，存在探测器的经验熵误差满足

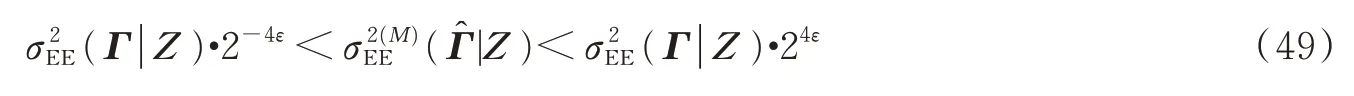
且

反之，不存在经验熵误差小于理论熵误差的任何探测器。

定理分为正定理和逆定理两部分，先证明正定理。

正定理的证明：

首先根据目标先验分布独立产生M次扩展目标信源样本γM，再根据γM和M次扩展信道p(zM|γM)产生接收序列zM，则接收信号zM满足

根据联合典型序列的定义，对任意ε＞0，只要快拍数足够大，有

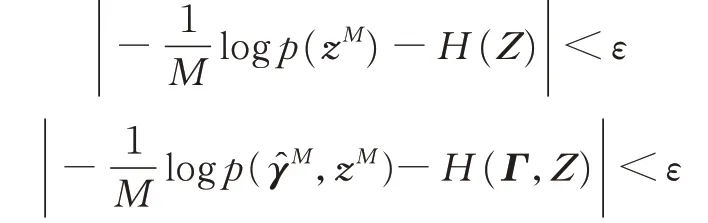
或写成

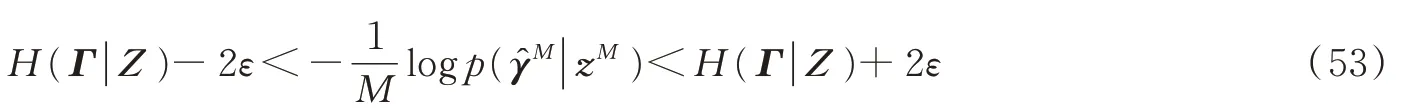
根据经验熵误差的定义

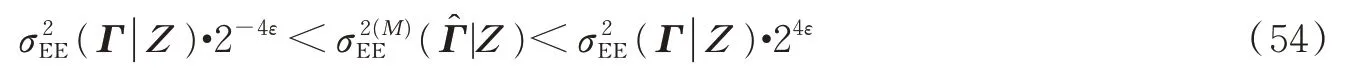
再由契比雪夫定理，随快拍数M→∞，ε→0，则

逆定理的证明：

则经验后验熵

由于经验熵与经验熵误差一对对应，那么，任何探测器的经验熵误差不小于理论熵误差，证毕。

探测定理指出，探测熵误差是探测器的理论极限，并且，抽样后验探测器的性能可以逼近理论极限。雷达定理提供了一个证明框架，虽然证明过程针对单目标情况，但证明方法也可以推广到多目标情况。

作者在文献［25］中证明了参数估计定理，文献［27］中证明了目标检测定理。如果将探测过程分为目标检测与参数估计两个阶段，如图3所示。第1阶段，检测器根据接收信号获得的目标存在状态信息；第2阶段，估计器根据检测结果和接收信号估计目标位置。那么，这种检测器与估计器级连的探测方法能否达到雷达探测的理论极限呢？由抽样后验检测器与估计器级联的目标探测系统如图3所示，级联系统的一次探测过程由目标信源、探测信道、检测器和估计器及部分组成，图3表明了检测器将检测的结果传递给估计器进行参数估计。

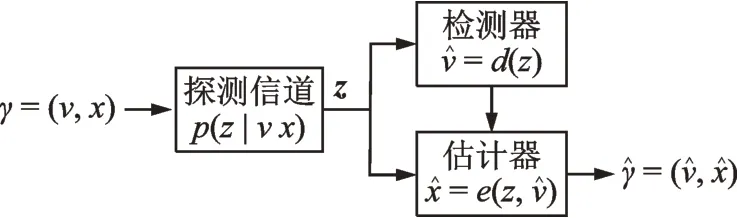
图3 目标检测与参数估计级联的雷达探测系统Fig.3 Radar systems concatenating target detector and parameter estimator

定理2目标检测与参数估计分离定理：随快拍数增加，抽样后验检测器的经验检测信息与抽样后验概率估计器的经验估计信息之和可以逼近探测信息的理论极限。

证明：由探测信息的可加性

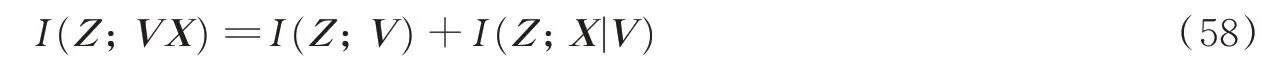
由目标检测定理，抽样后验检测器的经验检测信息可以逼近理论极限I(Z；V)。而

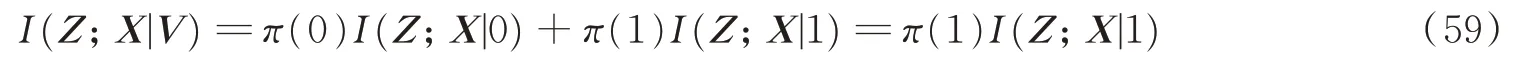
式中I(Z；X|1)是已知目标存在时的位置估计信息。由参数估计定理，抽样后验概率估计器的经验估计信息可以逼近理论极限I(Z；X|1)。故，由抽样后验检测器和抽样后验概率估计器级连组成的探测系统可以逼近探测信息的理论极限I(Z；VX)。证毕。

6 数值仿真结果与分析

分别对探测器性能以及目标检测与参数估计分离定理进行仿真验证，设定雷达探测的时间带宽积TB=128，仿真次数为10 000次。

6.1 探测器性能的数值仿真结果与分析

探测信息的数值仿真结果如图4所示，熵偏差的数值仿真结果如图5所示。可以看出，SAP探测器的经验检测信息、经验估计信息和经验探测信息均逼近理论结果，另外，SAP探测器的经验熵偏差也均逼近理论值，从而验证了雷达定理证明的结论。

图4 SAP探测器的经验信息与理论信息Fig.4 Empirical information of SAP detector and theoretical information

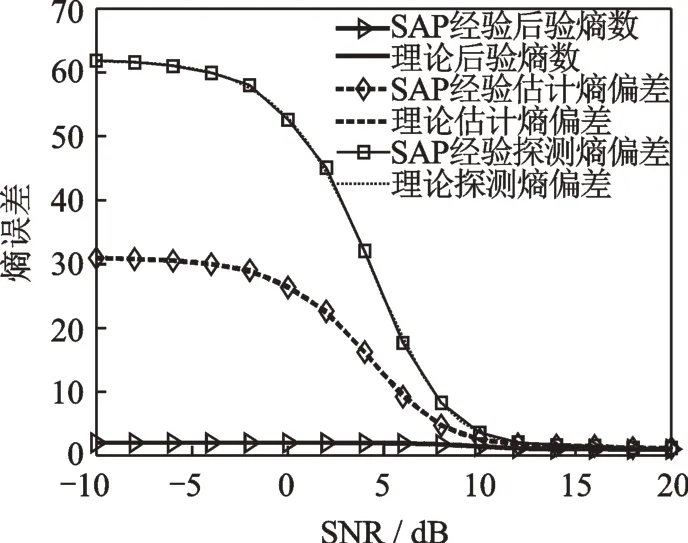
图5 SAP探测器的经验熵偏差与理论熵偏差Fig.5 Empirical entropy deviation of SAP detector and theoretical entropy deviation

6.2 目标检测与参数估计分离定理的验证

对目标检测与参数估计分离定理进行数值仿真验证。联合探测系统与级联探测系统的理论探测信息如图6所示，结果表明，探测信息是检测信息与估计信息之和。

SAP联合探测器与SAP级联探测器的经验探测信息的比较如图7所示。可以看出，两种探测器获得的探测信息是一致的，验证了目标检测与参数估计分离定理的正确性。

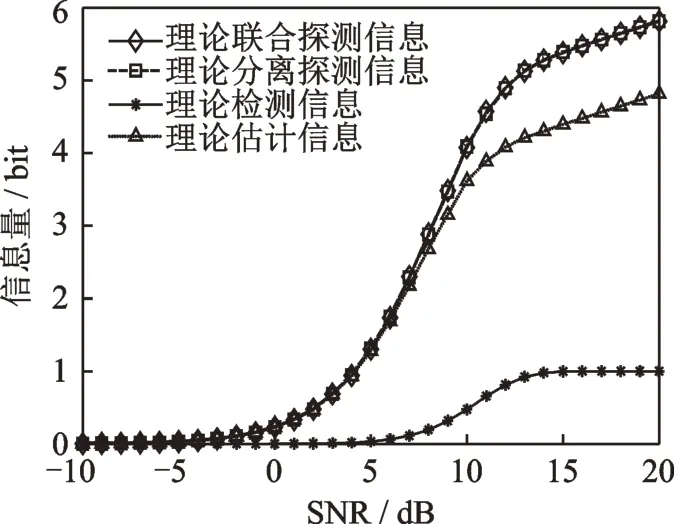
图6 联合探测器与级联探测器的理论探测信息Fig.6 Theoretical radar information of joint and concatenated target detector and parameter estimator

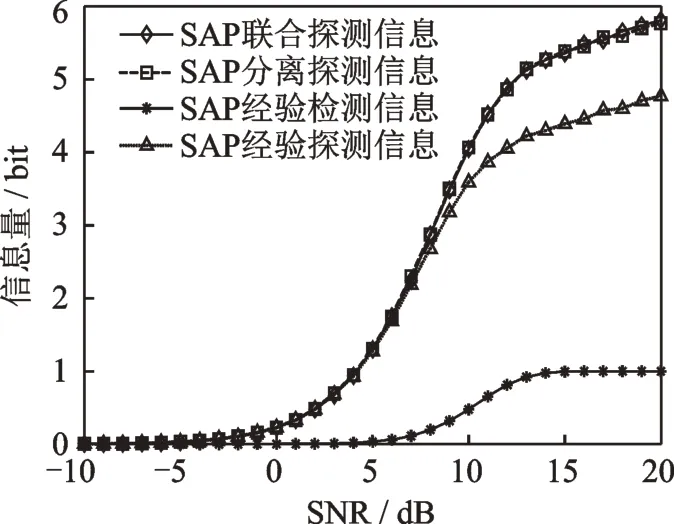
图7 SAP联合探测器与级联探测器的经验探测信息Fig.7 Empirical SAP radar information of joint and concatenated target detector and parameter estimator

值得注意的是，目标检测器不仅输出目标存在的状态，还要同时给出对应状态的概率，相当于通信系统中解调器的软判决，总的估计信息需要用存在状态的概率进行加权。

7 结束语

在雷达信号处理中，目标检测和参数估计通常是先后进行的两个处理过程。本文建立了结合目标检测与参数估计的统一系统模型，并提出抽样后验探测理论方法。本文的主要贡献是，指出了探测信息和探测熵误差是雷达探测的理论极限，并证明，抽样后验概率探测器可以逼近雷达探测的理论极限。雷达定理和分离定理从理论上回答了最优雷达探测问题，将对雷达探测技术发展产生巨大推动作用。