基于QoE感知的星地一体化网络公平资源分配策略

曾骏杰，李丽楠，辛 宁，李久超，张 磊

（1.中国空间技术研究院通信与导航卫星总体部，北京100094；2.国家航天局卫星通信系统创新中心，北京100094）

引 言

随着互联网的广泛普及和移动通信技术的飞速发展，多媒体、流媒体等高数据应用业务已成为未来无线通信系统的主导。因此，随着无线数据业务需求的爆炸式增长，为用户提供良好的数据服务体验成为未来无线网络面临的重大挑战。星地一体化网络可以有效融合卫星网络和地面网络优势，实现全球无缝覆盖，在提供通信广度的同时，有效提升频谱利用效率［1-2］。然而，要有效满足用户业务服务体验，高效管理一体化网络资源，星地一体化网络在无线管理方面还面临着诸多挑战。随着数据业务类型的多样化和频谱资源的稀缺性，用户数据服务体验质量（Quality of experience，QoE）和服务公平性已成为未来网络资源分配的重要指标。由于无线信道条件的时变性和用户业务的多样性，星地一体化网络迫切需要探索更加高效、自适应的动态资源分配机制，以满足移动用户多样化的服务体验需求。

目前星地一体化网络资源管理方面已经有了一些研究成果［3-10］。但是这些成果往往着眼于优化网络能耗［5-7］和降低网络干扰［8-10］等方面，优化目标过于单一，并没有将用户服务体验和用户服务体验公平性纳入考虑。为了提高用户服务体验，当前学者针对地面无线网络的QoE或公平性资源分配优化方面做了大量的工作［11-15］。为了实现用户满意度的公平性，Meng等提出了一种基于冲突图的正交频分多址（Orthogonal frequency division multiple access，OFDMA）家庭基站网络SMALL CIR算法［11］。Ha等提出了一种分布式低复杂度算法，通过考虑用户的公平性来解决联合子信道分配和功率控制问题［12］。为了满足服务的最小QoS要求并获得均衡的公平资源分配，Long等提出了一种公平的QoS感知资源分配方案，该方案综合考虑了信道分配、多径路由、链路调度和无线分配等因素，解决了交叉层优化问题［13］。Wang等提出了一个超公平动态ICIC框架，该框架可以在不明显降低系统频谱效率或增加计算复杂度的情况下实现最大化公平性［14］。然而，上述文献都集中在静态无线信道条件下的瞬时资源分配上，没有考虑动态无线信道条件的波动。针对动态时变网络，当前广泛利用李雅普诺夫优化理论（Lyapunov optimization theory）对时变信道下的QoE性能进行研究［16-18］。其中，Guo等设计了一种针对OFDMA网络的资源管理方案，该方案同时考虑了时变信道和用户的个性化服务需求［16-17］。Guo等利用峰值信噪比（Peak signal to noise ratio，PSNR）来评估用户的QoE需求，并提出了一种联合速率控制和资源分配方案，以最大化所有用户的时间平均QoE［18］。然而，以上公平性资源分配研究均着眼于地面网络，并没有将星地一体化网络场景纳入考虑。同时，上述研究仅仅着眼于优化系统的整体长时QoE性能，并没有将动态网络中用户多样化的QoE需求、公平性和时变信道条件综合纳入考虑。

为解决以上问题，本文将星地一体化网络的网络动态性、业务多样性和服务体验公平性综合纳入考虑，针对时变星地一体化网络，提出了一种基于QoE感知的公平资源分配策略。本文的贡献主要包括以下几点：

（1）利用平均目标分数（Mean objective scores，MOS）模型来评估用户的服务体验质量满意度，并引入公平效用方程，将优化问题描述为基于长时QoE的网络公平效用的最大化优化问题，从而实现公平地提高用户的时间平均QoE的优化目标。

（2）由于建模问题为复杂的动态优化问题，基于李雅普诺夫优化理论，引入辅助变量，将原问题从时间平均函数形式转化为只涉及时间平均的修正形式，并将问题分解为辅助变量选择、速率控制和资源分配3个子问题。同时，对于非凸混合组合优化的资源分配子问题，提出了一种求解资源分配子问题的低复杂度两步算法来进行有效求解。

（3）构建仿真平台验证方案性能，仿真结果揭示了所提出的资源优化策略在不同的公平性参数下用户的长时QoE与公平性之间的折衷性能。

1 系统模型

考虑同层干扰下行星地一体化网络，如图1所示。为了方便表示和描述，将卫星和地面基站统称为基站。假设网络具有S个基站、U个活跃用户和N子信道，令S={1，…，S}，U={1，…，U}分别表示所有基站和用户的集合，其中，1号基站设定为卫星，其他基站为地面基站。其中，用Us表示接入基站s的用户集。假设每个用户在一个给定的时隙只能接入一个基站，每个用户都有一个视频流服务。所有基站共享相同的频谱带宽，这些带宽被划分成N个子信道，子信道集合表示为N={1，…，N}。因此，应该考虑星地一体化网络用户之间严重的同层干扰。网络以时隙方式进行数据传输，时隙t∈{1，2，…}。每个基站为每个服务用户维护一个传输队列，以存储需要传输的数据。在每个时隙开始时，假设网络中存在一个中央控制器，它可以获取系统的信道状态信息和队列状态信息，并负责在每个时隙进行速率控制和资源分配决策。

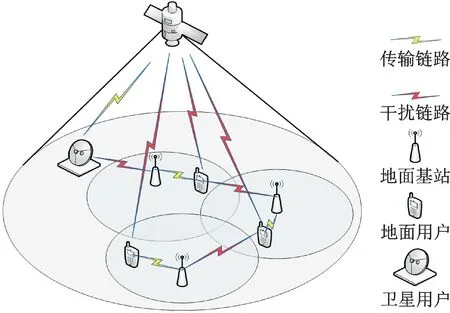
图1 系统模型Fig.1 System model

令ws，u，n(t)表 示 星 地 一 体 化 网 络 的 子 信 道 分 配 指 示 符。其 中，ws，u，n(t)=1表 示 子 信 道 在 时 隙t处分配给基站s中的用户u，否则，ws，u，n(t)=0。每个时隙子信道上基站用户的信干噪比（Signal to interference plus noise ratio，SINR）可以表示为

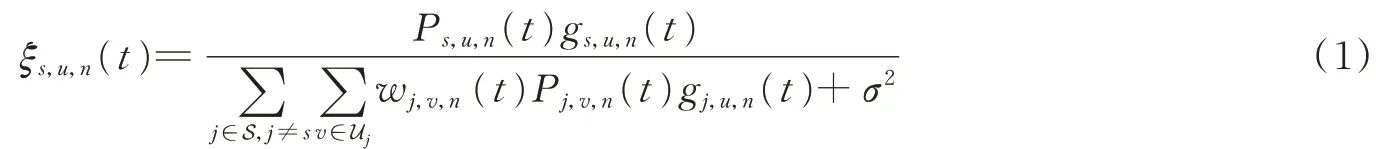
式中：Ps，u，n(t)为在子信道n上分配给基站s中的用户u的发射功率，gs，u，n(t)表示子信道n上基站s和用户u之间的信道增益，σ2表示每个子信道上的热噪声功率。基于香农公式，在第t个时隙接入基站s的用户u在子信道n上的传输速率可表示为

因此，用户在第t个时隙从基站s可获得的总传输速率可以写成

1.1 队列模型

令Qs，u(t)表示第t个时隙基站s中为用户u缓冲的数据的队列长度。Rs，u(t)和Cs，u(t)分别表示用户u在时隙t队列的到达数据和传输速率。用户的队列动态为

定义1如果满足式（5），则离散时间队列Qs，u(t)是平均速率稳定的［19］。

1.2 QoE模型

本文采用连续MOS模型来描述不同类型数据业务的QoE性能，而MOS模型可以用有界对数函数来表示。与长时时间平均吞吐量相对应的用户u的QoE可定义为

式中：QoE的取值在1到4.5之间，代表用户对服务质量的体验从差到优；a和b的参数取值取决于每个用户的最小数据需求和特定满意度需求。

根据文献［16，20］，a和b的取值可通过所需的最小数据速率和建议的数据速率将其进行参数化，具体可以表示为

2 问题描述

在这里，定义长时时间平均的QoE公平效用函数，并将优化问题描述为一个服从队列稳定性的随机优化问题。令φ(·)是一个凸的、连续的、非递减的网络公平效用函数，则优化问题可表述为

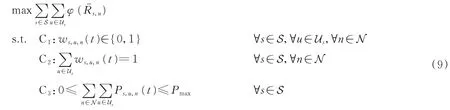
C4：所有队列Qs，u(t)为平均速率稳定的

式中：φ(·)为包含φ(·)和QoE(·)的函数，具体可表示为；C1和C2表示每个时隙的每个子信道在每个基站中最多只能被一个用户占用；C3为每个基站的功率约束，其中Pmax为基站的最大发射功率；C4为网络稳定性约束，以确保每个队列具有有限的队列长度。在本文中，考虑α-公平效用函数，其定义为

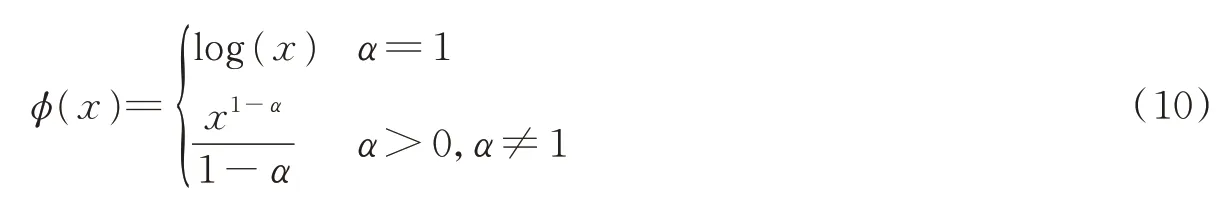
α的取值可以控制QoE和公平性之间的折衷，取值范围从0到∞。特别需要指出的是，现有文献中广泛使用的3种特殊情况，包括α=0，α=1和α=∞，分别对应于QoE总和最大化、比例公平和最大-最小公平这3种公平性表达模型。

定理1对于给定的α，复合函数φ(·)是凸的。

证明首先介绍引理1［21］。

引理1对于复合函数f(x)=h(g(x))，如果g是凸函数，且h是非递减的凸函数，则f是凸函数。

3 基于QoE感知的公平资源分配算法

由于原始优化问题中涉及时间平均变量的函数形式，而李雅普诺夫优化理论中的漂移加惩罚算法无法直接求解［16］。在这里，通过引入辅助变量的方式将包含时间平均变量函数的原始问题转化为只包含时间平均变量的优化问题。令{γs，u(t)}为第t个时隙的辅助变量，可以将问题转换为

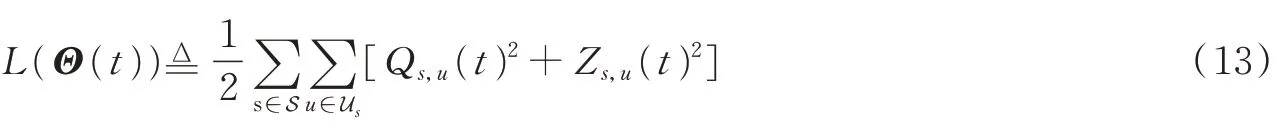
漂移加惩罚可以表示为

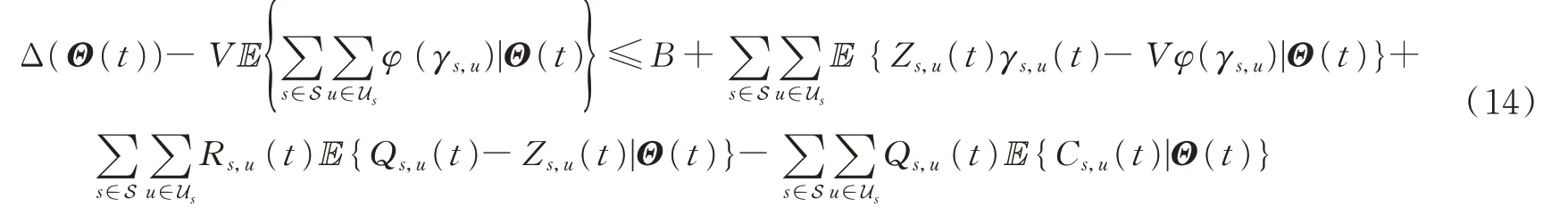
式中B为常数且满足以下条件

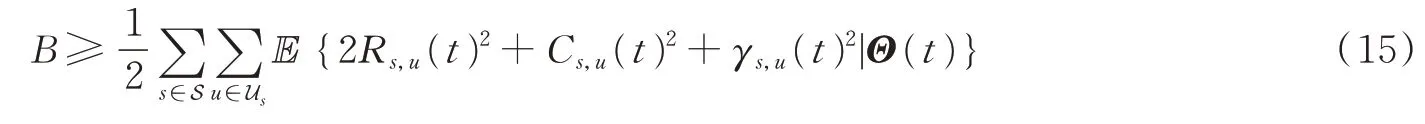
为了最小化式（14）的右侧部分，观察每个时隙的队列状态Z(t)，Q(t)，并将优化问题分解为3个可以独立求解的瞬时子问题。在这里，提出了基于QoE感知的公平资源分配算法来进行{γs，u(t)}、{Rs，u(t)}、{Cs，u(t)}的决策，具体算法如算法1所示。在每个时隙，中央控制器执行以下操作：（1）辅助变量。负责确定最优辅助变量；（2）速率控制。旨在找到最优接纳速率；（3）资源分配。该算法根据瞬时信道和干扰条件优化子信道分配和功率分配；（4）队列更新。执行上述决策后更新虚拟队列。

算法1基于QoE感知的公平资源分配算法

（1）辅助变量：求解子优化问题式(16)得到最优辅助变量{γs,u(t)}；

（2）速率控制：求解子优化问题式(17)以获得最优{Rs,u(t)}；

（3）资源分配：根据算法2找到最优子信道分配w(t)和功率分配P(t);

（4）队列更新：根据式(12)更新虚拟队列Z(t)，根据式(4)更新实际队列Q(t)。

3.1 辅助变量

在每个时隙，中央控制器可以观察Z(t)并通过求解以下子问题找到最优{γs，u(t)}。

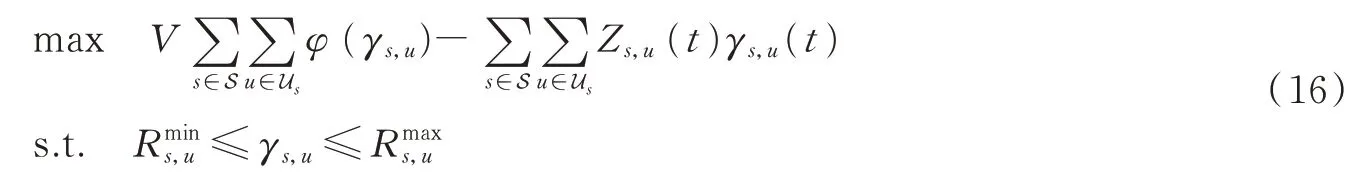
3.2 速率控制

该子优化问题的目的是寻找每个用户在每个时隙的最优接纳速率。速率控制优化问题可表示为

可以证明子问题式（17）是一个简单的线性规划问题，相应的最优解可表示为

3.3 资源分配

对于每个时隙t，可通过求解以下子问题来确定每个用户的最佳传输速率。

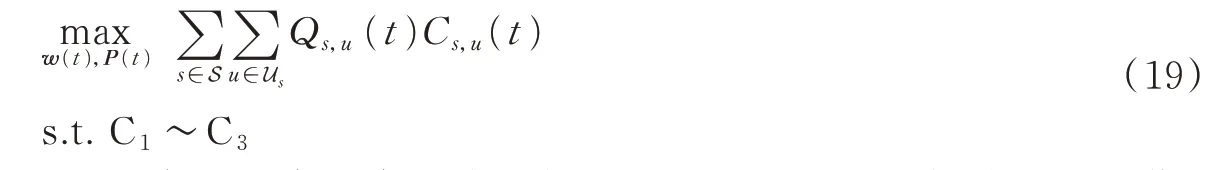
由于式（2）中传输速率函数的非凸性，求解混合组合非线性优化问题是一项具有挑战性的工作。为了有效地解决联合子信道分配和功率分配问题，本文提出了一种交替优化方法，将资源分配问题式（19）分为固定子信道分配的功率分配和固定功率分配的子信道分配两个子问题。通过交替迭代求解这两个子问题，可以得到资源分配问题的局部最优解。算法2描述了详细的算法流程。

算法2资源分配算法

初始化：设置初始值w[1](t)，令l=1。

重复

令k=1；

重复

k=k+1

对于固定P[l](t)=P^(t)，根据式（24）获得最优子信道分配w[l](t)；

l=l+1；

直到P(t)，w(t)收敛

3.3.1 固定子信道分配的功率分配

对于给定的子信道分配w(t)，功率分配问题是一个非凸非线性规划问题。本文将原问题转化为两个凸函数的一系列差分问题（Difference-of-two-concave-functions，D.C），并用逐次凸逼近法求得最优解。定义，其中

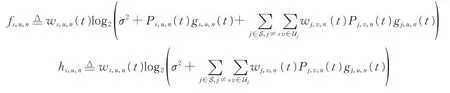
需要指出的是，fs，u，n和hs，u，n是凸函数。因此，子优化问题式（19）在给定的w(t)下的优化问题可以表示为关于P(t)的D.C函数，可以写成

根据文献［22］，优化问题式（20）可以用D.C规划方法来解决，它可以通过迭代求解一系列经典凸优化问题来快速收敛到局部最优点，这些问题定义如下

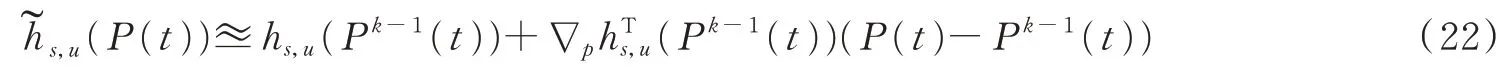
根据文献［21］，上述每一次迭代中的凸优化问题都可以用经典的凸优化方法如内点法或可用的软件包如CVX在多项式时间内有效地求解。

3.3.2 固定功率分配的子信道分配

可以很容易得出，在最优子信道分配方案中，每个子信道分配给传输速率最大的用户，即

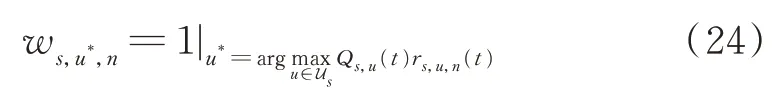
4 仿真设置及结果分析

4.1 仿真设置

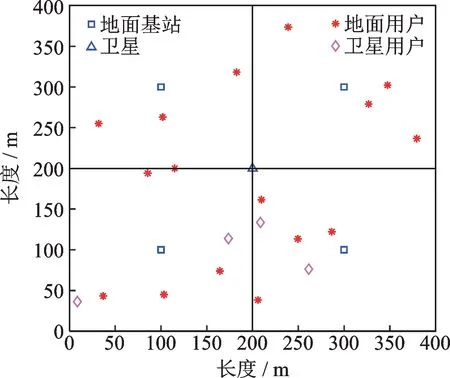
图2 仿真部署场景Fig.2 Simulation scenario

考虑在模拟场景中部署4个200 m*200 m网格方形的同层干扰地面无线网络。在每个方格中心部署一个地面基站并随机部署4个地面用户，如图2所示。同时，随机在网格中部署4个卫星用户。用户可以使用4种视频流服务，每种服务都可以通过参数[β1，β4]来区分。每个用户的参数[β1，β4]可以从[β1，β4]=［128 Kb/s，384 Kb/s］，［64 Kb/s，521 Kb/s］，［128 Kb/s，700 Kb/s］，或［8 Kb/s，3 400 Kb/s］中按照概率［0.113，0.378，0.459，0.05］随机选择。地面基站和卫星复用的载频为2 GHz，可用子信道数设置为6，每个子信道的带宽为180 kHz。每个地面基站的最大发射功率为17 dBm，AWGN功率谱密度为-174 dBm/Hz。路径损耗模型为128.1+37.6lgd，其中d（km）为用户与地面基站之间的距离。卫星最大发射功率为79 dBW，与用户距离36 000 km，路径损耗公式为92.45+20lgF+20lgd，其中F（GHz）表示载频，d（km）为卫星与用户之间的距离。仿真模拟时间为T=3 000个连续时隙，李雅普诺夫参数V=107。

所提策略主要从平均长时QoE、最小长时QoE和公平性3个方面对该方案的性能进行评估。公平性性能采用Jain公平性公式对长时QoE公平性指数进行评价，其表达式为

4.2 结果分析

通过模拟3 000个时隙，监测每个时隙的QoE的时间平均值作为长时QoE性能，得到了仿真结果。这里评估了在不同公平性参数α=[0，1，5，∞]下的平均长时QoE、最小长时QoE和公平性性能。图3～5分别显示了不同公平性参数下的平均长时QoE、最小长时QoE和公平性性能。

首先，从图3～5可以很容易地发现，QoE评估性能随着模拟时间的增加而稳定。这是因为网络中的所有队列Qs，u(t)都是平均速率稳定的，这将保证网络的稳定性。

图3展示了不同公平性参数下的平均长时QoE性能。结果表明，随着公平性参数的增加，平均长时QoE性能下降。例如，平均长时QoE性能为α=0时得到最高值，而平均时间平均QoE性能为α=∞时得到最低值。根据前面的描述，α=0、α=1和α=∞分别表示长时QoE总和最大化、比例公平和最大-最小公平。公平性参数α取值越大，用户的平均长时QoE性能之间的公平度越高。因此，在较低的公平性参数下，网络更倾向于优化网络的整体长时QoE性能。而在较高的公平性参数下，网络更倾向于均衡优化每个用户的网络性能。因此，较低的公平性参数设置可以获得更好的网络整体时间平均QoE性能。

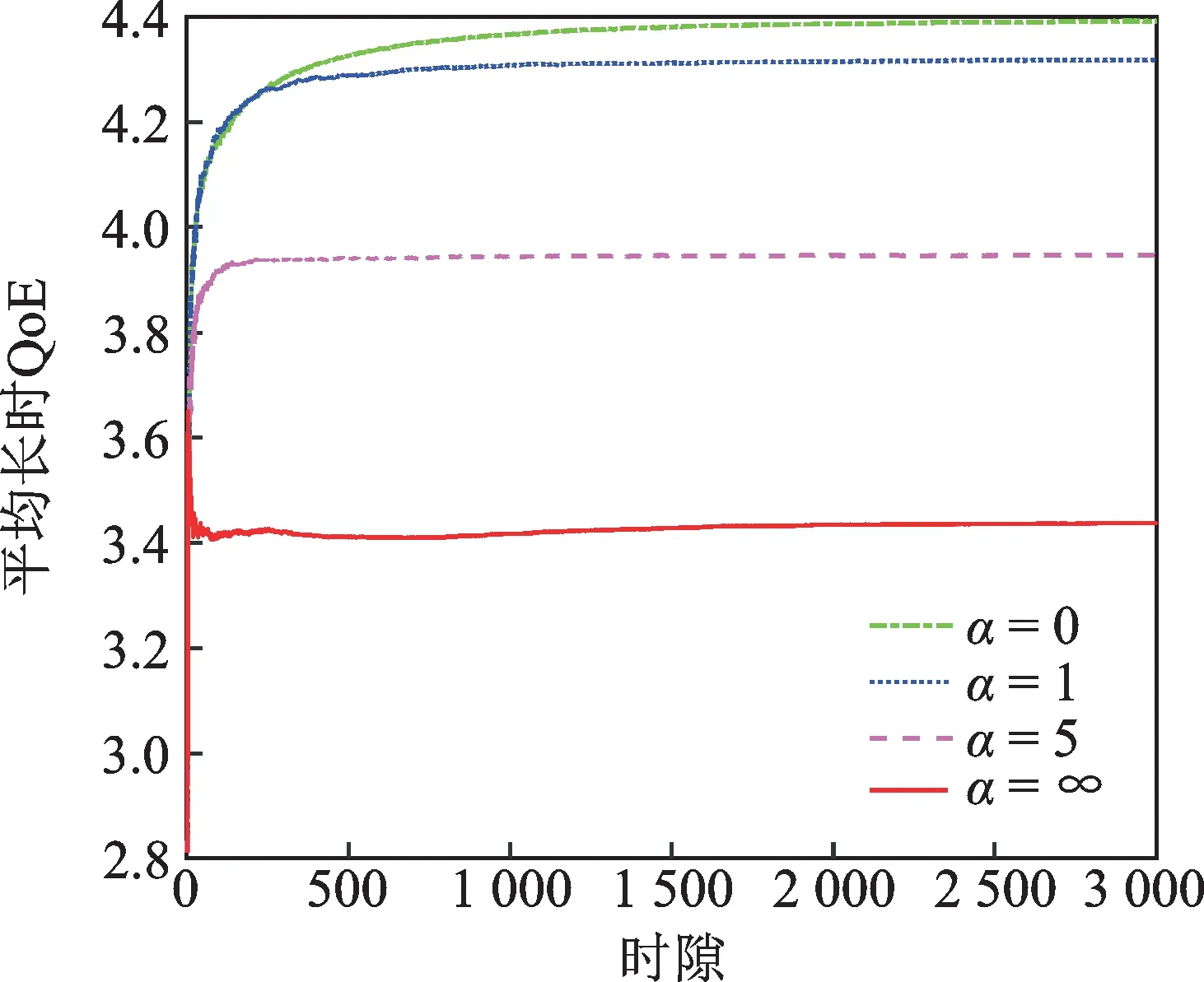
图3 不同公平性参数下的平均长时QoE性能Fig.3 Time-averaged QoE performance under different fairness parameters

图4显示了不同公平性参数下的最小长时QoE性能。可以观察到，最小长时QoE随着公平性参数的增加而增大。例如，α=∞最小长时QoE性能得到最大值3.5，而当α=0时仅能达到约2.5。这是因为，在较高的公平性参数设置下，网络会给予长时QoE较低的用户更多的调度优先级，以获得更多的无线资源，弥补性能上的不足。因此，较高的公平性参数设置可以保证用户具有更好的最小长时QoE性能。

图4 不同公平性参数下的最小长时QoE性能Fig.4 The minimum time-averaged QoE performance under different fairness parameters

图5显示了不同公平性参数下的公平性性能。可以很容易地看出，随着公平性参数的增加，长时QoE的公平性性能得到改善。例如，α=∞的公平性能可以达到接近100%，而α=0的公平性能只能达到95%。

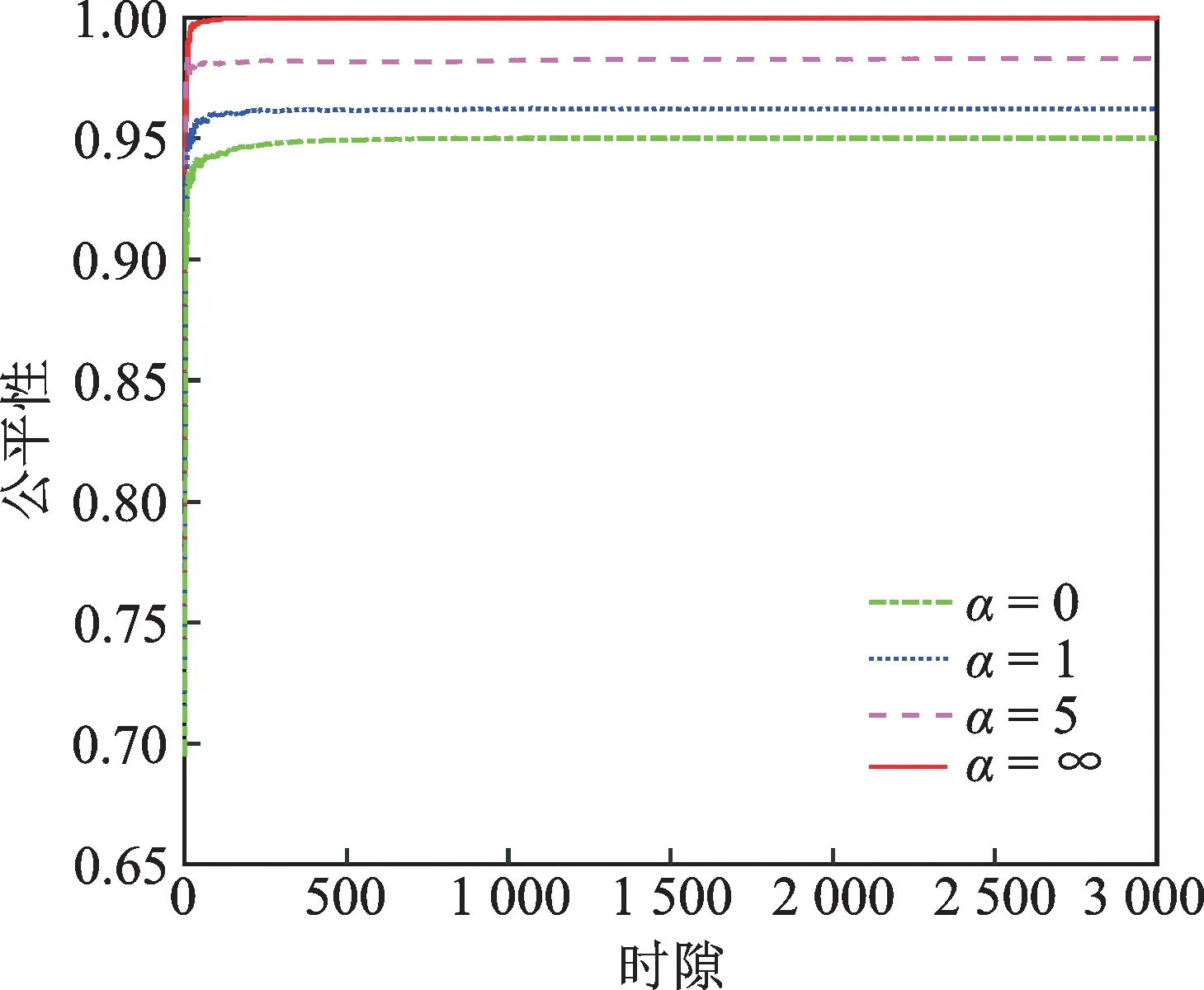
图5 不同公平性参数下的长时QoE公平性性能Fig.5 The Jain’s fairness performance under different fairness parameters

总之，较高的公平性参数设置可以减少用户间的性能差异，提高最小长时QoE性能。公平性参数越低，用户间的性能差异越大，但平均长时QoE性能越好。因此，在优化网络的时均QoE性能时，应综合考虑各种因素，设置合理的公平性参数，以有效平衡网络整体和用户个体的性能要求。

5 结束语

本文考虑了信道时变性，用户体验质量多样性和公平性等3个因素，提出了一个具有一般性的基于QoE感知的星地一体化网络公平资源分配策略。基于时间平均用户服务体验质量建模，将优化问题描述为用户长时QoE公平效用的最大化问题，并利用李雅普诺夫优化理论将原始问题进一步分解为3个瞬时优化子问题。每个子问题可以在每个时隙独立求解。此外，本文还提出了一种交替优化方法来求解第三个非凸混合组合优化的资源分配子问题。仿真结果评估了不同公平性参数下用户的长时QoE与公平性之间的折衷。因此，在现实中，应综合考虑各种因素，设置合理的公平性参数，以有效平衡整体网络和个人用户服务体验的性能要求。