三脉冲冷原子陀螺仪中基于内态演化的拉曼光光强补偿算法

黄 晨，乐旭广，程 俊，姚辉彬，毛海岑

(华中光电技术研究所， 武汉光电国家研究中心，武汉 430223)

0 引言

原子陀螺仪[1-3]作为一种基于量子力学的陀螺仪系统，因高精度、低漂移等特性而受到了广泛关注[4-7]，其理论精度相比目前应用的光纤陀螺高出11个量级。并且由于其不存在机械磨损，在长航时测量时不需要定期进行校准[7-10]，因此，应用原子陀螺仪构成的惯性测量单元(Inertial Measurement Unit，IMU)十分适用于潜艇等需要长时间惯性导航的装备。原子陀螺仪主要分为无自旋交换弛豫(Spin-Exchange Relaxation Free，SERF)陀螺仪[11]、核磁共振陀螺仪[12-15]，以及冷原子干涉式陀螺仪。目前，我们研制的冷原子陀螺仪是基于对抛型三脉冲Mach-Zenhder干涉仪，使用三束频率不断改变的拉曼光与原子相互作用，最终通过测量原子的内态分布，并对两个原子团干涉所得到的相位进行差分，从而分离出相应的转动信息及加速度信息。

原子陀螺仪敏感到外界转动信息的本质在于拉曼光与原子相互作用的频率失谐量随着外界载体的角运动及线运动(速度、加速度)的改变而实时改变，通过三束拉曼脉冲(π/2,π,π/2)将该频率失谐量转化为干涉仪相位，并且通过相应的解算可以得到外界载体的运动信息。在一个理想的三脉冲系统中，必须保证三束拉曼脉冲为π/2,π,π/2构型，此时才能维持测量值与输出值稳定的函数关系。在外界复杂环境下，不能保证拉曼光激光器的功率稳定性与实验室环境下类似。而拉曼光功率的变化直接影响原子与拉曼光的作用效率，即直接改变相互作用拉比频率。随着拉比频率的改变，三束拉曼脉冲不再是理想构型，而会使脉冲宽度发生改变。因此，此时干涉仪的输出值会随拉曼光光强的改变而产生相应的变化。若此时不对该结果做出相应的补偿，而依旧用原函数关系对陀螺仪输出值进行解算，就会产生误差。因此，为了保证在实际应用中陀螺仪的精度，必须建立关于拉曼光光强的补偿算法。在陀螺仪中，由于转动带来的频率失谐量的变化与拉比频率量级类似，并且无法在单拉曼光构型的干涉仪中通过类似重力仪的啁啾补偿同时对两团原子的频率失谐量进行补偿(两团原子的频率失谐量大小相等，符号相反)，因此只能通过数据后处理而非实时补偿的方式对该误差进行修正。

本文从拉曼光与原子相互作用的内态演化方程出发，对冷原子干涉过程进行建模，根据实际拉曼光强度的变化推导了原子陀螺仪在不同拉曼光强度下的相位输出值，并根据该关系式提出了一种通过监控拉曼光光强的变化对实际冷原子陀螺仪输出值进行后处理的补偿算法。

1 冷原子陀螺仪拉曼光光强补偿算法

基于内态演化矩阵，可以得到在含有拉曼脉冲时原子内态的演化如式(1)所示[10]

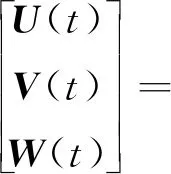
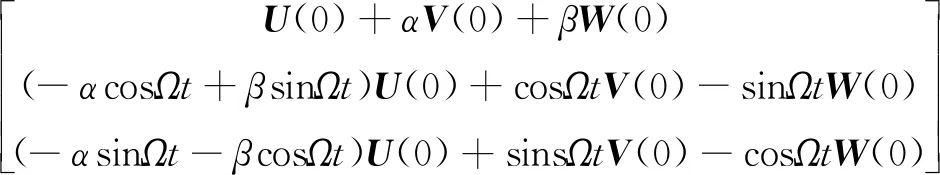
(1)

其中

(2)

代入可得

(3)

U(0)+cosΩtV(0)-sinΩtW(0)

cosΩtV(0)-sinΩtW(0)

(4)

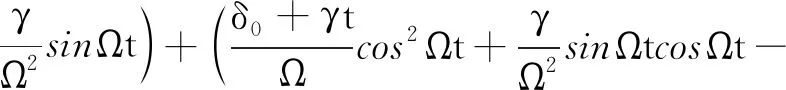
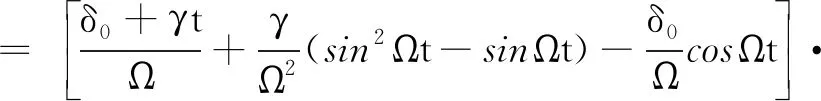
U(0)+sinΩtV(0)+cosΩtW(0)

(5)

在自由空间中演化的演化矩阵为

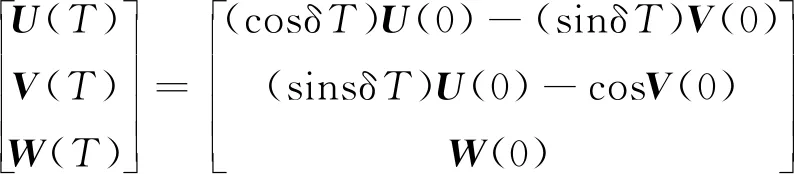
(6)

由于原子初态为

U(0)=V(0)=0,W(0)=1,δ0=0

则通过计算可得

W(3)=K1γ3+K2γ2+K3γ+K4

(7)

其中

K1=A1A2A11cosδbTsinδaT-

A1A5A11sinδbTcosδaT

(8)

K2=(A1A11-A2A3A11+A1A5A12)·

cosδbTcosδaT+(A1A3A12-A2A5A11-

A1A6A11)sinδbTsinδaT+A4A11cosδbT+

A1A8A13cosδaT

(9)

K3=(A2A11+A2A5A12+A1A6A12)cosδbT·

sinδaT+(A1A12-A2A3A12+A2A6A11)·

sinδbTcosδaT+(A7A11+A4A12+A1A9A13+

A2A8A13)sinδbT

(10)

K4=A2A12sinδbTsinδaT-A2A6cosδbTcosδaT-
A7A12cosδbT-A2A9A13cosδaT+A10A13

(11)

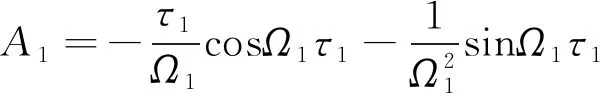
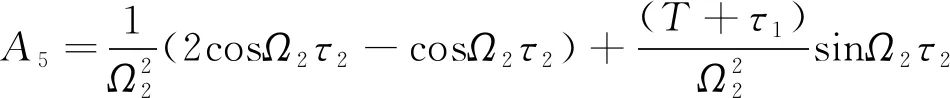
A9=sinΩ2τ2
A10=cosΩ2τ2cosΩ1τ1

A12=sinΩ3τ3
A13=cosΩ3τ3

(12)

2 补偿方法

通过式(7)～式(12)，可以建立对拉曼光光强的补偿方法如下：

1)在系统初始化时对拉比频率进行初始化，通过测量三束拉曼光的持续时间τ1,2,3分别得到三束拉曼光拉比频率的初始值

(13)

2)通过高速PD监测初始拉曼光强度I0；

3)通过高速PD监测测量过程中拉曼光强度变化的相对值ξ(t)。

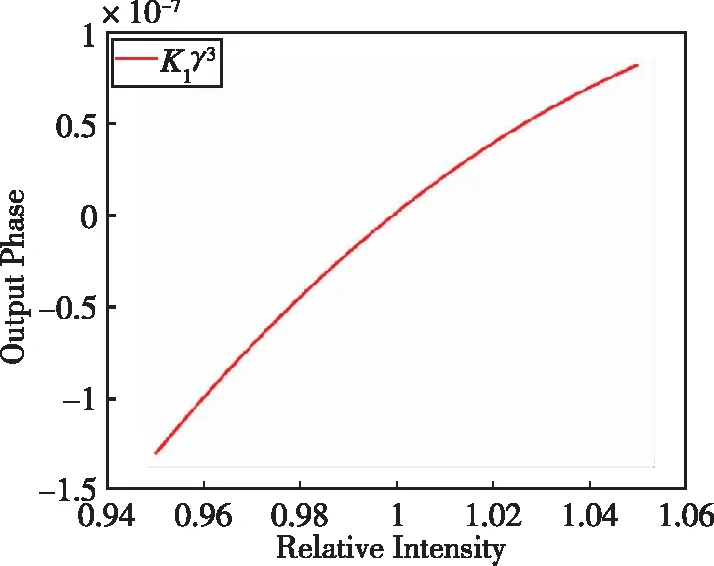
(a)系数k1γ3～1×107

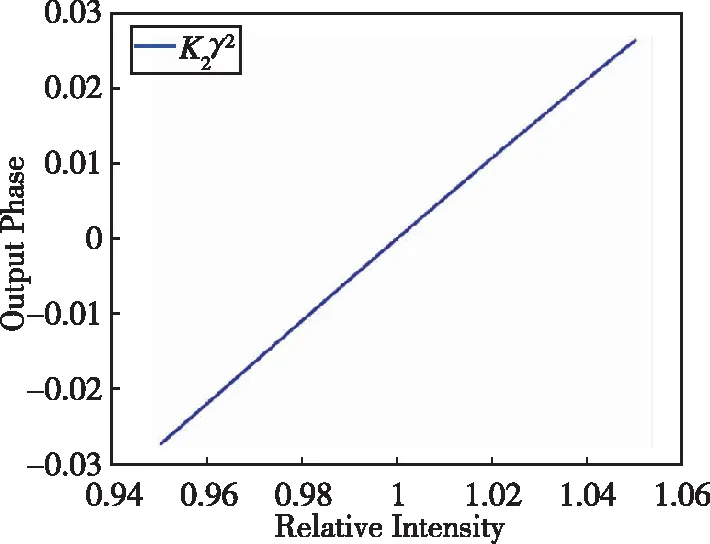
(b) 系数K2γ2～1×10-2

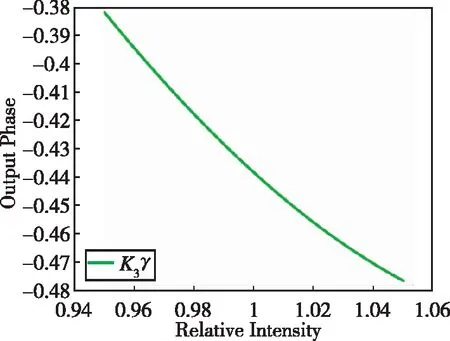
(c)系数K3γ～4×10-1

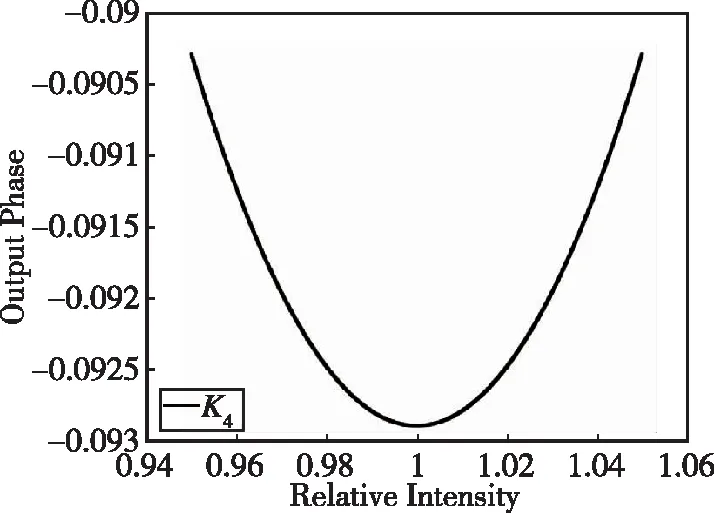
(d) 系数K4～1×10-2图1 第三束拉曼光后原子布居系数示意图(这里取转速Ω=1rad/s，T=3ms，keff=1.6×107)Fig.1 Paramters of the atomic population after the third Raman pulse (for Ω=1rad/s，T=3ms，keff=1.6×107)

则可以得到实际的拉比频率为Ω1,2,3ξ(t)，以及系数A1～13每一项的值。将其代入式(7)～式(11)，就可以通过计算机求解γ的值。对于可能存在多个根的情况，可以通过未补偿时所求得的转速进行筛选，筛选出最接近的值即可。则最终补偿后的实际转速为

(14)

若实际情况中，拉曼光光强稳定性较好，而拉曼光持续时间并不稳定(例如存在声光调制器响应较慢的情况)，则可以用如下方法对拉曼光持续时间进行补偿：

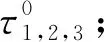
2)通过高速PD监测初始拉曼光实际持续时间τ1,2,3；

至此，将时序变化等效地转化为拉曼光强度变化。因此，可以通过相似的方式得到实际转速值。

3 实验验证

为了验证上述拉曼光光强补偿算法的有效性，进行了拉曼光强度调制实验。在实验中，通过对声光调制器的输出功率进行改变，使拉曼光功率随时间改变，由于声光调制器为非线性器件，无法直接记录其功率因子等价为光强信息，因此在敏感单元内部架设了高速PD对拉曼光强度进行实时测量，如图2所示。

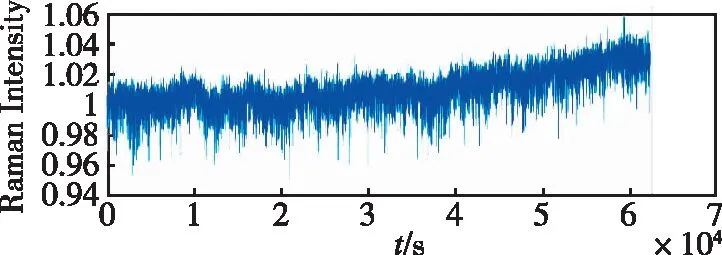
图2 拉曼光相对强度随时间变化图Fig.2 The diagram of relative intensity of Raman pulse over time

相应地，计算此时陀螺输出值的阿伦方差可以看出，最低点约为6×10-4，并且出现了明显的上翘现象，如图3所示。

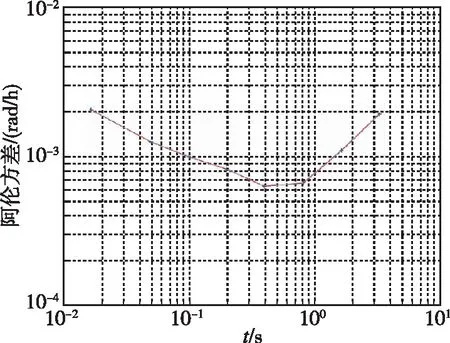
图3 拉曼光强度调制实验补偿前陀螺输出值阿伦方差Fig.3 The Allan deviation of the output of the atomic gyroscope before compensation in Raman intensity modulation experiment

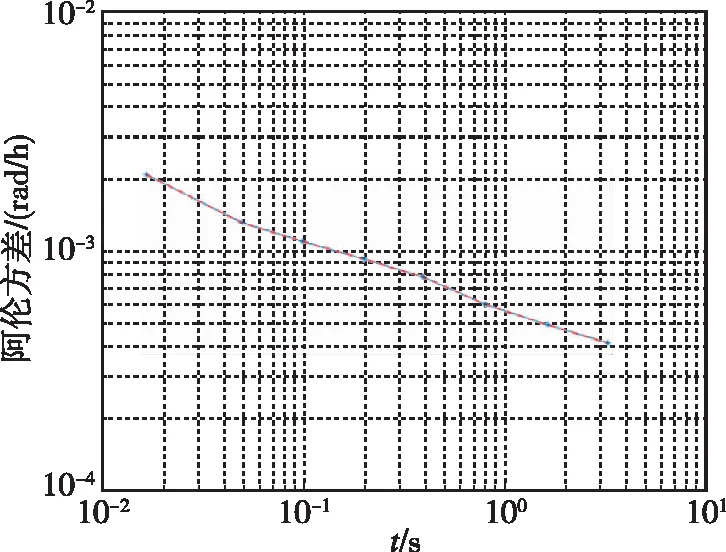
图4 拉曼光强度调制实验补偿后陀螺输出值阿伦方差Fig.4 The Allan deviation of the output of the atomic gyroscope after compensation in Raman intensity modulation experiment

随后，可以看到，在利用测量得到拉曼光相对强度并通过上述补偿方法进行补偿后，陀螺输出值得到了显著改善，如图4所示。从图4中可以发现，此时阿伦方差最低点下降至4×10-4，并且还在持续下降中，并没有出现上翘现象。相比未补偿情形，将系统长期稳定性提升了至少33%。这表明该补偿算法对拉曼光强度漂移带来的误差有很好的抑制作用。

4 结论

本文主要分析和讨论了冷原子陀螺仪在拉曼光光强变化条件下的响应，得到如下结论:

1)通过推导得到在光强变化时原子陀螺测量值的理论表达式，并给出了相应的补偿算法；

2)提出了通过高速PD对拉曼脉冲的强度以及宽度进行实时监测并记录数据，根据上述补偿算法对实际输出值进行补偿；

3)通过实际调制实验发现，该补偿算法对系统长期稳定性的提升幅度达到33%，并显著改善了系统误差的发散现象。