基于数值微分计算的SERF原子自旋惯性测量动态仿真

裴宏宇，杨功流，全 伟，段利红，黄 炯

(1.北京航空航天大学仪器光电学院，北京 100191；2.北京航空航天大学前沿科学技术创新研究院，北京 100191；3.北京量子信息科学研究院，北京 100193)

0 引言

作为惯性导航系统的核心部件，新型陀螺仪成为现今仪器仪表的研究热点[1]。基于多种物理原理，产生了许多新型陀螺仪，如基于光子或原子Sagnac效应的光纤陀螺与冷原子干涉陀螺[2]、基于原子自旋的无自旋交换弛豫(Spin Exchange Relaxa-tion Free，SERF) 陀螺仪[3]和核磁共振陀螺仪[4]。其中SERF陀螺仪体积小、对加速度不敏感且在理论上具有更高的惯性测量灵敏度，成为了下一代高精度陀螺仪的发展方向之一。

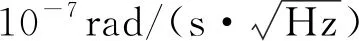
本文采用Bloch微分方程组对SERF原子陀螺的输入输出进行建模，搭建了Simulink仿真模型，对Bloch方程进行数值求解。测试了不同角速度和磁场输入下的输出动态响应曲线，并与理论计算进行对比。试验结果表明，Bloch方程的数值求解结果与理论求解结果一致，且数值求解可用于复杂输入下的输出动态求解，较理论解析求解具有更强的适用性。

1 SERF原子自旋陀螺的动力学模型

SERF原子自旋陀螺仪的原理图如图1所示，样机主要包括保证SERF态零磁场的磁屏蔽系统与磁场补偿线圈；保证SERF态高原子密度的加热系统；包含多种元素如钾、铷、氖、氮气的惯性敏感元件；发射处于电子跃迁频率圆偏振激光的抽运系统；以及线偏振光光旋角检测系统[10]。

图1 SERF原子陀螺结构[19]Fig.1 Structure of SERF gyroscope [19]

SERF原子自旋陀螺仪工作在多物理场耦合的环境中，无法通过解析求解的方法进行计算。故通过对原子陀螺的动力学特性分析，建立了Bloch方程组描述电子极化率与核子极化率随物理场的变化，并搭建Simulink仿真模型分析各物理场对输出的影响。SERF陀螺的基本测量原理如下。

当物体绕惯性空间的某一轴线做角速度为Ω的转动时，动量矩矢量H在载体空间与惯性空间的变化率有如下关系[11]

(1)

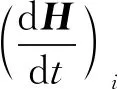
考虑如图2所示的二能级系统，当一束与原子跃迁频率相同的圆偏振光σ+沿z轴入射时，处于基态能级4S1/2,mJ=-1/2的电子能够吸收一个光子并跃迁到激发态4P1/2,mJ=+1/2；但处于基态能级4S1/2,mJ=+1/2的电子由于角动量不能够继续增加，不能吸收σ+光子跃迁到高能态。跃迁到高能态的电子与淬灭气体碰撞，等概率地落入4S1/2,mJ=-1/2和4S1/2,mJ=+1/2两低能级且不释放光子。在光泵浦的循环中，4S1/2,mJ=+1/2能级的光子逐渐多于4S1/2,mJ=-1/2能级的光子，此过程称为激光泵浦原子极化过程。

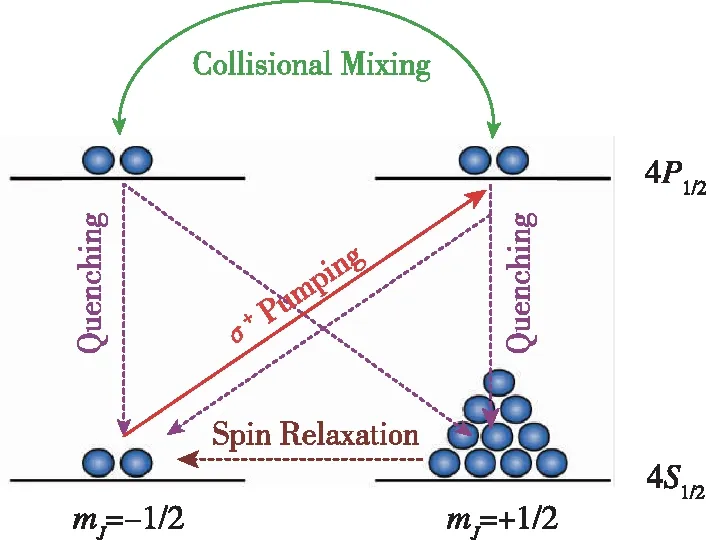
图2 碱金属原子中电子的光抽运[12]Fig.2 Optical pumping of electrons in alkali metal atoms[12]

此外，4S1/2,mJ=+1/2能级的原子可以通过弛豫效应返回4S1/2,mJ=-1/2能级，且在低磁场高碱金属密度的无自旋交换弛豫条件下，碱金属电子自旋的横向弛豫率与纵向弛豫率趋于一致，即[13]

(2)

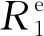
SERF原子自旋陀螺仪的碱金属电子与惰性气体核子通过各自的磁矩互相耦合，碱金属电子可以感受到惰性气体核子产生的磁场λMnPn，惰性气体核子会感受到电子自旋产生的磁场λMePe。普遍采用Bloch方程组描述SERF原子自旋陀螺的动力学特性[16]

(3)

(4)

式(3)右边第一项表示电子极化率在外加磁场、核自旋产生磁场以及光频移赝磁场的共同作用下进行拉莫尔进动(Larmor Precession)；第二项表示载体空间与惯性空间之间的转换关系；第三项分别表示抽运光与检测光对碱金属的抽运效应、碱金属电子与惰性气体核子之间的自旋交换效应与碱金属电子的弛豫效应，其中Rtot=Rp+Rrel。式(4)右边第一项表示核子极化率在外加磁场和电子自旋产生磁场的共同作用下进行拉莫尔进动；第二项表示载体空间与惯性空间之间的转换关系；第三项表示碱金属电子通过自旋交换碰撞对惰性气体核子进行超极化；最后一项表示核子的弛豫率。从Bloch方程组中可以看出，碱金属电子与惰性气体核子极化率通过彼此产生的磁场、核子与电子自旋交换碰撞相互耦合，彼此影响，Bloch方程组中各项符号的含义如表1所示。

表1 Bloch方程中符号的意义

SERF原子自旋陀螺仪的动力学方程属于非线性微分方程组，较为复杂，无法求得解析解。且在输入复杂多变的情况下，无法分析电子极化率和核子极化率的变化，也不易分析陀螺的瞬态响应。为解决此问题，基于Bloch方程组建立了原子自旋陀螺动力学模型，并采用Simulink进行数值求解和仿真。为验证数值解的准确性，与理论推导所得结果进行对照。对式 (3)和式(4)描述的动力学微分方程组构建仿真系统如图3所示。

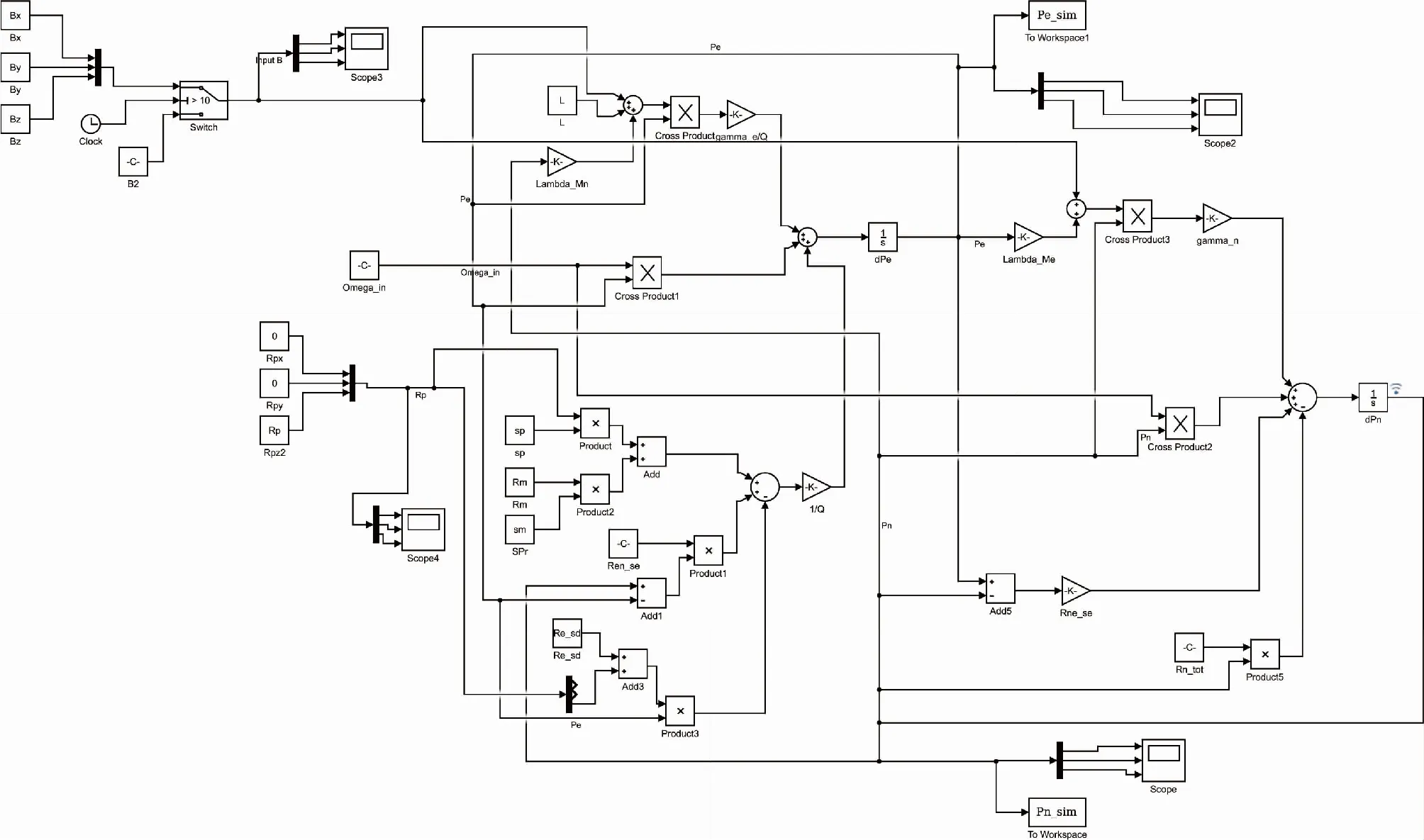
图3 SERF原子陀螺的Simulink仿真模型Fig.3 Simulink simulation model of SERF atomic gyroscope

2 SERF原子陀螺的数值仿真

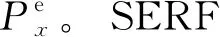
(5)

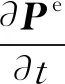
(6)

(7)

进一步地，碱金属电子与惰性气体核子的极化过程可以描述为[18]

(8)

(9)

当输入角速度或磁场时，可近似求得

(10)

(11)

(12)

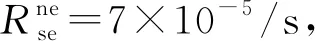
光抽运电子极化与核子超极化的过程如图4所示。由于电子的弛豫时间很短，在抽运激光的作用下，碱金属电子的极化率在0.03s快速达到了稳态值0.5984；由于大的弛豫时间，核子的极化率在12h达到了稳态值0.01451。通过式(6)理论计算，电子的极化率为0.60，仿真与理论计算的相对误差为0.13%；根据式(7)计算，核子的极化率为0.0146，仿真与理论计算的相对误差为0.048%，且仿真结果均略小于近似理论计算结果。式(6)中的理论计算忽略了碱金属电子与惰性气体核子的自旋交换碰撞作用对电子极化率的影响，自旋交换碰撞会将电子的角动量传递到核子上，造成电子极化率的微弱降低。故可以认为仿真模型的结果可以准确描述光抽运原子极化与核子超极化过程，且较理论计算进行了修正。

(b)自旋交换核子超极化图4 SERF原子陀螺光抽运电子极化过程与核子超极化过程Fig.4 Polarization process of optically pumped electrons in SERF atomic gyroscope and nucleon hyperpolarization process

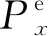
(a)电子极化率x分量

(b)核子极化率x分量图5 SERF原子陀螺在转动输入下的电子极化率响应与核子极化率响应Fig.5 Electron polarizability response and nucleon polarizability response of SERF atomic gyroscope under rotational input

为研究在磁场输入下SERF原子自旋陀螺的稳态解与该系统对干扰静磁场的补偿能力，设定补偿磁场Bz=256nT，当系统达到稳定的状态即5s后，在y轴方向施加一个By=10nT的阶跃磁场，系统响应如图6所示。

(a)电子极化率x分量

(b)电子极化率y分量

(c)核子极化率y分量图6 SERF原子陀螺在阶跃磁场输入下的响应Fig.6 Response of SERF atomic gyroscope under step magnetic field input

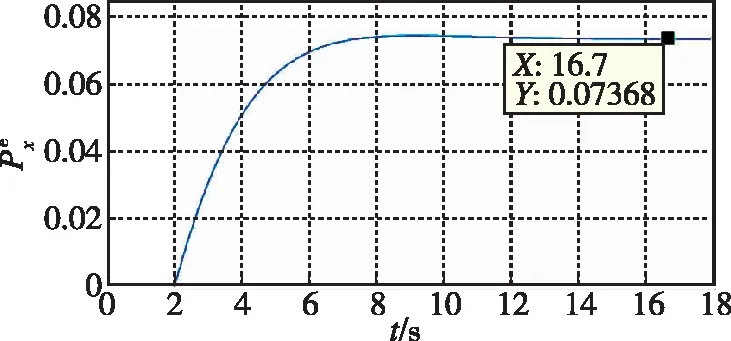
在实际使用中,追踪的角速度信号是时变的，采用匀速转动的方式虽能标定出陀螺仪随转动的稳态输出，但不能得到陀螺仪跟踪转动过程的动态性能。此外,由于输入信号复杂，不能通过理论计算得到解析输出结果。为研究陀螺仪对时变信号的追踪能力，对陀螺仪施加正弦角速度转动信号，测试陀螺仪对信号的追踪能力,并标定出本仿真参数下的陀螺仪带宽。仿真结果如图7所示。

为衡量SERF原子陀螺对输出的跟踪能力，采用角速度为sin(0.1t)rad/s、sin(0.3t)rad/s和sin(0.67t)rad/s的正弦信号进行激励。在sin(0.1t)rad/s的角速度输入下，陀螺仪的输出幅度为0.07337，接近阶跃角速度输入的输出响应值。随着激励信号角速度的增大，陀螺仪的输出信号逐渐减小。当输入角度的幅值不变，角速度达到sin(0.1t)rad/s时，输出降低至阶跃响应的70.7%即0.05367，故该仿真参数下陀螺仪的带宽为0.67rad/s。

(a)角速度输入sin(0.1t)rad/s

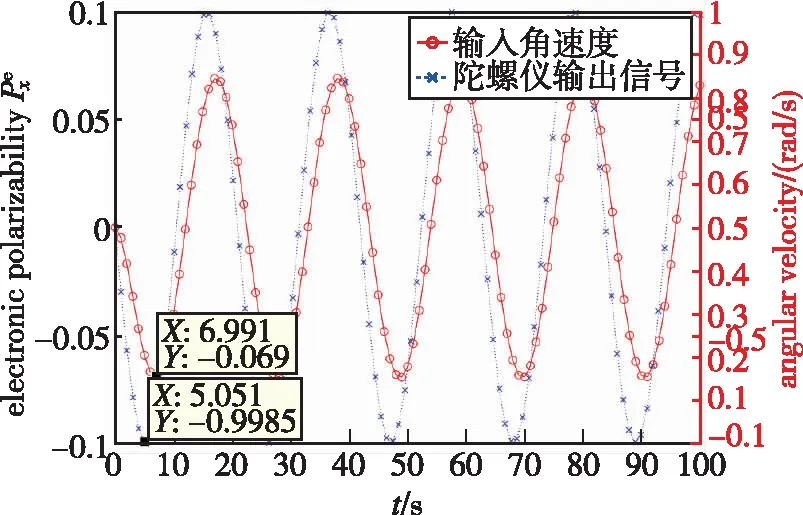
(b)输入角速度sin(0.3t)rad/s

(c)输入角速度sin(0.67t)rad/s图7 SERF原子陀螺在正弦转动信号输入下的响应Fig.7 Response of SERF atomic gyroscope under sinusoidal rotation signal input

衡量在实际应用中陀螺仪的输入输出情况。在陀螺仪的带宽范围内，测试了陀螺仪输出对输入角速度的跟踪情况，构造了复杂任意波输入，计算并对比了陀螺仪输出Ωy与输入之间的关系，仿真结果如图8所示。从仿真中可以得出结论，该陀螺仪在带宽内对角速度的输入有较高的跟踪精度。

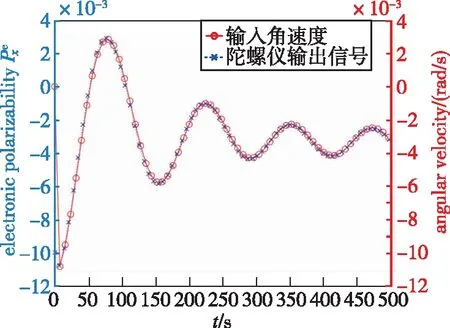
图8 任意波形输入下陀螺仪的输入输出关系Fig.8 Input output relationship of gyroscope under arbitrary waveform input

3 总结

本文从SERF原子自旋惯性装置的角速度测量原理出发,建立了Bloch方程描述其输入输出关系。为解决理论计算仅能得到Bloch稳态解,且输入磁场、角速度、光场时变时无法求解的局限性,建立了Simulink仿真模型,采用可变阶数值微分算法对Bloch方程组求解。对比了数值求解与解析计算的结果，验证了对Bloch方程进行数值计算的可行性与准确性,解决了复杂输入下无法通过理论解析计算求解SERF原子自旋惯性装置输出的问题。

影响SERF原子自旋惯性装置性能的因素有很多,如温度的不均匀性、磁场的不均匀性、抽运光检测光的偏振度等。本文验证了对SERF陀螺进行建模及数值求解的可行性与准确性,未来可以对更多影响因素进行研究,为SERF陀螺的设计与测试提供参考。