基于非导航随机信号的组合导航技术研究

王超奇，邵会兵，张 康，张 超，黄鹏宇

(1.北京控制与电子技术研究所，北京 100038；2. 清华大学，北京 100084；3.西安电子科技大学，西安 710071)

0 引言

全球导航卫星系统(Global Navigation Satellite System，GNSS)目前已经广泛部署并取得了巨大成功，最具代表性的系统包括美国的全球定位系统(Global Positioning System，GPS)、欧洲的伽利略(Galileo)系统、俄罗斯的GLONASS和中国的北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)。卫星导航定位系统的精度在一般情况下可以满足不同服务对象的定位要求。尽管定位技术已成熟，但卫星系统自身的一些特点仍会对定位产生不利影响，例如经过远距离传输，接收到的信号较弱，对接收机要求较高；信号在传输过程中会受到电离层的干扰，增加了定位的复杂度；卫星高速运动会产生多普勒效应，且其位置的不固定性也会导致增加和校对对应的定位参数，从而增大导航电文和设备开销。卫星定位最早始于军用，且常用于在开阔地带定位，而随着民用范围的扩大，在城市和室内定位的应用逐渐增多，但卫星定位服务并不理想，其在市区和室内等多径环境下实现高精度定位难度较大或代价很高[3-4]。

地面数字电视广播(Digital Television Terrestrial Multimedia Broadcasting，DTMB)信号则不存在上述这些不利因素，而且DTMB本身就广泛应用于人口聚居地，其信号相对于GNSS信号接收功率较高、频率较低、频带较宽，有些体制还采用正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术，使其相对有天然抗多径的优势。所以利用DTMB信号在上述环境中进行定位，在技术层面上具有可能性，从而可以成为卫星定位的有力辅助和补充手段。从应用层面来说，除完成其基本功能以外，DTMB信号作为一种无线电辐射资源，与其他无线资源如蜂窝网络、传感网络一样，亦可被考虑应用于各种军事和民事领域。目前已经有一些针对DTMB定位系统的研究。例如，美国的数字电视标准(Advanced Television Systems Committee，ATSC)体制中有利用场同步(Field SYNC)定位[3]或者在信号上叠加发射机标识序列TxID来区分发射塔进行定位[7]的方法；对于欧洲的数字视频广播(Digital Video Broadcasting，DVB)系列，亦有针对各自特点提出的定位方法[8-9]。而对于国标DTMB，则有学者提出了利用TDS-OFDM的特性，采用时频结合的测量伪距的算法[10]。

基于移动通信系统的定位系统，在当前3G、4G无线通信系统广泛部署的情况下可以有效地摆脱对全球卫星导航信号的依赖，同时通过合理的系统设计和算法构建同样可以获得较高的定位精度，以及较低的成本。随着互联网的快速发展以及智能手机的迅速普及，与手机相关的技术和服务也在不断的发展和完善。移动用户对信息的时效性和位置性的需求越来越强烈，手机定位服务逐渐成为移动通信领域的热点，逐渐被人们所关注。手机定位服务目前已广泛应用于紧急医疗、汽车救援、交通管理等领域，以满足移动执法、移动办公、物流配送、交通管理等业务的定位需求。

本文继承了导航技术的现有成果，并开展了基于DTMB、接收信号强度指示(Received Signal Strength Indicator，RSSI)移动终端等非导航随机信号的导航信息提取技术研究，以及不依赖卫星导航的组合导航技术研究，构建以惯导作为参考导航系统，并与数字电视信号、手机发射塔信号等随机信号导航装置构成组合导航系统，提高系统的抗干扰性能，实现复杂环境下的高精度导航定位。

1 组合导航系统基本原理

针对不同非导航随机信号测量信息的应用需求，结合不同应用的动态条件，设计了基于随机信号的组合导航技术，以适应位置、速度、距离、距离变化率、角度、时间等任意测量信息的组合。信息融合需对多源信息进行处理，首先要解决的关键问题是建立信息融合的总体框架，架构设计采用开放式结构，面向多种信号的共性需求，支持针对不同信号的通用化处理。下面以手机信号和数字电视信号等非导航信号为例，针对通用组合导航系统架构予以介绍，组合导航系统由惯性测量组件、卫导接收模件、手机信号模件、数字电视信号模件和信息处理模件组成。

1)惯性测量组合敏感载体的视速度增量和角度增量，经导航解算得到纯惯性导航下的载体位置PP和速度VP；

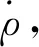
3)数字电视信号模件和手机信号模件作为卫星导航增强系统，完成载体和地面发射塔之间的距离测量。

信息处理模件综合惯性测量组件、卫导接收模件、手机信号模件、数字电视信号模件的测量信息，构造滤波系统的状态方程和观测方程，并进行线性化处理，然后通过Carlson滤波器估计惯性导航的位置误差ΔPP和速度误差ΔVP，进而修正惯导的位置和速度。该系统充分发挥多种导航资源和导航模式的优势，形成优势互补，一旦某种导航模式失效，系统仍能够提供精确的导航定位信息，并可与惯性导航系统形成组合导航系统，大幅提高了组合导航系统对高动态环境的适应能力，原理框图如图1所示。

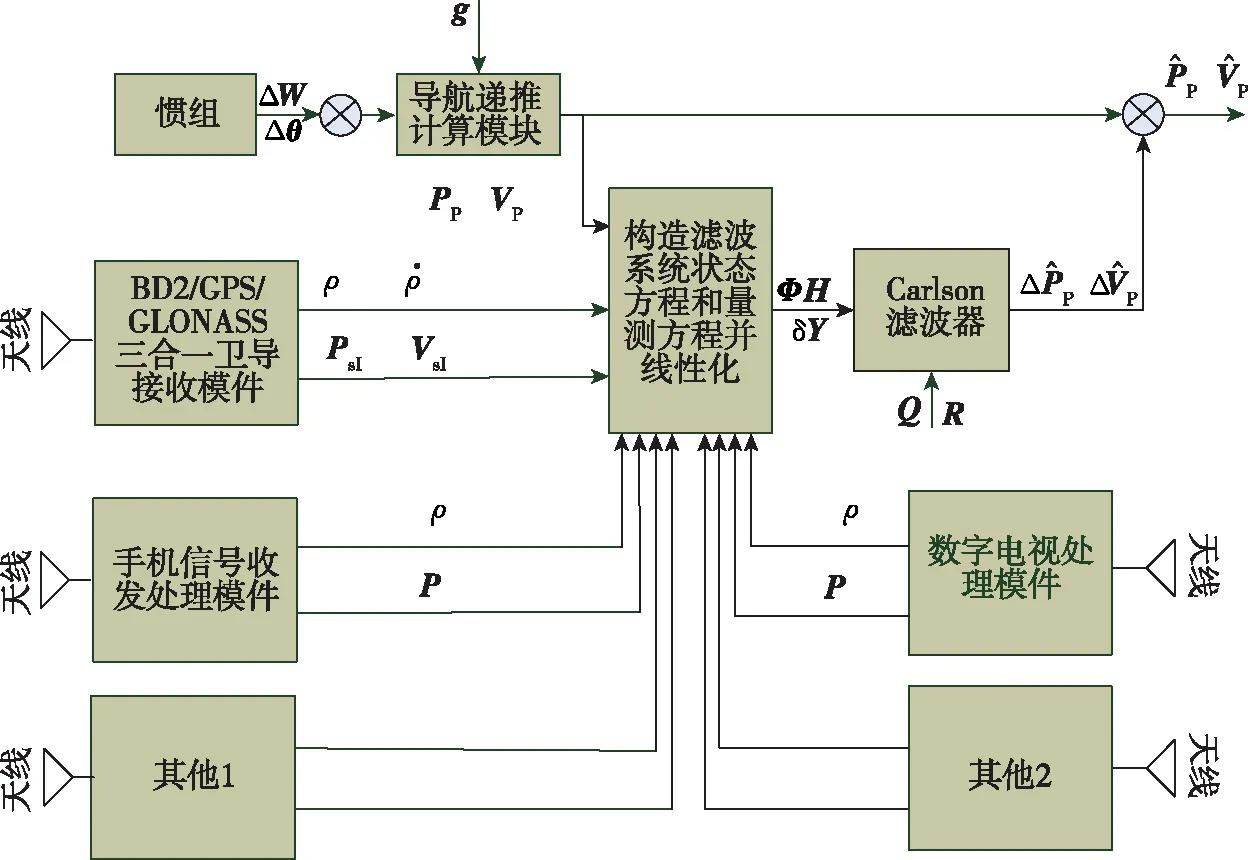
图1 组合导航系统原理框图Fig.1 Integrated navigation system block diagram

2 基于DTMB的测距技术研究

DTMB帧结构的基本单元是信号帧，信号帧由帧头和帧体两部分构成，基于DTMB的测距过程并不关心帧体包含的数据信息，只需要利用帧头已知的PN序列进行同步和提取传输时延，并利用不同的频率来区分发射塔。

设经过无线信道传输接收到的信号r(t)为

r(t)=s(t-τ)*h(t)+w(t)

(1)

式中，s(t)为发射端时域信号;*表示线性卷积;h(t)为信道冲击响应;ω(t)为加性高斯白噪声(Additive White Gaussian Noise, AWGN);τ为信号传输时延。

以采样周期Ts为单位进行归一化

(2)

式中，θ为归一化后的时延;θI为四舍五入后的整数时延;θF为舍入的分数时延，θF取值范围为[-0.5,0.5)。求出归一化的时延θ后，由于电磁波以光速传播，所以可以计算出发射塔与接收机之间的距离D=θTc。

由于PN序列具有良好的自相关特性，将接收到的信号r(n)和本地PN序列p(n)进行相关运算后, 找到相关函数最大的采样点即为整数时延θI[7]

(3)

式中，r*(n)表示接收信号r(n)的共轭转置。

DTMB的基带符号率为7.56Msps，以4倍过采样为例，此时采样率为30.24MHz，忽略分数时延造成的最大误差约为5m。因此，在较高的定位精度要求下，分数时延θF是不可忽略的。

在发射机和接收机中各有一个平方根升余弦(Square Root Raised Cosine, SRRC)滤波器，发射信号在经过两个平方根升余弦滤波之后相当于过了一个升余弦滤波器。升余弦滤波器的时域冲击响应如下

(4)

式中，T为时域采样信号的采样间隔，当以N倍采样率(Ts=T/N)对接收信号进行采样时，得到的时域信号为hd(n)=hc(nTs)，已知的整数倍时延的影响可以被补偿掉，因此只考虑分数倍时延带来的采样点偏移，最终采样后的时域冲击响应为

hd(n)=hc[(n-θF)Ts]

(5)

因此，在有明显的主径的信道下，高斯白噪声在相关运算中会相互抵消，所以最终接收信号中包含PN序列的部分与本地PN序列的相关函数R(k)如下

=p*(-k)*(p(k)*hd(k)+w(k))

(6)

式中，Rxx(k)是PN序列的自相关函数。PN序列具有良好的自相关特性，其自相关函数如下

(7)

式中，P是采样后PN序列的点数，以PN420及4倍过采样为例，P的取值为1680，因为P的值远远大于1，所以只需要考虑Rxx(k)峰值Rxx(0)的影响即可。所以最后相关函数R(k)可以表示为

R(k)=Rxx(0)hd(k)=Rxx(0)hc((k-θF)Ts)

(8)

假设第k个采样点的值为y(k)，y(k)在k=kmax处取得最大值，在采样点峰值左右两边再各取N个点(一共2N+1个点)，并利用最小二乘法计算分数倍时延θF。具体计算方法如下

(9)

设置好初始值M0和d0，通过迭代求解最优的M和d使得式(9)最小，此时d的取值即为分数倍时延θF。

3 基于RSSI移动终端的测距技术研究

RSSI移动终端根据测量得到的基站信号接收强度，通过无线信号传播模型对基站与被测终端之间的距离进行计算。基站发射的信号在经过一段距离的传播之后，根据自由空间传播模型，信号的强度将会逐渐衰减，即可利用强度衰减与距离之间的关系，根据初始强度及被测强度对距离进行估算，例如可以使用对数距离衰减模型,即

(10)

式中，p为当终端与基站之间的距离为d时信号的路径损耗；p0为距离为d0时的参考路径损耗，需要通过实际测量得出；n为路径损耗指数，表明路径损耗随距离增长的关系，其具体取值与环境有密切关系；ξ为正态随机变量，根据环境条件进行相应取值。

电波传播特性的研究是移动通信系统的关键技术之一，无线信道的传播特性与通信环境密切相关，具有很大的随机性。多年来，许多专家和学者对信道的传播特性进行了大量的分析研究，Okumura模型在全球移动通信(Global System for Mobile Communication, GSM)系统的路径损耗预测方面具有较高的精确度。

在Okumura公式中，经拟合获得的市区传播损耗基本公式为

L50(市区)=69.55+26.16lgf-13.82lghte-

α(hre)+(44.9-6.55lghte)lgd

(11)

式中，α(hre)为有效的移动天线高度增益校正因子，是覆盖区范围的函数。

由于Okumura模型是基于大量实验数据拟合得出的经验模型，为进一步提升精确度，可以将某地区具有代表性的充足实测数据代入公式后，通过线性回归等数学手段实现对模型的校正。对式(11)变化后用以下通用形式表示

L=k1+k2lgf+k3lghte+(k4-k5lghte)lgd

(12)

因此只需要确定k1、k3、k4、k5即可获得对传播模型的修正。此处可以在实际测试场景中选取若干测试点进行位置-场强测试，当测试数据的数量和代表性都足够时，采用最小二乘或线性回归等方法对测试数据进行拟合，就可获得式(12)中对应的系数，从而可精确计算出相对基站的距离。

4 组合导航系统算法研究

4.1 观测变量、状态变量的选取

观测变量主要包括卫导模件测量的伪距、伪距变化率以及手机信号模件/数字电视信号模件输出的距离信息等非卫星导航随机信号的测量信息。

状态变量的选取是滤波器设计的关键之一。本文涉及的状态变量可分两类，一类与惯性导航系统有关，状态变量选取惯导位置误差、速度误差、加表各项误差、陀螺漂移、初始对准误差等；另一类则与接收机有关，主要考虑接收机时钟的影响，如接收机钟差等。

4.2 构造状态方程

由于导航系统是连续的非线性系统，首先需要对其线性化。为了尽可能地减小由于线性化带来的误差，采用根据估计值计算的名义值附近展开进行线性化的方法，那么滤波时的状态量实际为估计值的残差δXr,在名义值附近展开，线性化后得到再入段组合导航滤波器的状态方程为

其中,Ar为状态转移矩阵。

4.3 构造量测方程

本文中，滤波系统直接采用各模件测量的距离和距离变化率等非导航随机信号的测量信息作为测量变量，以消除测量数据相关引起的组合导航精度下降问题。下面以卫导、数字电视和手机信号为例给出距离和距离变化率测量信息。

距离量测方程为

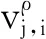
距离变化率量测方程为

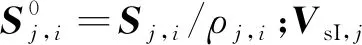
那么，可以得到线性化后的量测方程为

其中，δYr,j,i为距离、距离变化率测量量与名义值之差；Hr,j为量测矩阵。

5 仿真结果

基于非导航随机信号的组合导航技术研究成果，以低精度惯性导航为参考导航系统，融合数字电视信号、手机信号等非导航随机信号，开展了数学仿真、半实物仿真和跑车试验验证。数字电视信号测距精度如图2所示，手机信号测距精度如图3所示；数字电视信号发射塔和手机信号发射塔相对载体轨迹的分布如图4和图5所示；组合导航仿真结果如图6和图7所示。基于非导航随机信号的组合导航定位和测速精度分别在±10m、±0.1m/s以内。

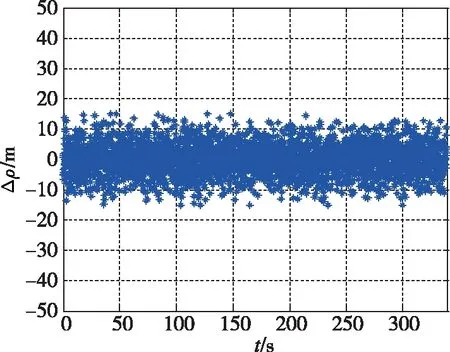
图2 数字电视信号测距精度Fig.2 Digital television signal ranging accuracy

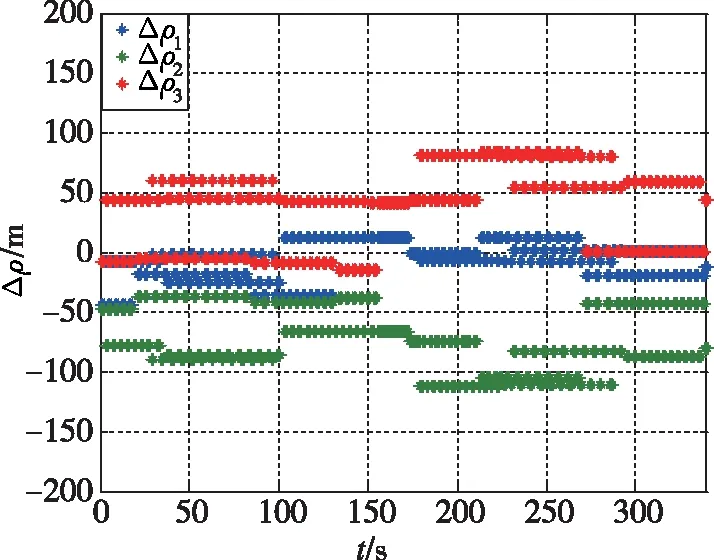
图3 手机信号测距精度Fig.3 Cell phone signal ranging accuracy

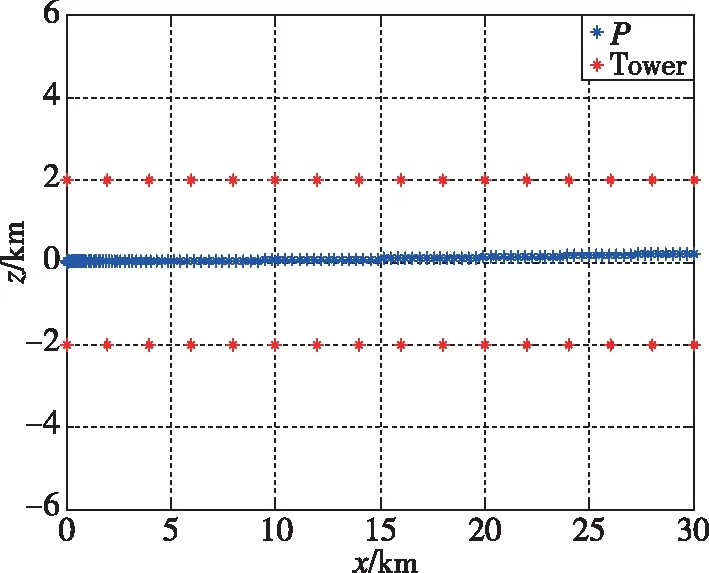
图5 手机信号发射塔相对载体轨迹的分布Fig.5 Distribution of mobile phone signal transmission tower relative to carrier trajectory

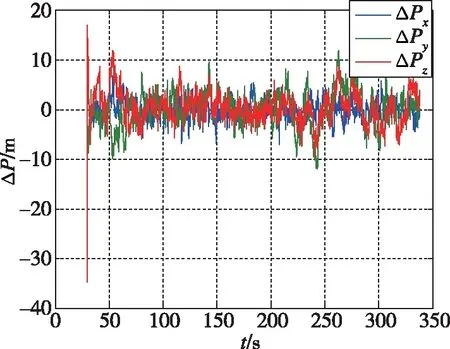
图6 定位精度Fig.6 Positioning accuracy

6 结论

通过理论研究和试验验证，可以得到以下结论：

1) 通过DTMB和RSSI移动终端等非导航随机信号可以提取高精度导航信息；

2)基于非导航随机信号的组合导航算法可以在较短时间内收敛，且精度可达到预期值，定位和测速精度分别优于±10m、±0.1m/s；

3)本文研究的基于非导航随机信号的导航信息提取技术和组合导航技术可以弥补卫星导航系统的不足，作为卫星导航的有效补充手段，能够提升复杂环境下的高精度导航能力，具有较强的实用价值。