基于带有事件触发机制的集员滤波的RSSI室内移动定位

王田田，杨 波

(山西大学数学科学学院，太原 030006)

0 引言

近年来，随着智能手机和平板电脑等移动智能终端的普及，人们对基于位置服务的需求日益增长。根据《室内外高精度定位导航白皮书》显示，导航与位置服务在新一代信息技术中具有举足轻重的地位。调查显示，人们80%以上的时间处于室内环境中(含地下、矿井、隧道、机场、火车站等)，因此室内位置服务具有广阔的应用前景[1]。众所周知，室外环境下，以空中卫星为基础的全球导航卫星系统(Global Navigation Satellite System，GNSS)被广泛应用且具有极高的精度。然而在室内环境下，由于卫星信号受到建筑物阻隔，导致GNSS信号快速衰减，使得GNSS无法满足室内定位需求。为了实现高精度的室内定位，基于超宽带(Ultra Wide Band，UWB)[2]、 无线射频识别[3]、WiFi[4]和Zigbee[5]等技术的各种室内定位系统得到了广泛研究。其中基于接收信号强度指数(Received Signal Strength Indicator,RSSI)的WiFi和Zigbee等技术具有低成本、低功耗、易部署等优势，使得基于RSSI的室内定位得到了广泛关注。

基于RSSI的距离测量方法的基本工作原理是利用RSSI值与距离之间存在的关系。根据移动终端测量接收到的信号强度和已知的无线测距模型，可以估算出收发方之间的距离。由于无线电信号在传输过程中容易受到环境的干扰，导致测量得到的RSSI值含有测量噪声，进而影响了定位精度。为了降低外界噪声对定位结果的影响， 常采用Kalman滤波[6]和粒子滤波等方法估计目标位置，然而这些方法要求知道噪声的统计特性。在许多实际应用中，噪声信号多是未知的，但是噪声的边界容易获得，因而可考虑采用集员滤波来处理未知但有界的噪声[7]，且集员滤波可以提供包含目标真实状态的集合，使得定位结果更可靠。

自文献[8]和文献[9]提出集员滤波后，集员滤波在理论与应用上都引起了很多学者的注意。文献[10]采用凸优化方法处理范数有界不确定系统的鲁棒集员滤波问题。文献[11]将集员滤波用于移动机器人定位。文献[12]解决了一类具有传感器饱和的离散时变系统的集员滤波问题。为了减轻通信负担，文献[13]采用事件触发通信协议处理离散非线性系统的分布式集员滤波问题。最近，文献[14]在基于RSSI的室内定位问题中采用了集员滤波算法，然而该文献仅研究了固定点定位问题，而没有考虑室内环境下移动节点的定位问题。 因此，本文采用集员滤波估计移动节点的位置，可以求出包含目标真实位置的区域，从而得到更可靠的位置估计，并且考虑了事件触发机制以降低节点的传输与计算负担。

结合集员滤波的特点，本文提出了一种改进的椭圆三边定位算法，克服了由于RSSI测距误差导致的三边定位算法无法获得可行解的问题，同时针对因目标移动而导致估计误差增大的问题，提出了一种锚节点自主选择与切换方法。 最后针对噪声统计特性未知的情况，考虑了带有事件触发机制的集员滤波方法来估计移动目标位置，以提高估计结果的可靠性，同时减少不必要的信息传输与计算，节约通信资源，降低能耗。

1 问题描述

本文研究了无线传感网络(Wireless Sensor Network, WSN)上基于RSSI的室内移动目标的定位问题。传感网络结构如图1所示，传感器i可接收来自待测节点的信息，也可接收两个邻居节点j和l的测量信息。定位系统的状态方程可用式(1)描述

xk+1=Akxk+Bkωk+uk

(1)

其中，xk+1∈R2表示系统状态，也就是移动目标位置；Ak和Bk是维度匹配的已知矩阵；uk是已知的控制输入；ωk∈R2是未知但有界的过程噪声，且满足

(2)

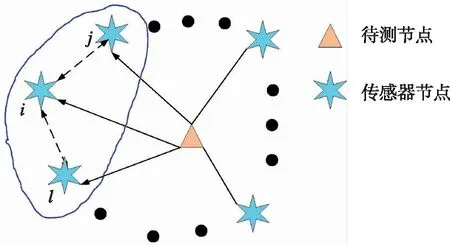
图1 传感网络结构示意图Fig.1 Structure of WSN

第i个传感器的测量方程为

(3)

其中，根据文献[15]有

(4)

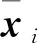
(5)

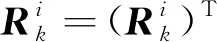
本文首先使用三边定位算法求解目标位置的初值，然后考虑通过切换传感器降低由于距离增长RSSI值衰减造成的估计误差增大的问题，最后采用集员滤波求解出包含目标真实状态的椭球。

2 三边定位求初值

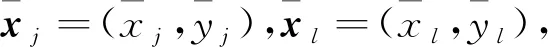
RSSI=A-10γlgd

(6)

式中，A和γ是与环境相关的系数，可通过线性回归法求得。由此可得

(7)

理想的三边定位算法是以锚点坐标为圆心、锚点到待测节点的距离为半径作圆，三个圆交于一点。然而，在实际应用中，由于环境影响，测量值RSSI可能存在误差，导致出现三个圆不交于一点甚至不相交的情况。针对这一问题，并结合集员滤波的特点，本文提出了一种改进的三边定位算法来计算集员滤波的初值。 在介绍算法前，先引入需要用到的来自文献[17]的两个引理。

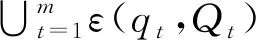
min log detA-1

s.t.λt>0,

t=1,…,m

(8)

然后，根据q=-A-1b,Q=(ATA)-1可以确定ε(q,Q)。

min log detB-1

s.t.λt>0,

(9)

然后，有Q=BTB。

本文提出的改进的三边定位算法步骤如下：

2)以锚点为圆心、锚点与待测节点之间的距离为半径作圆，三个圆可分别用式(10)表示

(10)

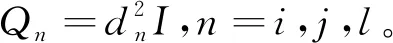
3)用引理1求出三个圆两两之间并集的最小外包椭圆，即

(11)

(12)

(13)

4)用引理2求出上一步中三个椭圆交集的体积最大内部椭球，即

(14)

(15)

本文所提的三边定位算法在三圆交于一点、交于一个区域或不相交的情况下都可以求出包含待测节点真实状态的椭圆。

3 锚节点切换与选择机制

随着目标移动，待测目标节点先接近传感器节点后逐渐远离，从而与当前锚节点之间的距离不断增大，其相应的RSSI值也随之先增大后衰减，如图2所示。且根据式(6)可知，随着距离的增大，RSSI 值对距离的改变也越来越不敏感，从而导致测量误差增大，因此本文提出了一种根据RSSI值范围选择锚节点的方法。以锚节点i为例，RSSI值与目标位置之间的关系为

(16)

从而有

(17)

(18)

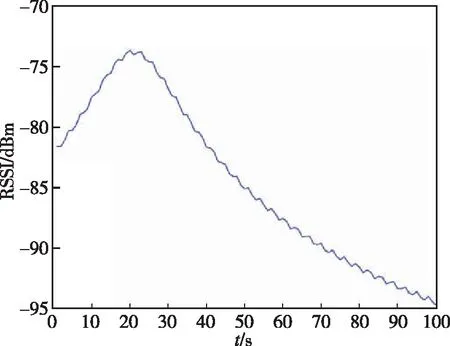
图2 RSSI值变化趋势Fig.2 Change of RSSI

根据式(6)，可得RSSI对距离d的导数为

(19)

令(RSSI)′<-δ，其中，δ>0为给定阈值，可得

(20)

从而有

(21)

选择RSSI值满足式(21)的锚节点作为下一个用于测量的锚节点，从而使RSSI保持在对距离变化足够敏感的范围内。

4 基于事件触发的集员滤波估计位置

4.1 节点i处的本地估计

(22)

滤波器为

(23)

(24)

其中

(25)

(26)

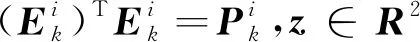
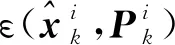
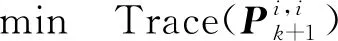
(27)

其中

1)基于微课的自主学习：翻转课堂顺利实施的技术支持就是微课，特别是在实践性较强的计算机公共类课程中，把微课作为辅助教学非常便利，学生可以不受时间、地点的限制，多次地通过观看微课进行知识的复习和强化。在具体实现时，根据不同的课程要求，教师构建基于微课的课程自主学习平台，平台主要包括以下功能：

(28)

Ξi,i=diag{1-τi,1-τi,2-τi,3,τi,1I,

(29)

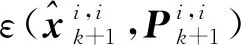
定理1的证明如下：

根据式(22)～式(24)有

(30)

令

(31)

从而有

(32)

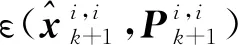
(33)

根据式(32)，式(33)可转化为

(34)

(35)

(36)

(37)

(38)

式(38)也等价于下面更紧凑的形式

(39)

通过使用文献[18]的Schur complement引理将式(39)转换为式(27)，证明完毕。

4.2 基于节点j的更新估计

(40)

其中，l为事先设定的触发阈值。

(41)

其中

(42)

(43)

(44)

定理2的证明如下：

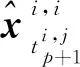
(45)

从而可得

(46)

设

(47)

因此，式(46)可转化为

φy,jξi,j=0

(48)

(49)

根据定理1有

(50)

因此可得

(51)

即

(52)

因此，式(49)可转化为

(53)

(54)

(55)

通过S-Procedure可得式(48)和式(53)～式(55)的等价形式

(56)

式(56)等价于

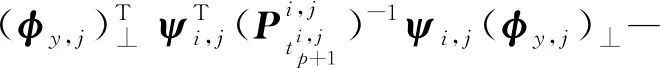
(57)

使用Schur complement引理可将式(57)转化为式(41)，证毕。

基于邻居节点l的信息交互估计与基于邻居节点j的信息交互过程类似，此处省略。

5 仿真验证

5.1 三边定位

考虑一个基于RSSI的室内定位系统，其中三个锚点坐标分别为[1,2],[2,1],[2.5,3]，待测节点坐标为[2,2]，三圆相交于一点、相交于一个区域，以及不相交情况下，采用本文所提三边定位算法求出的结果分别如图3所示。 图中蓝色细实线圆表示以锚点为圆心、锚点与待测点距离为半径所作的圆，黑色虚线椭球表示三个圆两两之间交集最小的外包椭球，紫红色粗实线圆表示最后结果。

图3(a)展示了三个圆不相交的情况下仍然可以获得可行解，所得椭球的中心点为[1.7256,1.8356]，用椭球中心点与待测节点之间的距离差表示估计误差，这种情况下所得的估计误差为0.3199m。 图3(b)是三圆交于一个区域的情况， 所得椭球的中心点为[1.6236,1.7622]，因此误差为0.4452m。 图3(c)是三圆交于一点的情况，求出的椭球中心点为[1.6918,1.8376]，误差为0.3483m。

图3(a) 三圆不相交情况Fig.3(a) Three circles without intersection

图3(b) 三圆相交一个区域情况Fig.3(b) Three circles intersect

图3(c) 三圆相交一个点情况Fig.3(c) Three circles intersect at a point

总之，本文所提三边定位算法在各种情况下都可以求出包含真实状态的椭球，为之后的集员滤波算法提供了一个良好的基础。

5.2 集员滤波

考虑一个基于RSSI的室内动态目标跟踪系统，其状态方程为

xk+1=xk+ωk+uk

(58)

其中，uk=[0.1,0.1]T是控制输入；xk=[xk,yk]T是目标位置坐标；过程噪声ωk=0.05sin(k)。

第i个传感器的测量方程为

(59)

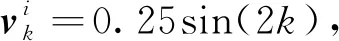
基于上述参数，在不使用锚节点切换方法前，使用本文提出的集员滤波估计目标位置的仿真结果如图4(a)和4(b)所示，使用锚节点切换后的估计椭球如图4(c)所示。估计误差用真实状态与估计椭球中心之间的距离差来表示。从图4可以看出，在使用锚节点切换与不使用锚节点切换两种情况下，目标真实状态都始终位于估计椭球中。从图5可以看出，随着目标逐渐远离初始传感器节点，无锚节点切换且只有三个锚节点的情况下椭球尺寸逐渐增大，当使用九个锚节点时，椭球尺寸比无锚节点切换情况下使用三个锚节点时的椭球尺寸小，但计算量大幅增加；而有锚节点切换的情况下，每次只使用三个锚节点的测量值就能使椭球尺寸比使用九个锚节点时小，且基本保持收敛。图6比较了有无锚节点切换情况下集员滤波算法与扩展Kalman滤波(Extended Kalman Filter, EKF)的误差。从图6可以看出，有锚节点切换时估计误差比其他两种情况都小，扩展Kalman滤波在噪声方差精确已知的情况下误差较小且比较稳定；但是当噪声方差不精确时误差比其他情况都大，而在实际中，很难获得精确的噪声方差，因此集员滤波算法更有优势。总体来看，锚节点切换可以以较小的计算成本使估计椭球收敛，且最后估计误差小于0.1m，因此选择有锚节点切换的情况更好。

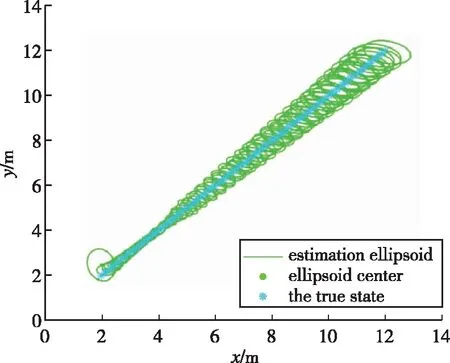
图4(a) 无锚节点切换时估计结果(三个锚节点)Fig.4(a) Estimation without switch of anchor(three anchors)

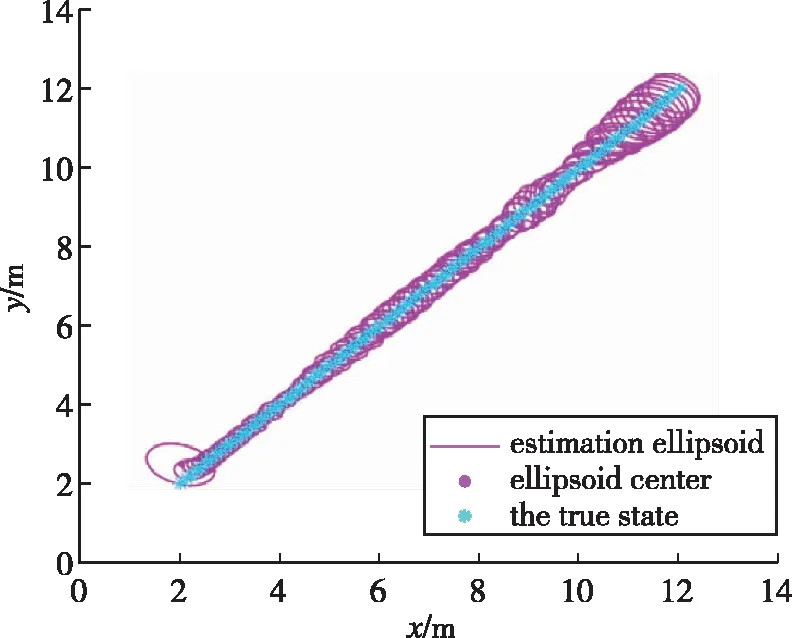
图4(b) 无锚节点切换时估计结果(九个锚节点)Fig.4(b) Estimation without switch of anchor(nine anchors)

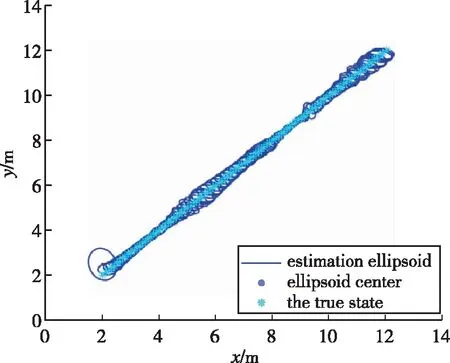
图4(c) 有锚节点切换时估计结果Fig.4(c) Estimation with switch of anchor

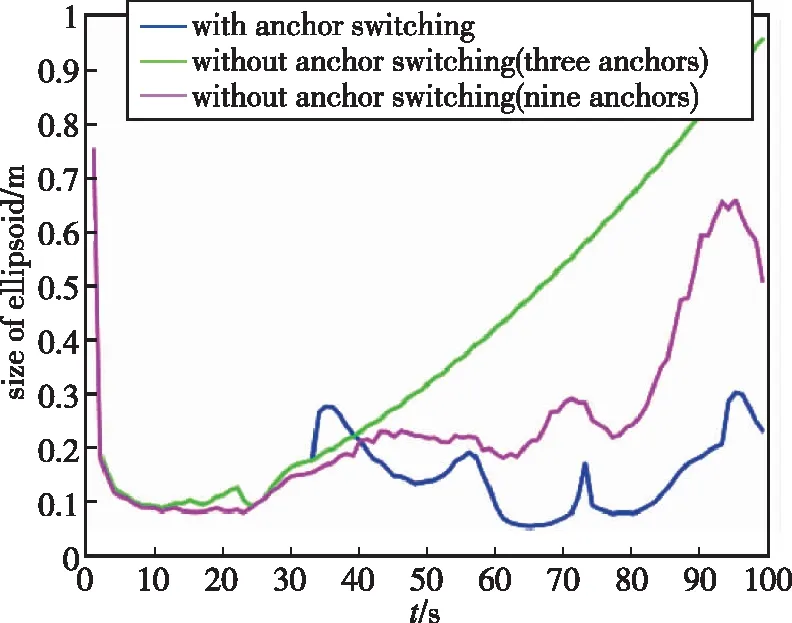
图5 椭球尺寸Fig.5 Size of ellipsoid

根据式(40)的触发条件可知，当目标移动较慢或静止不动时，两个相邻时刻的测量值变化幅度不大，可能达不到触发条件，因此可以降低传输频率。目标节点静止情况下，从k=1时刻到k=100事件触发的次数为11，移动情况下触发次数为92，由此可以得出，静止时触发频率较低，有效降低了传输与计算频率，节约了通信与计算资源。

图6 估计误差Fig.6 Error of estimation

6 结论

随着信息技术的发展，室内定位技术在基于位置服务相关的领域都占有举足轻重的地位，如何以有限的成本提供精确可靠的位置估计仍然是制约其发展的难题。为了提供可靠的位置估计，本文首先对三边定位算法进行了改进，随后引入基于事件触发的集员滤波估计移动目标位置，并针对实验过程中遇到的估计椭球不收敛问题提出了锚节点自主切换机制。算法分析与实验结果表明：

1)文中引入计算椭球并集最小外包椭球以及计算椭球交集最大内部椭球的算法改进了三边定位算法，使其在任何情况下都存在可行解。仿真结果表明，所提的改进的三边定位算法在传统三边定位算法无解的情况下仍可获得较满意的结果。

2)本文采用基于事件的集员滤波算法进一步降低了噪声影响，并提出了一种锚节点选择机制以克服估计椭球不收敛的问题，使用集员滤波可使定位误差小于0.1m。

3)事件触发机制可根据目标移动速度调节节点传输与计算频率，有效节约了传感网络的通信与计算资源。