一类时滞分数阶计算机病毒模型的稳定性研究
2021-04-16石剑平阮丽媛
石剑平,阮丽媛
(昆明理工大学理学院系统科学与应用数学系,云南 昆明650500)
1.引言
计算机病毒传播是网络安全中最为常见的问题,其传播速度快、范围广,带来的破坏性也非常大,不加以及时控制就会造成重大的经济损失,严重干扰社会生产的正常进行.因此,对计算机病毒传播机理问题进行研究非常必要,其中对于病毒传播模型的研究具有重要的理论和现实意义.1991年Kephart和White[1]注意到生物病毒传播与计算机病毒传播存在很多共性,首次将流行病学数学模型引入到计算机病毒传播的研究中.此后,众多学者也陆续使用生物学中的一些模型和分析方法对计算机病毒进行深入的研究.
分数阶模型最初是在数学基础理论的研究中提出的[2],因其计算的复杂性,在很长一段时间没有得到广泛的应用.随着计算机技术的发展,复杂的计算过程可以通过各种软件程序来完成,分数阶模型重新进入研究者的视野.由于分数阶微积分可以描述带有遗传属性的演化过程,其所具有的记忆特征不仅可以描述相关系统过去的状态,还会影响系统现在和未来的状态.近年来,数学、物理学、生物学、金融学等领域的研究者在各自的研究工作中均发现,某些问题采用分数阶模型来描述更能恰当的反映问题的真实情形.
“生态记忆”是生物种群模型的重要特征,它指的是“过去的状态或经验影响群落目前或未来反应的能力”[3],这一特征与分数阶微积分所能表现的特性不谋而合.很多研究者将分数阶微积分方法引入生物数学的各种模型中,获得了一批有理论价值和实际意义的结果.例如,Djordjevic等[4]采用分数阶常微分方程对一类细胞问题建模,模型与实际数据的吻合度比整数阶的模型更为准确;EI-Saka等[5]研究分数阶变动人口SIS 流行病模型,分析了平衡点的稳定性及一致稳态解的存在性条件;原三领等[6]则研究了一类分数阶SIR流行病模型的稳定性问题.基于流行病学的计算机病毒模型,因其演化过程和控制策略具有很强的“记忆”属性,采用分数阶微积分理论进行研究,可以获得诸如混沌等新的动力学特征[7].
本文将分数阶导数引入一类计算机病毒模型[8],考虑了三个因素对模型进行改进,且基于感染过程中病毒的潜伏性,提出了一个改进的时滞分数阶计算机病毒模型.采用文[9]总结的结论,从理论上分析模型的正平衡点处出现Hopf分支与时滞之间的联系.为了验证理论分析的合理性,选择恰当的系统参数进行数值模拟,并通过数值模拟获得分数阶变化的情况下时滞临界值的变化趋势.
2.模型描述
文[8]研究了一类计算机病毒模型(SIR模型):

其中,S(t),I(t),R(t)分别表示易感染节点、已感染节点和免疫节点的个数,0<α,β,γ,µ,θ <1是各种节点之间相互转化的概率.文[8]从信息传播机理出发,以上述系统作为信息传播的模型给出了信息传播的规则,建立了相应的平均场方程,并通过计算平衡点和基本再生数R0,从理论上证明了平衡点的渐近稳定性.
为了更准确地描述计算机网络系统病毒感染演化的过程,本文将分数阶导数引入模型(2.1),并进一步考虑三个因素对模型进行改进:第一,某些感染节点因系统的差异性,被感染后无法正常工作,因而退出整个网络系统;第二,有些易感节点因为软件的差异而具有先天免疫;第三,网络系统根据需要按一定的比例添加新的节点.由于某些计算机病毒的发作存在潜伏期,本文在易感染节点被感染的过程加入了时滞项.基于上述分析,我们建立以下时滞分数阶SIR模型:
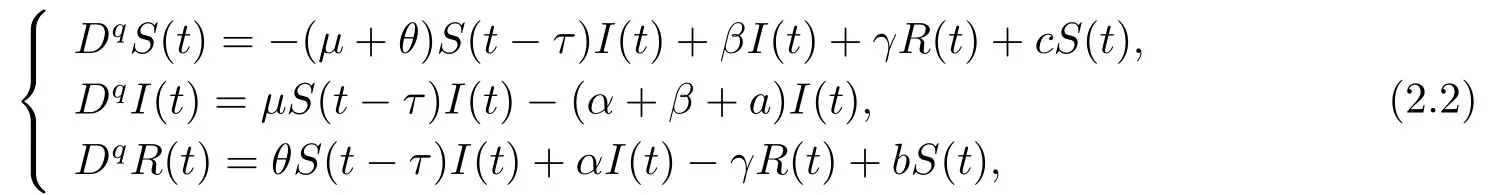
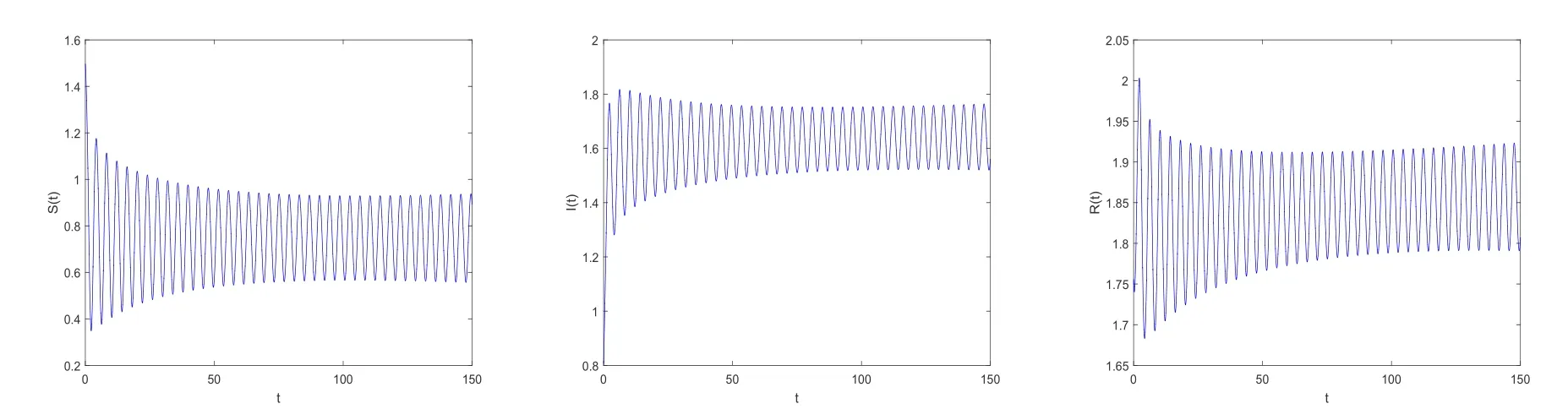
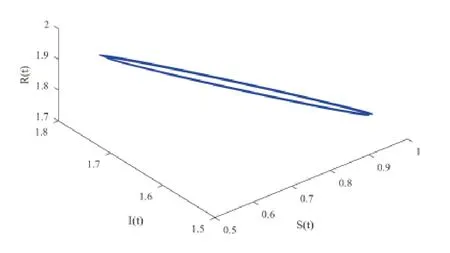
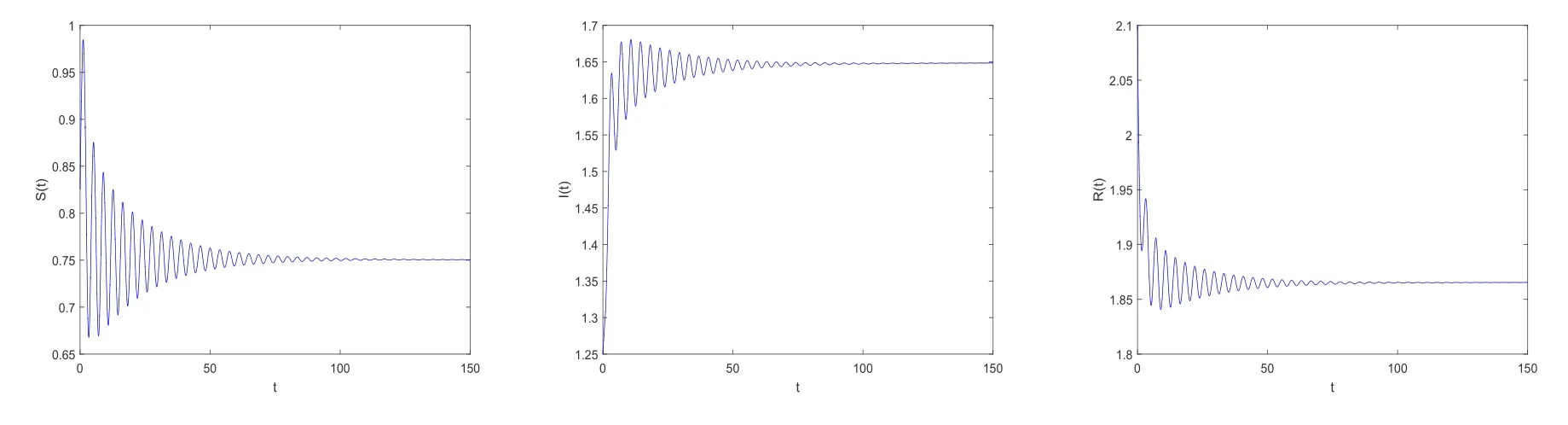
其中,q(0 模型(2.2)的平衡点为: 其中 根据上述模型假设,系统(2.2)是一个开放模型,在系统演化过程中有新的节点加入并有节点退出,所有的系统参数均取正值.显然平衡点E2的分量均不为零,此改进模型除了零平衡点和正平衡点外不存在无病平衡点,由于零平衡点的情况无实际意义,故下文仅研究正平衡点.为叙述方便,不妨假设正平衡点为E∗=(x∗,y∗,z∗),在E∗点对系统(2.2)做平移变换,变换公式为: 代入模型(2.2)得 研究分数阶微分方程系统的稳定性和Hopf分支问题,目前主要是基于其对应的线性化近似系统在平衡点处的稳定性来进行的.文[9]给出定义,说明系统的时滞τ满足以下三个条件,则在平衡点处会出现Hopf分支,即平衡点的稳定性可以由τ值来确定. 定义2.1[9]对于以下n-维分数阶时滞系统: 0<α ≤1 和τ ≥0.如果系统(2.4)满足以下三个条件: 1)当τ= 0,(2.4)在平衡点x∗= (x∗1,x∗2,...,x∗n)处的线性化系统的系数矩阵记为A,A的所有特征根λj(j=1,2,...,n)必须都满足 2)当τ=τ0时,(2.4)在平衡点x∗= (x∗1,x∗2,...,x∗n)处的线性化系统的特征方程存在一对纯虚根s(τ0)=±iω0; 3)横截条件 成立,其中s(τ)是(2.4)在平衡点x∗=(x∗1,x∗2,...,x∗n)处的线性化系统的特征方程的根,Re[·]指提取复数的实部. 则当时滞τ=τ0时,系统(2.4)在平衡点x∗=(x∗1,x∗2,...,x∗n)处出现Hopf分支. 注1定义2.1中,条件1)说明当时滞τ=0时,分数阶微分方程系统(2.4)在0<α<1时,分数阶数α可扩大模型的稳定区域,即当特征值穿过虚轴时,系统仍然可能稳定[10−11]. 下面将按照上述三个条件分析系统(2.2)正平衡点的稳定性. 将系统(2.3)在平衡点(0,0,0)处线性化,得到对应的线性化系统: 其中: Ⅰ 时滞为零时系数矩阵的特征根分析 当τ=0时,线性化系统(3.1)的系数矩阵对应的特征方程为 若特征方程(3.2)式满足Routh-Hurwritz条件,则所有的特征根均有负实部,因此,在给定参数条件下,只需验证以下三个不等式成立,即可保证定义2.1中的条件1)成立: Ⅱ 确定出现Hopf分支的时滞临界值 对(3.1)式做拉普拉斯变换[12]得到以下方程组: (3.4)式的特征方程为: 分离(3.5)式的时滞项和非时滞项可得: 其中 定义2.1的条件2)指出,要使分数阶系统在时滞临界值τ0处出现Hopf分支,其特征方程的根s必须是纯虚根.为了找到τ0,不妨假设s= iω=ω(cos(π/2)+i sin(π/2)),代入(3.6)式,分离实部与虚部可得到以下方程组: 其中M1,M2,N1和N2如下所示: 易求出 联立公式sin2(τω)+cos2(τω)=1可得到: 求解上式可得ω.设ωi(i=0,1,2,...)为ω中所有的正值,代入(3.9)式计算sin(τω)和cos(τω),可得到τ的计算公式如下所示: (I)如果W1(ωi)>0,W2(ωi)>0,则 (II)如果W1(ωi)<0,W2(ωi)>0,则 (III)如果W1(ωi)>0,W2(ωi)<0,则 (IV)如果W1(ωi)<0,W2(ωi)<0,则 按照时滞的实际意义,我们仅考虑其最小正值,取 根据定义,τ=τ∗0即为系统(2.3)出现Hopf分支的时滞临界值,对应于τ∗0的ω值记为ω∗0=ωi. Ⅲ 验证横截条件 在文[9]中,通过对特征方程两边求τ的一阶偏导数,推导了的计算公式,但此公式比较复杂,由此给出的判断横截条件的假设较为严格.文[13]通过构造辅助函数,提出了一种更为恰当的判断方法,下面采用文[13]提出的判别方法验证横截条件. 将s=iω带入(3.6)式,则不妨令 构造以下的辅助函数: 定义Jacobi行列式为: 综上分析,我们得到以下结果: 定理3.1对于系统(2.3),在给定参数组(α,β,γ,µ,θ,a,b,c)的情况下,如果以下假设成立: (H1)(3.3)式成立; (H2)当τ=τ∗0时,系统(2.3)在平衡点(0,0,0)处的线性化系统的特征方程(3.5)存在一对纯虚根s=±iω∗0; (H3)J(ω∗0,τ∗0)>0,J(ω,τ)为(3.11)式和(3.12)式所定义的Jacobi行列式.则当时滞τ=τ∗0时,系统(2.3)在平衡点(0,0,0)处出现Hopf分支. 注2由定理3.1即可推出,当时滞τ=τ∗0时,系统(2.2)在正平衡点E∗= (x∗,y∗,z∗)处出现Hopf分支. Ⅰ 平衡点的稳定性模拟 为了验证上述理论分析结果的正确性,选择一组恰当的参数α=0.2,β=0.2,γ=0.4,µ=0.6,θ= 0.3,a= 0.05,b= 0.06,c= 0.05代入模型(2.2),正平衡点E∗= (0.75,1.65,1.865625),分数阶取值为q= 0.9,计算得时滞临界值为τ∗0= 0.981197,对应的ω∗0= 1.620917262,容易验证(3.3)式成立,且J(ω∗0,τ∗0)>0.为了更好的展示理论分析的结果,我们选择两种情况,借助于文[14]给出的预估校正法做数值模拟.一种情况为τ= 0.99>τ∗0= 0.981197,模拟结果见图4.1和图4.2,此时正平衡点出现Hopf分支,是不稳定的.另一种情况为τ= 0.93<τ∗0=0.981197,模拟结果见图4.3和图4.4,显然此时正平衡点是渐近稳定的. 图4.1 模型(2.2)状态变量的波形图,初值为(1.5,0.8,1.75), q =0.9, τ =0.99>0.981197,正平衡点不稳定 图4.2 初值为(1.5,0.8,1.75), q =0.9, τ =0.99>0.981197,模型(2.2)在正平衡点处出现Hopf分支 图4.3 模型(2.2)状态变量的波形图,初值为(0.822,1.25,2.1), q = 0.9, τ = 0.93 < 0.981197,正平衡点是渐近稳定的 图4.4 初值为(0.822,1.25,2.1), q =0.9, τ =0.93<0.981197,模型(2.2)的正平衡点是渐近稳定的 Ⅱ 分数阶对时滞临界值的影响 通过上述理论分析和数值模拟可知,对于有病毒传染的计算机网络系统,在模型参数给定的情况下,系统从不稳定状态进入稳定状态,病毒潜伏到发作的时间需要控制在一定的时间范围τ <τ∗0.反之,在知道病毒的潜伏期,即已知τ的情况下,如果需要控制系统的稳定状态,就需要对系统进行干扰以改变时滞临界值τ∗0,即改变稳定域的大小.此时,需要对影响τ∗0的因素进行分析. 影响时滞临界值的因素非常多,从时滞临界值的计算公式来看,模型参数、分数阶都是影响时滞临界值大小,继而影响系统稳定性的直接因素.本文以分数阶为参数,不改变前面模型(2.2)参数的取值,通过数值模拟获得模型导数从整数阶到分数阶、分数阶不断减小的过程中,时滞临界值的具体变化情况,详见表4.1. 表4.1说明,模型的导数从1到0.8的变化过程中,时滞临界值τ∗0随着q值的减小不断增加.在0.8至0.75之间的某一点处,τ∗0的变化发生转折,不再随着q值的减小而增加,反而随着q值的减小而不断变小.由此可见,通过改变分数阶的大小改变时滞临界值,是可以影响系统的稳定域的. 表4.1 分数阶的变化对ω∗0 和τ∗0 的影响 本文根据病毒的演变特征和潜伏特征,引入分数阶导数和时滞项对一类计算机病毒模型进行了推广.采用线性化方法和拉普拉斯变换对模型进行转换,通过分析线性化系统的系数矩阵特征方程和系统特征方程,分析了时滞和分数阶系统平衡点稳定性之间的关系,推导了Hopf分支出现时时滞临界值的计算公式.为了验证理论分析的合理性,选择恰当的系统参数进行数值模拟,模拟结果不仅验证了结论的正确性,还揭示了分数阶对时滞临界值的影响趋势.本文的研究结果一定程度上推广了计算机病毒模型的研究范围和方法.
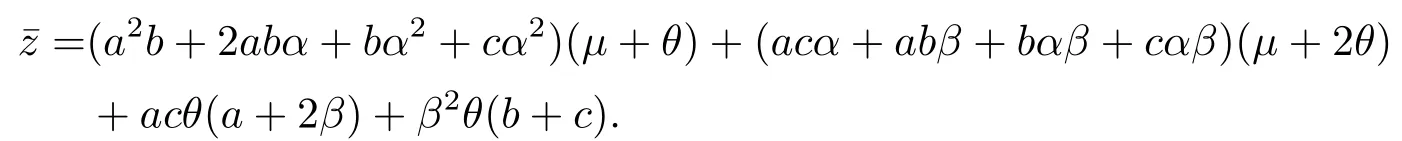
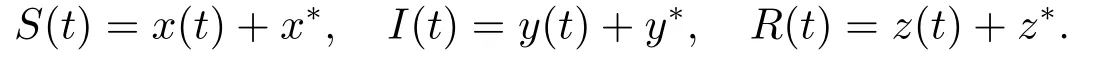
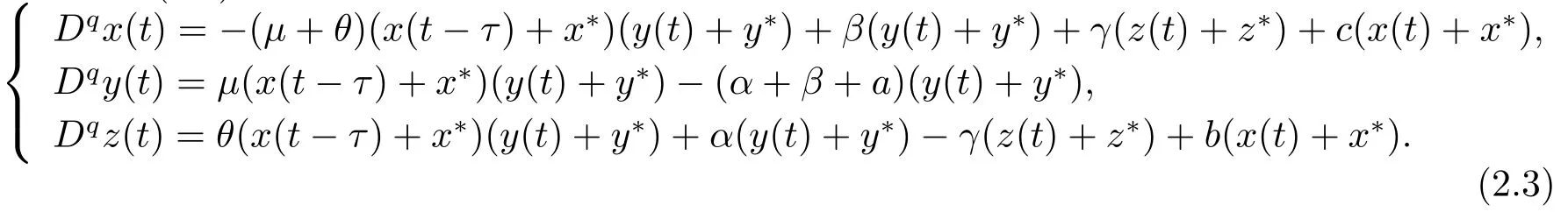


3.Hopf分支分析
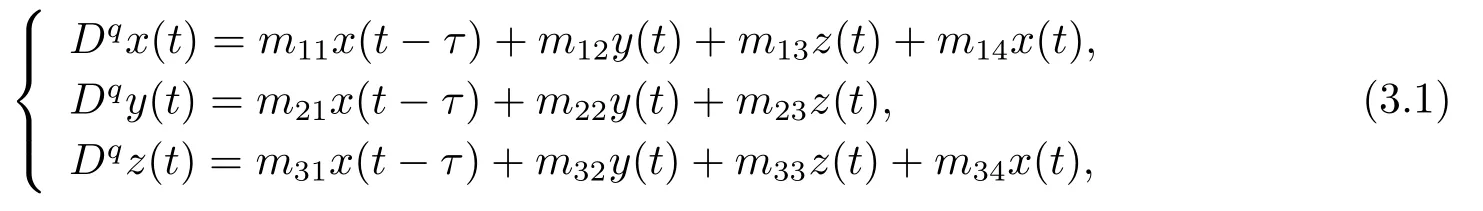
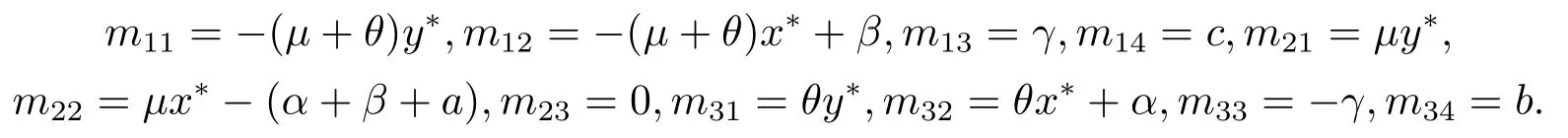
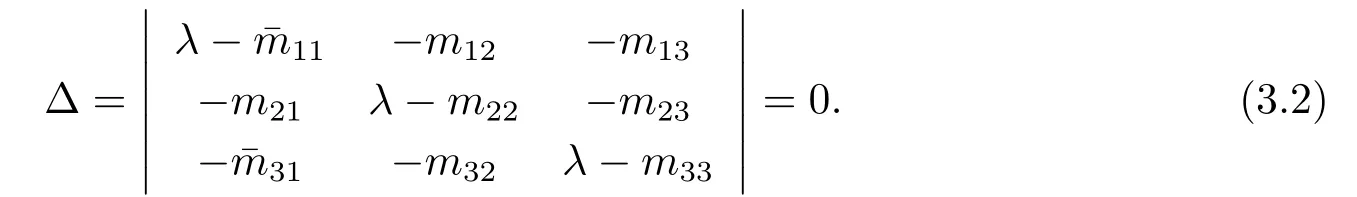
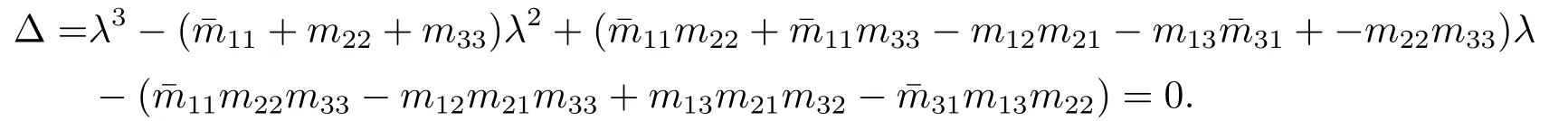

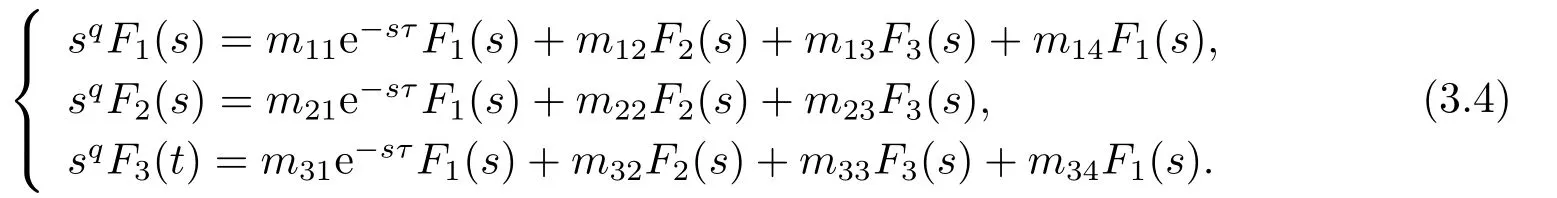
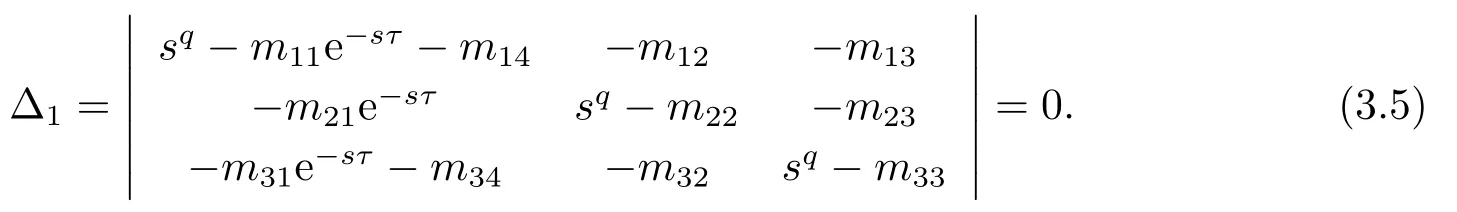

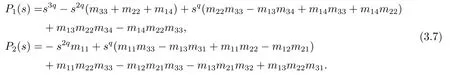
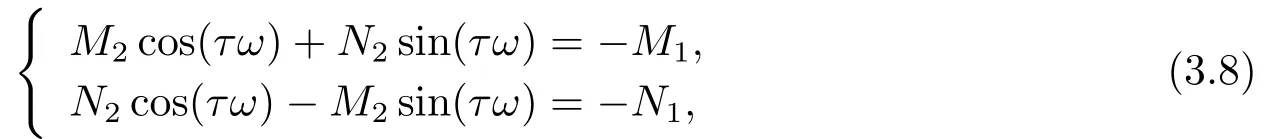
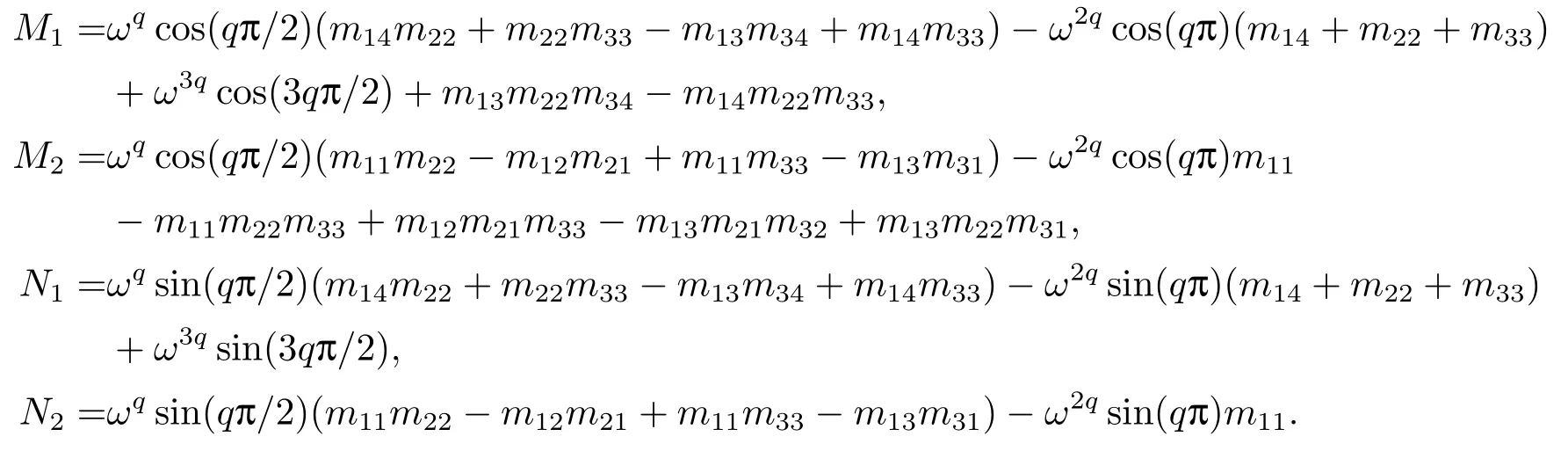
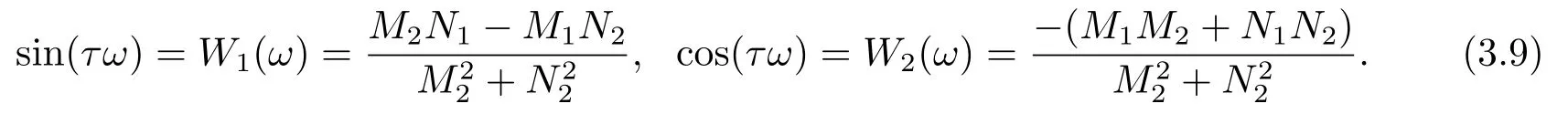
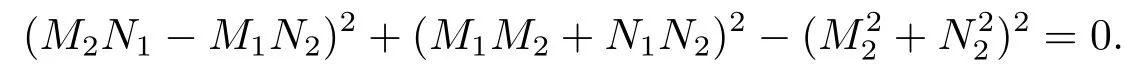


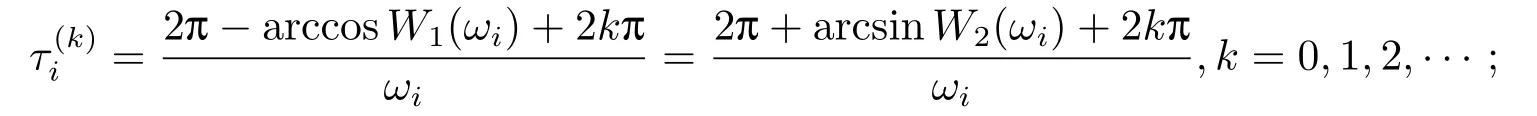
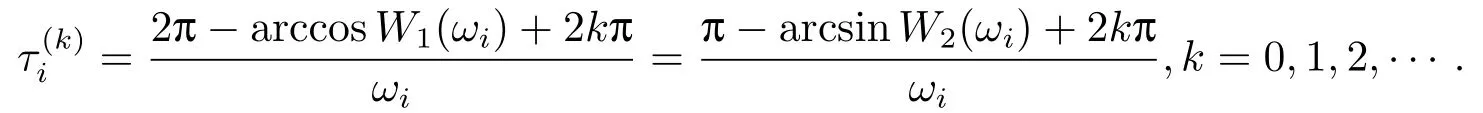
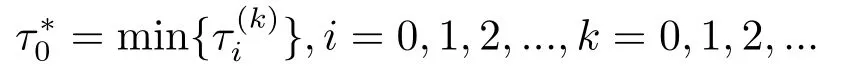
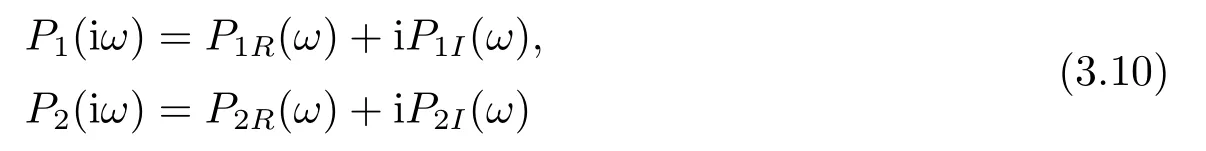
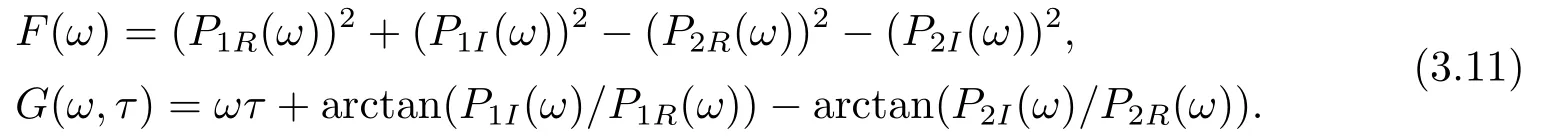

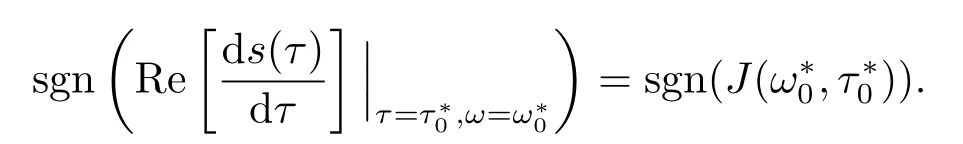
4.数值模拟


5.结语
