Limit Cycles Appearing from a Perturbed Differential System with m Switching Lines

YANG Jihua(杨纪华),YAN Jie(闫洁),ZANG Xiaofang(臧小芳)

(School of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,China)

Abstract: In this paper,we deal with the number of limit cycles of a perturbed differential system with m switching lines.One of the key points of our approach is that we obtain the algebraic structure of the first order Melnikov function M(h)by computing its generators,and this method can be applied to study the number of limit cycles of other perturbed differential systems with multiple switching lines.

Key words: Switching line;Limit cycle;Melnikov function

1.Introduction

Probably the main open problem in the qualitative theory of real planar differential systems is the determination and distribution of their limit cycles.A classical way to produce limit cycles is by perturbing a system which has a center,in such a way that limit cycles bifurcate in the perturbed system from some of the periodic orbits of the center for the unperturbed system.It is well known that perturbing the linear center

by arbitrary polynomialsf(x,y)andg(x,y)of degreen,i.e.

we can obtain up to the first order inεat mostbifurcated limit cycles,where[·]denotes the integer part function.[1]

Stimulated by discontinuous phenomena in the real world,there have been many works focused on the study of limit cycle problem for piecewise smooth differential systems that the phase space is divided into two disjoint connected subregions byx=0 ory=0.For example,LIU and HAN[2]established the first order Melnikov function formula for planar piecewise smooth Hamiltonian systems with a switching linex= 0 which plays a crucial role in the study the number of limit cycles.By using this formula,they obtained the maximal number of limit cycles of the following perturbed system

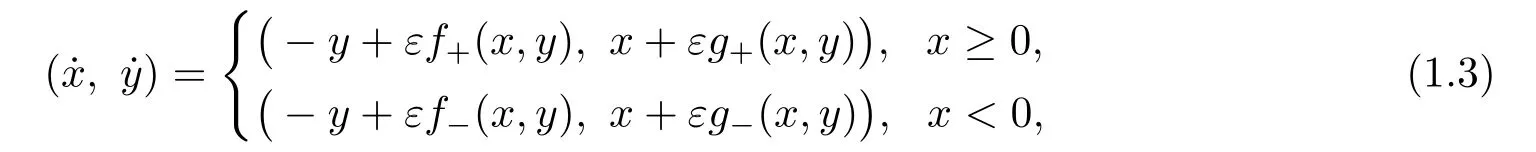
wheref±(x,y)andg±(x,y)are polynomials inxandyof degreen.For more results,one can see [3-6] and the references quoted there.

However,as pointed out in [7],discontinuities may occur on multiple lines or even on nonlinear curves or surfaces.Recently,there are some works studying the piecewise smooth differential systems with multiple switching lines.[8−12]For example,HU and DU[9]discussed the bifurcations of periodic orbits of perturbed planar discontinuous system with discontinuities on the switching linesL1,L2,···,Lm:

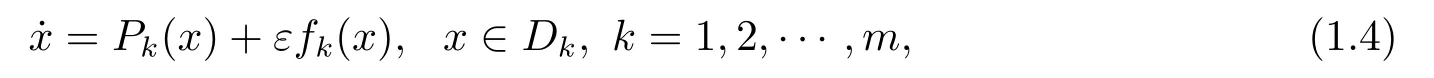
where 0<|ε|≪1,Pk(x),fk(x)∈C2Dk ∪Lk ∪Lk+1,Lk={x ∈R2:cTk x=0}is a half-line starting at the origin,ck ∈R2is a constant vector satisfying∥ck∥=1,Dkis the open region betweenLkandLk+1fork= 1,2,··· ,mandL1=Lm+1.The authors gave the first order Melnikov function,denoted byM(h),which can be used to study the number of limit cycles of system (1.4).As an application,they presented a piecewise cubic system with 4 switching lines.

In this paper,motivated by the above results,we will use the first order Melnikov function given in [9] to study the number of limit cycles of system (1.1)under the perturbations of discontinuous polynomials of degreenwithmswitching lines.More precisely,we consider the following piecewise smooth differential system

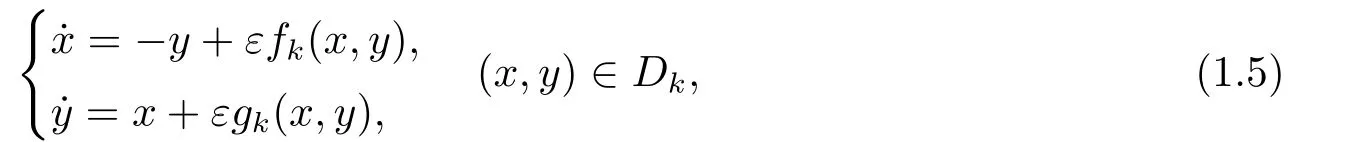
where 0<|ε|≪1,Lk:τkx+σky=0 is a half-line starting at the origin satisfyingτ2k+σ2k=1 andσk ≥0,Dkis the open region betweenLkandLk+1fork= 1,2,··· ,m,m ≥2 andL1=Lm+1,

A first integral of system (1.5)|ε=0is

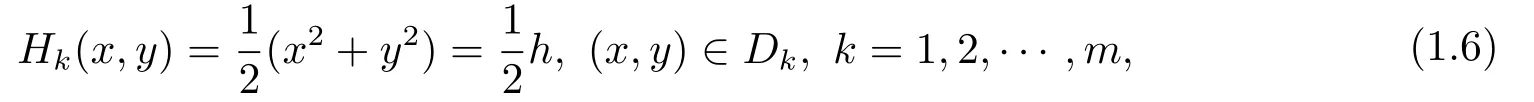
withh ∈(0,+∞).Whenε=0,(1.5)has a family of periodic orbits as follows

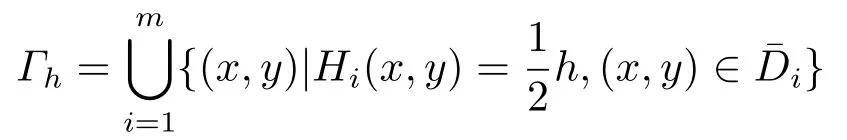
withh ∈(0,+∞).Ifh →0,Γhapproaches the origin which is an elementary center.See Fig.1 for illustration.

Fig.1 The phase portrait of system (1.5)|ε=0

Our main result is the following theorem.

Theorem 1.1Consider the system (1.5)with|ε|small enough.Using the first order Melnikov function,the maximal number of limit cycles which bifurcate from the periodic annulus of the origin of system (1.5)|ε=0isn.Moreover,the corresponding upper bound is reached for suitablefk(x,y)andgk(x,y).

Remark 1.1From Theorem 1.1,we know that the numberm ≥2 of switching lines does not affect the number of limit cycles which bifurcate from the period annulus of the origin of system (1.5)|ε=0.

Remark 1.2In this paper,a method for calculating the first order Meilnikov function of a perturbed polynomial differential system with multiple switching lines is presented and this method can reduce a lot of computations.

2.Proof of Theorem 1.1

From Theorem 2.2 in [9] and Remark 2.3 in [12],we know that the first order Melnikov functionM(h)of system (1.5)has the following form

By Theorem 2.3 in [9],we know that the number of zeros of the first order Melnikov functionM(h)controls the number of limit cycles of systems (1.5)withε= 0 ifM(h)0 in the corresponding period annulus.

Forh ∈(0,+∞)andi,j ∈N,we denote

wherekinIki,j(h)is a superscript.We first derive the algebraic structure of the first order Melnikov functionM(h)defined by (2.1).

Lemma 2.1Forh ∈(0,+∞),

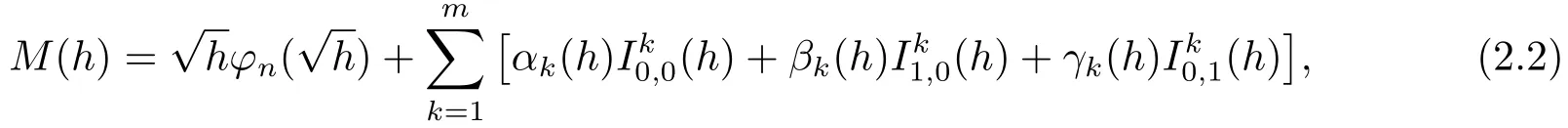
whereφn(u)is a polynomial inuof degreen,andαk(h),βk(h)andγk(h)are polynomials ofhwith

ProofLetΩbe the interior of(see Fig.1).Using the Green’s Formula,we have

By a straightforward computation and noting thatσk ≥0,we have

Hence,by (2.1),(2.3)and (2.4),we obtain

whereφkn(u)are polynomials inuof degree at mostnandλki,jare arbitrary constants fork=1,2,··· ,m.

In the following,we should prove that

whereψkn(u)are polynomials inuof degree at mostn,αk(h),βk(h)andγk(h)are polynomials ofhwith

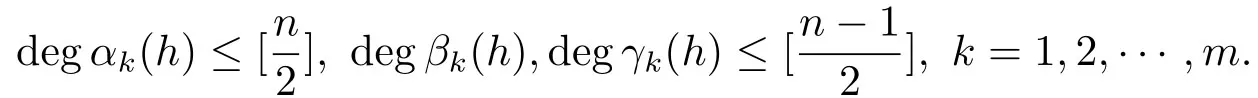
Without loss of generality,we only prove the casek= 1,and the other cases can be proved in a similar way.

Differentiating the equation (1.6)with respect toxfork=1,we obtain

Multiplying (2.6)byxi−1yjdxand integrating overwe have

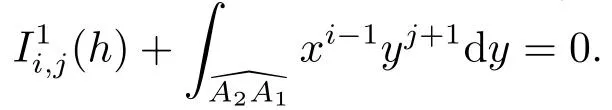
In view of (2.3)and (2.4),we have

whereδ1i,jis a constant.Hence,

Similarly,multiplying the first equation in(1.6)byxiyj−2dyand integrating overyields

Elementary manipulations reduce Eqs.(2.7)and (2.8)to

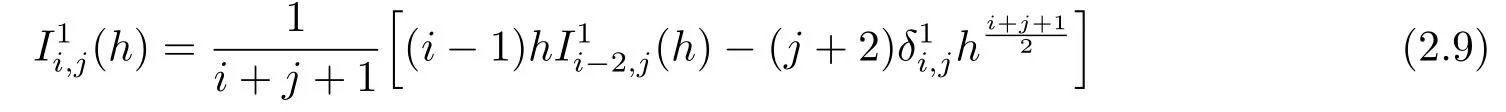
and

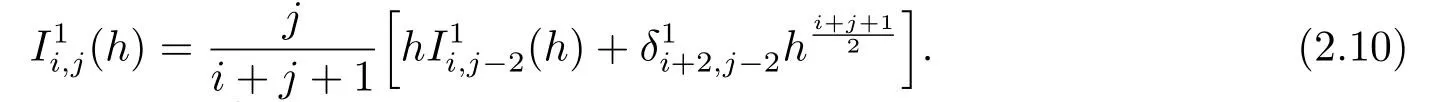
We will prove the conclusion by induction onn.It is straightforward from (2.9)and(2.10)to show that

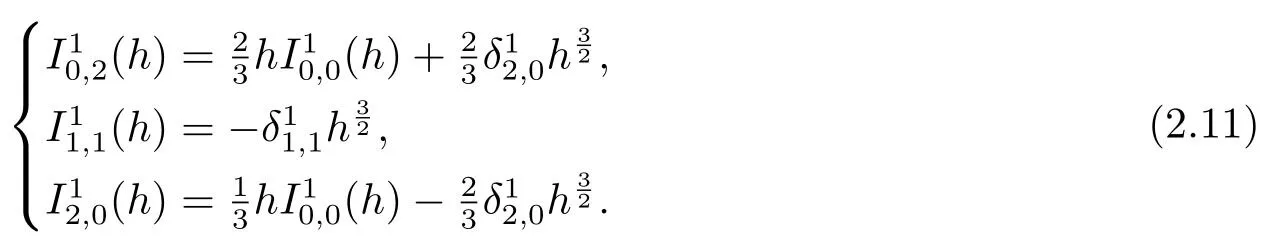
Thus,(2.5)holds forn=2.Now suppose that(2.5)holds for alli+j ≤n−1,then fori+j=n,taking (i,j)=(0,n),(1,n −1),(2,n −2),··· ,(n −2,2)in (2.10)and (i,j)=(n −1,1),(n,0)in (2.9),respectively,we obtain

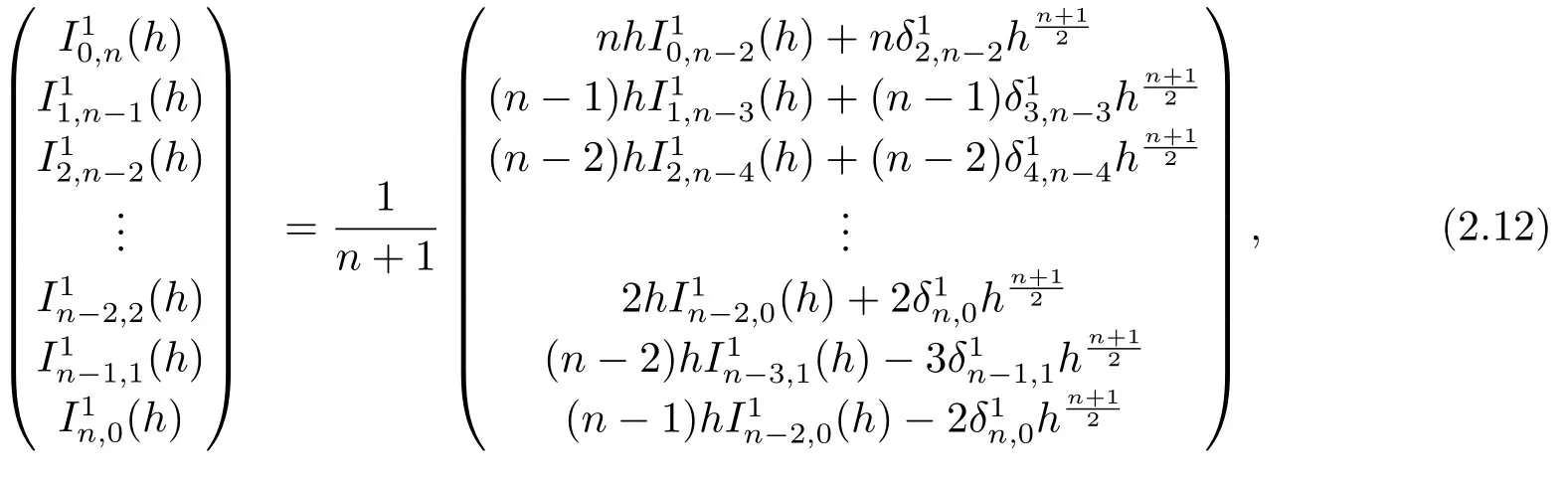
which implies that(2.5)holds fori+j=n.Moreover,in view of(2.12),we have fori+j=n

whereδis a constant andα1n−2,β1n−2(h)andγ1n−2(h)represent the polynomials inhsatisfying

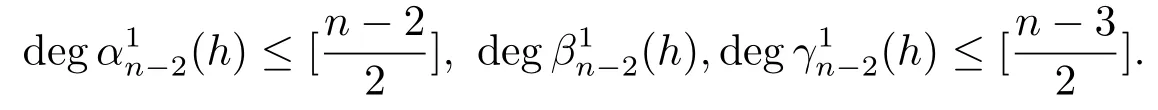
It is easy to check that

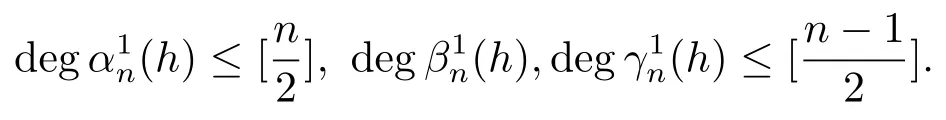
This ends the proof.

Remark 2.1The method which we use to obtain the algebraic structure of the first order Melnikov functionM(h)in Lemma 2.1 is more simple than the way to computeM(h)directly.

Lemma 2.2Forh ∈(0,+∞),

whereψ(h)is a polynomial inhof degreeandφn(u)is a polynomial inuof degreen.

ProofFrom Lemma 2.1,we have

whereφn(u)is a polynomial inuof degreen,andαk(h),βk(h)andγk(h)are polynomials ofhwith

By easy calculations and noting that

we have

whereC,ak,bkandckare constants.Substituting (2.15)into (2.14)gives (2.13).This ends the proof.

In the following,we denote by #{ϕ(h)=0,h ∈(λ1,λ2)}the number of isolated zeros ofϕ(h)on (λ1,λ2),taking into account the multiplicity.

Proof of Theorem 1.1LetThen,from Lemma 2.2,we have

To show thatnzeros can appear,we choosefk(x,y)≡0,gl(x,y)≡0 fork=1,2,··· ,mandl=2,3,··· ,m.Then,(2.1)becomes