泊松逆高斯回归模型的贝叶斯统计推断

赵远英,徐登可,冉庆

(1.贵阳学院数学与信息科学学院,贵州 贵阳550005;2.浙江农林大学统计系,浙江 杭州311300;3.贵阳市第七中学数学组,贵州 贵阳550001)

1.引言

计数数据[1]广泛存在于自然科学领域和社会科学领域,泊松回归模型是刻画计数型响应变量与协变量之间关系常用的统计工具,但在实际应用时由于计数数据的复杂性,数据和泊松回归模型经常不相吻合,偏大离差或偏小离差等情形时常发生,这与泊松回归模型响应变量的条件均值与方差相等这一基本要求相违背.因此许多其他的计数层次回归模型被提出来解决上述不足.例如:负二项回归模型[2],泊松对数正态模型[3],混合泊松回归模型[4],广义泊松回归模型[5]等.特别地,XIE和WEI[6]基于EM算法研究泊松逆高斯回归模型的影响诊断问题;解锋昌等[7]比较系统全面地阐述零膨胀数据的统计方法和应用价值.有关计数数据建模及其其它更多统计方法,请参考LIU,TANG和XU[8]等文献.虽然在计数层次回归模型及其方法方面已经取得丰硕的研究成果,然而鲜有文献研究泊松逆高斯回归模型在贝叶斯框架下的统计推断问题.因此,本文旨在贝叶斯统计和泊松逆高斯回归模型的框架背景下:1)估计模型的未知参数;2)评估模型的拟合优度.

文章的结构见下:第2部分将泊松逆高斯分布看作逆高斯分布的泊松混合,定义泊松逆高斯回归模型;第3部分将服从逆高斯分布的随机变量视为缺失数据,使用数据添加的思想并基于Gibbs抽样[9]和Metropolis-Hastings算法[10-11]以及Multiple-Try Metropolis算法[12]详细描述模型未知参数的贝叶斯估计与贝叶斯拟合优度统计量的计算过程,处理算法中包含的高维积分问题;第4部分是模拟研究和实证分析;本文的结论在第5部分;附录部分是抽样算法的具体细节.

2.泊松逆高斯回归模型及其假设

与文[13-14]类似,本文关注泊松逆高斯回归模型:

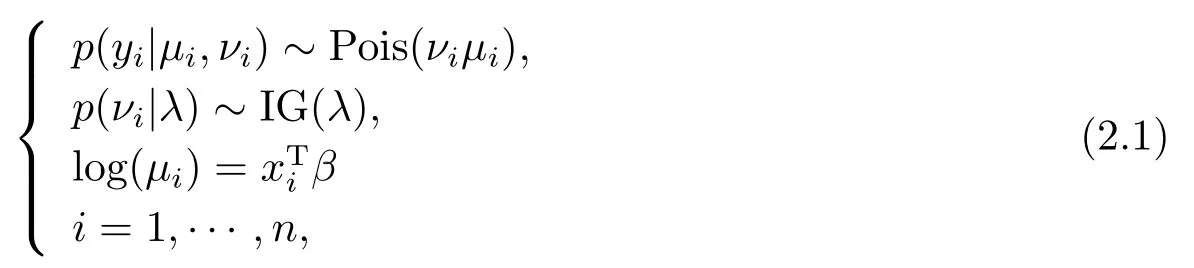
其中符号p(νi|λ)∼IG(λ)表示随机变量νi服从逆高斯分布IG(λ),其概率密度函数为

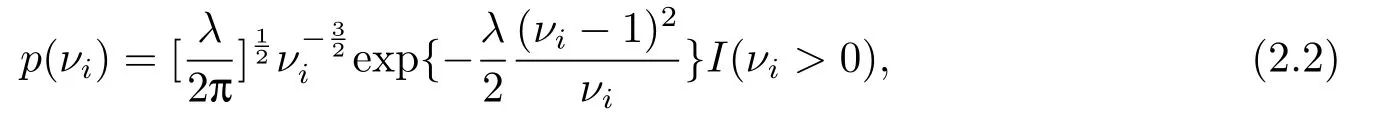
这里I(·)是示性函数.因此E(νi)= 1,Var(νi)=λ1.而p(yi|νi,µi)∼Pois(νiµi)表示在νi和µi给定的条件下,响应变量yi服从参数为νiµi的泊松分布,即E(yi|νi,µi)= Var(yi|νi,µi)=νiµi.在模型(2.1)中,log(µi)=xTi β表明参数log(µi)与p×1协变量xi存在线性关系,β=(β1,··· ,βp)T是未知参数向量.上述泊松逆高斯分布可视为逆高斯分布的泊松混合[14].下面将在贝叶斯统计和泊松逆高斯回归模型的框架下研究模型的参数估计问题和拟合优度检验问题.

3.模型的贝叶斯统计推断

记θ=(βT,λ)T,本文假设θ的先验分布为:

且

其中N(β0,Hβ)表示期望为β0,协方差矩阵为Hβ的正态分布,Γ(a,b)代表参数为a与b,期望为的伽玛分布,β0,Hβ,a,b是给定的超参数.

记y={y1,y2,··· ,yn},x={x1,x2,··· ,xn}和潜变量ν={ν1,ν2,··· ,νn},并记观测数据Z={y,x}.对参数θ的贝叶斯统计推断可以基于θ关于观测数据Z的后验分布p(θ|Z)∝p(Z|θ)p(θ),其中是观测数据Z的似然函数.显然上述积分无解析表达式.为了处理上述高维积分问题,借助数据添加[15]的思想,本文将潜变量ν视为缺失数据,考虑参数θ基于完全数据{Z,ν}的后验分布:

(3.3)式的优势在于不涉及高维积分的计算,但是直接从(3.3)式中抽样是不可能实现的.因此在这里借助Gibbs抽样[9]方法获得分布p(θ,ν|Z)的随机样本(θ,ν),然后基于此随机样本对参数θ作相应的贝叶斯统计推断.比如,参数g(θ)的贝叶斯后验期望估计为

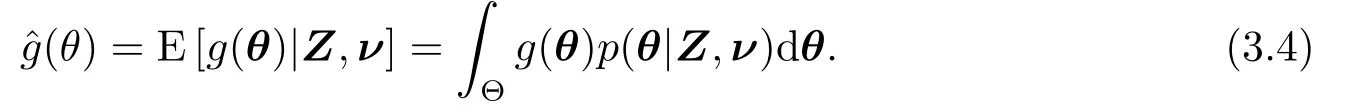
步1初始化β与λ以及ν,使它们的初始值分别为β(0)和α(0)以及ν(0)= (ν1(0),··· ,νn(0))T,并令t=0;

步2从p(β|y,ν(t),x,λ(t))中抽样β(t+1);这里

步3 从p(λ|y,ν(t),x,β(t+1))中抽样λ(t+1);其中即

步4∀i=1,··· ,n,从p(νi|yi,xi,β(t+1),λ(t+1))中抽样ν(t+1)i;这里

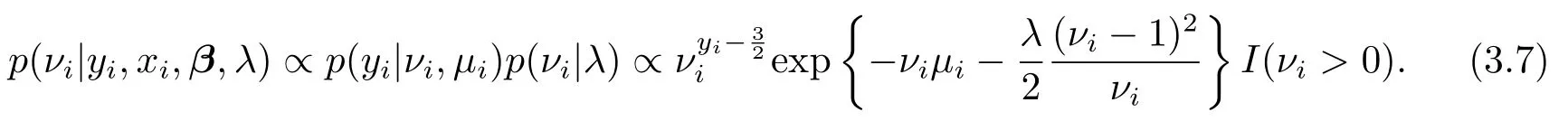
步5 令t=t+1,循环执行步2到步4直至算法收敛后,获得需要的随机样本.

本文在抽样的过程中采用Metropolis-Hastings算法[10-11]以及Multiple-Try Metropolis算法[12],细节见附录部分.

类似于文[16-17],可得未知参数θ与潜变量ν的联合贝叶斯估计为:

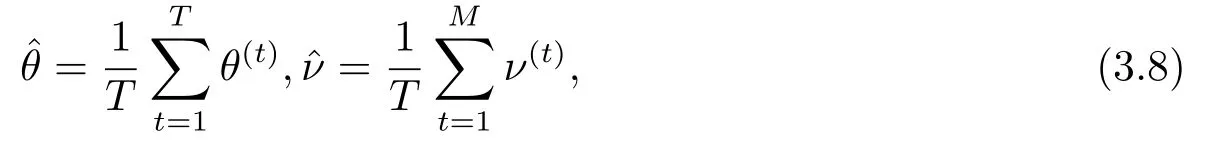
其中{(θ(t),ν(t)):t=1,··· ,T}是Gibbs抽样方法收敛后从p(θ,ν|Z)中获得的样本,且由(3.8)式表示的贝叶斯估计是其相应后验均值的相合估计[18].

为了评估贝叶斯统计框架下所研究模型是否合理,后验预测p值[19]和偏后验预测p值[20]是评估模型拟合优度检验的常用统计量.本文考虑以下的假设检验问题H0:数据{y,x}来自于由(2.1)式定义的泊松逆高斯回归模型;H1:H0不成立.类似于Gelman,MENG和Stern[21]的研究,定义泊松逆高斯回归模型的后验预测p值为

这里yrep表示y的一个重抽样值,Pr代表在y,x已知和H0成立的条件下,关于(θ,ν)的联合后验分布求条件概率,其表达式为

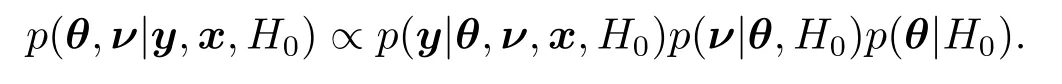
偏差度函数D(·|·)取为

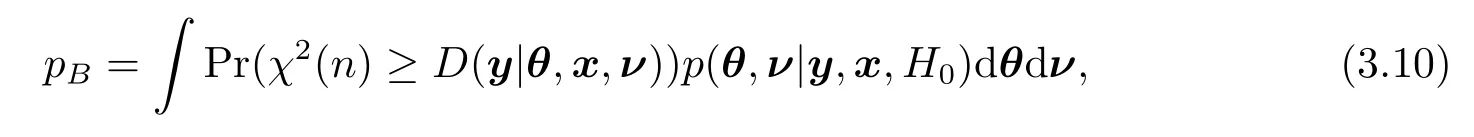
其中{(θ(t),ν(t)):t= 1,...,T}是产生于P(θ,ν|y,x,H0)的随机样本,这些随机样本与(3.8)式的样本相同.值得注意的是,(3.11)式中的散度函数D(y|θ(t),x,ν(t)))很容易计算,而χ2分布的分位数可以使用通常的统计软件获得,故(3.11)式的计算很容易完成.与文[16]相类似,当∈(0.3,0.7)时,逆高斯回归模型(2.1)对数据的拟合效果很好;否则,模型(2.1)对数据的拟合效果不理想.

类似于文[20-21]的研究,将模型(2.1)中的ν视为缺失数据,定义泊松逆高斯回归模型的偏后验预测p值为(3.12)式表示Pr{D(y|θ,x,ν)≥D(yobs|θ,x,ν)}关于分布p∗(θ,ν)求期望,其中yobs为响应变量y的观测值,

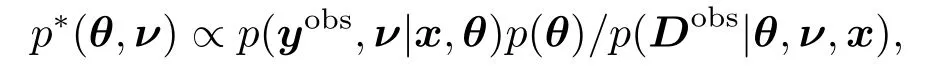
Dobs是D(·|·)基于yobs的观察值.易知在给定θ,x,ν的条件下,Dobs近似服从自由度为n的χ2分布.因此(Dobs|θ,x,ν)条件独立于θ,ν,从而可得

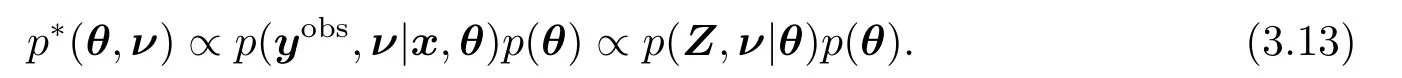
因为(3.12)式含有难以处理的积分问题,Monte Carlo方法被用来解决这一困难.记{(θ(t),ν(t)):t=1,...,T}是来自p∗(θ,ν)的随机样本(恰为(3.8)式所述),{y(t):t=1,...,T}是来自p(y|θ(t),x,ν(t))的随机样本.则由Monte Carlo积分原理,偏后验预测p值pppB的估计为

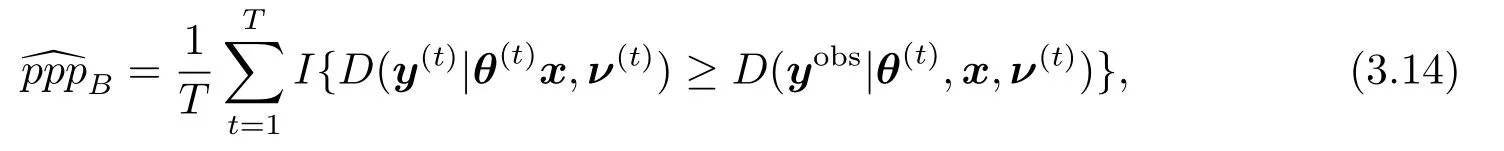
其中I(.)是示性函数.与文[22]相类似,若的值远离0.5,则认为H0不真.

4.数值例子

∀i=1,··· ,n,假设yi产生于(2.1)式定义的泊松逆高斯回归模型,νi与µi分别由下面的模型产生:

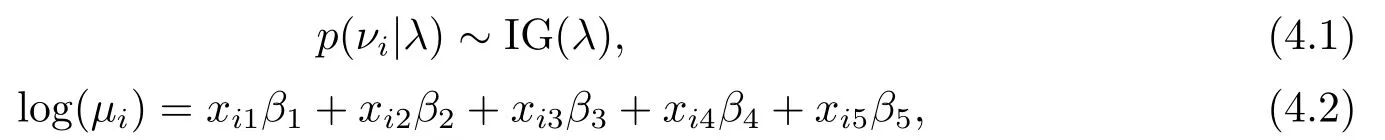
协变量xi= (xi1,xi2,xi3,xi4,xi5)T的每一分量都分别独立从均匀分布U(−1,1)中产生,设置参数的真值为下面两种情形:

情形1β=(β1,β2,β3,β4,β5)T=(1,1,1,1,1)T和λ=1;

情形2β=(β1,β2,β3,β4,β5)T=(1,1,1,1,1)T和λ=2.

本文分别研究n=100与n=200两种情形的模拟数据样本,同时考虑以下两种类型的先验分布对贝叶斯估计方法的影响:

Type 1(良好的先验)β0取为β的真值,Hβ=0.25I5和a=b=1,其中0.25Im表示主对角元素为0.25的m×m对角矩阵.

Type 2(无信息先验)β0=(0,0,0,0,0)T,Hβ=10I5和a=b=1.

本文从MCMC算法收敛[23]后的Gibbs抽样中收集4000个随机样本用来计算(3.8)式未知参数和潜变量的联合贝叶斯估计.表1和表2是重复模拟100次的相关计算结果,其中Mean,Median,5%th,95%th和SD分别表示100次重复基础上得到的贝叶斯估计的均值,中位数,5%和95%样本分位数和样本标准差,RMS代表参数真值与100次重复的贝叶斯估计的均方根.根据表1不难得出:(i)对先验分布中超参数的不同选择,估计结果都比较稳健,且在第一种先验类型条件下的贝叶斯估计略优于第二种类型先验下的贝叶斯估计;(ii)两种先验类型条件下的Mean和Median与参数真值都非常接近,说明该估计方法具有很高的估计精度;(iii)贝叶斯估计方法的性能伴随着n的变大越来越稳定.

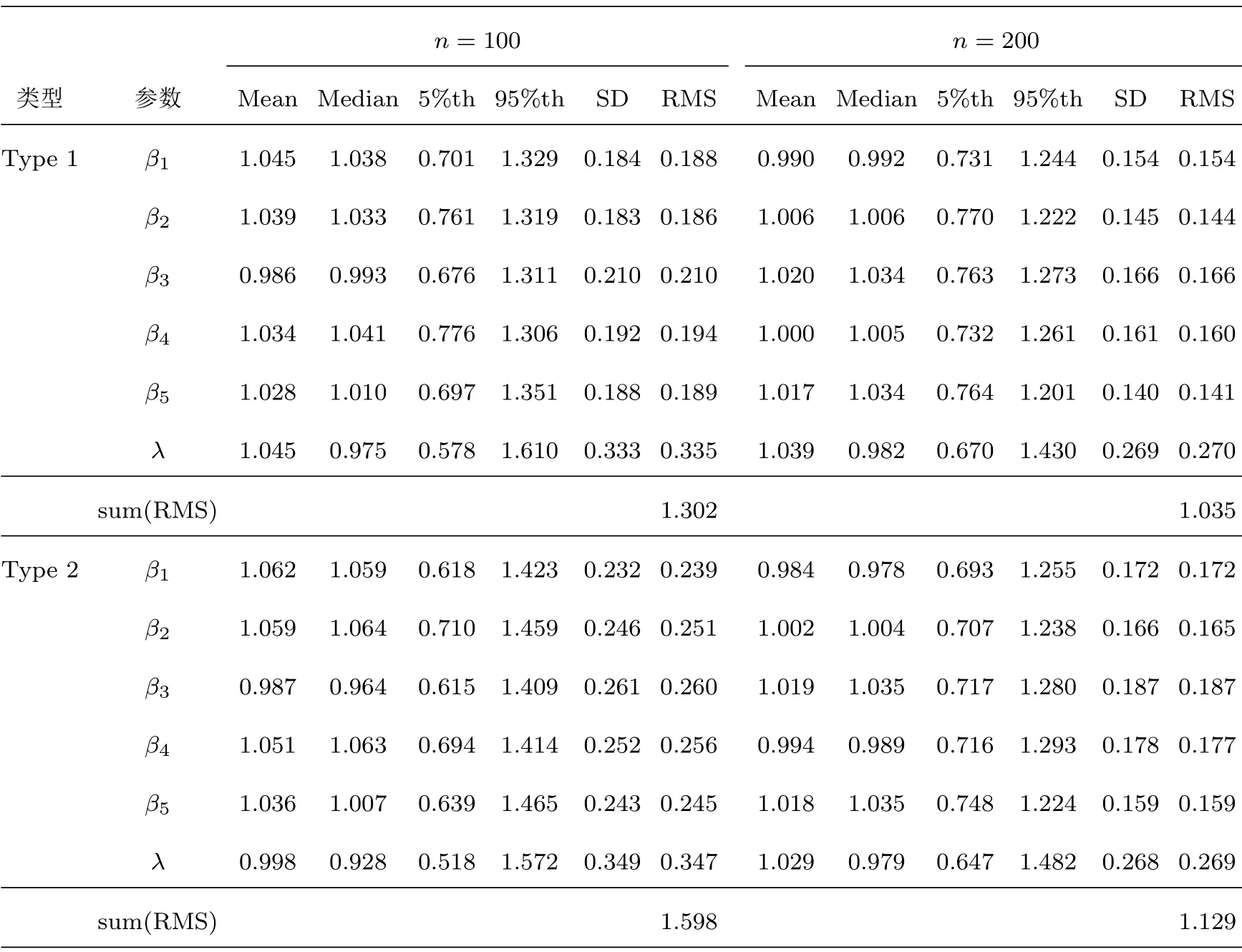
表1 模拟研究的数值结果(基于情形1)

实证分析的案例是1987-1988年美国医疗支出调查(the National Medical Expenditure Survey)数据.该数据的详细介绍和描述请参阅文[24].Gómez-Déinz等[25]曾经使用下列泊松高斯回归模型

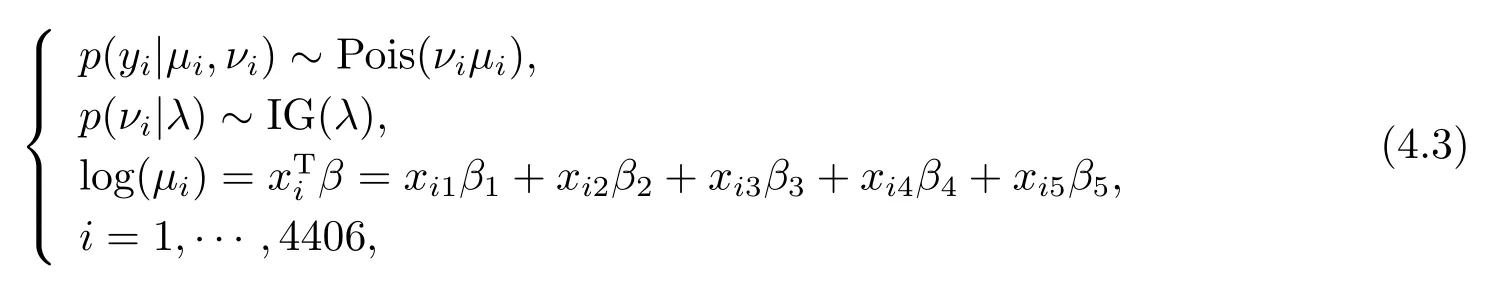
拟合该数据,其中响应变量yi= HOSPi,协变量xi1= 1,xi2= EXCLHLTHi,xi3=POORLHLTHi,xi4= PRIVINSi,xi5= MEDICAIDi,变量的具体含义由表3给出.相关参数的极大似然估计结果为= (−1.476,−0.950,0.878,0.138,0.264)T和= 0.139.在贝叶斯统计框架下,本文依然使用模型(4.3)拟合该数据并在参数的先验分布中选择如下的超参数:β0= (−1.476,−0.950,0.878,0.138,0.264)T,Hβ= 0.25I5和a=b= 1.在进行Gibbs抽样时,取σ2β= 3.6和σ2ν= 138,得到相应的β和ν的接受概率约为27.8%和32.5%.基于模型(4.3)和上述超参数设置,使用参数不同的初始值产生马尔科夫链计算参数的EPSR值[23].图1描绘了相应EPSR的计算结果.根据图1可知,当迭代次数iter numbers=500时,所有参数的EPSR值都未超过1.2.为了确保收敛,丢弃Gibbs抽样参数前1000次迭代的迭代样本,使用1000次迭代之后的3000个随机样本,按照(3.8)式计算模型未知参数的贝叶斯估计,表4是最终的估计结果.从表4可得,未知参数的贝叶斯估计为= (−1.537,−0.948,1.056,0.168,0.275)T和= 0.401.这和Gómez-Déniz等[25]的估计结果是基本相合的.另外,根据(3.11)式与(3.14)式并借助Gibbs抽

样收集的3000个随机样本计算拟合优度统计量,得到后验预测p值和偏后验预测p值的估计分别为= 0.513和= 0.595,结果一致表明所建立的模型(4.3)对美国医疗支出调查(the National Medical Expenditure Survey)数据的拟合效果比较理想.

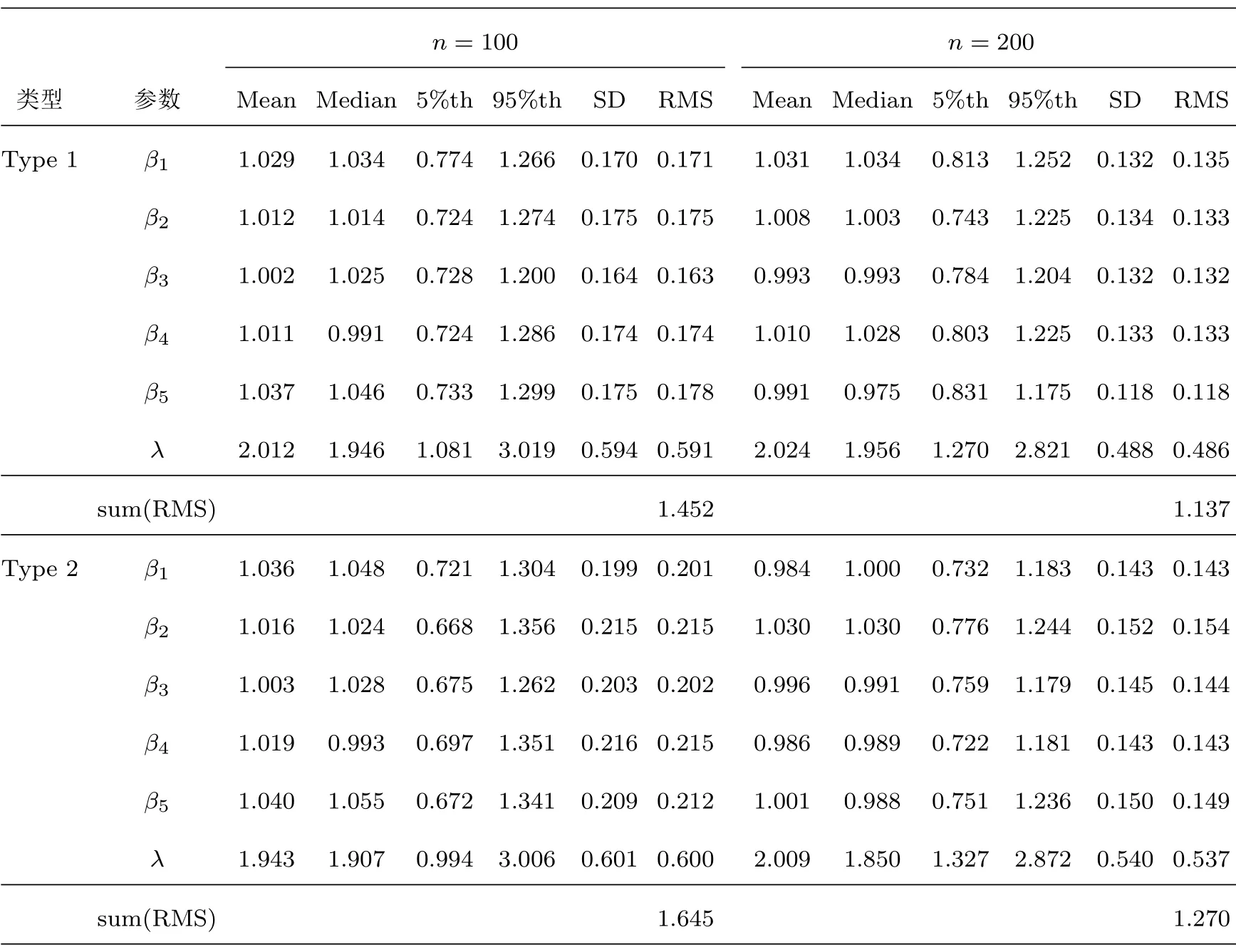
表2 模拟研究的数值结果(基于情形2)

表3 变量及其含义

图1 美国医疗支出调查数据分析所有未知参数的EPSR值

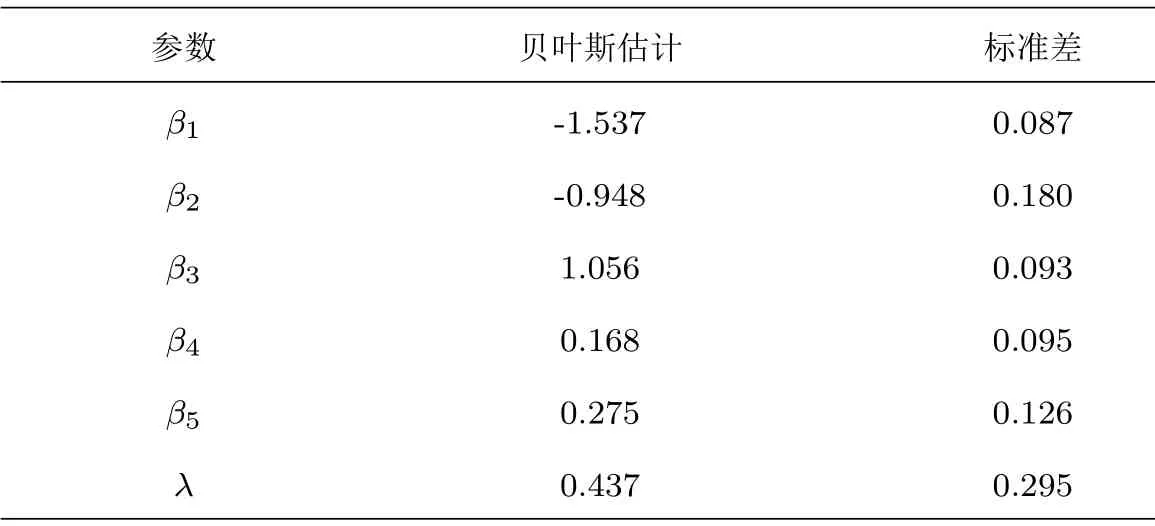
表4 美国医疗支出调查数据分析未知参数的贝叶斯估计

5.结论

文章在泊松逆高斯回归模型的框架下,借助Gibbs抽样与Metropolis-Hastings算法以及Multiple-Try Metropolis算法等MCMC方法进行贝叶斯统计推断研究.数值例子的结果表明,所描述的方法能有效地估计模型的未知参数和评价模型的拟合优度.

6.附录

根据3.2节的叙述,(3.6)式的分布是可以直接进行抽样的伽玛分布,但是(3.5)式与(3.7)式分布的抽样就十分棘手和困难.

对如何从(3.5)式的条件分布抽样β(t+1),本文采用Metropolis-Hastings算法[10-11].首先选取建议分布为N(0,σ2βΣβ),其中假设β在当前的迭代值为β(t),然后从N(β(t),σ2βΣβ)中随机产生潜在的转移样本β∗,并同时从均匀分布U(0,1)中独立地产生一个随机样本u,若则令β(t+1)=β∗,否则令β(t+1)=β(t).在具体使用MH算法时,经常选择σ2β使得β的接受概率位于区间[0.25,0.45].

Multiple-Try Metropolis算法[12]是一种重要的MCMC算法,被使用来对(3.7)式的条件分布p(νi|yi,xi,β,λ)进行抽样ν(t+1)i,其步骤为:1)从建议分布N(ν(t)i ,σ2ν)中独立地产生k个试验样本c1,c2,··· ,ck(比如k= 10,50等,本文取k= 10已足够);2)对任意j= 1,2,··· ,k,用式子πj=p(νi=cj|yi,xi,β,λ)计算πj,并做正则化处理,即令然后从试验样本c1,c2,··· ,ck中以概率p1,p2,··· ,pk随机挑选一个潜在转移样本ν∗,即从离散分布

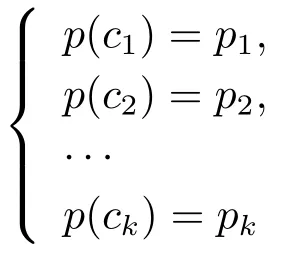
中随机产生一个样本ν∗;3)基于ν∗,从建议分布N(ν∗,σ2ν)中独立地产生k−1个参考样本c∗1,c∗2,··· ,c∗k−1,并令c∗k=ν(t)i.对任意j= 1,2,··· ,k,用式子π∗j=p(νi=c∗j|yi,xi,β,λ)计算π∗j;4)独立地从均匀分布U(0,1)中产生一个随机样本ε,若