Nonsingular Terminal Sliding Mode Control With Ultra-Local Model and Single Input Interval Type-2 Fuzzy Logic Control for Pitch Control of Wind Turbines
2021-04-16SaberAbrazehAhmadParvareshSaeidRezaMohseniMeisamJahanshahiZeitouniMeysamGheisarnejadandMohammadHassanKhoobanSeniorMemberIEEE
Saber Abrazeh, Ahmad Parvaresh, Saeid-Reza Mohseni, Meisam Jahanshahi Zeitouni, Meysam Gheisarnejad, and Mohammad Hassan Khooban, Senior Member, IEEE
Abstract—As wind energy is becoming one of the fastestgrowing renewable energy resources, controlling large-scale wind turbines remains a challenging task due to its system model nonlinearities and high external uncertainties. The main goal of the current work is to propose an intelligent control of the wind turbine system without the need for model identification. For this purpose, a novel model-independent nonsingular terminal slidingmode control (MINTSMC) using the basic principles of the ultralocal model (ULM) and combined with the single input interval type-2 fuzzy logic control (SIT2-FLC) is developed for non-linear wind turbine pitch angle control. In the suggested control framework, the MINTSMC scheme is designed to regulate the wind turbine speed rotor, and a sliding-mode (SM) observer is adopted to estimate the unknown phenomena of the ULM. The auxiliary SIT2-FLC is added in the model-independent control structure to improve the rotor speed regulation and compensate for the SM observation estimation error. Extensive examinations and comparative analyses were made using a real-time softwarein-the-loop (RT-SiL) based on the dSPACE 1202 board to appraise the efficiency and applicability of the suggested modelindependent scheme in a real-time testbed.
I. INTRODUCTION AND PRELIMINARIES
DUE to the shortage of fossil resources and the environmental issues resulting from greenhouse gas emissions, it seems necessary to pay more attention to renewable energy as an alternative energy source [1]. Wind energy has attracted much attention as an invaluable resource and one of the biggest potentials to meet the global energy demand [2]-[4]. Wind turbine technology, which operates under two configurations (i.e., constant and variable speeds)exploits the wind power to generate usable electrical energy for the customers. In the context of wind power production,the implementation of effective production equipment is necessary to optimize the conversion exploitation of such systems. The generation capacity of a wind turbine (WT)system is usually presented by a curve based on the form of power versus the wind velocity characteristics, as illustrated in Fig.1 [5]-[7]. In the first region, the wind speed is lower than the cut-in value and the turbine is not working. This working area is controlled to obtain the maximum power from the available wind. Region II is between the cut-in and the nominal speed power from the available wind, and its control objective is to capture the maximum available power from the wind flow using variable speed operation of the wind turbine.In region III, which is between nominal speeds and cut-out,the wind turbine system power curve remains constant at the rated power. And finally, the wind speed above the cut-out, or region IV, in which the turbine is powered down and stopped to avoid excessive operating loads.
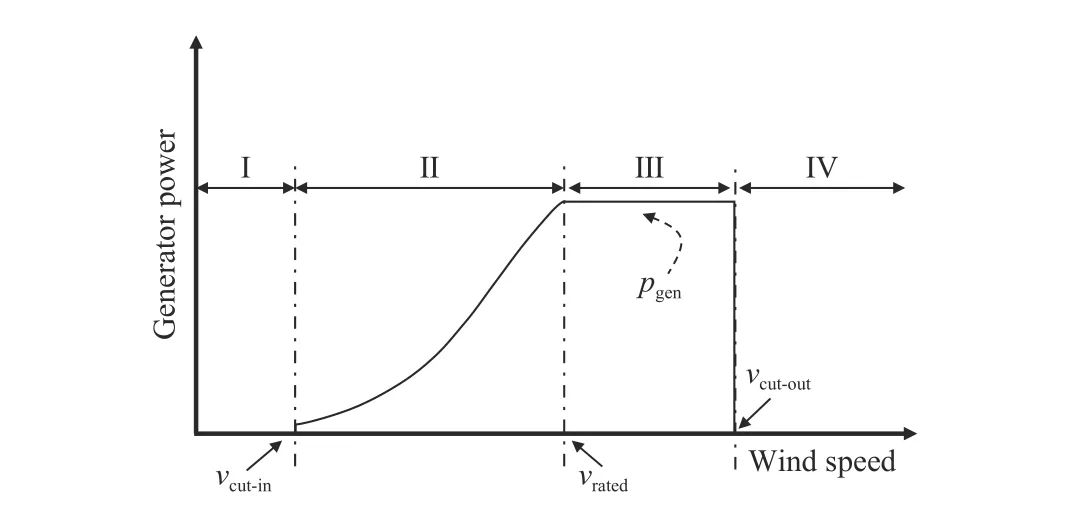
Fig.1. The operation modes of wind turbine.
The reliable and optimum operation of a wind power generation system depends on the control systems applied to the wind turbine operating in different regions. In region III,restrictions to the wind power are imposed by applying pitch angle control at the high speeds of this region [8]. Motivated by the real-world problems, developing a proper pitch angle control methodology, which is straightforward to design a wind turbine plant and also robust in terms of nonlinearities,becomes a significant challenge for the control society.Although, being everywhere in the industrial applications of the WT, the proportional integral derivative (PID) does not optimally perform, since necessary modifications such as extra notch filters are required in their structure to handle the nonlinearity of the wind power systems. To eliminate this problem, numerous robust controls such as backstepping controller [9], model predictive control [10], adaptive controller [11], interval type-2 fuzzy logic control (IT2-FLC)[12], and artificial neural network [13] were applied to design a robust scheme for the pitch angle controllers. For instance,aiming to design a controller with the disturbance rejection and reliable operation in the wind turbine systems, Muhando et al. [14] have proposed a pitch angle regulator-based gainscheduling scheme by minimizing the H∞-norm. Since the feedback gains in [14] are designed by the dynamic specifications, the suggested controller needs to be reconfigured against parametric uncertainty and faults. To overcome the deficiency of linear controllers in the wind turbine context, Boukhezzar and Siguerdidjane developed a nonlinear state feedback controller [15] which offers a right balance between optimal power exploitation and train load flexibility. They claimed that the suggested nonlinear scheme offers more efficient performance than the linear quadratic Gaussian, particularly for the extreme wind speeds.
The non-linear nature of the wind turbine aerodynamics necessitates adopting nonlinear controllers to regulate the power of the uncertain nonlinear plants, and to characterize the stability requirement. The sliding-mode control (SMC) is one of the most effective nonlinear controllers which has the ability to handle the nonlinear plants subjected to external disturbances [16]. To enhance the regulation capability of the standard SMC and improve some control specifications like finite-time stability, higher accuracy, and quick response,terminal SMC (TSMC) has been introduced [17]. To meliorate the convergence speed and overcome the problems associated with the singularity in the traditional TSMC scheme, a nonsingular version of the TSMC scheme, entitled NTSMC, is developed in [18], [19].
The developments of the model-based control schemes (e.g.,SMC [5], [16], H-infinity [20], fuzzy adaptive control [21],[22], adaptive neural network [23], [24], etc.) have been a topic of intense research in the wind turbine context in the literature. Although the model-based controllers might regulate the wind turbine power effectively, the mathematical model describing the plant dynamics needs to be developed.The main obstacle with these control methodologies is that the presence of un-modeled dynamics and parametric uncertainties in the wind turbine system are inevitable. In this situation these methodologies cannot produce satisfactory outcomes. In addition, a need for the full dynamic states of the system (as the feedback signal) makes the design of the model-based SMC controllers difficult as some turbine models require high-order controllers [25]. These difficulties provoked researchers to develop the model-independent controllers based on the intelligent PI (iPI) [26] and modelindependent SMC (MISMC) [27] for the indeterminate systems to offer a controller with less dependency on the plant dynamics and which compensates the variable parts of such systems.
Obtaining an accurate mathematical modeling of two-mass WT system is a challenging task due to the complexity of the mechanics, the chaotic and unpredictable conditions in which they work. The main objective of the current work is to design a model-independent controller (MINTSMC), for optimal capturing the power, that considers the nonlinear nature of wind turbines in the presence of unknown disturbances. Since the suggested controller is developed based on an ultra-local model (ULM) scheme, an observer-based sliding mode (SM)is designed for the estimation of the unknown phenomena(e.g., un-modeled dynamics, etc.). For the effective performance of the SM observer, it is essential that the unknown phenomena be bounded, otherwise, an estimation error appears when the observer coefficients are not properly set. To remove this estimation error, an auxiliary single input IT2 fuzzy PI (SIT2-FPI) [28] is added in this work to the observer-based model-independent control. The main contributions can be summarized as:
i) According to the knowledge of the wind turbine input and output measurements, an SM observer is designed to estimate the unknown dynamics.
ii) The pitch angle controller is designed based on the model-independent NTSMC scheme to eliminate the prevalent controller's complexity and enter the required control specifications.
iii) To compensate for the SM observer estimation error in order to ensure the finite-time convergence and ameliorate the system stability, an auxiliary SIT2-FPI is established in the suggested model-independent controller structure.
The rest of the work is organized as follows. The model of the studied wind turbine is given in Section II. The structure of the suggested model-independent controller is presented in Section III. Afterward, the real-time outcomes and comparison analysis are prepared in Section IV. In Section V,the conclusion and future scope are included.
II. WIND TURBINE NONLINEAR MODEL
The general scheme of a wind turbine with variable speed is illustrated in Fig.2, which comprises an aero turbine, mechanical components (gearbox and generator), and electrical devices (power electronic converter and grid connection).
As is well known, wind energy is first converted into mechanical energy through the wind turbine blades, and then into electrical energy through the generator, which is consequently transmitted into the power grid or consumed locally. For small analysis, a simplified representation of the 2-mass model of the wind turbine plant is presented in Fig.3[8], [15], [25].
The mechanical power extracted by the wind turbine is expressed by the following equation [15]:

Fig.2. Global scheme of wind turbines.
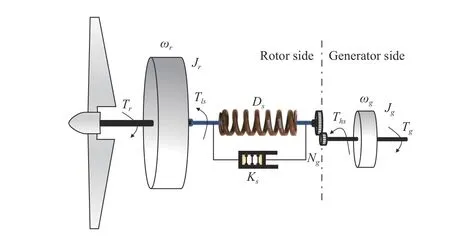
Fig.3. 2-mass dynamic model of aero turbine.
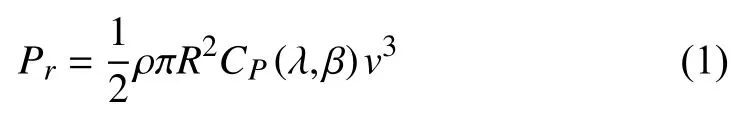
where ρ is the air density, R is the wind turbine rotor radius, v is the wind speed and CPis the power coefficient of the wind turbines which is a nonlinear function of the pitch angle β and tip-speed ratio λ. The parameter λ is calculated by the blade tip speed and wind speed upstream of the rotor as

with ωrbeing the rotor angular speed. The curves of CPwith respect to the multiple values of β are sketched in Fig.4.
The mechanical power Prcan also be rewritten as

where Tais the aerodynamic torque, given by

with Cq(λ,β) being the torque coefficient. Furthermore, it can be readily obtained that

Cq(λ,β) is generally determined experimentally and provided by the manufacturers [29]. In practice, an acceptable numerical approximation can be adopted.

where

The nonlinear wind turbine model is shown in a generalized nonlinear form as follows [8]:

The state vector x, control input uand nonlinear vector G(x)are defined as
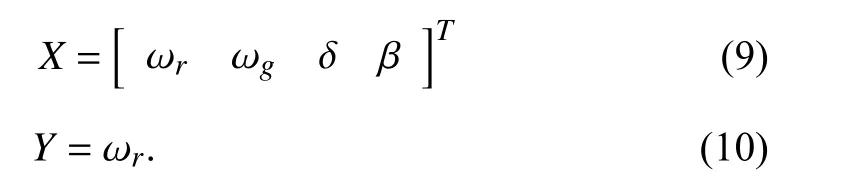
These parameters are listed in Table I.

TABLE I PARAMETERS OF THE 1.5 MW EXPERIMENTAL WIND TURBINE
The current work aims to develop a novel modelindependent pitch angle controller for rotor speed regulation at region III of the wind turbine operation by restricting the power derived from the wind turbine.
In the next sub-section, the overall structure of the suggested model-independent control scheme and the procedure for designing the controller gains are presented.
III. DESIGN OF MODEL-INDEPENDENT NTSMC BASED IT2-FLC
Based on the fundamental concept of the ULM control scheme, a combination of SIT2-FPI and model-independent NTSMC scheme is introduced which includes three subcontrollers: i) Firstly, an NTSMC controller is adopted in the model-independent framework to reduce the dependency of the existing controller to the wind turbine model and handle the plant’s nonlinearity; ii) Then, an SM observer is designed to estimate and eliminate the time-varying disturbances and un-modeled terms; iii) And additionally, an auxiliary controller-based SIT2-FPI structure is incorporated into the ULM to compensate the estimation error of SM observer and to enhance the overall transient behavior.
A. Model-Independent NTSMC Technique
Definition 1: For a general nonlinear plant, the modelindependent control that is described in [26], [30] and the ULM form which is approximately defined by (11) can be adopted to express the system dynamics.
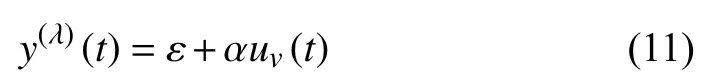
where y (t) is the output term, v is the derivative order, ε is the unknown structure of the plant as well as any disturbances which are estimated based on the input signal u(t) and output y(t) , α ∈R is an assumed constant.
Definition 2: To determine the sliding surface, the new state variables x1and x2are introduced as
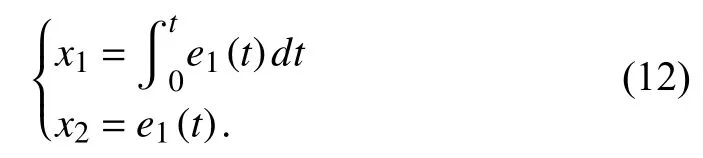
According to (12), the state-space equations are given as

Based on the SMC framework, a second-order NTSM is presented in (14) with the designed parameter γ , and the p and q are odd defined as1 <p/q <2.

By differentiating (14), one can obtain

Theorem 1 [27]: For the state-space equation given in (12),if the NTSMC manifold is considered as (14) and control law is formulated as (16), then one has e →0 in finite time.
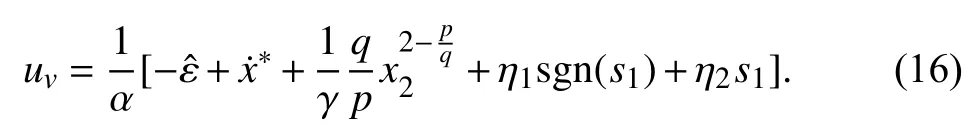
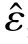
Proof: The Lyapunov function, as usual, is chosen as

If (17) is differentiated with respect to time, and (15) is substituted into it, one can obtain



when η1>‖ε‖+μ(μ >0), (19) will be transformed into the following inequality:

Thus, the stability of the controller will be satisfied by the demand of the Lyapunov theory. ■
B. Design of SM Observer

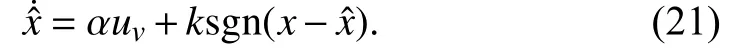

Definition 3: Let us define the observer error as

In the next step, by subtracting relation (11) from (22), the dynamic error equation can be obtained, given as


Proof: Let us define the Lyapunov function as

If (24) is differentiated with respect to time, the following equation is attained:

Selecting k by k >‖ε‖+η(η >0) yields

The structure of the established model-independent scheme,which comprises the MINTSM controller with SM observer,is illustrated in Fig.5 [27].
C. Auxiliary Controller-Based SIT2-FLC Structure

Fig.5. Block diagram of MINTSMC scheme with SM observer.
In this sub-section, the performance output of the MINTSMC controller is improved by adding an extra control signal to the system to reduce the observer estimation error.The auxiliary controller which is exploited in this paper, the SIT2-FPI controller, is depicted in Fig.6. In this diagram, kpand kiare the coefficients of the baseline PI controller and kedenotes the input scaling factor (SF). Based on the given scheme, the SIT2-FPI control signal uSIT2is utilized by the output action of the controller (φo) that is shown in (27) [32], [33].




where χ denotes the learning rate; c1and c2denote acceleration coefficients; R1and R2indicate random numbers within [0 1]. The bounds of the model-independent controller coefficients , , , , are chosen to be 0 and 200.
Remark 1: In the following, the advantages of the suggested model-independent scheme are summarized.
i) In comparison with the model-based control strategies(model predictive control, backstepping controllers), the suggested scheme is developed based on the measured input/output (I/O) data of the system which remove the need to model identification,
ii) In compassion with the conventional SMC and TSMC approaches, the quick time convergence and the elimination of singularity problems are achieved by the NTSMC.
iii) In compassion with the MINTSMC approach with SM observer, an auxiliary controller-based SIT2-FLC is established in the MINTSMC structure which removes the observer error and ameliorates the pitch angle performance of the WT plant.
iv) In comparison with the conventional type-1 and interval type-2 FLCs with two inputs [22], [38]-[41], the SIT2-FLC controller does not need to adjust the rule base and membership functions which is valuable in practical applications.
Ξ={γ η1η2kpki}
IV. EXPERIMENTAL RESULTS
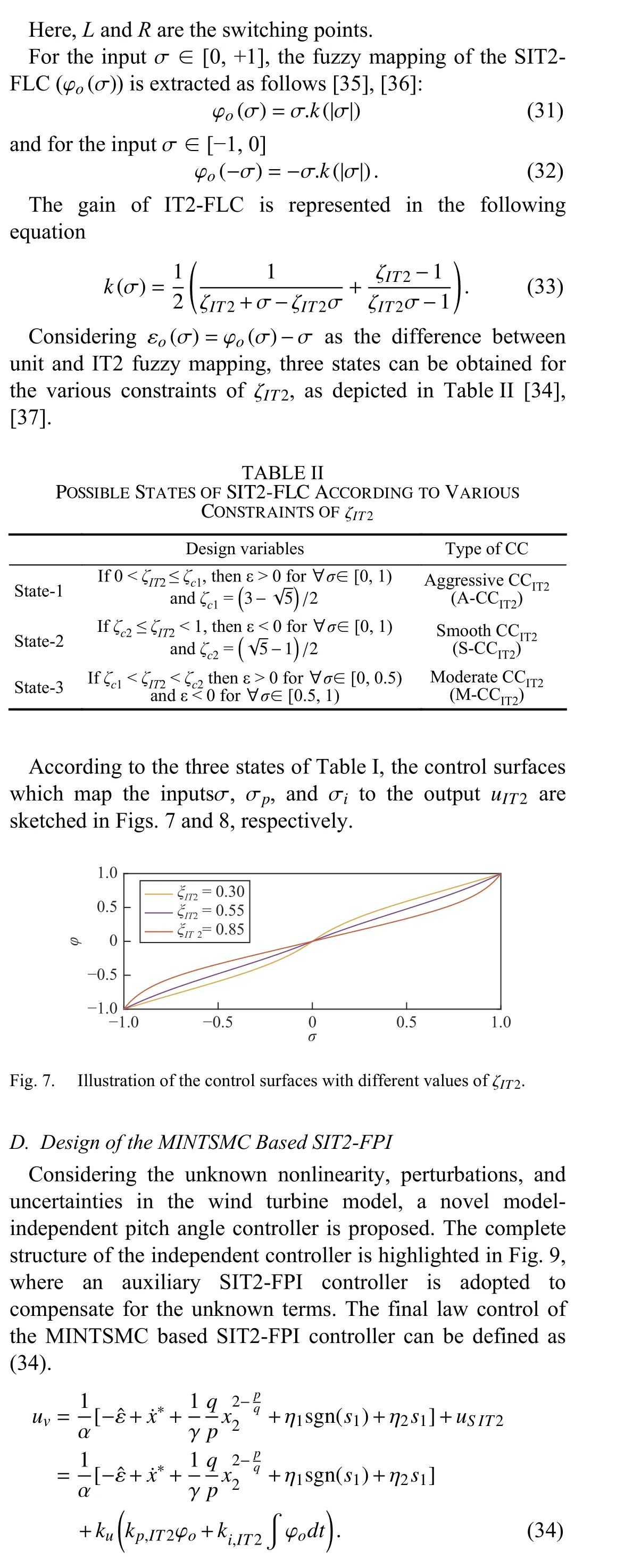
The essence of designing ULM control based on the modelindependent scheme is to offer optimal performance for the wind turbine plant under the various level of wind speed variations without the need for model identification. The suggested model-independent scheme was examined by the wind turbine modeled as a 2-mass model using a real-time software-in-the-loop (RT-SiL) simulation. The SiL platform integrates the compiled source code into a functional model simulation to offer a virtual simulation environment for the examination of the control methodologies for complex problems. In comparison with the traditional off-line simulations, the SiL platform provides a real-time simulation to modulate some delays and small errors as well as the effect of the computational burden on the transient performance. The necessary steps for the realization of the SiL setup based on the dSPACE 1202 board are illustrated in Fig.10. In this application, the model of the test system along with the control strategy was run in real-time using the Runge Kutta’s solver with a sampling frequency of 10 kHz [1]. The parameters of the 2-mass WT model in this work are considered from [8].
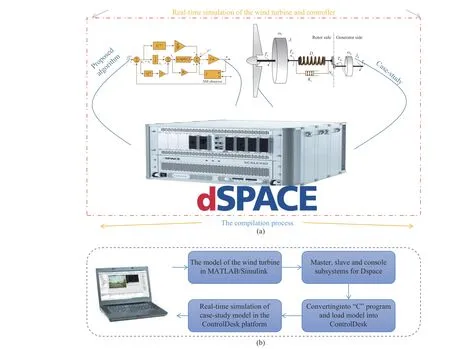
Fig.10. Steps for executing RT-SiL setup.
The transient outcomes of the MINTSMC based SIT2-FPI controller are verified under four typical scenarios of the wind turbine, as i) the step changes of the wind, ii) the random fluctuation of the wind speed iii) parametric uncertainty in the turbine model, and iv) simultaneous change in wind speed and system parameters. Since region III is selected as the operation region of the pitch control, the wind speed for the tested scenarios is considered in the range of [12 m/s 14 m/s].In the comparative studies of the real-time setup, the transient outcomes of the suggested model-independent controller are compared with those of MINTSMC, N-PI [8], and PI [8]controllers.
Initially, the dynamic performance of the suggested modelindependent controlled wind turbine is investigated by applying the multi-step wind speed variation shown in Fig.11.The optimization issue with the number of particles Np= 50 was solved for the MINTSMC based A-SIT2-FPI (with setting ζIT2= 0.30), the MINTSMC based M-SIT2-FPI (with setting ζIT20.55) and the MINTSMC based S-SIT2-FPID (with setting ζIT2= 0.85). The convergence specifications of the best-explored solutions for the three SIT2-FPI modes over 30 iterations are illustrated in Fig.12. It is seen that the convergence of F(t) under the A-SIT2-FPI action is recognized to be best among the three compared SIT2-FPI controllers.

Fig.11. Multi-step variation of wind speed.
Scenario 1 (Dynamic Performance With the Step Wind Speed): The SiL responses for the MINTSMC based SIT2-FPI, MINTSMC, N-PI, and PI controllers under the multi-step speed disturbance of Fig.11, which comprises the outcomes of rotor speed, shaft twist angle, pitch angle and mechanical power are presented in Figs. 13(a), 13(b), 13(c), and 13(d),respectively.
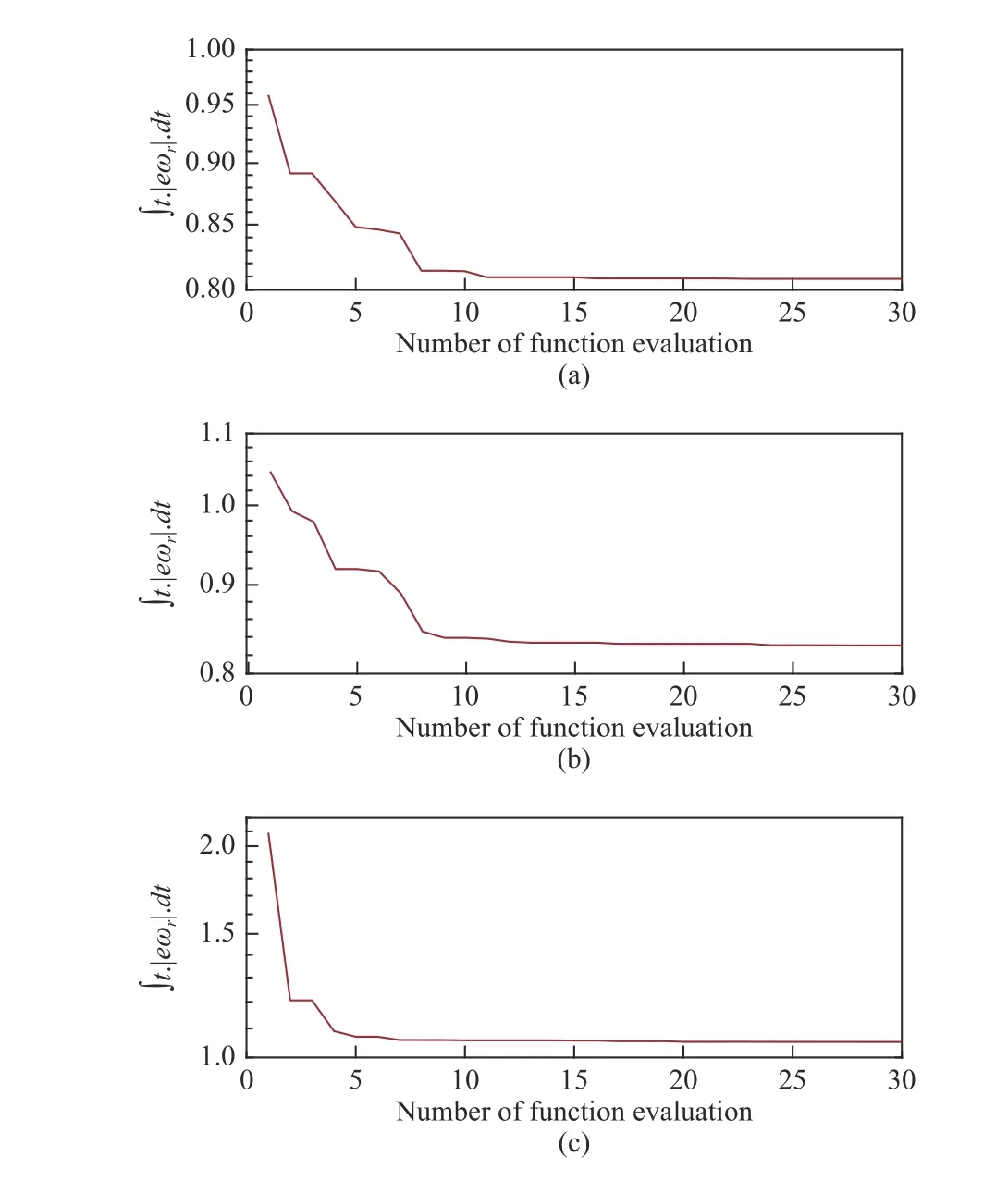
Fig.12. Convergence specifications of MINTSMC based SIT2-FPI with(a) A-CC IT2, (b) M-CC IT2, (c) S-CC IT2.
The real-time outcomes reveal that the N-PI and PI controllers experience large overshoot with undamped oscillations. Also, it is seen that, in spite of the MINTSMC approach which exhibits acceptable robust behavior, there remains a non-zero steady-state error in the test system outcomes. In contrast, the dynamic outcomes reveal that with the suggested controller (realized based on the SIT2-FPI), the system outcomes are alleviated with small deviations in a shorter time and better satisfy the steady-state requirements than the other three controllers.
Scenario 2 (Dynamic Performance With the Wind Speed Fluctuation): To validate the feasibility of the suggested model-independent scheme against the real-world wind, a random fluctuation of wind speed is applied to the concerned 2-mass model wind turbine, and its corresponding profile is sketched in Fig.14(a). The comparative rotor speed outcomes of the four-pitch angle controllers under the real wind speed data are illustrated in Fig.14(b).
From Fig.14(b), it is seen that the N-PI and PI controllers undergo undesirable overshoot and large settling time.Moreover, the MINTSMC requires a relatively long regulation time to derive the speed rotor deviation to its reference value,while with adding the auxiliary SIT2-FPI controller, superior outcomes are offered by eliminating the SM observer estimation error and improving the steady-state requirements.
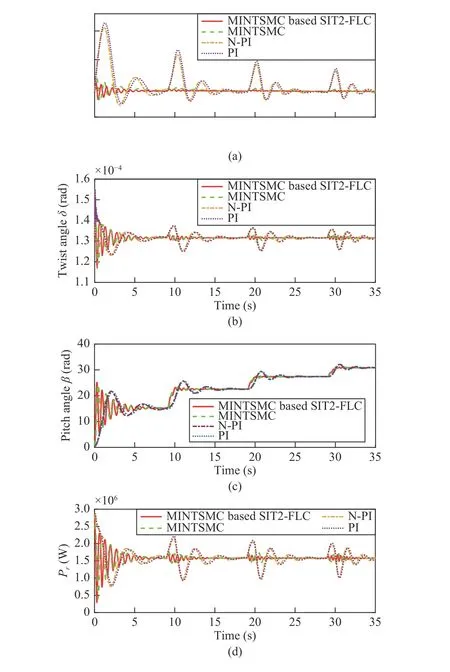
Fig.13. Time-domain behavior comparison of the suggested scheme,MINTSMC, N-PI, and PI according to multi-step wind test. (a) rotor speed,(b) twist angle, (c) pitch angle, (d) mechanical power.
Scenario 3 (Robustness Against Parametric Uncertainty):In order to examine the influence of the parametric uncertainties, some parameters of the WT are changed as: Rb= +25%, Jr= +50 % and tβ= +75% . The corresponding two standard error measurement criteria including mean square error (MSE) and root MSE (RMSE) after applying the variations to the test system are reported in Table III. Looking at the performance indices presented in Table III, one can observe that with the suggested controller, the calculated values of the error measurement indices in all the test validation cases are best, consequently, superior robustness is reached while comparing with the others. Results of the rotor speed corresponding to the large positive parametric uncertainties for the various designed pitch angle controllers are illustrated in Fig.15(a)-(d).
Remark 2: From the outcomes of the four scenarios, it is explored that with the application of PI and N-PI controllers,the responses of the WT system experience a large deviation.Moreover, despite the MINTSMC approach that can stabilize the outcomes of studied 2-mass WT plants, the system responses are not optimal under the wind speed changes and system uncertainties. However, with the suggested MINTSMC based SIT-FLC controller, the system outcomes are further alleviated than other designed pitch angle controllers.
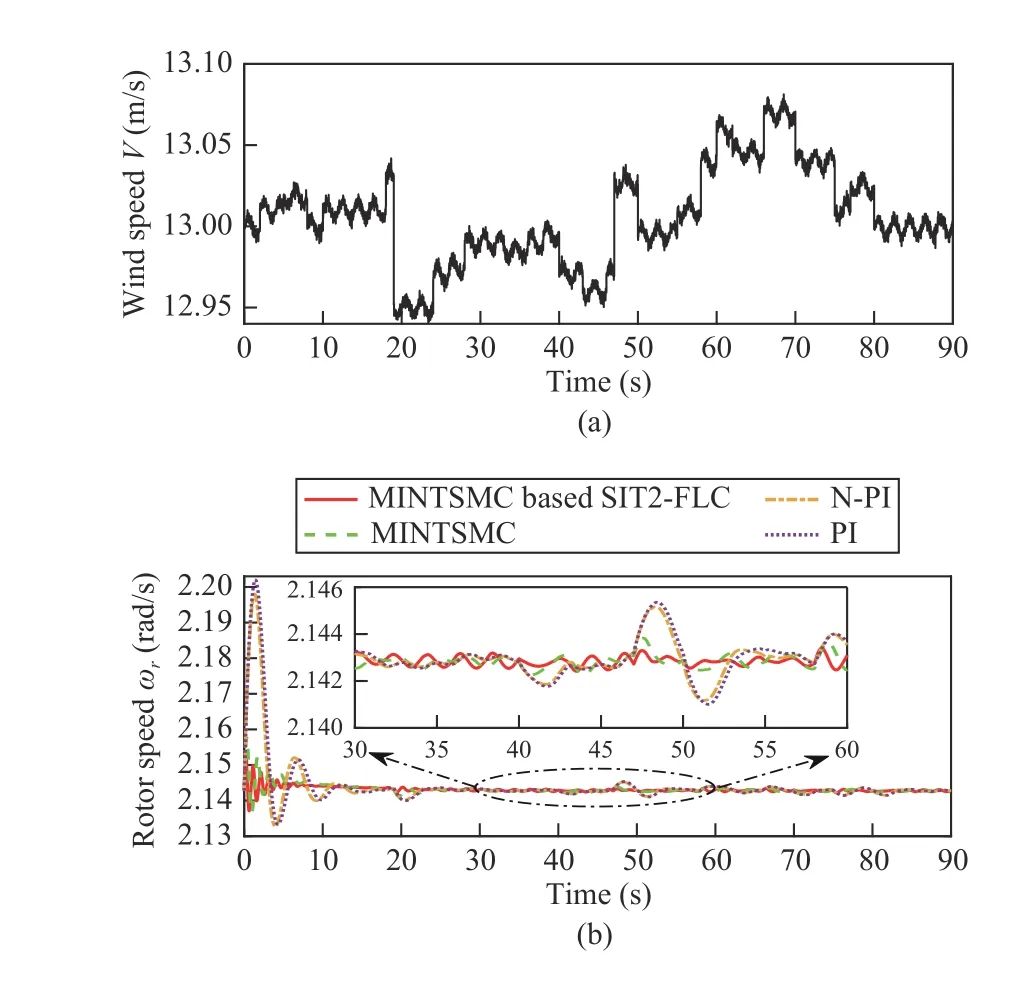
Fig.14. The time-domain response of suggested scheme, MINTSMC, N-PI,and PI according to random fluctuations of wind (a) random wind speed,(b) rotor speed.

TABLE III COMPASSION OF MSE AND RMSE STANDARDS FOR THE PARAMETRIC UNCERTAINTIES
Scenario 4 (Robustness Against Wind Speed Changes and Perturbed Condition of Air Density): Additionally, to ascertain the robustness of the suggested model-independent scheme in a more severe condition, the effect of the change in wind speed and uncertainty in the air density are tested simultaneously. Absolute maximum wind speed deviation when the wind speed is changed from 12 m/s to 24 m/s, and the value of ρ is changed from nominal condition to +50%(i.e., it is changed from 1.2250 kg/m3to 1.8375 kg/m3), is shown in Fig.16.
V. CONCLUSION
The present work concentrates on developing a combination of MINTSMC and SIT2-FPI controllers for pitch control of a wind turbine plant. The main outcomes of this research project are:

Fig.15. Time-domain outcomes according to uncertain parameters (a) suggested scheme, (b) MINTSMC, (c) N-PI, (d) PI.
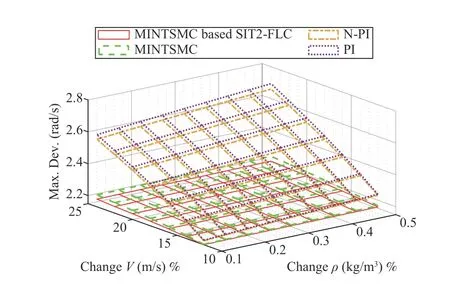
Fig.16. Absolute maximum wind speed deviation against wind speed change.
i) An auxiliary SIT2-FL is incorporated into the ULM control scheme to ameliorate the overall performance of an existing MINTSMC controller and eliminate the SM observer estimation error.
ii) The performance of the designed pitch angle controller in tracking the wind speed rotor under both cases of multi-step and fluctuation wind disturbances is verified.
iii) The comprehensive tests based on the SiL platform are conducted on a simplified 2-mass model of a wind turbine to validate the applicability of the model-independent controller from the real-time perspective.
iv) Simultaneous consideration of the wind speed change and uncertainty in the air density of the nonlinear system can be regarded as another outcome of this research.
Since the chattering adversely affects the system performance which deteriorates the system performance and imposes instabilities; as future work, the chattering attenuation NTSMC can be developed to eliminate this phenomenon. For this purpose, the switching function in the SMC controller should be designed in such a way that mitigates the effect of chattering over time.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Ground-0 Axioms vs. First Principles and Second Law: From the Geometry of Light and Logic of Photon to Mind-Light-Matter Unity-AI&QI
- Deep Learning for EMG-based Human-Machine Interaction: A Review
- Distributed Secondary Control of AC Microgrids With External Disturbances and Directed Communication Topologies: A Full-Order Sliding-Mode Approach
- Deep Learning in Sheet Metal Bending With a Novel Theory-Guided Deep Neural Network
- Autonomous Control Strategy of a Swarm System Under Attack Based on Projected View and Light Transmittance
- Computing Paradigms in Emerging Vehicular Environments: A Review
