Autonomous Control Strategy of a Swarm System Under Attack Based on Projected View and Light Transmittance

Xuejing Lan, Wenbiao Xu, Zhijia Zhao, Member, IEEE, and Guiyun Liu

Abstract—In the study of a visual projection field with swarm movements, an autonomous control strategy is presented in this paper for a swarm system under attack. To ensure a fast swarm dynamic response and stable spatial cohesion in a complex environment, a new hybrid swarm motion model is proposed by introducing global visual projection information to a traditional local interaction mechanism. In the face of attackers, individuals move towards the largest free space according to the projected view of the environment, rather than directly in the opposite direction of the attacker. Moreover, swarm individuals can certainly regroup without dispersion after the attacker leaves. On the other hand, the light transmittance of each individual is defined based on global visual projection information to represent its spatial freedom and relative position in the swarm. Then, an autonomous control strategy with adaptive parameters is proposed according to light transmittance to guide the movement of swarm individuals. The simulation results demonstrate in detail how individuals can avoid attackers safely and reconstruct ordered states of swarm motion.

I. INTRODUCTION

SWARM movement is the collective behavior form of a large number of individuals with a common goal, which widely exists in animals such as birds, fishes, insects and mammals [1]-[4]. It is believed that swarm movement can raise collective awareness and provide protection from predators [5], [6]. Through individual decision-making, these biological swarms eventually show self-organization,cooperation, stability and adaptability to the environment [7],[8]. These characteristics of swarm movement are closely related to the requirements of locality, distribution and robustness in the coordinated control of many practical application scenarios, such as multi-aircraft surveillance,multi-robot cooperative search, and multi-missile saturation attacks [9]-[12]. For example, in a typical military attack mission with a known target location, swarm missiles need to cooperate to attack the target and avoid the attack of a defender at the same time. The study of a swarm motion model provides a feasible way to solve practical coordination and autonomous control problems [13]-[15]. Therefore, in recent years, internal causes of determining how to coordinate the process of swarm motion have been investigated by relevant researchers.

According to the observations of real bird populations, it has been determined that a bird only responds to the position and orientation of its seven nearest neighbors. Therefore, most current swarm models assume that information is exchanged among neighboring individuals for cooperative movement.Reynolds [16] first proposed the Boid model, in which individuals perceive the local information of the dynamic environment within a certain range, and perform the three principles of collision avoidance, velocity matching and flock centering. On this basis, the Vicsek model, Couzin model,Cucker-Smale model, inertial spin model, etc. appeared one after anothers [17]-[21]. The Olfati-Saber model implements the three principles of Boid model by introducing artificial potential fields. To complete swarm motion under different dimensions and different obstacles, three different types of agents are defined: agents that follow the three principles of movement, agents with known moving targets, and virtual agents that are near obstacles [22]. Lan et al. [23], [24]introduced the idea of adaptive dynamic programming and reinforcement learning into the swarm motion model, which can adapt to the unknown obstacle environment intelligently.In addition, Cheah et al. [25] proposed a dynamic regionbased swarm motion model by restricting all agents to a certain geometric regions. Then, Lan et al. [26] extended the region-based swarm motion model to solve the problems of member loss, narrow space, and group merging. With this model, geometric regions could not only expand or contract,but also change shape to adapt to the changing environment.

The current motion models of large-scale swarm systems mainly involve the three basic principles of the Boid model or simply, the region shape to guide the swarm behavior. Local interaction is sufficient to establish order in a swarm, but does not provide any information about the state of the entire swarm. We believe that the local interaction among neighboring individuals alone is not sufficient to explain the organization of large groups of swarms [27]-[30]; thus, it is necessary to study new swarm behavior mechanisms to meet the needs with the rapid interaction of global information in complex environments. Here, the key is determining a method to construct telematic mechanisms among individuals in the swarm. Recently, Cavagna et al. [31] constructed a new swarm motion model, where the individual is regarded as the liquid component in a fluid field. Thus, the density wave generated by a change of individual position and a spin wave generated by the change of individual direction can provide the role of information interaction. On the other hand, the study of the visual projection field in swarm movements is very popular with scholars [32]-[35], and some swarm motion models are proposed based on vision information [36]-[38].Pearce et al. [33] put forward a new view on the cause of bounded swarms: individuals in a swarm maintain the opacity of a swarm by responding to visual projection information formed by dark birds and the bright sky behind them. The projected view of the environment observed by individuals can be applied as a global interaction mechanism to provide fast information interaction and a swarm dynamic response,which has great advantages over the traditional local interaction model. Moreover, Bastien and Romanczuk [39]proposed a purely vision-based model to realize the collective behavior for autonomous swarm robotic systems.

In order to meet the needs of rapid interaction of global information in a complex environment, and to maintain an ordered swarm motion without dispersion at the same time, a new hybrid swarm motion model is proposed in this paper by introducing the projected-view-based global interaction mechanism. Two cooperative behavioral modes switch according to their current perception to ensure the security of a swarm and the completion of a given task. Then an autonomous control strategy is provided to guide the movement of swarm individuals. Compared with existing swarm research results, the main contributions of this paper are as follows:

1) A hybrid swarm motion model is proposed by combining a projected-view-based global interaction mechanism and a traditional local interaction mechanism.

2) The light transmittance of each individual is defined based on the projected view to represent its spatial freedom and relative position in the swarm.

3) An autonomous control strategy with adaptive parameters is proposed according to the light transmittance to guide the movement of swarm individuals under attack.

The rest of this paper is arranged as follows. The dynamics of the individual and the projected view are described in Section II. The projected-view-based hybrid swarm model is presented in Section III with behaviors of cohesive,separation, alignment, attacker avoidance, and task execution.Section IV discusses the autonomous control strategy with adaptive parameters. A simulation is given in Section V to show the effect of autonomous control strategy. Finally,Section VI comes to a conclusion.

II. BACKGROUND STATEMENT

III. PROJECTED-VIEW-BASED HYBRID SWARM MODEL

In this section, we present a hybrid swarm motion model in which each individual responds to the projected view of the environment it observes. Instead of the attraction component of the traditional local interaction model, global visual projection information is used to model the cohesive behavior and attacker avoidance behavior of the swarm to provide fast information transmission and swarm dynamic response. The local interaction of separation and alignment is included in the hybrid swarm motion model to maintain an orderly organization of the swarm. In addition, the task execution behavior of the swarm is also considered to ensure the completion of a given task.

A. Cohesive Behavior

The movement of each individual always tends to move closer to other individuals to keep safe. In order to meet the needs of the rapid interaction of global information in a complex environment, the projected view caused by other individuals is used to model the cohesive behavior. Therefore,the characteristic direction of cohesive behavior for an individual i can be produced by

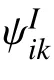
B. Separation Behavior

At the same time, it is impossible for individuals to approach each other infinitely, as this will cause collisions.Therefore, when the distance between the individuals is too close, the individual will move in the direction of escaping the opponent one. The position error vector between the individual i and individual j is defined as pij=pi－pj. Then,the characteristic direction of the separation behavior can be produced by

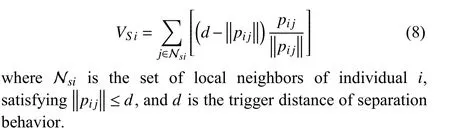
C. Alignment Behavior

Individuals tend to align with their visible several local neighbors to maintain orderly organization of the swarm [40].Visible local neighbors are defined as having an unbroken line of sight between the two individuals. It is assumed that only four nearest visible local neighbors are chosen by an individual to follow. Therefore, the characteristic direction of the alignment behavior can be produced by

D. Attacker Avoidance Behavior

Because the attackers (obstacles, predators) are uncontrolled, it is not feasible to adopt the same strategy for avoiding collisions between individuals. If an individual moves directly in the right opposite direction of the attacker once it senses the attacker (within its detection range), the individual will encounter other individuals in the swarm,which will lead to deadlock or even collision (especially the need to escape attackers faster). Therefore, the strategy should enable the individual to keep away from the attackers, but not turn back directly into the dense swarm. Thus, it seems to be a good idea for individuals to move towards free space. Then,the projected view caused by other individuals and attackers can be used to model attacker avoidance behavior.

The union of all effective free space of individual i can be expressed as a complement of the projected view caused by other individuals and attackers.

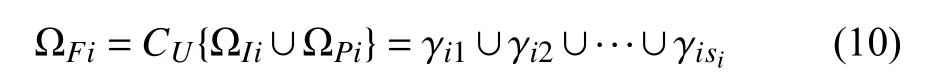
where U=[0, 2π). γik=ξik－Δξik, ξik+Δξikis the continuous free space of individual i. The index k ∈[1,si] spans all silight fields seen by the it h individual. γik∩γiq=Ø , k ≠q.The polar angle ξikis the direction of light field γik, and Δξikrepresents half of its angular range.

Therefore, the characteristic direction of attacker avoidance behavior can be produced by

E. Task Execution Behavior

In addition, we should also consider the task execution of the swarm, such as tracking a fixed or moving target (catching food, attacking) and migrating to a destination. Therefore, the characteristic direction of the task execution behavior can be produced by

where pt∈R2is the position of the target or destination known by the individuals.

IV. AUTONOMOUS CONTROL STRATEGY

By observing the movement of jackdaws, it is concluded that there are two interaction modes: one is topological interaction with a fixed number of neighbors when flying to roosts, and the other is metric interaction according to spatial distance when encountering predators [3]. Inspired by this phenomenon, an autonomous control strategy is proposed with two cooperative behavioral modes. One behavioral mode is implemented to ensure the security of swarm, and the other is to ensure the completion of a given task. The two behavioral modes switch according to the current situation of the individual. The security-based behavioral mode has a higher priority than the task-based behavioral mode. When an individual perceives an attacker or an impending collision with another individual, it executes the security-based behavioral mode. Otherwise, the task-based behavioral mode is executed only when an individual is in a safe state. Then, to realize the desired behavioral mode, a control law is designed to track the given reference velocity.

A. Security-Based Behavioral Mode

In the security-based behavioral mode, an individual tends to avoid collisions with the other individuals and prefers to keep away from attackers. Thus, the reference velocity of individual i is designed as

where an arrow (⇀) on the variable indicates that the vector is normalized. VSiand VFiare determined by (8) and (11),respectively. The parameters λsand λfare the adaptive weights of the collision and attacker avoidance behaviors,respectively. It is known that the light transmittance of each individual can represent its spatial freedom and relative position in the swarm roughly. The higher the light transmittance is, the larger the space for individuals to avoid collision and attackers quickly is. Thus, λs=gs(Θi) and λf=gf(Θi) are designed to be increasing functions of light transmittance.

B. Task-Based Behavioral Mode

In the task-based control strategy, individuals tend to execute tasks while maintaining the orderly organization of the swarm, such as tracking a fixed or moving target (catching food, attacking) and migrating to a destination. Thus, the reference velocity of individual i is designed as

where an arrow (⇀) on the variable indicates that the vector is normalized. VCi, VAiand VTiare determined by (7), (9) and(12), respectively. The parameters λc, λaand λtare the adaptive weights of the cohesive, alignment and task execution behaviors, respectively. With swarm movement, it is very dangerous for individuals to leave the swarm.Therefore, compared with task execution behavior, those individuals at the edge of the swarm are required to give priority to the cohesive and alignment behaviors. It is known that the light transmittance of individuals at the edge of a swarm is generally higher than that of the individuals in the center of a swarm. The higher the light transmittance is, the closer the individual is to the edge of the cluster. Thus,λc=gc(Θi) and λa=ga(Θi) are designed to be increasing functions of light transmittance. Meanwhile, λt=gt(Θi) is designed to be decreasing functions of light transmittance.

C. Control Law

The behavioral mode of individuals determines their reference velocity. The purpose of designing a control law is to enable individuals to move at the desired velocity. In this paper, a simple proportional controller is designed for an individual i to track the given reference velocity as follows:

where kvis the proportion coefficient of the control law and influences the magnitude of the control input. The larger the parameter kvis, the larger the control input is. Viris the reference velocity of individual i determined by (13) or (14),depending on the current behavioral mode of the individual.The parameters λs, λf, λc, λaand λtdetermine the relative proportion of the corresponding behavior in the reference velocity, and further influence the direction of the control input. The larger the parameter is, the closer the reference velocity is to the characteristic direction of the corresponding behavior.

Fig.2. The detail positions of individuals, attackers and destination at different times. (The small colored dots represent the individuals, the big black dots represent the attackers, and the red triangle represents the destination. The arrows on individuals and attackers represent their current velocity vectors. The number attached to the upper right corner of each individual represents its current light transmittance).

V. SIMULATIONS

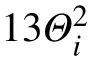
The detail positions and velocities of individuals, attackers and destination are shown in Fig.2, at t=0 s, t=9 s, t=12 s,t=15 s, t=18 s, t=21 s, t=24 s, t=27 s, t=34 s, t=39 s,t=43 s, and t =52 s, respectively. The small colored dots represent the individuals, the big black dots represent the attackers, and the red triangle represents the destination. The arrows on individuals and attackers represent their current velocity vectors. The number attached to the upper right corner of each individual represents its current light transmittance. The distribution of light transmittance can roughly show the spatial freedom of each individual. It can be seen that the light transmittance of individuals at the edge of a swarm is generally higher than that of the individuals in the center of a swarm. The higher the light transmittance is, the closer the individual is to the edge of the cluster. Fig.2(a)shows the initial positions of individuals. In Fig.2(b), one individual firstly perceives the attacker and begins to run away from the attacker. Then, the results of some representative moments in the process of attacker avoidance of individuals are illustrated in Figs. 2(c)-2(k), which show in detail how individuals can avoid the attackers safely and effectively when encountering attackers. The simulation ends at t=52 s with the result shown in Fig.2(l), where one of the individuals is within 1 m of the destination.

Taking the swarm state at t=21 s as an example, the reference velocities of individuals in different behavioral modes are given in detail in Fig.3. The small colored dots with an indexing number attached in the upper right corner represent the swarm individuals. The big black dots represent the attackers. The green arrows represent the reference velocities of individuals in the task-based behavioral mode directly,which is composed of cohesive, alignment and task execution behaviors. The red arrows represent the reference velocity components corresponding to separation behavior. The blue arrows represent the reference velocity components corresponding to the attacker avoidance behavior. Thus, the reference velocity of individual in the security-based behavioral mode is actually the composite vector of the red velocity component and the blue velocity component. It can be seen that most individuals have only one reference velocity component (red or blue arrow), except for individuals 12 and 24 which need to consider both separation behavior and attacker avoidance behavior. From the individuals with blue arrows (such as individuals 18, 24 and 38), it is demonstrated that in order to avoid attackers, the individuals move towards the largest free space based on the observed projected view of the environment, rather than directly towards the opposite direction of the attacker. It should be noted that the reference velocities in Fig.3 are the results of considering the corresponding adaptive weight parameters, which are functions of light transmittance. For example, the reference velocity component for attacker avoidance (blue arrow) of individual 38 is greater than that of individual 2, because the light transmittance of individual 38 is 0.59, which is greater than that of individual 2 at t =21 s (shown in Fig.2(f)).

The minimum and maximum distance between the individuals of swarm with time is shown in Fig.4. As can be seen from Fig.4(a), the minimum distance between individuals has never been less than 2 m, so there is no collision between individuals during the movement. Due to the influence of the attacker, the maximum distance between individuals first increases and then decreases as shown in Fig.4(b). Moreover, the maximum distance between individuals can partially reflect the density of the whole swarm. The swarm changes from a dense state to sparse state and then back to a dense state, which is consistent with the change in maximum distance between individuals.

Fig.3. The reference velocities of individuals in different behavioral modes at t=21 s. (The small colored dots with an indexing number attached in the upper right corner represent the swarm individuals. The big black dots represent the attackers. The green arrows represent the reference velocities of individuals in the task-based behavioral mode. The red arrows represent the reference velocity components corresponding to the separation behavior. The blue arrows represent the reference velocity components corresponding to the attacker avoidance behavior).

Fig.4. The minimum and maximum distance between the individuals of swarm with time.

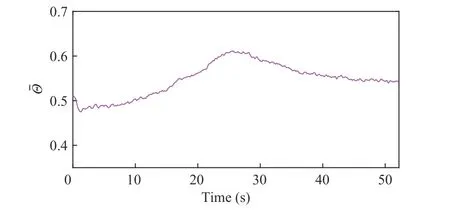
Fig.5. The average light transmittance of swarm.

VI. CONCLUSIONS

An autonomous control strategy has been presented in this paper for a swarm system under attack. The communication distance limitations faced by large-scale swarm systems have been solved by introducing the projected-view-based global interaction mechanism, which can ensure a fast swarm dynamic response and stable spatial cohesion in a complex environment. Moreover, the spatial freedom and the relative position in the swarm of each individual can be roughly represented by the defined light transmittance, which has been used to design the adaptive parameters of the autonomous control strategy. In the swarm simulation, the individuals avoided the attackers safely and regrouped without dispersion,which indicates that a swarm system with an autonomous control strategy has the ability to adapt to a dynamic environment and consider overall interests of the group.