Static-Output-Feedback Based Robust Fuzzy Wheelbase Preview Control for Uncertain Active Suspensions With Time Delay and Finite Frequency Constraint

Wenfeng Li, Zhengchao Xie, Jing Zhao, Pak Kin Wong, Hui Wang, and Xiaowei Wang

Abstract—This paper proposes a static-output-feedback based robust fuzzy wheelbase preview control algorithm for uncertain active suspensions with time delay and finite frequency constraint.Firstly, a Takagi-Sugeno (T-S) fuzzy augmented model is established to formulate the half-car active suspension system with consideration of time delay, sprung mass variation and wheelbase preview information. Secondly, in view of the resonation between human’s organs and vertical vibrations in the frequency range of 4-8 Hz, a finite frequency control criterion in terms of H∞ norm is developed to improve ride comfort.Meanwhile, other mechanical constraints are also considered and satisfied via generalized H2 norm. Thirdly, in order to maintain the feasibility of the controller despite of some state variables are not online-measured, a two stage approach is adopted to derive a static output feedback controller. Finally, numerical simulation results illustrate the excellent performance of the proposed controller.

I. INTRODUCTION

VEHICLE suspension systems play an important role in improving the vehicle chassis dynamic performance, such as ride comfort, handling stability and road holding capability[1]-[8]. Among various types of vehicle suspension systems,the active suspension system, consisting of traditional suspension components and advanced active vibration control mechanisms, has attracted substantial research efforts due to its flexibility in managing the tradeoff between the ride quality and mechanical constraints [9]-[11]. In order to improve vehicle dynamic performance, over the past decades, numerous control approaches have been presented for active suspension systems.Among various control methods, the H∞control concept has been widely applied to active suspensions in the context of robustness and disturbance attenuation [12], [13].

As the two basic problems encountered in the active suspension control, time delay and parameter uncertainties seriously limit the control performance and even cause system instability [12], [14]-[16]. As an excellent method to deal with the inherent parameter uncertainties existing in systems, Takagi-Sugeno (T-S) fuzzy model approach has been widely applied to the description of uncertain active suspension systems [13],[17]-[19]. Moreover, the fuzzy control gain is determined by offline calculated control gains and online calculated weighting factors, which can manage a better tradeoff between computational complexity and control performance. Based on T-S fuzzy model, many research results have been carried out to cope with the time delay via various delay-dependent Lyapunov functions, which are effective to guarantee the asymptotical stability of the closed-loop system and improve suspension performances [20], [21]. Thus, T-S fuzzy method is also adopted in this work to approximate the uncertain vehicle dynamic with consideration of time delay.

It is worth mentioning that the above methods are focused on the entire frequency range and ignore a vital fact that road disturbances belong to a finite frequency range. According to ISO-2631, the human’s organs are much sensitive to vertical vibrations of 4-8 Hz due to the severe harm resulted from resonation. In other words, more research efforts should be devoted to the issue of finite frequency constraint [22]. In[23]-[26], the state feedback control method was presented for active suspension systems in finite frequency range based on generalized Kalman-Yakubovich-Popov (KYP) lemma[27]. Given that some state variables cannot be measured online, the finite frequency output feedback control approach was investigated to maintain the feasibility of control strategies in the practical suspension system [28]-[30]. Owing to easy structure and convenient implementation, the analysis and synthesis of finite frequency static output feedback (SOF)control was presented to linear systems via a heuristic algorithm [31]-[33]. However, the inherent uncertainty or time delay is ignored in the above finite frequency output feedback control methods. Inspired by the heuristic algorithm,the finite frequency SOF control of uncertain active suspension systems with time delay and parameter variation is studied in this work.

Owing to that the utilization of road information contributes greatly to the improvement of suspension performance, much attention has been paid to preview control since its first presentation by Bender [34]. Compared with simple feedback control, preview control can acquire the preview information and prepare for the upcoming disturbances [35]. According to different ways to acquire the preview information, preview control can be divided into two categories: look-ahead preview[36], [37] and wheelbase preview [38]. As for look-ahead preview control, expensive laser sensors are required to obtain the preview information. In addition to the high cost of laser sensors, look-ahead preview also faces an inevitable drawback of distortion measurement, which may be resulted from rain water, bad weather, no luminosity and so on [39]. With regard to wheelbase preview, the disturbance of the front wheel is adopted as the preview information for the rear wheel [40].Based on wheelbase preview information, the rear suspension dynamic performances can be efficiently enhanced, which helps to improve the overall chassis performances. Without high cost of laser sensors and complex measurement, the wheelbase preview possesses more reliable and broad application prospects [39]-[42]. However, the finite frequency constraint is not discussed in the above wheelbase preview control methods. Hence, the combination of wheelbase preview information and the fuzzy SOF control is promising and still challenging for active suspension systems with time delay and finite frequency constraint, which is the main motivation of this work.

Motivated by the above concerns, a robust fuzzy wheelbase preview SOF control algorithm is proposed for uncertain halfcar active suspension systems with time delay and finite frequency constraint. Three featured contributions of this paper are summarized as follows:

1) T-S fuzzy model approach is applied to approximate uncertain suspension dynamics, in which uncertain parameters, time delay and wheelbase preview information are considered together.

2) A finite frequency criterion is proposed for control synthesis, which contributes to attenuate the targeted disturbance in the concerned frequency range.

3) A fuzzy wheelbase preview static output feedback control algorithm is proposed for uncertain active suspension systems,which eliminates the dependence on a full knowledge of the state vector.

The rest of this paper is organized as follows: Section II formulates a T-S fuzzy half-car active suspension model with parameter variation, time delay and wheelbase preview information. Further, a finite frequency control criterion is also proposed for controller design in Section II. Section III presents the main results of the proposed fuzzy wheelbase preview SOF control algorithm. Simulations with detailed analysis are presented in Section IV. Finally, Section V summarizes some useful conclusions of the research.

Notations: For a matrix P, PTand P－1denote its transpose and inverse, respectively. The notation P ＞0(≥0) means that the matrix P is a real symmetric and positive (semi-positive)matrix. To simplify notation, * is used to represent a block matrix which is readily inferred from symmetry in symmetric block matrices or complex matrix expressions. The diagonal matrix stands for a block-diagonal matrix.

II. SYSTEM MODELING AND PROBLEM FORMULATION

A. Half-car Active Suspension Model

To investigate suspension dynamics, a half-car active suspension model, as presented in Fig.1, is adopted in this work [43]. All symbol definitions shown in Fig.1 are listed in Table I. By assuming the vehicle pitch angle is small, the vertical motion of the suspension model can be described as follows:

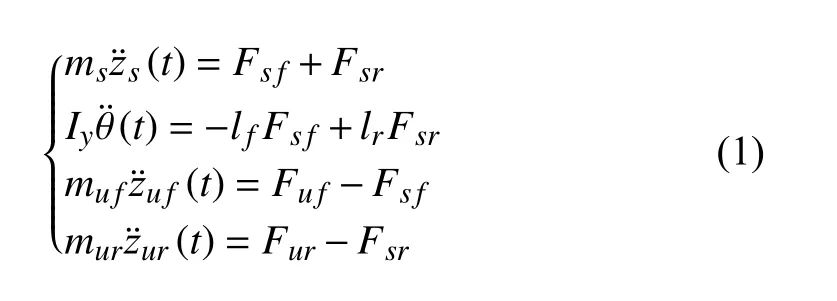
where

Fig.1. Half-car active suspension model.

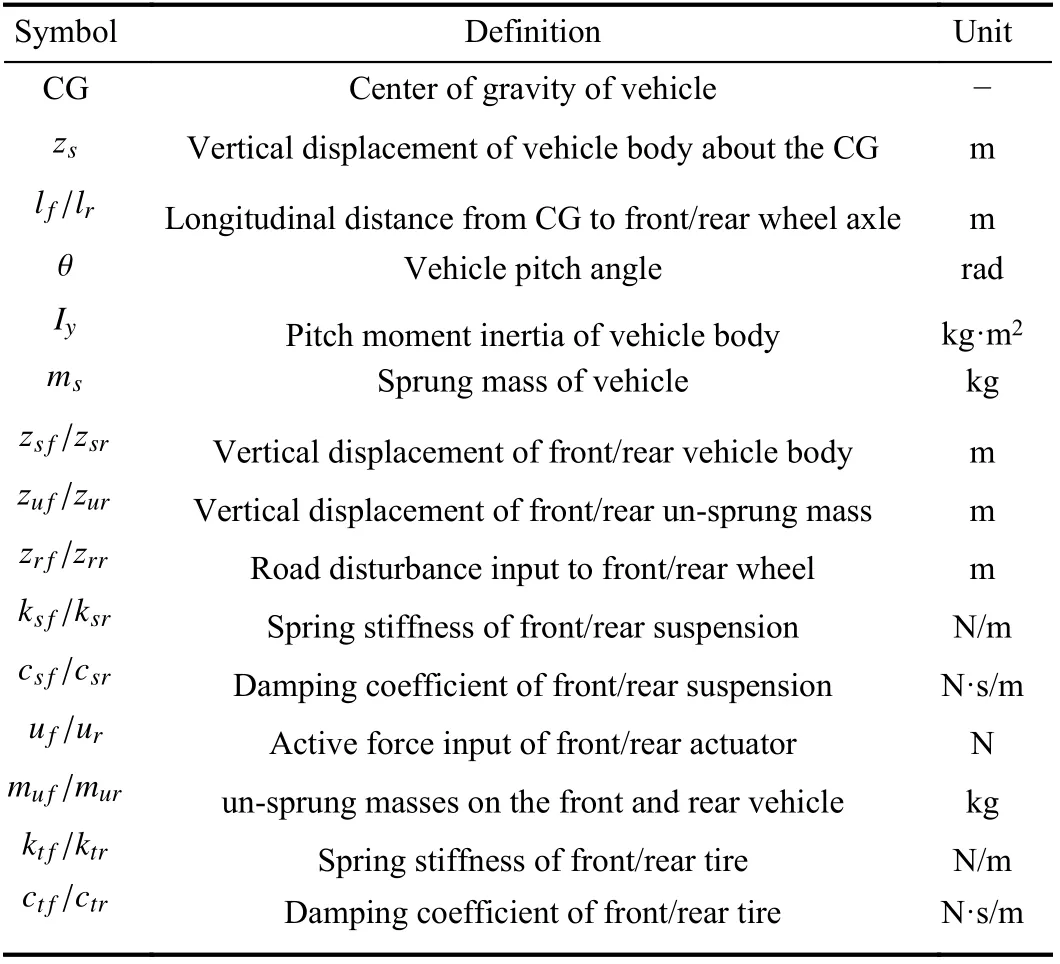
TABLE I SYMBOL DEFINITIONS OF ACTIVE SUSPENSION MODEL

It is convenient to choose the following state vector:

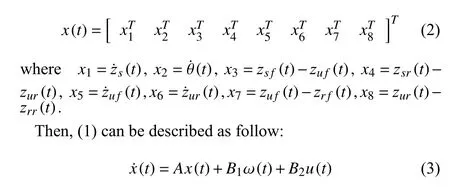
where

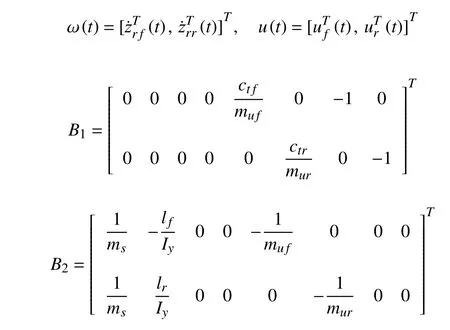
The main goal of active suspension systems is to improve ride comfort, guarantee a good handling stability and maintain an acceptable road holding capability. Generally speaking, a multi-objective control norm is widely applied to active suspension systems [39], [42].

2) H2norm is adopted to guarantee that mechanical hard constraints are satisfied to maintain good handling stability and road holding ability. Hence, the second controlled output is chosen as follows:

where z21(t) is the relative front suspension travel, z22(t) is the relative rear suspension travel, z23(t) is the relative dynamic front tire load, z24(t) is the relative dynamic rear tire load.

Then, the above two controlled outputs can be rewritten into the following state-space form:

According to Schur complement, (37) is equivalent to (29).

Proof: Based on (27) and (28), the following inequality can be obtained:

B. Parameterization of the Fuzzy SOF Control Gain

In light of (27)-(29), the parameterization of a fuzzy SOF controller is presented in following theorem.

Theorem 2: Considering the closed-loop system in (19): For given scalars τm＞0 , γ ＞0, ρ ＞0, ϖ1and ϖ2, the closed-loop system in (19) is asymptotically stable and satisfies the desired conditions in (20) and (21), if there exist positive definite matrices P1j, R1j, S1j, Qj, Zj, symmetric matrices Pj, Xj, and general matrices K, F, Ljsuch that the following conditions hold for i ,j=1,2:

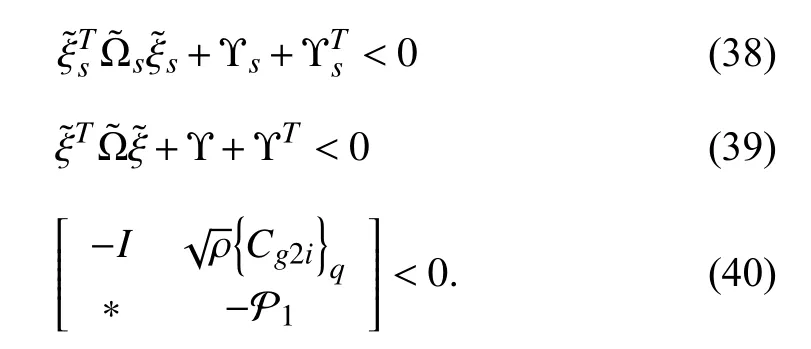
Moreover, the local output feedback control gains Kjcan be obtained as Ksofj=F－1Ljand the overall fuzzy SOF control gain can be obtained as follows:

where

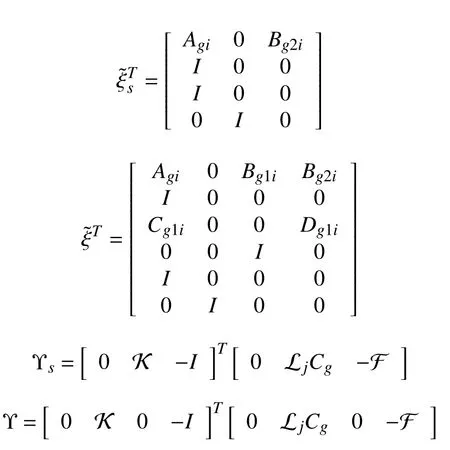
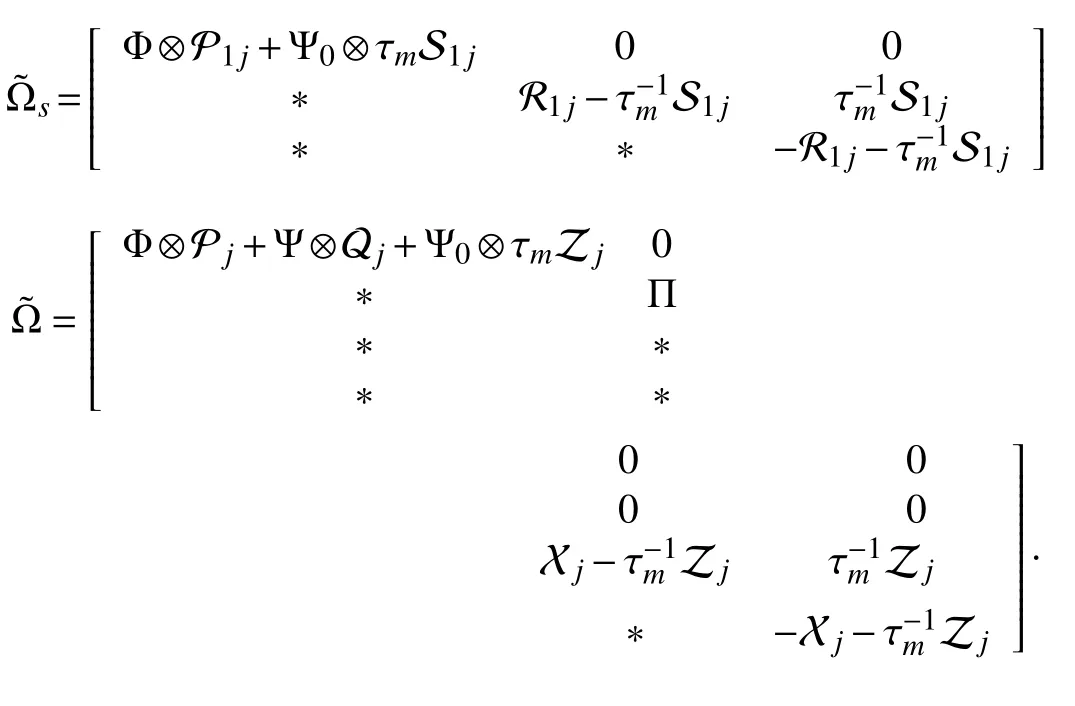
In other words, F is an invertible matrix. Then, the following useful substitutions are defined:

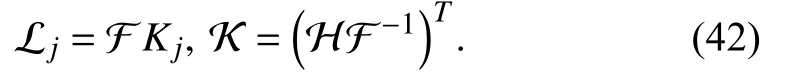
To further effectively deal with inherent uncertainties, the Lyapunov matrices and other related matrices are also replaced by the following parameter dependent forms:

Remark 2: Due to the existence of unknown matrix K, the conditions presented in Theorem 2 are not convex anymore.However, it should be noted that the conditions presented in Theorem 2 are become linear matrix inequalities, as long as the matrix K is priori and fixed.

C. Controller Optimization and Computation

Inspired by the two-stage approach presented in [31]-[33],the unknown matrix K can be fixed as a fuzzy finite frequency state feedback control gain. Therefore, first of all,the following theorem is presented to obtain an initial fuzzy finite frequency controller.

Theorem 3: Considering the closed-loop system in (19): For given scalars τm＞0 , γ ＞0, ρ ＞0, ϖ1, ϖ2and μ the closedloop system in (19) is asymptotically stable and satisfies the desired conditions in (20) and (21), if there exist positive definite matrices P1j, R1j, S1j, Qj, Zj, symmetric matrices Pj, Xj, and general matrices J, Vjsuch that the following conditions hold for i ,j=1,2:

Remark 3: In light of Theorem 3, an initial fuzzy finite frequency state feedback control gain can be computed (i.e.,Stage 1), which is essential to solving Theorem 2. Hence, the following convex optimization problem is proposed to find an optimal fuzzy SOF controller (i.e., Stage 2):

with K fixed as Ksfjcomputed by solving Theorem 3.

Then, the finite frequency fuzzy SOF controller is computed as

Remark 4: To highlight the effectiveness of the proposed controller (i.e., Controller I), a fuzzy SOF controller without wheelbase preview information can be easily obtained by solving (47) with system matrices replaced with original matrices, which is regarded as Controller II for comparative purpose. Moreover, the fuzzy finite frequency state feedback controller presented in [24] is also adopted as Controller III for comparative purpose. Compared with Controller III, a parameter-dependent Lyapunov function is employed in the derivation of the proposed Controller I, which contributes greatly to the reduction of conservativeness.

IV. SIMULATION RESULTS

In this section, some numerical simulations on a half-car active suspension model are carried out to evaluate and illustrate the performance of the proposed robust fuzzy wheelbase preview control strategy. The suspension parameters are listed in Table II. In particular, the uncertain sprung mass is assumed as 690±69sin(4/3πt)kg. Moreover,the online weighting factors are shown in Fig.3. The scalars for controller design are given as m=2, v=10 km/h , μ=50,τm=5 ms, ρ=0.81, ϖ1=4 Hz, ϖ2=8 Hz, the local control gains of the fuzzy SOF controller are obtained as follows:

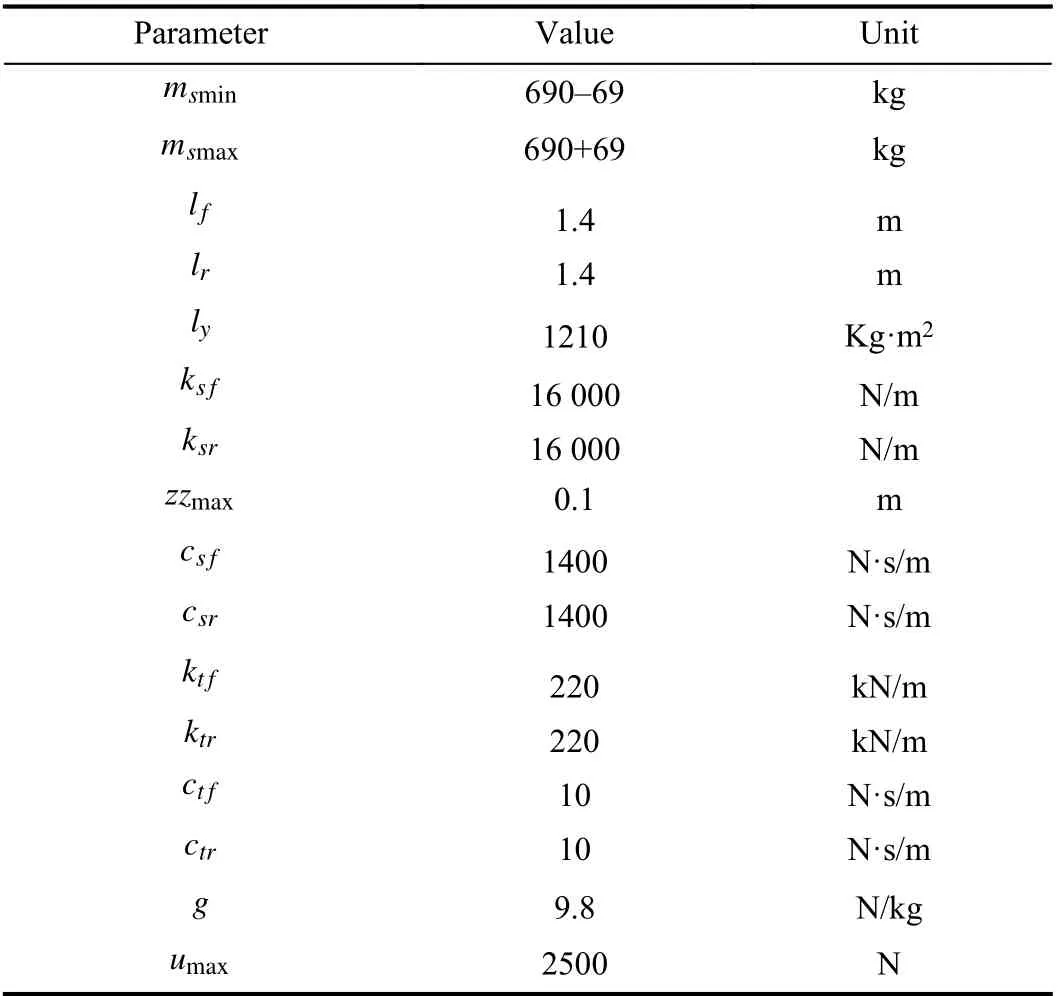
TABLE II PARAMETERS AND VALUES OF HALF-CAR SUSPENSION MODEL

Fig.3. Online weighting factors.

Moreover, the local control gains for Controller II can be obtained as follows:

Remark 5: A simple Lyapunov function and Jensen’s inequality are adopted in this work to derive a robust finite frequency control method for active suspension systems with time delay, which is effective but conservative to deal with the problem of controller design for time-delay systems. Hence,this paper focuses on a small time delay.

A. Frequency Response

Figs. 4 and 5 plot the frequency response results of body vertical acceleration and pitch angular acceleration when no time delay occurs. Fig.4 shows that Controllers I and II yield smaller body vertical acceleration and pitch angular acceleration compared with Controller III and passive suspension, especially in the frequency range of 4-8 Hz. Fig.4 also shows that Controller I generates a smaller pitch angular acceleration but a bigger body vertical acceleration compared with Controller II. Fig.5 shows that Controller I is more effective to attenuate the road disturbance input to rear tire than Controller II, which indicates the wheelbase preview controller contributes greatly to the improvement of rear suspension performances.

The frequency response results of body vertical acceleration and pitch angular acceleration with τ(t)=5 ms are plotted in Figs. 6 and 7. Fig.6 shows Controllers I and II generates smaller body vertical acceleration and pitch angular acceleration than that of Controller III and passive suspension,which means Controllers I and II can yield a better ride comfort. Fig.7 shows that Controller I excels Controller II in attenuation of the road disturbance input to rear tire. With the presence of time delay, Controllers I and II produce similar pitch angular acceleration, which means the superiority of wheelbase preview control degrades with the increase of time delay.

To summarize, frequency response results verify the robustness and effectiveness of the proposed Controller I.

B. Bump Response

A bumpy road is adopted to evaluate the performance of Controller I in time domain, which is shown as follows:

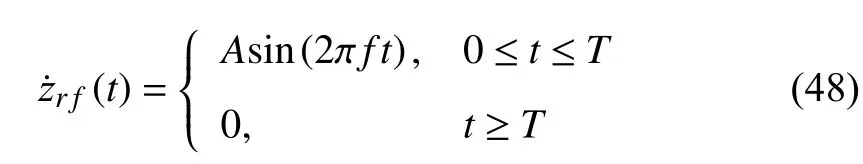
The bump response results when no delay occurs are plotted in Figs. 8-10. Fig.8 plots the results of the body vertical acceleration and the pitch angular acceleration, which shows that the values of body vertical acceleration and pitch angular acceleration with Controllers I and II are smaller than that with Controller III. It can also be seen from Fig.8 that Controller I is superior to Controller II in reduction of the road disturbance to rear tire, which verifies the effectiveness and importance of wheelbase preview control. Fig.9 plots the results of mechanical constraints, which are relative front suspension travel, relative rear suspension travel, dynamic front tire load and dynamic rear tire load. It is clear to see that all mechanical constraints are below than one, which indicates that mechanical hard constraints are guaranteed by all controllers. In addition, Fig.10 plots the results of actuator forces, which shows that both front actuator forces and rear actuator forces are less than the maximum 2500 N and feasible to realize.

Fig.4. Frequency response results for: (a) body vertical acceleration, (b) pitch angular acceleration from z r f(t) without delay.

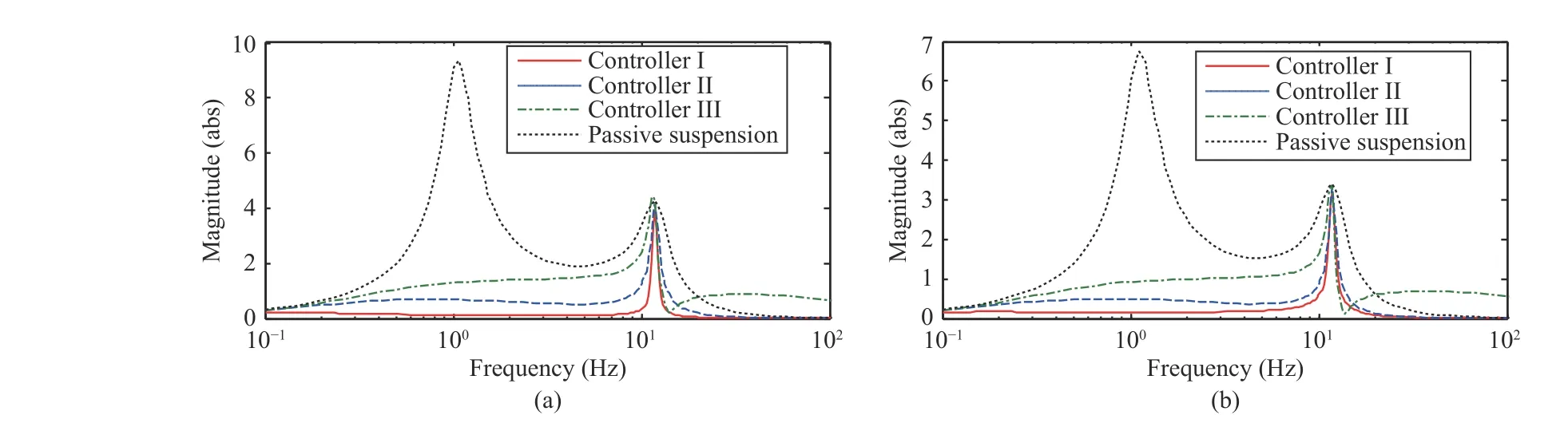
Fig.5. Frequency response results for: (a) body vertical acceleration, (b) pitch angular acceleration from z rr(t) without delay.

Fig.6. Frequency response results for: (a) body vertical acceleration, (b) pitch angular acceleration from z r f(t) with τ (t)=5 ms.

Fig.7. Frequency response results for: (a) body vertical acceleration, (b) pitch angular acceleration from z rr(t) with τ (t)=5 ms.

Fig.8. Time-domain response results for: (a) body vertical acceleration, (b) pitch angular acceleration without delay.

The bump response results when τ(t)=5 ms are plotted in Figs. 11-13. Fig.11 exhibits that Controllers I and II are more effective to reduce body vertical acceleration and pitch angular acceleration than Controller III. Moreover, Fig.11 shows Controller I is more effective to attenuate the road disturbance to rear tire than Controller II. Fig.12 shows that all mechanical hard constraints are lower than one, which means all controllers can guarantee the mechanical constraints be satisfied. Fig.13 illustrates control inputs are less than the maximum one, which indicates the actuator forces are feasible to generate.

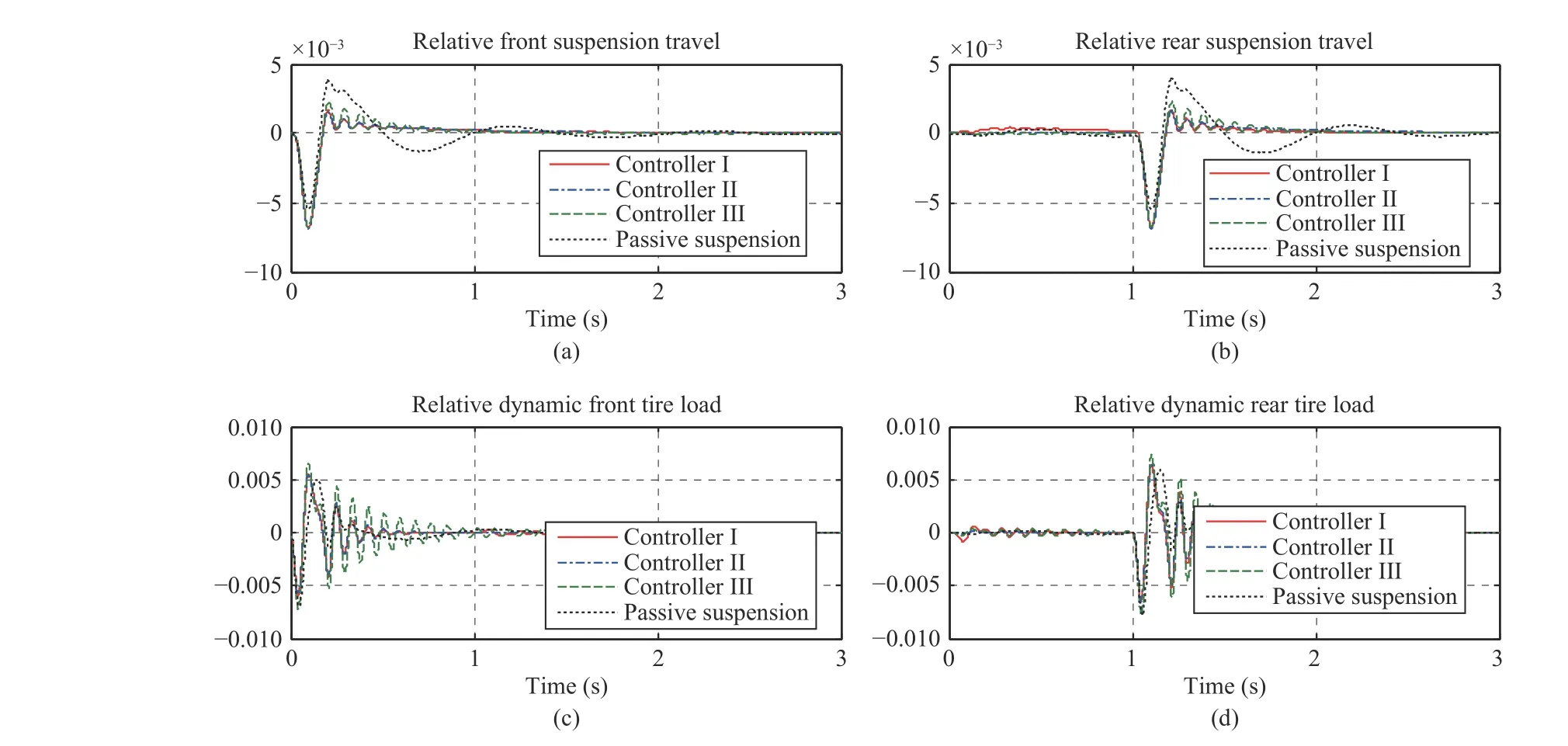
Fig.9. Time-domain response results for: (a) relative front suspension travel, (b) relative rear suspension travel, (c) dynamic front tire load, (d) dynamic rear tire load without delay.

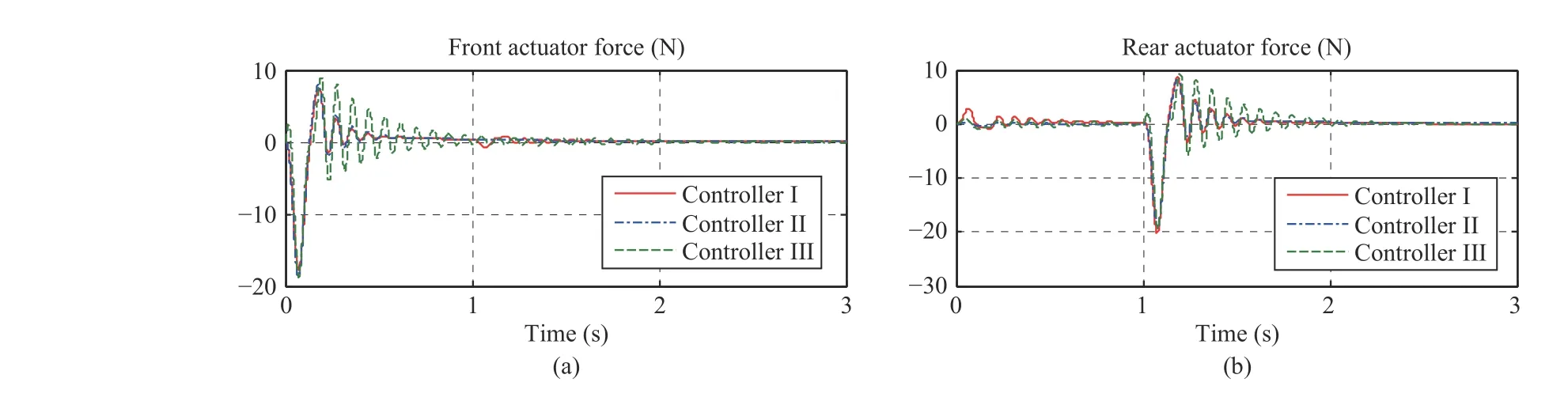
Fig.10. Time-domain response results for: (a) front actuator force, (b) rear actuator force without delay.

Fig.11. Time-domain response results for: (a) body vertical acceleration, (b) pitch angular acceleration with τ (t)=5 ms.

To clear show the performance of the proposed controller,the root mean square (RMS) value under the above bump road disturbance is presented in Tables III-VI, which is calculated as [25]

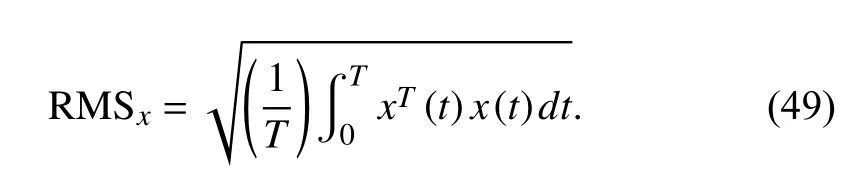
Tables III-VI shows that Controllers I and II yield smaller RMS values of body vertical acceleration and pitch angular acceleration than that produced by Controller III and passive suspension. Moreover, Controller I is more effective to yield smaller RMS values of body vertical acceleration and pitch angular acceleration compared with Controller II, which verifies the effectiveness of wheelbase preview control.

In a word, the bump response results illustrate that Controller I can effectively achieve a better ride quality even in the occurrence of time delay and parameter variation.

V. CONCLUSIONS

In this research, a robust fuzzy wheelbase preview SOF controller is proposed for uncertain half-car active suspension system with time delay and finite frequency constraint.Compared with the previous study presented in [24], the proposed wheelbase preview fuzzy control strategy possesses higher effectiveness. Some useful conclusions are listed as follows:

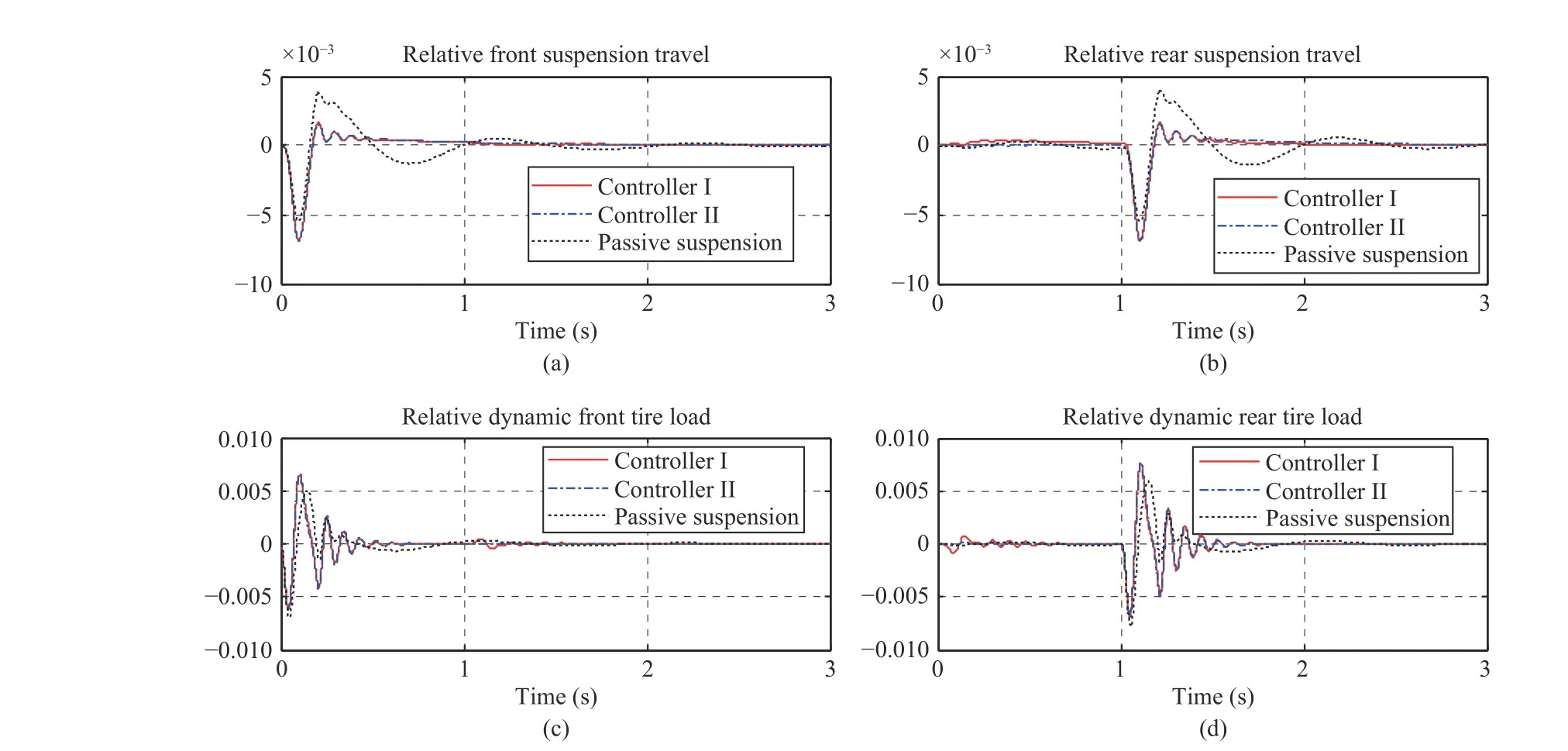
Fig.12. Time-domain response results for: (a) relative front suspension travel, (b) relative rear suspension travel, (c) dynamic front tire load, (d) dynamic rear tire load with τ (t)=5 ms.

Fig.13. Time-domain response results for: (a) front actuator force, (b) rear actuator force with τ (t)=5 ms.

TABLE III RMS VALUES OF BODY VERTICAL ACCELERATION WITHOUT DELAY

TABLE IV RMS VALUES OF PITCH ANGULAR ACCELERATION WITHOUT DELAY

TABLE V RMS VALUES OF BODY VERTICAL ACCELERATION WITH DELAY

1) The proposed T-S fuzzy control is effective to deal withnonlinear active suspension dynamics. Moreover, a parameter dependent Lyapunov function contributes greatly to further reduce conservativeness.

TABLE VI RMS VALUES OF PITCH ANGULAR ACCELERATION WITH DELAY

2) Wheelbase preview is helpful to attenuate the road disturbance to rear tire, which provides a potential way to improve the overall suspension performance.

3) A two-stage method is proposed to solve the static output feedback control, which eliminates the dependence on a full knowledge of the state vector.

Given that this paper mainly focuses on constant vehicle velocity, more future research efforts will be devoted to investigate less conservative results for wheelbase preview control of active suspension systems with time delay and varying velocity [41].