DC Motor Speed Regulator via Active Damping Injection and Angular Acceleration Estimation Techniques
2021-04-16SeokKyoonKimandChoonKiAhnSeniorMemberIEEE
Seok-Kyoon Kim and Choon Ki Ahn, Senior Member, IEEE
Abstract—This paper suggests a novel model-based nonlinear DC motor speed regulator without the use of a current sensor.The current dynamics, machine parameters and mismatched load variations are considered. The proposed controller is designed to include an active damping term that regulates the motor speed in accordance with the first-order low-pass filter dynamics through the pole-zero cancellation. Meanwhile, the angular acceleration and its reference are obtained from simple first-order estimators using only the speed information. The effectiveness is experimentally verified using hardware comprising the QUBEServo2, myRIO-1900, and LabVIEW.
I. INTRODUCTION
SERVO systems driven by a DC motor (DCM) have a wide range of industrial applications, such as in mobile robots and manufacturing machines. High transient performance and robustness are required to meet application specifications in the presence of practical constraints such as machine parameter and load variations. Fortunately, the servo system performance can be greatly improved by implementing a DCM controller with advanced identifiers (as in [1]-[7]),which updates the parameter estimates to make the control error variables vanish exponentially.
Traditionally, the speed regulation task of industrial motors,including DC and AC types, has been accomplished by a proportional-integral (PI) controller with only speed error feedback, ignoring the transient current behavior; this provided easy implementation but limited performance. The cascade strategy has been suggested for a better performance,which comprises inner-loop current control with a high cut-off frequency and outer-loop speed control with a low cut-off frequency. PI controllers are often adopted for each loop with properly adjusted feedback gains via trial-and-error, Bode,and Nyquist techniques [8], [9]. A novel self-tuning PI controller that minimizes the cost function has been suggested to solve the feedback gain-tuning problem [10]. A nonlinear control technique has been applied to the inner loop with the motor parameter-dependent compensation term and feedback gain, rendering the closed-loop behavior in the form of the first-order low-pass filter (LPF) [11], [12]. Several advanced techniques such as integral back-stepping, neural networks,and feedback linearization, combined with parameter adaptation laws have been devised to attenuate disturbances from parameter and load variations [13]-[20]. A reduction in the number of sensors has been accomplished using the Luenberger observer and Kalman filtering techniques with motor parameter dependency [21]. The parameter dependence of estimators has been alleviated by designing an adaptive observer with a projection algorithm-based estimator for lumped parameters [15] and a sliding-mode observer with a flux estimator using the classical direct adaptive control technique [22].
This study suggests an advanced speed control technique considering the current dynamics without current feedback,which widens the closed-loop cut-off frequency range without requiring an additional current sensor. This makes two contributions. First, the introduction of an active damping term and a DOB stabilizes the angular velocity and acceleration, which yields the first-order closed-loop transfer function via pole-zero cancellations. Second, the parameterindependent estimator is designed to make the angular acceleration available for feedback. The resultant control and estimators do not require the true value of DCM parameters.The closed-loop analysis results are also provided for an academic contribution through the Lyapunov stability criterion. Using the hardware setup of the QUBE-Servo2,myRIO-1900, and LabVIEW, the experimental study clearly shows a performance improvement compared with recent DOB-based (in [11]) and feedback-linearization (FL)controllers.
II. PRELIMINARY
A. DCM Dynamics
The following second-order differential equations describe the DCM speed and current dynamics [23]:
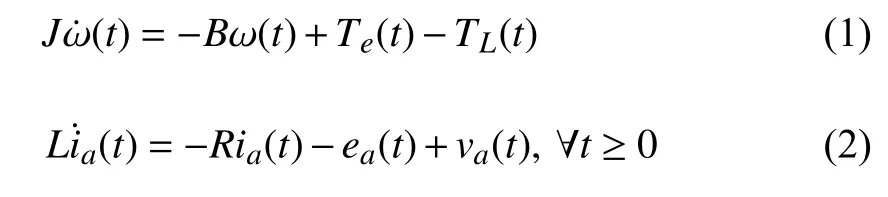
with the state variables denoted as ω(t) (speed) and ia(t)(stator current) and the control input given as va(t) (stator voltage). The electrical torque Te(t) and back EMF ea(t)couple the mechanical and electrical dynamics, which are given by Te(t)=kTia(t) and ea(t)=keω(t) with the coefficients kT>0 and ke>0. The load torque TL(t) acts as an unmatched external disturbance that can be abruptly changed in accordance with the load conditions. The remaining DCM coefficients are given as; J : rotor inertia, B : viscous damping, L : stator inductance, and R : stator resistance.
B. Problem Formulation

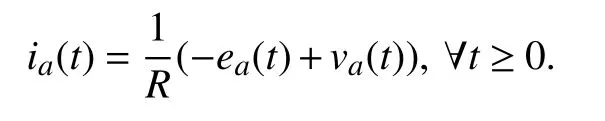
This assumption results in a control law simplification but there is a chance of limiting the closed-loop cut-off frequency for some applications. To solve this problem, the current dynamics (2) must be considered in the controller design task,which causes the increment of the closed-loop system order(leading to undesirable overshoots) and sensor for current feedback (requiring a parameter-dependent observer, such as the Luenberger type). This study handles these two challenges by incorporating the parameter-independent angular acceleration estimator and estimator-based active-damping injection causing the pole-zero cancellation.
III. CONTROLLER DESIGN

A. Angular Acceleration Estimator
The proposed controller needs to feed back the angular acceleration of a(t):= ω˙(t) which can be obtained through the direct differentiation involved in high-frequency noisy component magnification. To avoid this operation, this section suggests the estimation algorithm for angular acceleration a(t)

where the design parameter la>0 determines the disturbance convergence rate.
Note that the proposed estimator (6) and (7) makes both the acceleration error feedback and active damping injection available online without DCM true parameter dependence,which corresponds to the advantage from the conventional Luenberger-type observer using the speed dynamics (1).Section III-C analyzes the exponential convergent behaviors of the estimation variable a ˆ(t).
B. Control Law
The additional differentiation (4) and substitution of (5)with (4) results in the angular acceleration dynamics

with the gain lω>0. Fig.1 shows the control system structure.Note that, except for the design constants of la(the estimator),Bd, ωsc(the controller), and lω(the DOB), all other symbols are treated as variables in Section III-C.
C. Analysis
This section begins with the angular acceleration and its reference estimation behavior analysis in Theorem 1.
Lemma 1: The proposed estimator (6) and (7) behaves according to the first-order LPF dynamics:
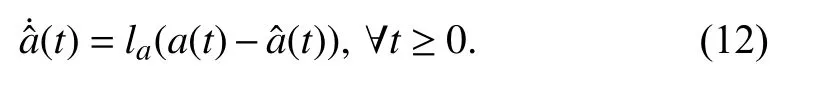



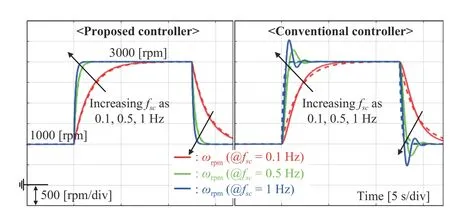
Fig.3. Speed-tracking performance variations for various cut-off frequencies: fsc=0.08,0.1,0.3 Hz.
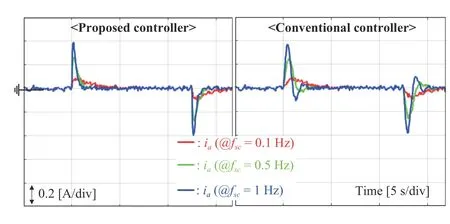
Fig.4. Current behavior comparison in speed-tracking task.
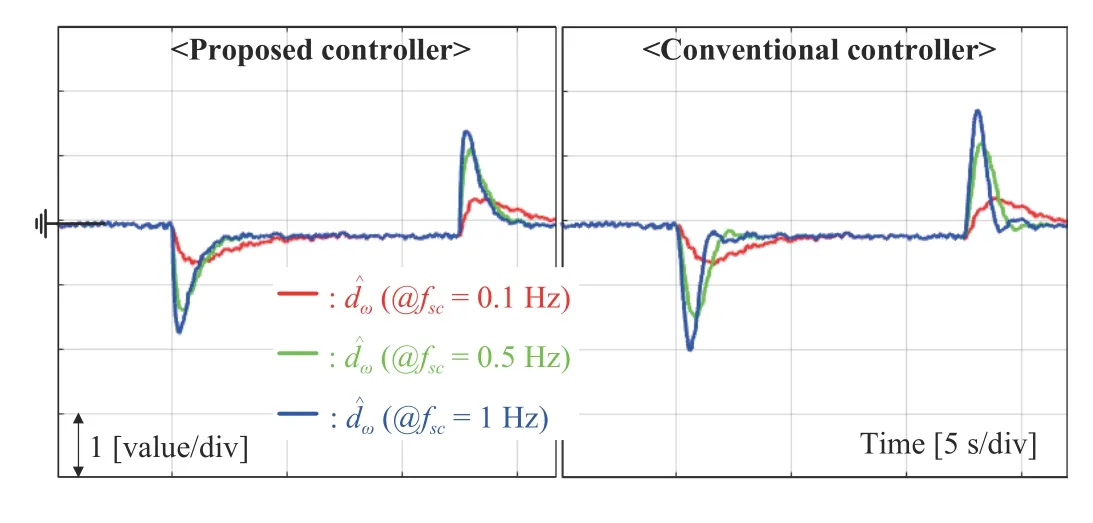
Fig.5. DOB behavior comparison in speed-tracking task.
2) Regulation Task: This section presents the performance comparison results for the speed regulation task in the 1 000 rpm operation mode. For this, a pulse-type load torque of TL=0.001 Nm was abruptly applied and the three cut-off frequencies used in the previous experiment were assigned to the closed-loop system. A considerable speed recovery performance improvement can be observed in Fig.6 for several operating modes. Fig.7 shows the current responses with over/undershoot reduction by the proposed controller.
B. Comparison With Cascade-Type FL Controller
1) Tracking Task: This subsection presents another speedtracking performance comparison result with the FL controller in the same experimental scenario as Section IV-A. Fig.8 shows that the proposed controller without the current sensor still improved the closed-loop robustness compared with the cascade-type FL controller for several cut-off frequencies.Similar to the previous comparison, Fig.9 reveals the rapid current responses by the proposed controller with reduced over/undershoots.
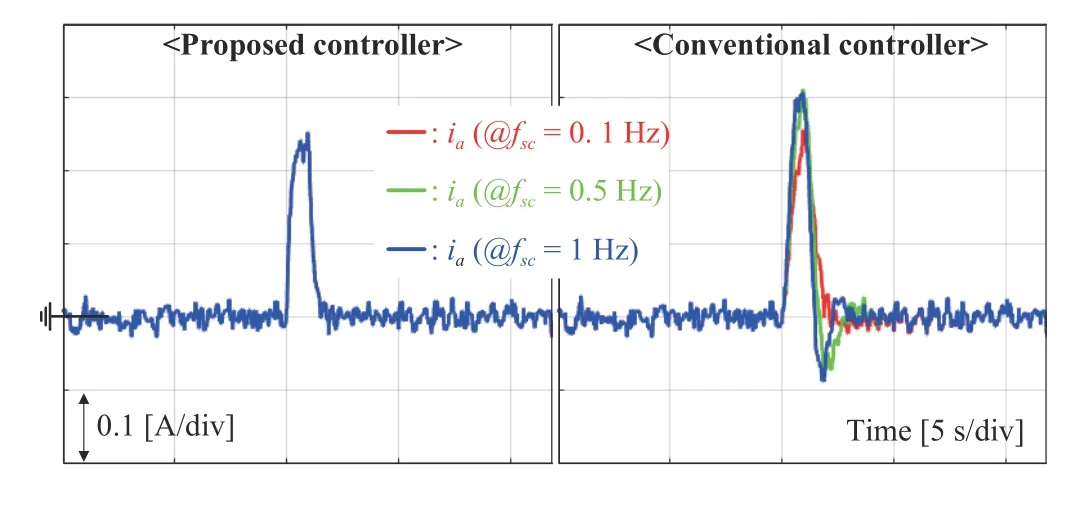
Fig.7. Current behavior comparison in speed regulation task for pulse-type load torque of T L=0.001 Nm.
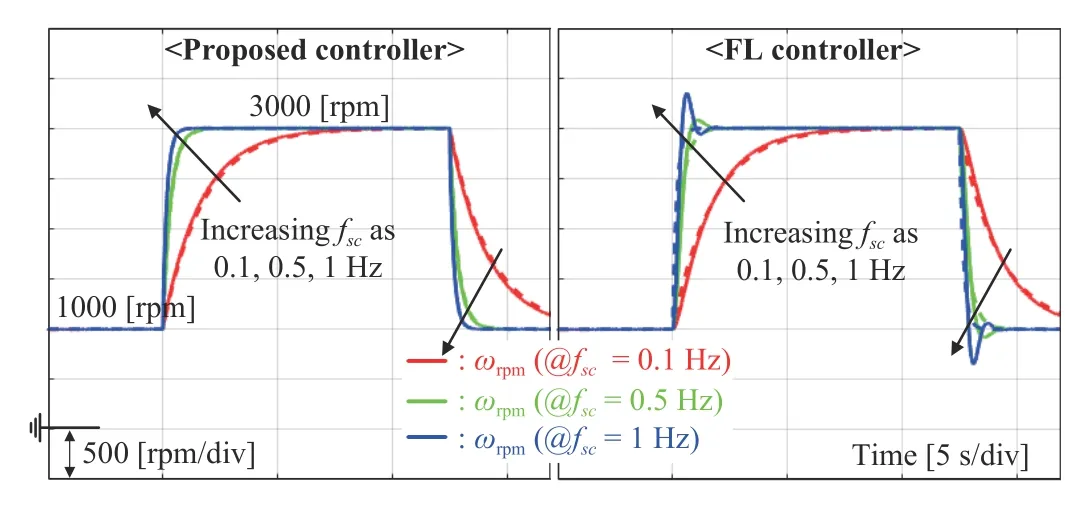
Fig.8. Speed-tracking performance comparison with cascade-type FL controller for several cut-off frequencies: fsc=0.08,0.1,0.3 Hz.
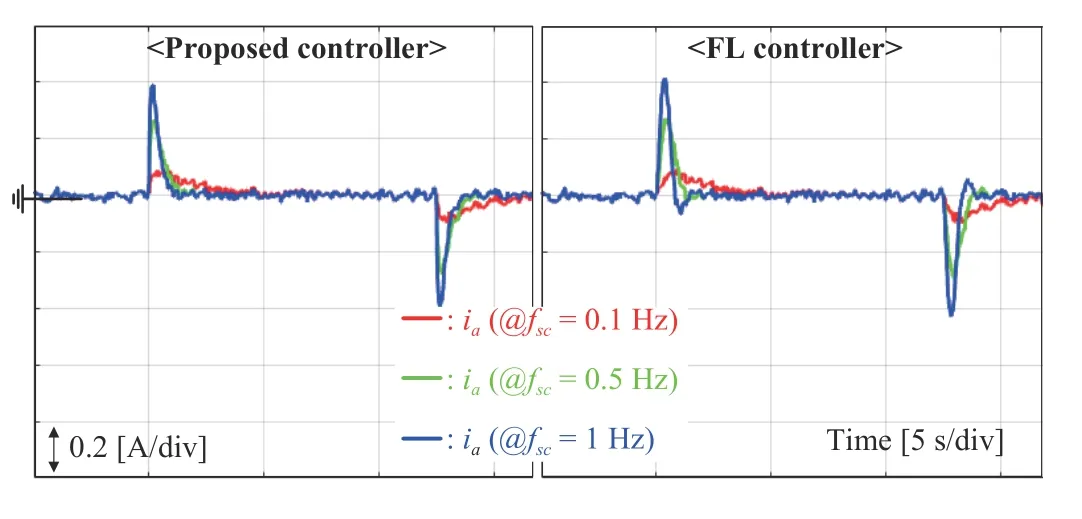
Fig.9. Current behavior comparison with cascade-type FL controller in speed regulation task.

Fig.10. Speed regulation performance variation comparison with cascadetype FL controller for pulse-type load torque of T L=0.001 Nm.
2) Regulation Task: Fig.10 presents another speed regulation performance comparison result with the cascadetype FL controller. This shows the significant superiority of the proposed controller due to reduced over/undershoots with consistent closed-loop performance for different cut-off frequencies, compared with the FL controller. Similar to the previous comparison, Fig.11 displays rapid current responses by the proposed controller with reduced over/undershoots.

Fig.11. Current behavior comparison with cascade-type FL controller in speed regulation task for pulse-type load torque of T L=0.001 Nm.
V. CONCLUSION
This paper has suggested a novel DOB-based speed control technique for industrial servomotor applications considering load and parameter uncertainties. The proposed estimators have been constructed to make the angular acceleration and its reference admissible for feedback. The controller has been devised with the active damping injection technique to stabilize the angular acceleration dynamics robustly by incorporating the resultant estimators and DOBs. The experimental study has verified the effectiveness of the proposed scheme in realistic scenarios. A future study will extend the proposed technique to large-scale motor systems with systematic control system-tuning guidelines.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Ground-0 Axioms vs. First Principles and Second Law: From the Geometry of Light and Logic of Photon to Mind-Light-Matter Unity-AI&QI
- Deep Learning for EMG-based Human-Machine Interaction: A Review
- Distributed Secondary Control of AC Microgrids With External Disturbances and Directed Communication Topologies: A Full-Order Sliding-Mode Approach
- Deep Learning in Sheet Metal Bending With a Novel Theory-Guided Deep Neural Network
- Autonomous Control Strategy of a Swarm System Under Attack Based on Projected View and Light Transmittance
- Computing Paradigms in Emerging Vehicular Environments: A Review
