Observer-Based Adaptive Fuzzy Tracking Control Using Integral Barrier Lyapunov Functionals for A Nonlinear System With Full State Constraints
2021-04-16WeiZhaoYanjunLiuSeniorMemberIEEEandLeiLiuMemberIEEE
Wei Zhao, Yanjun Liu, Senior Member, IEEE, and Lei Liu, Member, IEEE
Abstract—A new fuzzy adaptive control method is proposed for a class of strict feedback nonlinear systems with immeasurable states and full constraints. The fuzzy logic system is used to design the approximator, which deals with uncertain and continuous functions in the process of backstepping design. The use of an integral barrier Lyapunov function not only ensures that all states are within the bounds of the constraint, but also mixes the states and errors to directly constrain the state, reducing the conservativeness of the constraint satisfaction condition.Considering that the states in most nonlinear systems are immeasurable, a fuzzy adaptive states observer is constructed to estimate the unknown states. Combined with adaptive backstepping technique, an adaptive fuzzy output feedback control method is proposed. The proposed control method ensures that all signals in the closed-loop system are bounded, and that the tracking error converges to a bounded tight set without violating the full state constraint. The simulation results prove the effectiveness of the proposed control scheme.
I. INTRODUCTION
IN the last few years, the problem of uncertainty in nonlinear systems [1]-[3] is widely discussed by scholars,many methods are proposed to dispose unknown parameters in nonlinear systems. It has been shown that fuzzy logic systems (FLSs) [4] and neural networks (NNs) [5], [6], as available approximation methods, play an important role in adaptive [7]-[9] backstepping design. Furthermore, FLSs and NNs provide a novel solution for tracking or regulating control problems of nonlinear systems. For example, in [10],by using NNs, the neural adaptive fault tolerant control method with multi-objective constraints is designed. Besides,NNs are involved to counter of unknown external disturbance and functions [11]. The fuzzy adaptive control strategy is employed to deal with uncertain and continuous functions of electric vehicle systems in [12]. In [13], for nonlinear systems with unknown functions, an adaptive NN control approach is developed. According to FLSs and NNs, some effective control algorithms are presented for nonlinear single-input single-output (SISO) systems in [14]. Subsequently, some scholars have made great efforts for the adaptive control design of uncertain nonlinear multi-input multi-output(MIMO) systems in [15]. However, it should be noted that the above research results ignore the influence of constraints in nonlinear systems.
As we all know, constraints are inevitable and widespread in actual systems, such as with a non-uniform gantry crane [16],robotic manipulator [17], proximity operations [18],mechanical assemblies [19], etc. If there are no constraints, it may make the system unable to operate, and could lead to more serious consequences. Therefore, many effective control methods are proposed to deal with constraints, including the model predictive method [20] extreme-seeking control [21],and prescribed performance control [22]. In addition, in order to ensure that the constraints are never violated, the barrier Lyapunov function (BLF) is first proposed in [23]. Since then,the BLF has been used by many researchers as a main tool for solving constraints. In [24], by combining the BLF with the backstepping technique, the controller and adaptive laws with full state constraints and input time-delay are designed. The BLF is also used for a MIMO nonlinear system with full state constraints in [25]. For MIMO asymmetric full state constraints, considering the feasibility conditions of the virtual controller, a new nonlinear transformation function is proposed in [26]. Thereby, the feasibility condition in the virtual controller is eliminated. In [27], an adaptive control strategy with output constraint is proposed. The article [28]considers the state constraints of stochastic system with unknown time-delay by using BLF and NNs. However, it is important to note that the above studies are all about constant constraints. The constant constraint is just an exceptional case of the time-varying constraint [29]. In order to have more extensive research on constraints, many scholars study the time-varying constraints. In [30], the authors use asymmetric BLF to dispose the issue of time-varying state constraints. An intelligent tracking controller with a time-varying output constraint is designed in [31].
The above BLF-based state constraints research the constraints of errors, rather than constrain the states, and must clearly identify the boundaries of the virtual controller. This will cause conservative feasibility conditions for constraint satisfaction. Inspired by the integral barrier Lyapunov function (iBLF) [32], [33], this paper proposes a new iBLF to solve the state constraints. Compared with logarithmic barrier Lyapunov functions and tangent barrier Lyapunov functions,our proposed new iBLF mixes states with errors, so that the iBLF can be designed for direct execution of the constraints of the original states. In [34], using iBLF, the controller and adaptive law of the nonlinear switched system with full state constraints are constructed. Hence, the conservatism of BLF with error constraints is well avoided. By using NNs and iBLF, the full state constraints of uncertain nonlinear strict feedback systems with unknown dynamics are processed in[35], in which the iBLF is adopted to handle the state constraints directly. By avoiding indirectly imposing constraints on errors, which would introduce a certain degree of conservativeness, in this article, we do our best to overcome this shortcoming and relax the feasibility conditions. However, whether it is based on BLF or iBLF constraints, state variables are all measurable. As we all know,state variables are often immeasurable in actual systems, how to resolve the condition of untestable state in this paper is another challenge we have to face.
Over the last few years, the fuzzy adaptive control method with an observer has received widespread attention and achieved many important results. It should be noted that as far as linear systems are concerned, many researchers combine state feedback controllers with state observers to resolve the output feedback control problem. However, the above method is not suitable for nonlinear systems. Therefore, the observerbased adaptive fuzzy adaptive control method is better studied for nonlinear systems. Aimed at an uncertain nonlinear SISO affine system, due to the approximation ability of the fuzzy logic system, an adaptive control method with a state observer is proposed in [36]. In [37], for nonlinear SISO non-affine systems, the direct adaptive output feedback controller based on a fuzzy logic system is designed. However, these observer designs based on fuzzy logic systems are only suitable for SISIO systems. In actual engineering, most systems are MIMO. In [38], [39], for nonlinear MIMO systems, fuzzy backstepping methods are used to construct observers to deal with unmeasured states. As far as we know, although the observer-based adaptive fuzzy output feedback control method has achieved many results, there are few research results involving the adaptive fuzzy output feedback backstepping controller for iBLF constraints.
Inspired by the above research, an adaptive fuzzy output feedback control method is proposed for uncertain nonlinear systems with unknown functions. The fuzzy approximation ability is used to approximate uncertain and continuous functions. In the meantime, an intelligent controller is designed to achieve the desired control goal. The main contributions of this article are as follows:
1) So as to handle the full state constraints better, a new iBLF is constructed in this paper. By adopting iBLF, not only is the problem of full state constraints solved, but also the state is directly constrained, which avoids the known conservative condition of the transition error.
2) The fuzzy adaptive observer is constructed to deal with the unknown states of nonlinear system. What is more,combining iBLF with backstepping methods, and using the properties of fuzzy basis functions and bounded control design technology, an adaptive fuzzy output feedback control based on observer is proposed.
3) The adaptive output feedback strategy proposed in this paper can not only ensure that the signal in the closed-loop system is bounded, but also the observer error and tracking error converge to zero in a small neighborhood. Simulation results prove the effectiveness of the proposed control scheme.
The specific organization of this paper is as follows. First, a fuzzy adaptive observer with output feedback is designed in Section II. Then, the detailed procedure of iBLF derivation for dealing with full state constraints is given, in which the adaptive controller and the adaptive laws are designed in Section III. Finally, simulation results prove the feasibility of the proposed control algorithm in Sections IV, and in Section V,conclusions are given.
II. PRELIMINARIES AND PROBLEM FORMULATION
A. System Description
Consider the following SISO nonlinear system








where m=0.02 , g=9.8, l=1, B=1, M=0.5. The rest of the design parameters are the same as Case 1.
From Figs. 6-10, it can be seen that the simulation results on the single link robot system are similar to those of the nonlinear system. Therefore, the algorithm proposed in this paper can also be applied in the practical system.
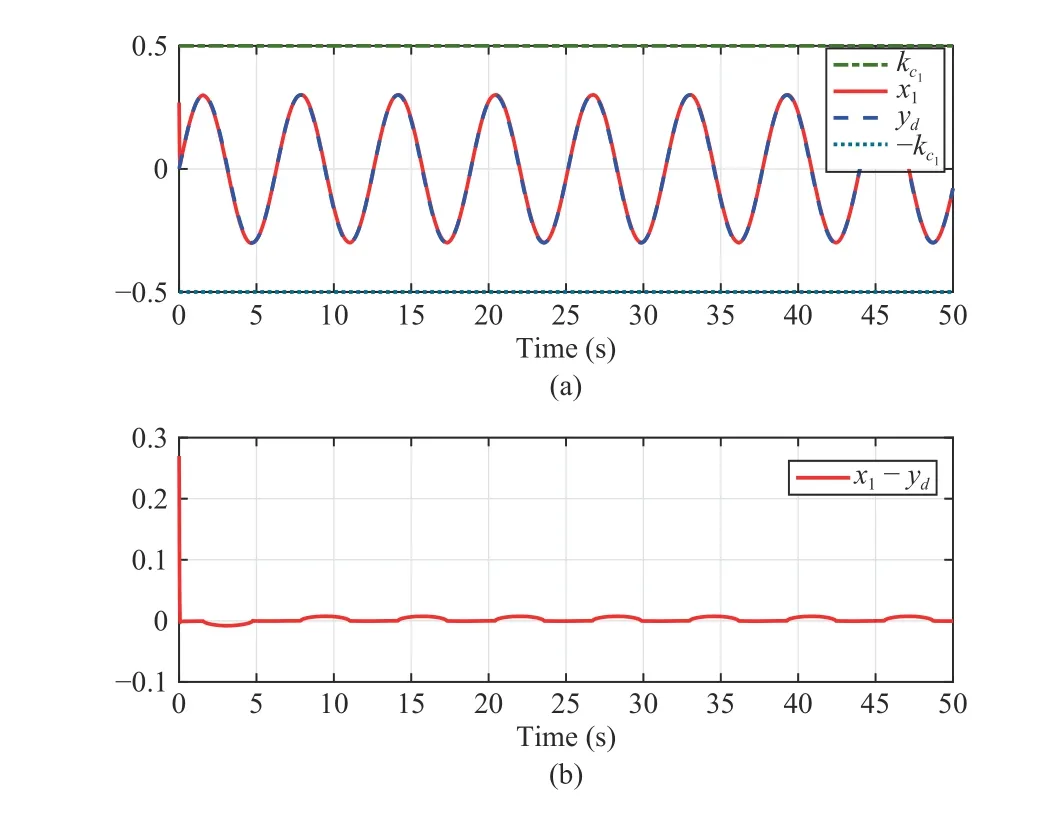
Fig.1. State x1 tracking and tracking error in Case 1. (a) Trajectory of x1,yd and constraint interval; (b) Trajectory of tracking error.
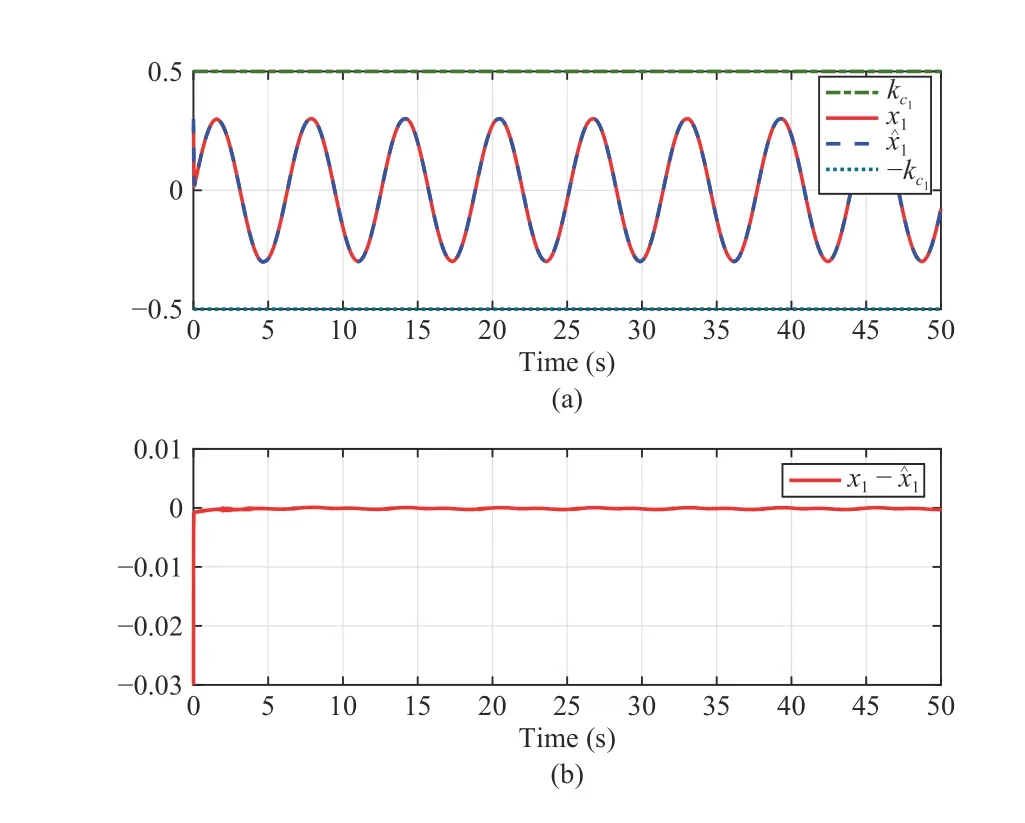
Fig.2. Observation and error of state x1 in Case 1. (a) Trajectory of x1 , and constraint interval; (b) Trajectory of estimation errors xˆ1.
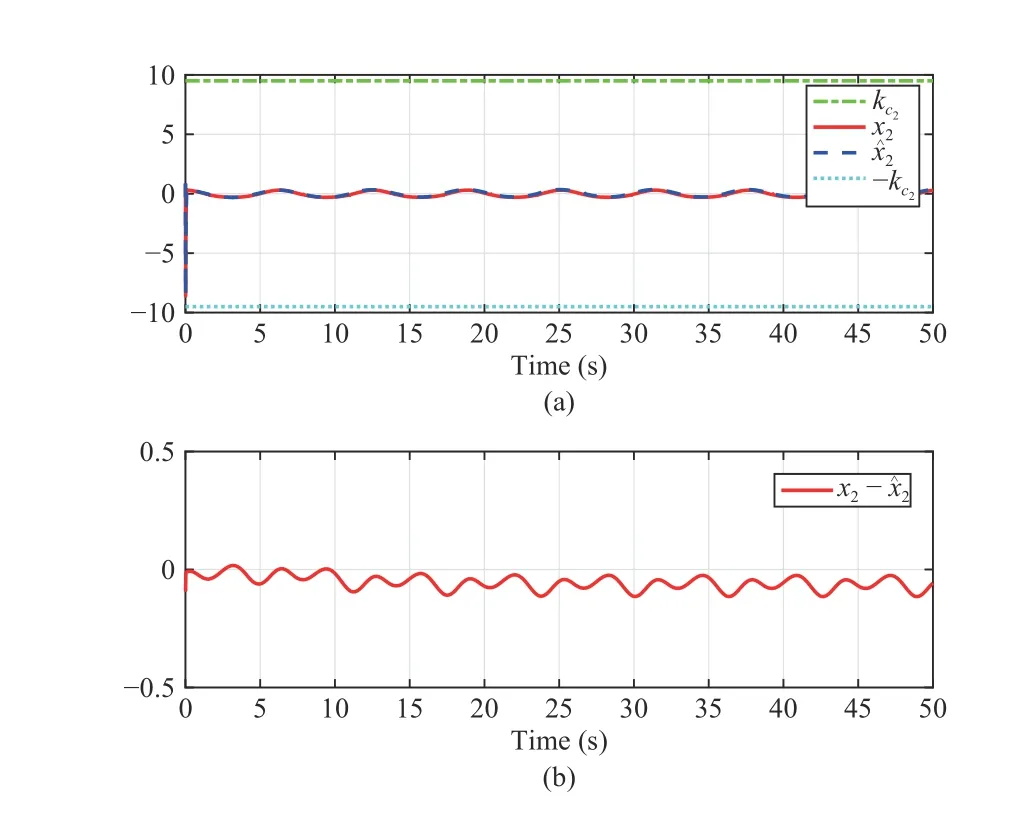
Fig.3. Observation and error of state x2 in Case 1. (a) Trajectory of x2 , and constraint interval; (b) Trajectory of estimation errors .
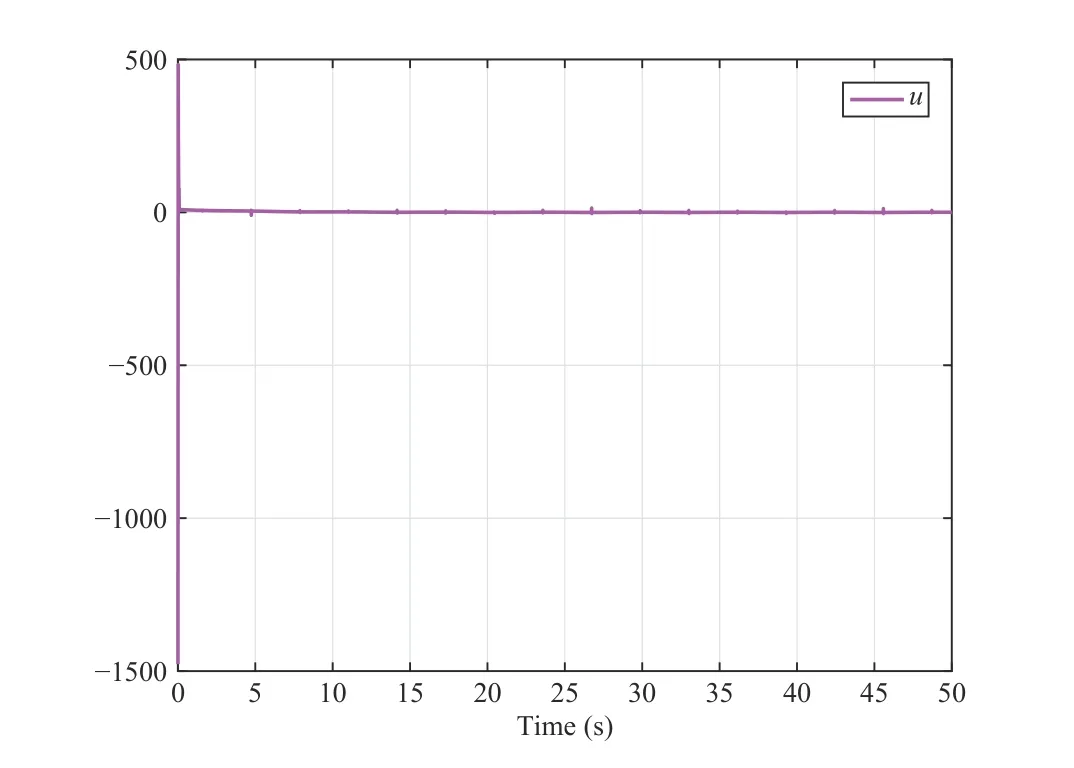
Fig.4. Trajectory of system input u in Case 1.
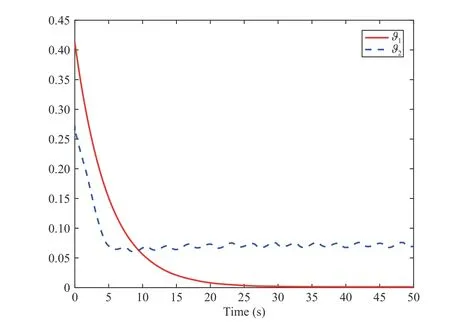
Fig.5. Trajectory of ϑ 1 and ϑ2 in Case 1.

Fig.6. State x1 tracking and tracking error in Case 2. (a) Trajectory of x1,yd and constraint interval; (b) Trajectory of tracking error.

Fig.7. Observation and error of state x1 in Case 2. (a) Trajectory of x1 , and constraint interval; (b) Trajectory of estimation errors .

Fig.8. Observation and error of state x2 in Case 2. (a) Trajectory of x2 , and constraint interval; (b) Trajectory of estimation errors

Fig.9. Trajectory of system input u in Case 2.
The above simulation results suggest that the adaptive output feedback control algorithm put forward in this paper can guarantee that all signals in the closed-loop system are bounded. Moreover, the full state constraints will never be violated, as well as the tracking performance of the system output is good.

Fig.10. Trajectory of ϑ 1 and ϑ 2 in Case 2.
V. CONCLUSIONS
For the full-state constrained nonlinear system with unknown states, the controller and adaptive laws are designed in this paper. Unknown and continuous functions are approximated by effective approximator fuzzy logic systems,where the fuzzy adaptive observer is constructed to dispose of immeasurable states. The backstepping technique is applied in the whole design process of controller. At the same time,iBLF is used to directly constrain the states, which solves the problem of conservative feasibility conditions and prevents constraints from being violated. Further, good tracking performance is guaranteed. What is more, tracking error,observation error, controller and adaptive law all fluctuate in a small range. All signals in the closed-loop systems are bounded. Last but not least, a simulation example verifies the effectiveness of the aforementioned forward control method.In future works, determining how to select an appropriate barrier Lyapunov function and design a fuzzy observer is a key problem for a practical system.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Ground-0 Axioms vs. First Principles and Second Law: From the Geometry of Light and Logic of Photon to Mind-Light-Matter Unity-AI&QI
- Deep Learning for EMG-based Human-Machine Interaction: A Review
- Distributed Secondary Control of AC Microgrids With External Disturbances and Directed Communication Topologies: A Full-Order Sliding-Mode Approach
- Deep Learning in Sheet Metal Bending With a Novel Theory-Guided Deep Neural Network
- Autonomous Control Strategy of a Swarm System Under Attack Based on Projected View and Light Transmittance
- Computing Paradigms in Emerging Vehicular Environments: A Review
