布站方式对基于TDOA的干扰源定位影响分析

2021-04-16胡人丹

导航定位与授时 2021年2期

胡人丹，常青

(北京航空航天大学电子信息工程学院，北京 100083)

0 引言

随着无线电技术的发展，电子信息战是当代社会战争的重要组成部分，如何识别和定位各种干扰成为了影响战局的关键性因素[1]。定位通常分为有源定位和无源定位，有源定位是指系统自身发射信号，并通过信号的反射实现定位的方式；无源定位是在不发射电磁波的情况下，通过接收干扰源发射的信号实现定位的方式。无源定位技术与有源定位相比，拥有良好的隐蔽性，以及较强的战场生存能力。

常用的无源定位技术有基于交叉测角(Angle of Arrival，AOA)的定位技术、基于到达时间(Time of Arrival，TOA)的定位技术[2]、基于到达频率差(Frequency Difference of Arrival，FDOA)的定位技术[3]和基于信号到达时间差(Time Difference of Arrival，TDOA)的定位技术[4-5]。TDOA定位技术基于辐射源信号到达各接收站的时间差，一般需要多个接收站测量同一个辐射源信号的到达时间。通过信号到达的时间差可以计算出距离差，当距离差为一个常数时，辐射源与接收站之间的位置关系就满足一个双曲线(面)方程[6]。在二维平面中，至少需要3个接收站才能计算出2个时间差，2个时间差就能得到2条双曲线，而双曲线的交点就是辐射源的位置。在三维空间中，至少需要4个接收站才能对干扰源进行定位。双曲线定位方法是一种较为精确的定位方法[7]，但也存在一些缺点，如当2条双曲线的交点不止一个时，就出现了模糊解问题。

在TDOA定位方式中，布站方式对模糊解区域的分布以及定位精度的影响很大[8]。在二维平面中，接收站之间的基线长度和接收站之间的角度对模糊区域分布具有较大影响。在三维立体空间中，接收机布站的形状和基线长度对几何精度因子(Geometric Dilution of Precision，GDOP)也有较大影响[9]。

本文针对TDOA定位方法中的布站问题，在二维平面对模糊区域进行仿真，得到了模糊解区域分布与接收站布站之间的关系。通过公式推导可以得出接收站的布站方式对TDOA系统的定位精度有较大的影响。为了定量分析不同的布站情况对TDOA定位精度的影响，本文对四站三维接收站进行了不同形状的布站并进行了仿真验证。仿真结果对实际工程应用中的TDOA布站有较强的借鉴意义。

1 TDOA定位原理

1.1 TDOA定位算法

多站时差定位算法要在空间中对辐射源进行定位，至少需要3个方程形成3个双曲面，这就至少需要4个接收站同步完成辐射源信号TDOA的测量，定位原理如图1所示。4个接收站中包括1个主站和3个辅站。

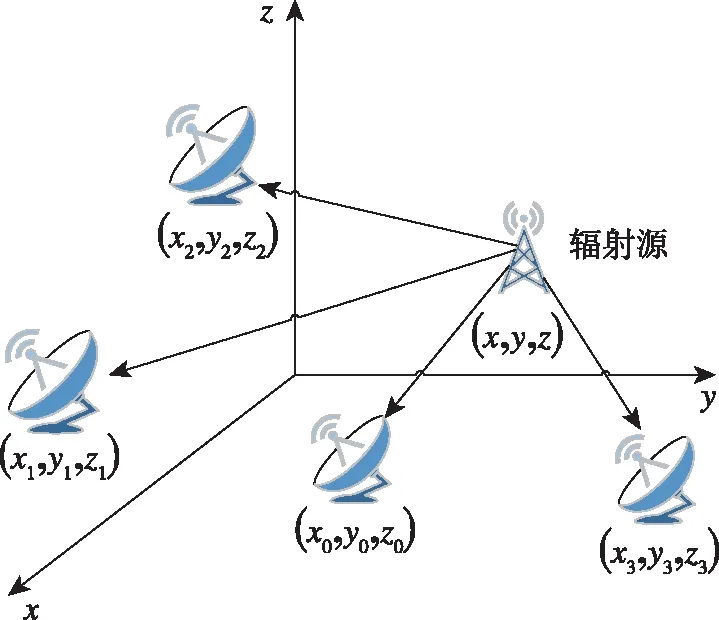
图1 基于TDOA的无源定位系统示意图Fig.1 Schematic diagram of passive location system based on TDOA

设待定的目标位置为(x,y,z)T，主站坐标为 (x0,y0,z0)T，辅站坐标为(xi,yi,zi)T(i=1,2,3)，r0表示目标到主站的距离，ri表示目标到各测量辅站的距离。目标到主站距离与到辅站距离的距离差为Δri，那么可得定位方程

(1)

式中，c为电波传播速度；Δti为目标信号到达第i个辅站与到达主站之间的时间差测量值；cΔti为第i个辅站到主站的距离差测量值。式(1)为一组关于目标辐射源位置坐标(x,y,z)的非线性方程组，目前有很多文献研究了关于这个方程组的解法，如Chan氏算法[10]、泰勒级数展开法[11]、球面相交法[12]和去距离最小二乘法[13]等。其中Chan氏算法是求解双曲线方程组的一种具有解析表达式解的非递归算法，该算法的特点是计算量小，无需做迭代运算，并可得到较好的定位结果。

1.2 Chan氏算法定位模型

利用Chan氏算法对式(1)整理化简可得

(x0-xi)x+(y0-yi)y+(z0-zi)z=ki+r0Δri

(2)

其中

(3)

为求解这个方程组式，可先将r0看作一个已知量，因此可得如下矩阵表达式

AX=F

(4)

其中

(5)

X=[xyz]T

(6)

(7)

在合适的布置接收站的位置条件下，即主站与任意2个辅站不在一条直线上时,rank(A)=3，用伪逆法求解方程(4)，可以得到

(8)

令

(9)

由式(8)可得

(10)

其中

(11)

在这里为了方便计算，假设x0=y0=z0=0，即参考主站的坐标在原点。此时式(4)中的

(12)

(13)

其中

(14)

此时x、y、z的解为

(15)

其中

(16)

因为主站在坐标原点，因此可以得到

(17)

将式(15)代入式(17)得

(18)

其中

(19)

由式(18)可解得r0的2个根

(20)

将r0代入式(1)，即可得到目标点的坐标(x,y,z)。

2 GDOP定位精度分析

2.1 GDOP定位精度模型

对Δri=ri-r0两边同时取微分

dΔri=(Hix-H0x)dx+(Hiy-H0y)dy+

(Hiz-H0z)dz+(ki-k0), (i=1,2,3)

(21)

其中

(22)

ki=Hixdxi+Hiydyi+Hizdzi, (i=0,1,2,3)

(23)

写成矢量形式为

dΔR=HdR+dS

(24)

其中主站与各辅站TDOA测量引入的误差为

dΔR=[dΔr1dΔr2dΔr3]T

(25)

欲求的目标定位误差为

dR=[dxdydz]T

(26)

各站站址引入的测量误差为

dS=[k1-k0k2-k0k3-k0]T

(27)

其中

(28)

由式(28)可得定位误差估计值的最小二乘解

(29)

由式(29)可知,目标定位误差(dxdydz)T与时差测量误差dΔR、站址测量误差dS及目标相对各站位置有关。由于各时间差测量信息中都包含有主站测量信息，即各时间差误差中都包含有共同的误差因素，因此各Δri的测量误差是相关的[14]。设Δri测量误差经系统修正后是零均值的，而站址误差在每次测量中是保持不变的，且站址误差各元素之间及各站址误差间互不相关，则定位误差协方差为

Pdr=E[dRdRT]

=C{E[dΔRdΔRT]+E[dSdST]}CT

(30)

式中

C=(HTH)-1HT=[cij]3×3

(31)

E[dΔRdΔRT]=

(32)

E[dSdST]=

(33)

其中，σΔri为第i个辅站与主站之间的测量误差标准差;ηij表示Δri与Δrj之间的相关系数

(34)

σxi、σyi、σzi为各站址测量误差分量的标准差。假设各站址测量误差标准差相同，即

(35)

又因为

(36)

可得

(37)

令

[eij]3×3=E[dΔrdΔrT]+E[dSdST]

(38)

[eij]3×3=

(39)

[eij]3×3=

(40)

由此可得定位误差在x、y、z上的方差分别为

(41)

则

(42)

2.2 定位无解区与定位模糊区原因分析

对关于r0的一元二次方程ar02+br0+c=0进行求解，可以得到r0的数值解。根据一元二次方程的特点，可以从解的情来进行分析[15]。

1)Δ=b2-4ac<0时，方程的解为2个虚数，方程无实数解，无法准确定位。

2)Δ=b2-4ac=0时，方程有唯一解，能够准确定位且定位结果唯一。

3)Δ=b2-4ac>0时，方程有2个解r01和r02，此时又可以分为以下两种情况：

(1)r01r02<0，取r01和r02中正值为定位结果；

(2)r01r02>0，若r01和r02都为正，则此时出现了定位模糊，需要借助一定手段来消除定位模糊。

在实际系统中，由于噪声干扰、多路径传输和信道环境恶劣等原因导致的时差测量误差不可避免。时差测量误差使原本相交的双曲线出现偏移，进而导致出现无解情况。

3 仿真验证

3.1 平面三站系统模糊度仿真

如图2所示，以主站S0为坐标原点建立坐标系，辅站S1到主站S0之间的距离为L1，辅站S2到主站S0之间的距离为L2。L1与L2之间的夹角为θ，L1和L2的长度为基线长度。

对图2所示的时差定位系统在不同布站形式下的模糊度进行仿真，分别将夹角设置为60°、90°和120°，同时改变基线长度，设置坐标如表1所示。仿真假设X、Y坐标范围均为[-200,200]，单位为km，仿真结果如图3～图8所示。

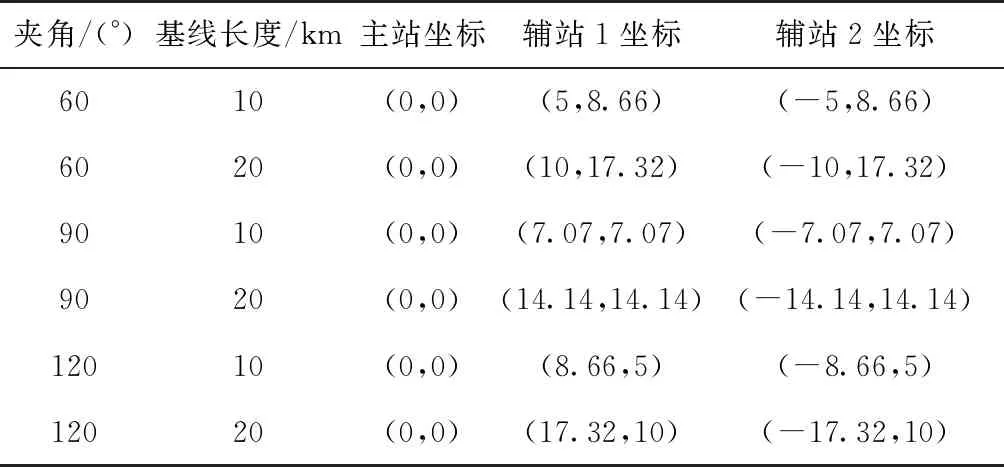
表1 不同条件下接收站位置坐标

图3和图4为夹角60°时基线长度分别为10km和20km布站条件下的模糊区域分布情况；图5和图6为夹角90°时基线长度分别为10km和20km布站条件下的模糊区域分布情况；图7和图8为夹角120°时基线长度分别为10km和20km布站条件下的模糊区域分布情况，图中蓝色的点为定位模糊点。通过对比图3和图4可以得到，基线长度增加，模糊区域减小；通过对比图3、图5和图7可

以得到，模糊区域主要分布在基线延长线及其夹角区域。接收站辅站与主站形成的夹角增大，则主站上方的无模糊区域增加，主站下方延长线形成的模糊区域也增加。

图3 夹角为60°基线长度为10km的模糊区Fig.3 Fuzzy area with the included angle of 60 degrees and the baseline length of 10km

图4 夹角为60°基线长度为20km的模糊区Fig.4 Fuzzy area with the included angle of 60 degrees and the baseline length of 20km

图5 夹角为90°基线长度为10km的模糊区Fig.5 Fuzzy area with the included angle of 90 degrees and the baseline length of 10km

图6 夹角为90°基线长度为20km的模糊区Fig.6 Fuzzy area with the included angle of 90 degrees and the baseline length of 20km

图7 夹角为120°基线长度为10km的模糊区Fig.7 Fuzzy area with the included angle of 120 degrees and the baseline length of 10km

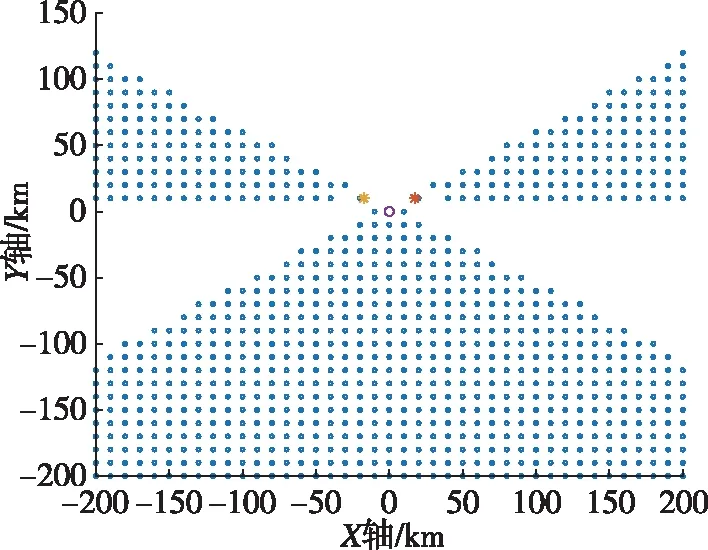
图8 夹角为120°基线长度为20km的模糊区Fig.8 Fuzzy area with the included angle of 120 degrees and the baseline length of 20km

3.2 四站三维系统精度仿真

决定定位精度大小的因素包括：站址测量误差标准差、各接收站与目标辐射源的几何位置、接收站的布站方式和时差测量误差标准差等。其中对定位精度影响最大的因素是各接收站与目标辐射源之间的几何位置关系[16]。通过观察GDOP的表达式可以看出，GDOP的物理意义为3个坐标轴方向上的测量误差，因此GDOP越小，误差越小，测量精度越高。下面对三种最常见的布站方式进行GDOP仿真，这三种布站方式分别是：菱形、Y形和T形。各站坐标如表2所示。

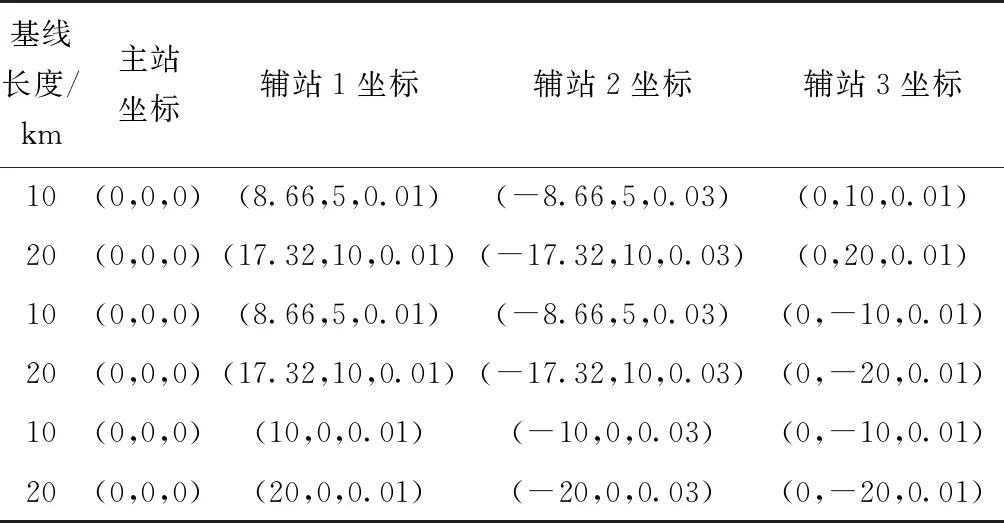
表2 不同形状下接收站位置坐标

仿真假设X、Y坐标范围均为[-300,300]，单位为km，时差测量精度固定为10ns，仿真结果如图9～图14所示。

图9 基线长度为10km菱形布站下的GDOP分布Fig.9 The GDOP distribution under the rhombus station with a baseline length of 10km

图10 基线长度为20km菱形布站的GDOP分布Fig.10 The GDOP distribution under the rhombus station with a baseline length of 20km

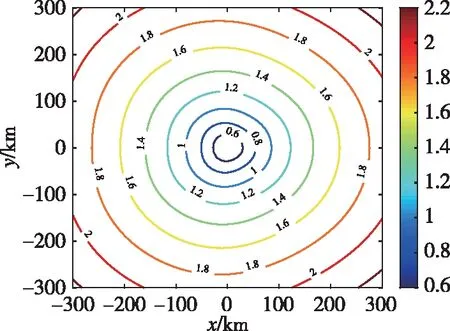
图11 基线长度为10km Y形布站的GDOP分布Fig.11 The GDOP distribution with a baseline length of 10km Y shaped station

图12 基线长度为20km Y形布站的GDOP分布Fig.12 The GDOP distribution with a baseline length of 20km Y shaped station

图13 基线长度为10km T形布站的GDOP分布Fig.13 The GDOP distribution with a baseline length of 10km T shaped station

图14 基线长度为20km T形布站的GDOP分布Fig.14 The GDOP distribution with a baseline length of 20km T shaped station

图9和图10分别为基线长度为10km和20km时菱形布站下的GDOP分布，通过观察可以得到：基线长度越长，在相同坐标点的GDOP越小，定位精度越高。图11和图12分别为基线长度为10km和20km时Y形布站下的GDOP分布，图13和图14分别为基线长度为10km和20km时T形布站下的GDOP分布，通过对比图9、图11和图12可知，在相同基线长度下，Y形布站各个方向的GDOP分布较为均匀；菱形布站在对角线连线区域定位精度较高，在基线延长线方向定位精度较低；T形布站在三站在同一条延长线方向上的定位精度较高，在其垂直方向定位精度较低。