饮用水中铜绿假单胞菌检测结果的 不确定度评定

◎ 田 浩，李光耀，张 凡，王 杰，史笑娜，马骁杰，杨少淼

（1.河北东淼检测科技股份有限公司，河北 保定 071000；2.河北纳微环境检测有限公司，河北 保定 071000）

2015 年5 月实施的《食品安全国家标准 包装饮用水》（GB 19298—2014）中增加了铜绿假单胞菌（Pseudomonas aeruginosa）限量，而不再使用传统的菌落总数指标对包装饮用水的卫生情况进行评价。根据国内外的研究情况，Nagaveni 等在匈牙利国内492 份成品水中的7 份检出铜绿假单胞菌，该菌的污染率为1.4%[1]；魏磊等在中国9 个省36 家水厂采集的108 个包装饮用水样品中铜绿假单胞菌的污染率达到了5.6%[2]。

铜绿假单胞菌分布广泛，对有机营养要求较低，对不良环境抵抗力强，世界卫生组织（WHO）将其列为人类皮肤污染指示菌；HACCP（Hazard Analysis Critical Control Point）评估明确指出其是婴儿瓶装饮用水的危害指示菌，可造成婴儿腹泻[3]。由此可知，生活饮用水中的铜绿假单胞菌是一种污染率较高、危害较为严重的卫生指示菌。

《检测和校准实验室能力的通用要求》（ISO/IEC17025：2005）明确要求认可实验室需评定和报告测量不确定度[4]；《测量不确定度的要求》（CNAS-CL07：2011）中明确要求“实验室应有能力对每一项有数值要求的测量结果进行测量不确定度评定”[5]；CMA（China Metrology Accreditation）评审依据的《检验检测机构资质认定评审准则》明确要求“检验检测机构应根据需要建立和保持应用评定测量不确定度的程序”[6]。近年来，食品检测领域的第三方实验室发展加速，不确定度评定作为保证数据质量、规范检测行为的重要手段逐渐受到各方的重视。在实践中，微生物检测数据出现临界值、不符值等非正常值时，正确评定不确定度可以保证检测结果的科学性和公正性[7]。但由于生物学科本身分散性较强和不易度量的特点，不确定度评定的应用仍主要存在于非生物类实验中。

为探索有效、简便、适用的微生物实验不确定度评定方案，本研究针对包装饮用水中铜绿假单胞菌检测结果的不确定度进行评定。首先分析不确定度产生来源并分别计算不同分量产生的不确定度，而后得出合成不确定度和扩展不确定度，最后折算回检测结果，得到报告范围。

1 材料与方法

1.1 材料

参照《食品安全国家标准 食品微生物学检验 培养基和试剂的质量要求》（GB 4789.28—2013）附录D 要求采用标准菌株ATCC 27853 铜绿假单胞菌，自中国工业微生物菌种保藏管理中心购买[8]。本研究采用三代生长期标准菌株。

包装饮用水样品（批号：20170325），自保定市场采购买。使用1.1 中的标准菌株对包装饮用水样品进行人工污染。

1.2 仪器与试剂

3M Petrifilm 致病菌测试纸（环凯微生物科技有限公司）、灭菌精密250 mL 玻璃量筒（易购安（北京）科技有限公司）、0.1 ℃ ZHSY恒温培养箱（三洋电机（中国）有限公司）、ZF-20C 紫外灯（上海楚柏实验室设备有限公司）、0.45 μm 无菌滤膜（杭州盈天科学仪器有限公司）、100×显微镜（株式会社日立制作所）、BCD-610W 冰箱（罗伯特·博世有限公司）以及BHC-1300IIA/B2生物安全柜（苏州净化设备有限公司）。

假单胞菌琼脂基础培养基/CN 琼脂（编号：20170112F）、金氏B（King’s B）培养基（编号：20170112）、乙酰胺液体培养基（编号：20170119）、绿脓菌素测定用培养基（编号：160919）、营养琼脂（编号：20160115）、氧化酶试剂（编号：20160824）以及钠氏试剂（编号：20170112）。

1.3 方法

按照《食品安全国家标准 饮用天然矿泉水检验方法》（GB 8538—2016）中铜绿假单胞菌[9]的要求进行检测，得到原始数据。量取250 mL 水样，0.45 μm无菌滤膜过滤，将滤膜移至CN 琼脂培养基上，于（36±1）℃恒温培养箱中培养48 h；可疑菌落分别计数并进行确证性实验，确证标准见表1。

表1 确证性实验表

最后进行结果报告，计算每250 mL 水样中的铜绿假单胞菌数量，结果以CFU/250 mL 计。结果按式（1）进行计算：

式（1）中，P-呈蓝/绿色的菌落数；F-显荧光的菌落数；cF-产氨阳性的显荧光菌落数；nF-进行产氨测试的显荧光菌落数；R-呈红褐色的菌落数；cR-产氨、氧化酶、金氏B 培养基上显荧光测试均呈阳性的红褐色菌落数；nR-进行产氨、氧化酶、金氏B 培养基上显荧光测试的红褐色菌落数。

1.4 统计学处理

设水样中铜绿假单胞菌检测结果为T，检测结果为X，则T=XCFU/250 mL。

1.4.1 不确定度的来源

和一般测量相比较，样品中微生物测量的结果特点是发散性极大[10]。在微生物检验中，样品重复测量带来的不确定度是影响检验结果准确度的主要原因[11]。除此之外，微生物分布、环境条件、样品称量、成品培养基批次、样品过滤和人员因素均能导致不确定度，其中能够直接影响检测准确度并可以进行不确定度评价的为样品称量方面和样品重复测量方面，重复测量带来的不确定度占主要部分。

1.4.2 不确定度的评定方法

根据对铜绿假单胞菌检测过程中不确定度的来源进行的分析，同时结合微生物检测的学科特点，本研究采用B 类不确定度的统计方法评定样品称量环节产生的不确定度，采用A 类不确定度的统计方法来评定样品重复测量环节产生的不确定度。

本研究采用人工污染样品的方式来模拟实际样品的检测，从而获得足够的检测数据。实际的检测结果呈现偏态分布、分散性强、不易评定的特点，故首先采用指数法对原始数据进行处理，使处理后的数值符合正态分布，从而评定铜绿假单胞菌检测结果的不确定度。

2 结果与分析

2.1 样品称量过程中产生的不确定度

使用250 mL 无菌玻璃量筒，精度0.1 mL，根据《常用玻璃量器检定规程》（JJG 196—2006）规定，量出式250 mL 量筒的容量允差为±2.0 mL，称量误差服从矩形分布，包含因子kp=[12]。

样品称量引入的不确定度ur为：

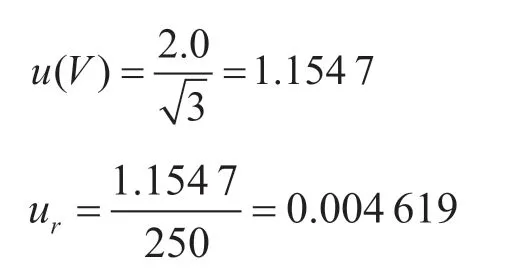
2.2 样品重复检测产生的不确定度

在相同条件下，同一名检测人员对同一包装饮用水样品进行重复检测30 次，得检测结果Xi。检测结果见表2。

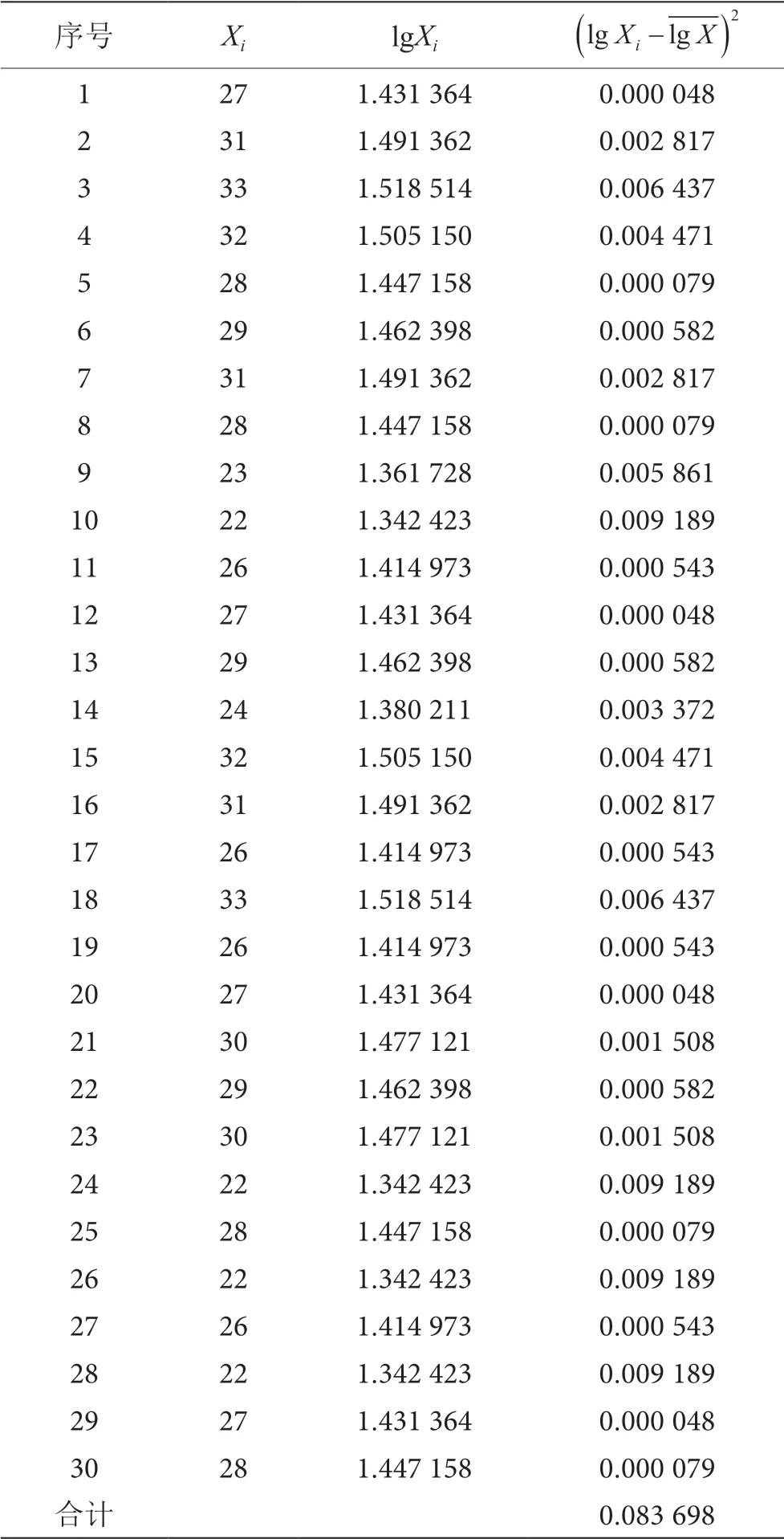
表2 检测结果表

得到检测结果的原始数据（Xi）后，将Xi取对数得lgXi，计算得对数值的平均值，再利用贝塞尔公式计算每组数据的标准偏差的平方得计算合并标准偏差得s，最后得样品重复检测合成标准不确定度uc。

合并样本标准偏差：

样品重复检测合成标准不确定度：

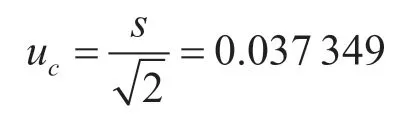
2.3 合成不确定度

将不同来源的不确定度进行合成，得包装饮用水中铜绿假单胞菌检测结果的合成不确定度u。

2.4 扩展不确定度

取置信区间P=95%，自由度v=30-1=29，查询t分布表得包含因子k95（29）=2.05，可得包装饮用水中铜绿假单胞菌检测结果的扩展不确定度U。

2.5 报告范围

根据得到的扩展不确定度U，得到lgX的取值范围；将lgX取反对数折算为检测结果X，得到X的取值范围，从而得到包装饮用水中铜绿假单胞菌的检测结果T的报告范围：

该包装饮用水中铜绿假单胞菌的检测结果为T=23 ～33 CFU/250 mL。

3 结论与讨论

2017 年6 月实施的《食品安全国家标准 食品微生物学检验 总则》（GB 4789.1—2016）明确要求“检验结果报告后，剩余样品和同批产品不进行微生物项目的复检”[13]。微生物项目不得复检的特点决定了对其检测数据的准确性有更严格的质量要求，也对其不确定度评价方案的建立提出了更高的要求。

不确定度评价可以定量反映检测结果的质量好坏，本研究计算得到的报出范围与样品的实际检测结果较为一致，但是不确定度的评定过程步骤仍然较为繁琐和不便，中间过程采用了指数法等统计方法，主要原因在于微生物实验的原始数据普遍呈现偏态分布，缺少固定规律、可变性强、重复性差；这也是微生物检测项目不易建立规范的不确定度评价方案的难点所在。只有在检测结果＜10 CFU·mL-1的情况下，其才能接近于正态分布，不需要进行对数转换[14]。本研究采用的为液体样品且无需进行稀释，如遇其他检测项目需均质、稀释等过程，不确定度也会随之变化。

不确定度评价方案的建立首先要分析不确定度产生的来源，微生物实验有自动化仪器少、人员参与多、检测周期长和结果统计主观性强的特点，由此导致不确定度产生的来源较多，主要有样品重复检测、样品称量或吸取、无菌室环境（风力、温度、湿度等）、样品种类变化、培养基批次变化、样品均一性及微生物动态变化等，其中培养基批次变化、微生物动态变化等一些微生物实验特有的不确定度产生来源尚未有完善的测量法或统计学的评定方法。这些因素造成的不确定度，需要依靠引进自动化仪器、严格质量控制（实验室比对、能力验证、质量考核等方式）手段来进行减少或评定。

在可评定的因素中，样品重复检测已经确定为微生物实验中的首要不确定度来源，在本研究中其带来的不确定度为样品称量来源的8.1 倍左右。如假设其他因素均可忽略的话，样品重复检测带来的不确定度占到全部不确定度的89%左右。目前，我国食品微生物检测项目逐渐开始使用2 级或3 级的高级别采样方案（n≥5）进行样品检测，本文也为其提供了理论依据。而样品称量过程中带来的不确定度，需要依靠使用优良计量器具、开展器具比对、开展人员比对等方式进行减少。

在实践中，微生物实验进行不确定度评定的意义主要在于当出现要求限值附近的检测结果时，利用扩展不确定度对样品进行符合性判定。在95%置信概率下，当检验结果延伸扩展不确定度半宽度后仍小于（大于）限量标准时。当检验结果低于（高于）限量标准的部分小于测量不确定度，则在95%置信概率上不能做出符合（不符合）限量标准的声明[15]。