Computation of an Emptiable Minimal Siphon in a Subclass of Petri Nets Using Mixed-Integer Programming

Shouguang Wang, Senior Member, IEEE, Wenli Duo, Xin Guo, Xiaoning Jiang,Dan You, Kamel Barkaoui, and MengChu Zhou, Fellow, IEEE

Abstract—Deadlock resolution strategies based on siphon control are widely investigated. Their computational efficiency largely depends on siphon computation. Mixed-integer programming (MIP) can be utilized for the computation of an emptiable siphon in a Petri net (PN). Based on it, deadlock resolution strategies can be designed without requiring complete siphon enumeration that has exponential complexity. Due to this reason, various MIP methods are proposed for various subclasses of PNs. This work proposes an innovative MIP method to compute an emptiable minimal siphon (EMS) for a subclass of PNs named S4PR. In particular, many particular structural characteristics of EMS in S4PR are formalized as constraints,which greatly reduces the solution space. Experimental results show that the proposed MIP method has higher computational efficiency. Furthermore, the proposed method allows one to determine the liveness of an ordinary S4PR.

I. INTRODUCTION

PETRI nets (PNs) are an extensively used tool of mathematics for dealing with the presence of deadlock states in various discrete event systems, such as workflow systems [1]-[3], business systems, railway networks [4] and flexible manufacturing systems [5], [6]. A siphon is a structural object of PNs. Its token count is closely associated with the presence of deadlocks [7]. For example, a deadlock may arise in ordinary PNs when there is a siphon being emptied, i.e., when its token count is zero. Consequently,many deadlock resolution strategies [8]-[24] are developed based on siphon control. They all require a step called siphon computation. It in turn decides the computational complexity of such deadlock resolution strategies. Due to this reason,researchers study the ways to perform efficient siphon computation.

Many studies focus on the complete enumeration of siphons in a PN. Some methods can be utilized for general nets, such as problem partitioning methods [25], [26], graph theory [27],[28], sign matrix methods [29], genetic algorithms [30], [31],binary decision diagrams [32] and INA-based methods [33].The other ones are proposed for specific subclasses of PNs[16], [34]-[39] which have higher computational efficiency than methods applicable to general nets. These proposed methods have greatly improved the computational efficiency of complete siphon enumeration. However, they are of exponential complexity with respect to the net size. This is because at worst, the number of siphons in a PN grows exponentially in terms of the net size. Therefore, deadlock resolution strategies calling for complete siphon enumeration have high computational complexity.

Can we find deadlock control strategies with no complete siphon enumeration? Chu and Xie [40] introduce a mixedinteger programming (MIP) method for detecting the existence of deadlocks in PNs. In more detail, they propose an MIP problem where one maximal emptied siphon is derived if its solution is found. More significantly, no siphon is emptiable in the case no solution is found. This important result can thus be utilized to determine the deadlock-freedom or liveness of a PN. The MIP method is computationally efficient even when applied to large-scale nets since it does not require the reachability analysis and thus avoids the problem of state explosion. Based on it, Huang et al. [41]develop a liveness-enforcing policy in an iterative way for a subclass of PNs called “ systems of simple sequential processes with resources (S3PR)”. The basic idea is that, at every iteration, it uses an MIP method to compute a maximal emptied siphon, then extracts a minimal siphon from the obtained maximal emptied siphon, and finally makes the extracted minimal siphon controlled. Such a policy successfully avoids the complete enumeration of siphons and thereby has much higher computational efficiency than those requiring complete siphon enumeration. The minimal siphon extraction from a maximal emptiable siphon is also studied in[10] and [42]. In addition, after the work by Chu and Xie [40],a variety of revised MIP methods are proposed in the literature for the purpose of checking/ensuring liveness or deadlockfreedom of concerned subclasses of PNs, e.g., [43]-[46].

We observe that the constraints in the existing MIP formulations like those in [40] represent properties of siphons in general nets only. In other words, although some revised MIP methods are proposed for specific subclasses of PNs, the particular properties or structural characteristics of emptiable siphons in specific nets are not taken into consideration, which actually may contribute to lowering the computational time.For example, in our previous work [47], we propose an improved MIP method for S3PR to compute an emptiable minimal siphon (EMS), where the structural characteristics of EMS in S3PR are utilized to construct constraints. We can see that the more non-redundant constraints we add, the smaller the solution space is and thus the higher the computational efficiency is. Experimental results in [47] validate that the improved MIP method outperforms greatly the MIP method in[40] in terms of computational efficiency, which is more evident for large-size nets.

Inspired by the work [47], we seek to determine if such a strategy can be extended for a more general net than S3PR.This work addresses this issue by dealing with S4PR.Specifically, we propose a novel MIP method to compute an EMS in S4PR where the particular structural characteristics of EMS in such nets are formalized as constraints for the first time. Compared with the existing MIP formulations applicable to S4PR, the solution space of the proposed MIP problem is narrowed down since more non-redundant constraints are added. Experimental results in the paper show that the proposed method is of higher computational efficiency than existing ones in the literature.

We note that S4PR are generalized PNs, i.e., they may contain arcs whose weight is more than one. Thus, the absence of EMS in an S4PR is only a necessary condition to guarantee the deadlock-freedom of the S4PR [48]. However, it is clear to see that if there exists an EMS in an S4PR, it can be concluded that the S4PR suffers from deadlocks. In addition, given an S4PR that is ordinary, if there exists no EMS, it can be concluded that the net is not only deadlock-free but also live[45]. Consequently, the proposed MIP method, which can detect whether or not there exists an EMS in an S4PR, is capable of determining the liveness of ordinary S4PR and denying the deadlock-freedom for some generalized S4PR.Moreover, since the absence of EMS in an S4PR is a necessary condition for the net being deadlock-free, iterative deadlock control strategies for S4PR may be developed involving the computation and control of an EMS as an intermediate step. In other words, the proposed MIP method may be involved in developing iterative deadlock control strategies for S4PR.

The other sections of this paper are organized as follows.Section II reviews basic notions of Petri nets and S4PR.Section III shows the structural characteristics of EMS in S4PR. A new MIP method is proposed in Section IV to detect an EMS in S4PR and determine the liveness of an ordinary S4PR. In Section V, we compare the computational efficiency of the proposed MIP with others. Section VI concludes this paper.

II. PRELIMINARIES

A. Petri Nets

A P-vector is a column vector I: P →Z indexed by P. I is called a P-invariant if I ≠ 0 and IT·[N] = 0Thold. ||I|| = {p ∈ P|I(p) ≠ 0} is called the support of I. A P-invariant I is called a P-semiflow if every element of I is non-negative. A Psemiflow I is minimal if the greatest common divisor of its non-zero components is 1 and ||I|| is not a superset of the support of any other P-semiflow.

·S ⊆S·

A nonempty set S ⊆ P is a siphon if . A siphon is called minimal if it does not contain any other siphon. A minimal siphon that does not contain the support of any Psemiflow is called a strict minimal siphon (SMS). Given a marked Petri net (N, M0), an emptiable minimal siphon (EMS)is a minimal siphon in N that can be emptied (or unmarked) at a marking M ∈ R(N, M0).

Given a marked Petri net (N, M0), a transition t ∈ T is live at M0if ∀M ∈ R(N, M0), ∃M' ∈ R(N, M) such that t is enabled at M'. (N, M0) is live if ∀t ∈ T, t is live at M0.

B. S4PR

The S4PR studied in our paper is proposed by Tricas et al. in[48], [49], where they say that the name “S4PR” does not have any specific meaning.

Definition 1 [48], [49]: An S4PR is a generalized connected self-loop free Petri net N = (P, T, F, W), where

III. EMPTIABLE MINIMAL SIPHONS IN S4PR

In this section, we explore properties of EMS in S4PR,which can be utilized later to accelerate the computation of its EMS.

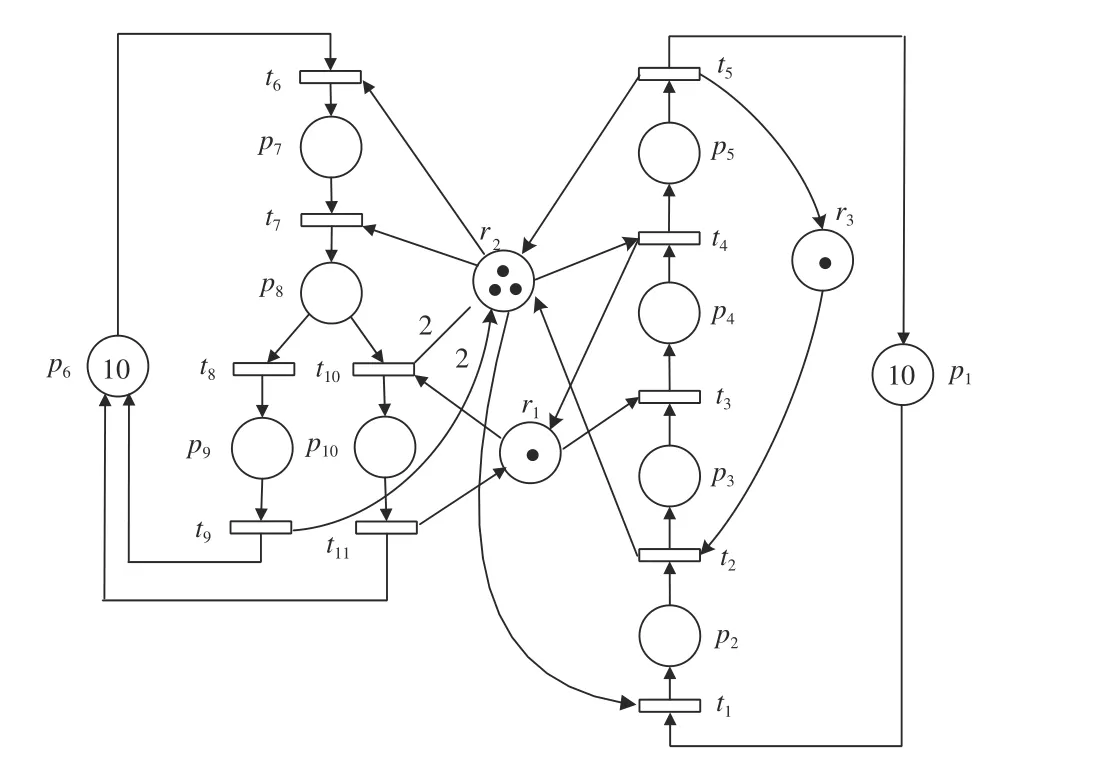
Fig. 1. A marked S4PR (N, M0).

In simple words, a pure activity path with respect to a resource subset Ω is an elementary path where each place is an activity place and none of transitions is connected with resources from Ω except the starting and ending ones.

Consider the S4PR N in Fig. 1. There is a resource subset Ω = {r1, r2}. π1= t7p8t8p9t9and π2= t6p7t7p8t8p9t9are clearly two elementary paths. By Definition 3, π1is a pure activity path in regard to Ω, while π2is not.

Definition 4 [50]: Given a resource subset Ω, a transition t∈ T and an activity place p ∈ PAin an S4PR, p is said to be a restoring place of t with respect to Ω if t is accessible from p via a pure activity path with respect to Ω. P+(t, Ω) denotes the set of all restoring places of t with respect to Ω.

Consider again the S4PR N in Fig. 1, a resource subset Ω ={r1, r2} and t9. It can be seen that t9is accessible from p9via a

Fig. 2. The IRT net of N in Fig. 1 induced by Ω = {r1, r2, r3}.

Proposition 3 [50]: Given an S4PR N and a resource subset Ω, the Ω-induced IRT net NΩis strongly connected if SΩis an SMS.

For simplicity, we use NRto denote a PR-induced IRT net,i.e., the IRT net induced by the set of all resource places of an S4PR.

Obviously, the IRT net induced by any resource subset Ω ⊆PRis a subnet of the PR-induced IRT net NR. Thus,straightforward from Proposition 3, we have the below result.

Proposition 4: Given an S4PR N, its PR-induced IRT net NR,and a place set S in N, if S is an SMS, then ∀r ∈ S ∩ PR, ∃r'∈ I(r) such that r' ∈ S and ∃r'' ∈ O(r) such that r'' ∈ S.

It is clear that any EMS in an S4PR is definitely an SMS.Hence, the structural characteristics of SMS in S4PR can be used to search EMS more efficiently. Following Propositions 2 and 4, we can see that if a place set S in an S4PR is an EMS,then 1) S consists of resource and activity places; and 2) ∀r ∈S ∩ PR, ∃r' ∈ I(r) such that r' ∈ S and ∃r'' ∈ O(r) such that r''∈ S.

IV. COMPUTATION OF EMS IN S4PR

In this section, we construct a new mixed-integer programming (MIP) problem to compute an EMS in S4PR.We introduce a binary variable vp∈ {0, 1} for each place p to indicate whether p is contained in a siphon. Specifically, vp=1 indicates p ∈ S and otherwise not, where S is a siphon.Then, we can compute an EMS in S4PR by solving the following MIP problem, denoted as MIP*.

MIP*:

Theorem 1: Given S4PR (N, M0) and M ∈ R(N, M0), a solution to (1)-(11), if it exists, corresponds to an EMS.

Proof: Let S be a set of places that corresponds to a solution to (1)-(11). By Proposition 8, S is a minimal siphon. Because of (11), it is clear that S is emptied at M. Since M ∈ R(N, M0),S is an EMS. ■

Theorem 2: Given S4PR (N, M0) and M ∈ R(N, M0), there is a solution to (1)-(11) if there is an EMS that can be emptied at M.

Proof: Let S be the EMS that can be emptied at M. By Proposition 5, S corresponds to a solution to constraints (2)-(10). Since S is emptied at M, S corresponds to a solution to constraint (11). Hence, the solution space meeting constraints(2)-(11) is not empty. Clearly, there is a solution to the objective function (1) and constraints (2)-(11). ■

Theorem 3: Given an S4PR (N, M0), if a solution to MIP*exists, then it corresponds to a minimal siphon in N that can be emptied at a marking M where M = M0+ [N]Y, M ≥ 0, Y ≥ 0.

Proof: Let S be a set of places that corresponds to a solution to MIP*. By Proposition 8, S is a minimal siphon. Because of(11) and (12), it is trivial to see that S is a minimal siphon that is emptiable at M = M0+ [N]Y, M ≥ 0, Y ≥ 0. ■

Remark 1: We should point out that a solution to MIP* is not necessarily an EMS in S4PR. This is because we use the state equation (12) to restrict the marking space searched in MIP*, which, however, is not exactly the reachable marking set R(N, M0). To be more precise, R(N, M0) is only a subset of the marking set described by (12). Consequently, it could happen that the solution to MIP* corresponds to a minimal siphon that is emptied at some markings satisfying (12) but none of them is reachable in a given S4PR. Such a minimal siphon is clearly not an EMS. ■

Based on the solution for MIP*, we propose a sufficient condition under which an ordinary S4PR is live.

Theorem 4: Given an ordinary S4PR (N, M0), it is live if its MIP* has no solution.

Proof: According to Proposition 6, there exists no EMS in(N, M0). It is proved in [45] that an ordinary S4PR is live if there is no EMS. Hence, (N, M0) is live. ■

Remark 2: This work is a generalization of our previous work [47]. Specifically, an improved MIP for computing an EMS is proposed in [47] that is applicable to S3PR only, while in this work we propose MIP* that is applicable to S4PR.Since S4PR is a more general class of PNs than S3PR, MIP* is thereby also applicable to S3PR to compute an EMS. Actually,both the improved MIP in [47] and MIP* in this work are inspired by the idea of formulating the structural characteristics of EMS as constraints to narrow down the solution space. Due to the fact that the structural characteristics of EMS in S4PR are much more complex than those in S3PR, MIP* is more complex than the improved MIP in [47] in terms of constraints.

V. COMPARISON ON COMPUTATIONAL EFFICIENCY

In this section, we perform a computation experiment to compare the computational efficiency of the proposed MIP method (MIP*) and the MIP method in [40]. The computation is conducted on a 3.20 GHz Intel Core i5 computer with 6 GBRAM memory, and the software “Lingo12.0” is used as a tool to solve MIP problems.

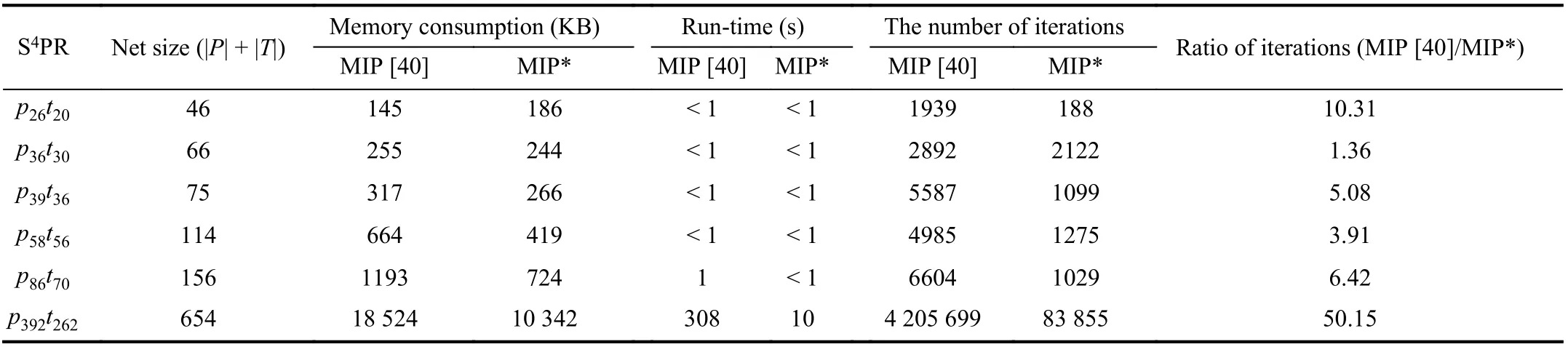
TABLE I EXPERIMENTAL RESULTS OF MIP [40] AND MIP*

In the experiment, six S4PR named p26t20, p36t30, p39t36,p58t56, p86t70, p392t262are considered, whose net sizes vary from 46 nodes to 654 nodes. Note that their concrete models are presented in [51] for the sake of saving space. Indeed, the first five nets are classical examples studied in the literature,while the sixth net is the largest net among them constructed in our previous work [47]. By applying MIP* and the MIP in[40] to them to compute an EMS, the required memory consumption, run-time and the number of iterations are exhibited in Table I. We can see that, with the increase of the net size, it is clear that MIP* consumes less computer memory and enjoys higher computational efficiency than the MIP in[40].

VI. CONCLUSIONS AND FUTURE WORK

This work proposes a novel MIP method to compute an EMS in S4PR. It innovatively explores and utilizes the structural characteristics of EMS in it to construct new constraints for its MIP formulation. In particular, the structural characteristics of SMS in S4PR are formalized as constraints since an EMS in S4PR is proved to be an SMS. In comparison with the existing MIP methods, we conclude that the new one has higher computational efficiency since its solution space is reduced. Furthermore, based on the proposed MIP method, we establish a sufficient condition for an ordinary S4PR to be live.Our future work includes: 1) Developing liveness-enforcing supervisors for S4PR based on the proposed MIP method; and 2) Extending the presented method to more generalized classes of Petri nets modeling various discrete event systems[52]-[62].