Finite-Time Convergence Disturbance Rejection Control for a Flexible Timoshenko Manipulator
2021-04-14ZhijiaZhaoMemberIEEEandZhijieLiuMemberIEEE
Zhijia Zhao, Member, IEEE and Zhijie Liu, Member, IEEE
Abstract—This paper focuses on a new finite-time convergence disturbance rejection control scheme design for a flexible Timoshenko manipulator subject to extraneous disturbances. To suppress the shear deformation and elastic oscillation, position the manipulator in a desired angle, and ensure the finitetime convergence of disturbances, we develop three disturbance observers (DOs) and boundary controllers. Under the derived DOs-based control schemes, the controlled system is guaranteed to be uniformly bounded stable and disturbance estimation errors converge to zero in a finite time. In the end, numerical simulations are established by finite difference methods to demonstrate the effectiveness of the devised scheme by selecting appropriate parameters.
I. INTRODUCTION
MANIPULATORS are generally applied in a variety of different fields, such as industry, national defense,agriculture, and healthcare [1]-[3]. Flexible manipulators described by partial differential equations (PDEs) have recently received more attention than rigid ones modelled as ordinary differential equations (ODEs) due to their advantages of lower energy consumption, light weight, large operating space, and high-speed operation [4], [5]. Facing the complex and various environments, vibration and deformation generally exist in flexible manipulators, giving rise to system performance deterioration or even production accuracy decline [6]. Thus, the development of efficient control methods for suppressing the oscillation in flexible manipulators is of great interest.
To dampen vibration and improve performance of flexible manipulator systems, several researchers have concentrated on exploring diverse control techniques, such as mode order reduction (MOR) method [7]-[9] and boundary control [10].By applying the MOR method, an infinite-dimensional system is turned into a finite-dimensional system [11]-[13]. It may weaken the characteristics and cause spillover effects, thus affecting the stability and robustness of the system. Boundary control has been perceived as an effective and practical solution, owing to the circumvention of the spillover effect generated from the MOR method [14]-[20]. Over the past 20 years, advances in the study of boundary controller design for weakening the vibrational offset of flexible manipulators have been significantly made. For example, in [10], disturbance observers (DOs) and boundary controllers were constructed to stabilize the oscillation and eliminate the disturbances in flexible manipulators. In [21], the vibration and angle of flexible manipulators were restrained and positioned by devising a hyperbolic function-based boundary control law. In[22], the nonlinear coupled oscillation of a flexible manipulator in 3-dimensional (3D) space was weakened by exploiting boundary controllers. A boundary barrier-based control was employed for flexible manipulators to achieve the vibration abatement and ensure no violation of output constraints in [23]. In [24], vibration damping and angle positioning in flexible manipulators were accomplished by proposing an iterative learning control strategy. In [25],exploiting the developed boundary control and the Lyapunov stability theory, the angle positioning, vibration abatement,and closed-loop stability of two-link flexible manipulators were realized. In [26], flexible manipulator systems were globally stabilized by using boundary feedback control schemes, and an adaptive inverse technique was employed for tackling the backlash nonlinearity. In the aforementioned literatures, only the elastic oscillation of the flexible link was taken into account, and the shear deformation was neglected to simplify the system analysis. The nonlinear coupling of angle position, shear deformation, and elastic deflection may pose increased challenges for the design and analysis. In recent years, significant development of boundary control for flexible Timoshenko manipulators has been achieved in[27]-[30]. In [27], [28], cooperative control methodologies were devised to guarantee the exponential stabilization of flexible Timoshenko manipulators. In [29], an antisaturation boundary control was established for vibration elimination and saturation removing of Timoshenko manipulators. The literature of [30] constructed an adaptive barrier-based controller and a “disturbance-like” term to dampen the oscillation and eliminate the output constraint and backlash nonlinearity for uncertain Timoshenko manipulators.
Unknown disturbances are extensively found in various engineering control systems, the existence of which has great side effects on the control performance of practical engineering systems [31], [32]. Consequently, disturbance rejection has become one of the key control objectives during the design process. Due to the significance of disturbance attenuation, many disturbance rejection control methods have been proposed to handle the undesirable effects caused by unknown disturbances in recent years [31], [33]-[36]. The authors in [31] explored disturbance estimation approaches including linear and nonlinear DOs for industrial control systems. In [33], a nonlinearity estimator-based robust control was devised to stabilize nonlinear systems influenced by nonlinear uncertainties, control gain uncertainty, and external disturbances. In [34], an adaptive neural control with DOs was constructed for the flapping wing aerial vehicle to address the attitude and position control and neutralize the adverse influence of disturbances. In [35], by treating wind effects as unknown disturbances, a nonlinear DO-based control (DOBC)with neural approximations was developed for hypersonic flight vehicles. In [36], a disturbance interval estimation-based antidisturbance control scheme was employed to approximate the time-varying boundaries for disturbances. It is noteworthy that the above-mentioned approaches were only effective for ODE systems and are invalid for PDE systems. Recently,wide concern has been aroused in the DOBC for flexible manipulator systems [37], [38]. In [37], the authors proposed a boundary DOBC for estimating the first-order time differentiation of disturbances. In [38], the modeling and DOBC design were addressed for flexible Timoshenko manipulators possessing extraneous disturbances. However,the DOBC design presented in [37], [38] was confined to eliminating the oscillation and tracking the boundary disturbances and their first-order time differentiations in flexible manipulator systems. To the best of our knowledge,although great progress has been made in DOBC boundary control for flexible manipulators, little research has been reported on the development of finite-time convergence disturbance rejection control for simultaneously suppressing the vibration and handling external disturbances for flexible Timoshenko manipulators, which motivates this research.
In this study, we intend to present a finite-time convergence disturbance rejection control design for stabilizing and controlling a flexible Timoshenko manipulator subject to extraneous disturbances. The main contributions are: 1) Three DOs and boundary controllers are constructed to suppress the shear deformation and elastic oscillation, position the manipulator in a desired angle, and guarantee the finite-time convergence of disturbances; 2) The derived finite-time convergence DOs can make disturbance estimation errors converge to zero in a finite time; and 3) The proposed control schemes ensure the uniformly bounded stability in the controlled system without simplification of infinitedimensional system dynamics.
The rest of this paper is organized as follows. The dynamics of the Timoshenko manipulator system are presented in Section II. The design of finite-time convergence disturbance rejection control scheme is presented in Section III. Numerical examples are simulated and discussed in Section IV. The conclusion is finally drawn in Section V.
II. PROBLEM STATEMENT
A vibrating flexible Timoshenko manipulator system is illustrated in Fig. 1. Let t and q be independent time and space variables, ω(q,t) describes the elastic deflection of the manipulator with length s, inertia per unit length Iρ, mass of unit length ρ, cross-sectional area A, and bending stiffness EI,χ(q,t), θ(t), and θdrepresent the rotation of the manipulator's cross-section, the hub's angle position, and a desired angle position, respectively, the displacement z(q,t) is formulated as z(q,t)=qθ(t)+ω(q,t), γ1(t) denotes the control input torque on the hub with inertia Ih, u(t) and γ2(t) represent the control input and control torque acting on the tip payload with inertia Jand mass M, respectively, and di(t), i=1,2,3 represent external disturbances.

Fig. 1. Flexible Timoshenko manipulator.
Remark 1: For simplification, we define notations as(⋆)=(⋆)(q,t) , (⋆)′=∂(⋆)/∂q, (⋆˙)=∂(⋆)/∂t,(⋆)′′=∂2(⋆)/∂q2, and ( ⋆¨)=∂2(⋆)/∂t2.
The dynamics of the Timoshenko manipulator system under consideration in this study is given as [39]

III. CONTROL DESIGN
A. Preliminaries
We first put forward the following lemmas and assumptions:
Lemma 1 [40]-[42]: Let ν1(q,t),ν2(q,t)∈R with(q,t)∈[0,s]×[0,+∞) . The following inequality is derived for ψ >0:


B. Disturbance Observers Design

C. Boundary Control
Then, the following boundary controllers are designed as


IV. SIMULATIONS


Case 1: d1(t)=d2(t)=(sin(10πt)+cos(3πt))/4 andd3(t)=cos(3πt).
Case 2: d1(t)=d2(t)=(sin(0.1πt)+cos(0.2πt))/4 andd3(t)=0.1cos(0.3t).
When the manipulator system is simulated in Case 1, the responses are presented in Figs. 2-12. In Case 2, the responses of the manipulator system are portrayed in Figs. 13-21. Figs. 2 and 3 display the spatiotemporal response of the vibrating manipulator system in the free case, namely,u(t)=γ1(t)=γ2(t)=0. Under the action of the presented schemes with the setting of design parameters as: k1=45, k2=20, k3=250,k4=1, k5=6 , κ1=κ4=κ7=1, κ2=κ6=κ8=18, κ3=κ6=κ9=10, a1=b1=c1=5, and a2=b2=c2=7, Figs. 4, 5, 13,and 14 depict the 3D representation of the manipulator system in Cases 1 and 2. Figs. 6 and 15 show the time history of the angle position in Cases 1 and 2. The DE errors in Cases 1 and 2 are described in Figs. 7-9 and 16-18. The responses of the presented control u(t) and control torques γ1(t) and γ2(t) in Cases 1 and 2 are respectively portrayed in Figs 10-12 and 19-21.

Fig. 2. Deflection of flexible link without control.

Fig. 3. Rotation of flexible link without control.
To further validate the performance of the derived controllers and DOs, we also provide a simulation with the nonlinear DOBC (40)-(48) formulated as


Fig. 4. Deflection of flexible link with proposed control in Case 1.

Fig. 5. Rotation of flexible link with proposed control in Case 1.
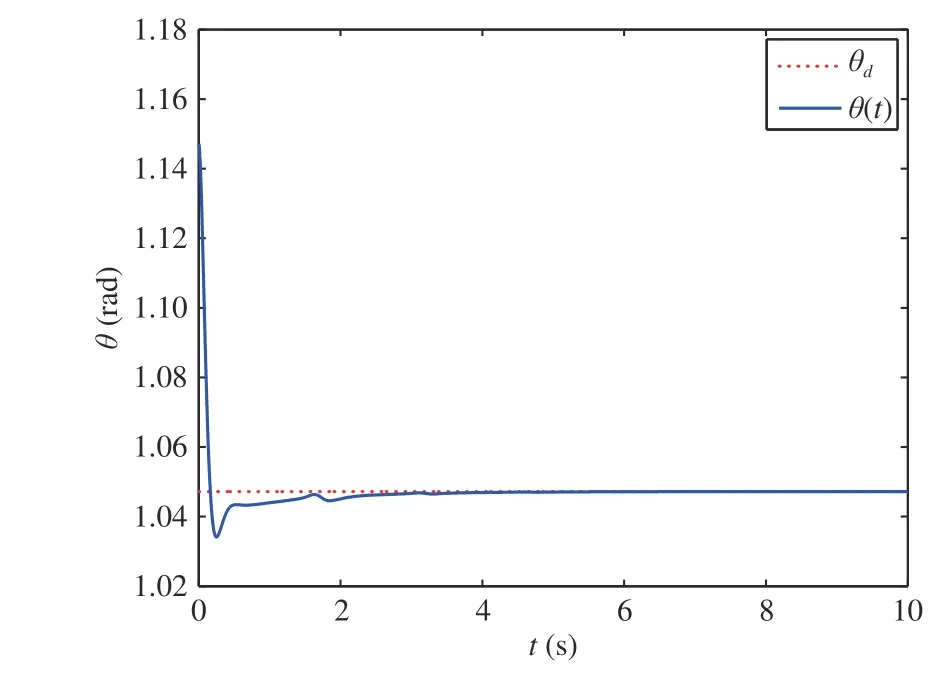
Fig. 6. Angle position of flexible link with proposed control in Case 1.
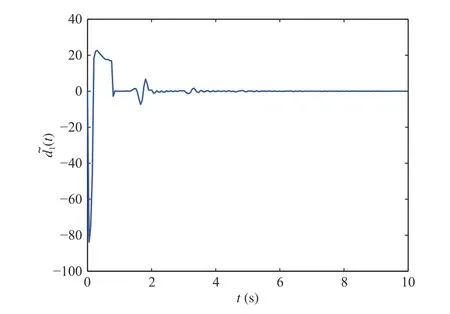
Fig. 7. Disturbance estimation error d ~1(t) in Case 1.

Fig. 8. Disturbance estimation error d ~2(t) in Case 1.
Fig. 9. Disturbance estimation error d ~3(t) in Case 1.
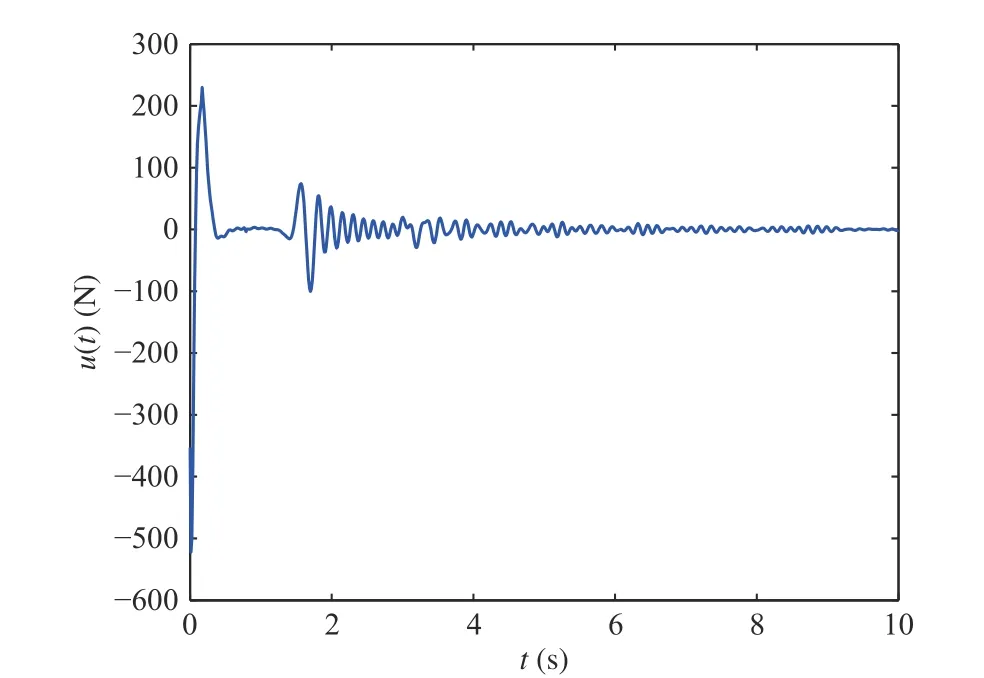
Fig. 10. Control input force u (t) in Case 1.


Fig. 11. Control input torque γ 1(t) in Case 1.

Fig. 12. Control input torque γ 2(t) in Case 1.
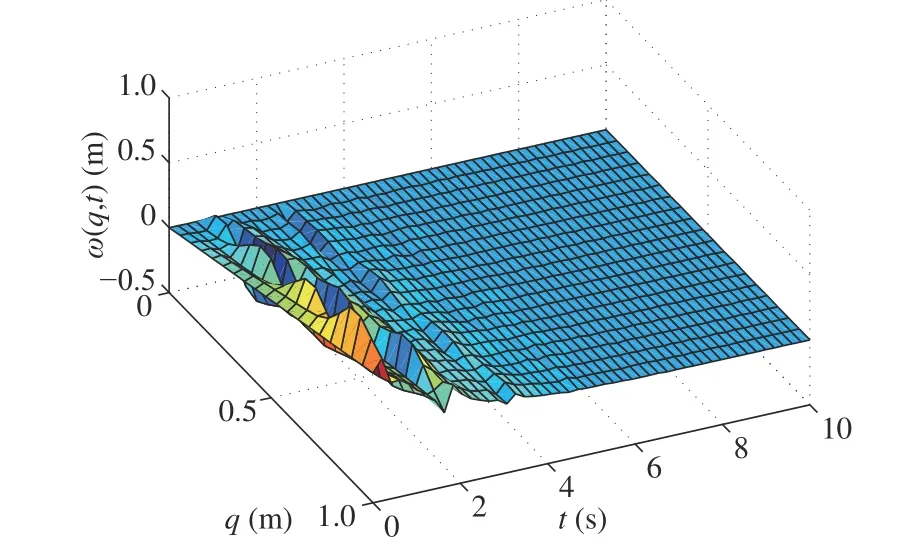
Fig. 13. Deflection of flexible link with proposed control in Case 2.

Fig. 14. Rotation of flexible link with proposed control in Case 2.

Fig. 15. Angle position of flexible link with proposed control in Case 2.

Fig. 16. Disturbance estimation error d ~1(t) in Case 2.

Fig. 17. Disturbance estimation error d ~2(t) in Case 2.


Fig. 18. Disturbance estimation error d ~3(t) in Case 2.
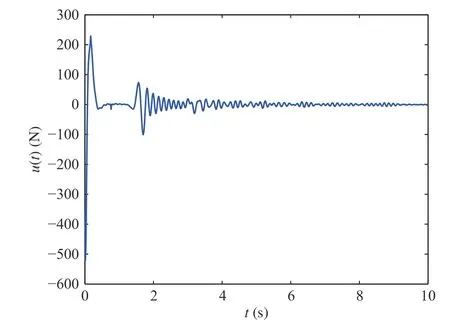
Fig. 19. Control input force u (t) in Case 2.

Fig. 20. Control input torque γ 1(t) in Case 2.
The simulation results Figs. 2-30 show that the devised control can effectively dampen the manipulator's vibration and shear deformation and put the manipulator in the expected angle, achieving a better control performance than the DOBC(40)-(48); and the DE errors under the derived control can converge to zero in a finite time while the DE errors under the DOBC (40)-(48) fluctuate around the equilibrium position. In brief, we draw conclusions that the obtained control can better stabilize the manipulator system as well as ensure the finite time convergence of the DE errors no matter whether high or low frequency disturbances are acted on the system.

Fig. 21. Control input torque γ 2(t) in Case 2.
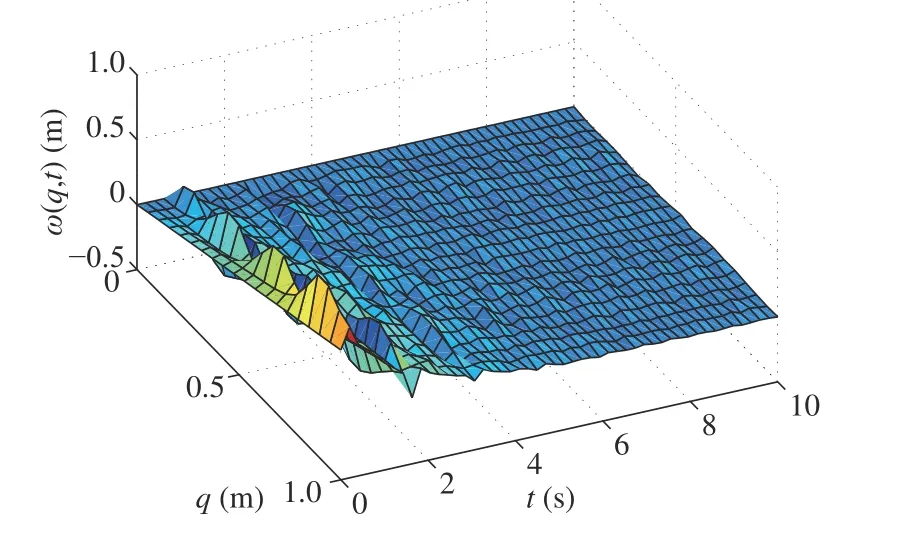
Fig. 22. Deflection of flexible link with DOBC (40)-(48) in Case 1.

Fig. 23. Rotation of flexible link with DOBC (40)-(48) in Case 1.

Fig. 24. Angle position of flexible link with DOBC (40)-(48) in Case 1.

Fig. 25. Disturbance estimation error d ~1(t) with DOBC (40)-(48) in Case 1.Fig. 28. Control input force u (t) with DOBC (40)-(48) in Case 1.

Fig. 26. Disturbance estimation error d ~2(t) with DOBC (40)-(48) in Case 1.Fig. 29. Control input torque γ 1(t) with DOBC (40)-(48) in Case 1.

Fig. 27. Disturbance estimation error d ~3(t) with DOBC (40)-(48) in Case 1.Fig. 30. Control input torque γ 2(t) with DOBC (40)-(48) in Case 1.
V. CONCLUSIONS
We have explored the vibration attenuation, angle orientation, and disturbance rejection issues for flexible Timoshenko manipulator systems subject to external disturbances in this study. Novel finite-time convergence disturbance rejection control schemes were developed for weakening external disturbances, achieving angle tracking,and restraining vibration and shear deformation. With the constructed controllers and DOs, the controlled system was demonstrated to be uniformly bounded and the finite time convergence of DE errors was guaranteed. Ultimately,simulation comparison results manifested the control performance of the suggested schemes. Future research directions include intelligent control approaches [58], [59] for manipulator systems.
APPENDIX A PROOF OF PROPERTY 1
Proof: Differentiating E1(t) and invoking (12) and (13), we have


APPENDIX B PROOF OF LEMMA 4
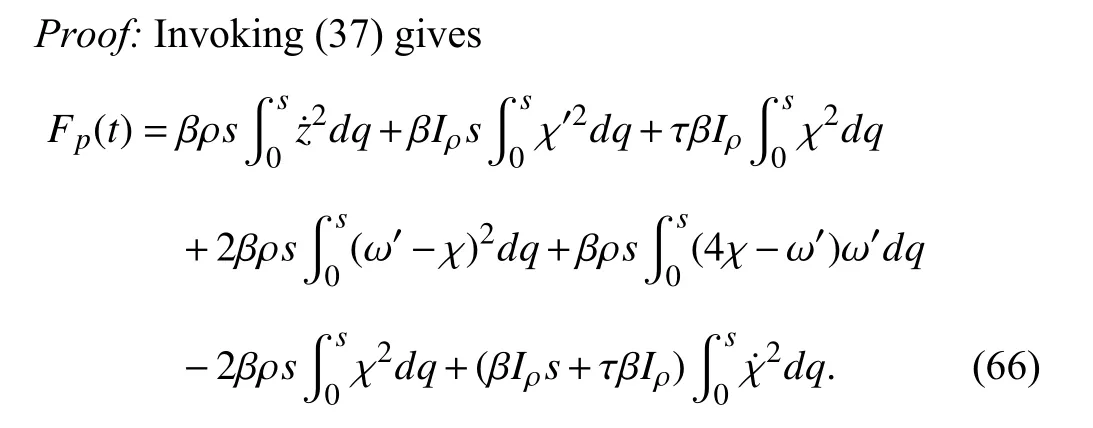
Employing Lemmas 1 and 2 on (66) yields

APPENDIX C PROOF OF LEMMA 5


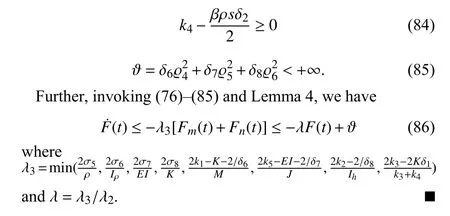
APPENDIX D PROOF OF THEOREM 1

杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- A Multi-Layered Gravitational Search Algorithm for Function Optimization and Real-World Problems
- Dynamic Hand Gesture Recognition Based on Short-Term Sampling Neural Networks
- Dust Distribution Study at the Blast Furnace Top Based on k-Sε-up Model
- A Sensorless State Estimation for A Safety-Oriented Cyber-Physical System in Urban Driving: Deep Learning Approach
- Theoretical and Experimental Investigation of Driver Noncooperative-Game Steering Control Behavior
- An Overview of Calibration Technology of Industrial Robots
