Parametric Transformation of Timed Weighted Marked Graphs: Applications in Optimal Resource Allocation

Zhou He, Member, IEEE, Ziyue Ma, Member, IEEE, Zhiwu Li, Fellow, IEEE, and Alessandro Giua, Fellow, IEEE

Abstract—Timed weighted marked graphs are a subclass of timed Petri nets that have wide applications in the control and performance analysis of flexible manufacturing systems. Due to the existence of multiplicities (i.e., weights) on edges, the performance analysis and resource optimization of such graphs represent a challenging problem. In this paper, we develop an approach to transform a timed weighted marked graph whose initial marking is not given, into an equivalent parametric timed marked graph where the edges have unitary weights. In order to explore an optimal resource allocation policy for a system, an analytical method is developed for the resource optimization of timed weighted marked graphs by studying an equivalent net.Finally, we apply the proposed method to a flexible manufacturing system and compare the results with a previous heuristic approach. Simulation analysis shows that the developed approach is superior to the heuristic approach.

I. INTRODUCTION

MANY artificial systems that consist of a limited quantity of resources shared by different tasks can be classified as resource allocation systems [1]; among them include flexible manufacturing systems, traffic transportation systems,and logistics systems [2]-[7]. Performance of flexible manufacturing systems is usually affected by timing specifications and resource allocation. For the sake of improving productivity and saving cost considerations, the resources of a flexible manufacturing system must be well allocated. The resource optimization of manufacturing systems with operation delay, assembly, disassembly, and batch processing, is a challenging problem for manufacturing engineers.

Timed Petri nets (TPNs) are a model of discrete event systems that are widely applied to control, performance evaluation, and fault diagnosis in timed systems, e.g., flexible manufacturing systems [8]-[11]. As an important subclass of TPNs, timed marked graphs (TMGs) are suitable to model and analyze synchronization appearing in discrete event systems[12], [13].

The performance of a system modeled with TMGs was usually characterized by the cycle time. When the initial marking of a TMG is given, a linear programming is developed to estimate the cycle time [14]. The properties of cyclic TMGs were explored in [15] and it was shown that the evolution of cyclic TMGs is periodic. Therefore, it is possible to estimate the cycle time by analyzing its periodical behaviors. In addition, the linear algebraic approaches can also be applied to model and analyze the dynamic behavior of TMGs [16], [17].

To make a trade-off between the throughput of manufacturing systems and the resource cost, two main resource optimization problems were investigated in the literature: marking optimization [18] and cycle time optimization [19], [20]. The marking optimization problem finds a minimal cost marking such that the system's cycle time does not fall short of a predefined upper bound and the cycle time optimization problem investigated in [20] explores a minimal cycle time marking such that the cost of the machines/resources does not exceed an upper bound.Deadlock control of flexible manufacturing systems is another important problem that has been extensively investigated in a class of Petri nets (PNs) [21]-[23].

For modelling, analyzing, and controlling flexible manufacturing systems with batch processing, a possible method is to use timed weighted marked graphs (TWMGs)[24]. TWMGs have been proven to be adequate for performance evaluation and resource optimization of jobshops, kanban systems, and flexible manufacturing systems that are decision free [14], [15]. In such nets, each place has a unique output transition and a unique input transition but the weights on edges may be greater than one, to represent multiple edges. The behaviors and properties of TWMGs were investigated in [25]. Due to the existence of multiplicities(weights) on edges, the analysis of TWMGs is a challenging problem. When the initial marking of a TWMG is given, its cycle time could be analyzed by converting to an equivalent TMG [26], [27] using the well-known linear programming approach in [14]. However, when the initial marking becomes a decision variable to be determined for an optimization problem, the approaches developed in [26], [27] cannot be directly used. Heuristic methods were developed in [28], [29]for the marking optimization problem of TWMGs to obtain a sub-optimal solution.

By transforming a TWMG whose initial marking is unknown into a finite number of equivalent TMG classes, an optimal initial marking can be obtained by solving a mixed integer linear programming problem for each equivalent TMG class [30], [31]. However, these approaches have high computational cost since the number of equivalent TMG classes increases exponentially w.r.t. the number of places of the original TWMG. In practice it is inefficient to solve a resource optimization problem by exploring all the equivalent TMGs1Although several techniques that may help to speed up the approaches in[30], [31] are developed, these procedures are still subject to high computational complexity..

To this end, this paper proposes a method to convert a TWMG whose initial marking is unknown to an equivalent parametric TMG system that fully describes the finite family of TMGs equivalent to the original TWMG. Using this transformation, a resource optimization problem for the original TWMG can be reduced to an optimization problem for the equivalent parametric TMG, which, as shown later, can be solved more efficiently. Particularly, this approach is used to handle the marking optimization of TWMGs by solving a mixed integer quadratically constrained programming problem for the equivalent parametric TMG system. To the best of our knowledge, the existing results for the marking optimization problem of TWMGs are all based on heuristic strategies.

The main contributions of this work are as follows:

1) We develop an approach to transform a TWMG, whose initial marking is not given, into an equivalent parametric TMG system that fully describes the finite family of TMGs equivalent to the original TWMG.

2) We propose a mixed integer quadratically constrained programming problem for the marking optimization problem of TWMGs.

3) We test the proposed approach on different cases and compare its performance with a previous heuristic approach.

This paper is organized in six sections. The basics of PNs is given in Section II. A method developed in [26] to transform a TWMG whose initial marking is given into an equivalent TMG is introduced in Section III. In Section IV, an approach to transform a TWMG whose initial marking is not given into an equivalent parametric TMG system is presented. In Section V,an analytical approach for the resource optimization problem is developed based on the equivalent parametric TMG system.In Section VI, we give the conclusions.

II. BACKGROUND

A. Petri Nets

A Petri net (PN) is a four-tuple N=(P,T,Pre,Post), where P={p1,...,pn} is a set of n places, T ={t1,...,tm} is a set ofm transitions with P∪T ≠Ø and P∩T =Ø, Pre:P×T →N and Post:P×T →Nare the pre-incidence and post-incidence

Fig. 1. A place pi with an input transition t in(p) and an output transitiontout(p).

B. Cycle Time of TWMGs

There mainly exist three ways of introducing the timing parameters in PN models, i.e., a delay can be associated with transitions, places, or arcs [32]. In this paper, we consider TPNs, in which each transition is associated with a deterministic firing delay. A timed PN is a pair (N,δ), where Nis a PN, and δ :T →N is a firing delay function that assigns to each transition a non-negative integer [30]. The single server semantic is considered in this paper, which means that at each time an enabled transition cannot fire more than once.More details can be found in [32].

For a TWMG system 〈N,M〉, the cycle time is defined as the average period to fire one time the minimal T-semiflow as soon as possible, denoted by χ(M). In [14], a linear programming was developed to obtain a cycle time lower bound as follows:

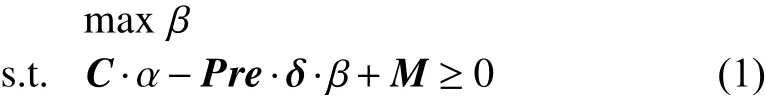
where β ∈R+is the throughput (inverse of the cycle time, i.e.,β=1/χ(M)) and α ∈ Rmare the decision variables. Note that LPP (1) provides an exact value for the cycle time of a TMG system 〈N,M〉. In addition, by simulating the dynamic behavior of a TWMG system [29], the cycle time can also be obtained.

III. TRANSFORMATION OF A TWMG SYSTEM

For a TWMG system, an analytical approach to evaluate the cycle time is to transform it into an equivalent TMG system that has the same cycle time. In [26], Munier proposed a method to convert a TWMG system 〈 N,M〉 (with n places and m transitions) to an equivalent TMG system 〈Nˆ, Mˆ〉 (withnˆ places and mˆ transitions) whose cycle time is identical. This procedure is shown in Algorithm 1.

As discussed in [30], for a TWMG system the structure of its equivalent TMG depends on the initial marking. In addition, the number of equivalent TMG systems of a TWMG, whose initial marking is not given, increases exponentially with the size of place set, which makes the resource optimization problem where the initial marking is unknown quite difficult to solve2The solutions developed in [30] and [31] for the cycle time optimization have high computational cost since they require one to solve a mixed integer linear programming for each possible equivalent TMG system..

Example 1: Consider a TWMG N in Fig. 2 whose minimal T-semiflow is x = (2, 1)T. We assume that the initial marking is M=(2,0)T. According to Algorithm 1, an equivalent TMG system 〈 Nˆ, Mˆ〉 is obtained as follows.

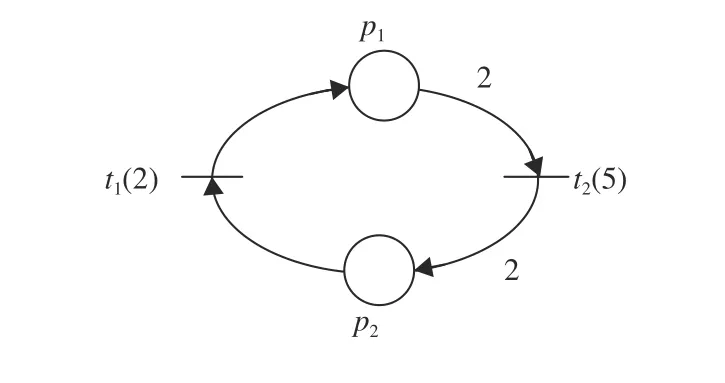
Fig. 2. A TWMG N considered in Examples 1, 2 and 3.

Fig. 3. The equivalent subsystem 〈 Nˆt, Mˆt〉 of transitions.

Algorithm 1 [26] Transformation of a TWMG System into an Equivalent TMG System Under Single Server Semantics Input: A TWMG system with a minimal T-semiflow〈N,M〉x=(x1,...,xm)T〈ˆN, ˆM〉〈N,M〉Output: An equivalent TMG system whose cycle time is identical to〈ˆNt, ˆMt〉ti ∈T xi t1it2i... txi i 1: (Equivalent subsystem of transitions) Replace each transition by transitions, , , , , with delay time ˆδ(tj i)=δ(ti), j=1,...,xi. (2)xi q1i ... qxi i qai a=1,...,xi-1 tai ta+1i qxi i Add places , , , where ( ) is a place connecting to with unitary weights and is a place connecting to with unitary weights.txi i t1i■■■■■■■■■ˆM(qai)=0, i=1,...,m, a=1,...,xi-1 ˆM(qxi i )=1.(3)〈ˆNp, ˆMp〉pi ∈P w(pi)＞v(pi) ni=xin(pi) psi s=1,...,ni 2: (Equivalent subsystem of places: Case 1) Replace each place such that by places , where for:■■■■■■■■■■■■■■■⌋as·xout(pi)+bs=⌊M(pi)+w(pi)·(s-1)+1 bs ∈{1,...,xout(pi)}as ∈N.v(pi)(4)n(pi) tbsout(pi) as Place connects transition to transition and contains ps i tsi tokens, i.e.,■■■■■■■■■■■■■■■in(pi), or equivalently Post(psi,tsin(pi))=1 tout(psi)=tbsout(pi), or equivalently Pre(psi,tbsout(pi))=1 μ(ps tin(psi)=ts(5)i)= ˆM(psi)=as.〈ˆNp, ˆMp〉pi ∈P w(pi)≤v(pi) ni=xout(pi) psi s=1,...,ni 3: (Equivalent subsystem of places: Case 2) Replace each place such that by places , where for:■■■■■■■■■■■■■■■⌉cs·xin(pi)+ds=⌈s·v(pi)-M(pi)w(pi)ds ∈{1,...,xin(pi)}cs ∈Z≤0.(6)psi tdsin(pi) tsout(pi)-cs Place connects transition to transition and contains tokens, i.e.,■■■■■■■■■■■■■■■tin(psi)=tds in(pi)or equivalently Post(psi,tds in(pi))=1 tout(psi)=tsout(pi) or equivalently Pre(psi,tsout(pi))=1 μ(psi)= ˆM(psi)=-cs.(7)〈ˆN, ˆM〉4: (Equivalent TMG system ) The TMG system is equivalent to the union of the subsystems of transitions and places, i.e.,〈ˆN, ˆM〉=〈ˆNt, ˆMt〉∪〈ˆNp, ˆMp〉. (8)

Fig. 4. The equivalent subsystem 〈 Nˆp, Mˆp〉 of places.

Finally, we obtain the equivalent TMG system 〈Nˆ, Mˆ〉 by combining the equivalent subsystems of transitions and places as shown in Fig. 5.

IV. PARAMETRIC TRANSFORMATION OF TWMGS

Since the equivalent structure of the TMG depends on the initial marking of the TWMG, the number of equivalent TMG systems of a TWMG whose initial marking is unknown could increase exponentially with the size of place set. Therefore, it is practically inefficient to solve a resource optimization problem by exploring all the equivalent TMG systems. This section proposes a method to transform a TWMG whose initial marking is not given into an equivalent parametric TMG system. First, we discuss the logic constraints of the possible equivalent subsystems in Section IV-A. Then, some techniques are introduced to convert a TWMG to an equivalent parametric TMG in Section IV-B.

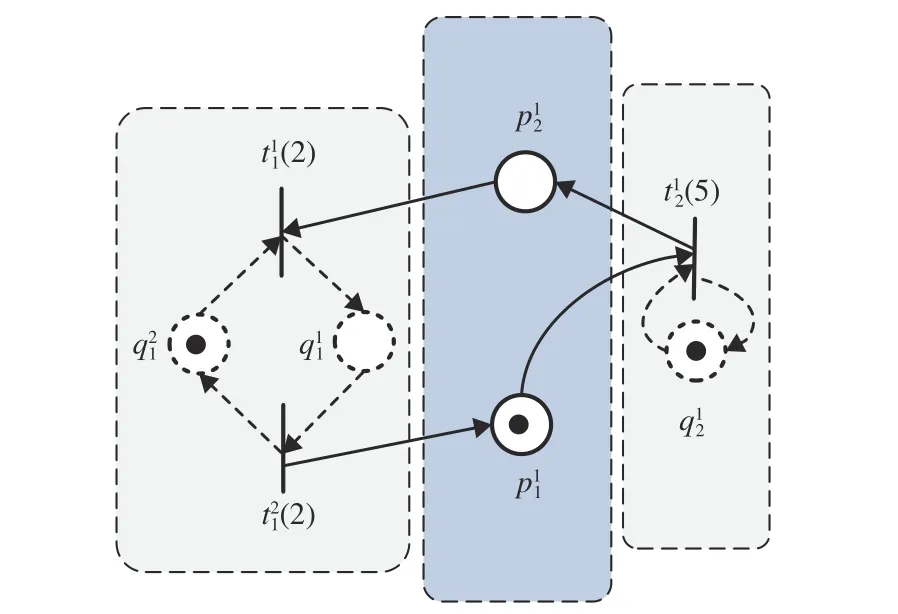
Fig. 5. The equivalent TMG system of the TWMG N depicted in Fig. 2 with M=[2,0]T.

A. Logic Constraints of the Equivalent Subsystems

B. Parametric Transformation

For each place p ∈P, the logic constraints of its possible equivalent subsystems are logic or constraints. In particular,all the constraints are equality constraints. In this subsection,some transformation rules to convert logic or constraints into linear constraints are adopted to synthesize all equivalent subsystems into one.

Consider the following equality constraints:

The work in [33]-[35] showed that the above equality constraints can be transformed into following linear constraints:

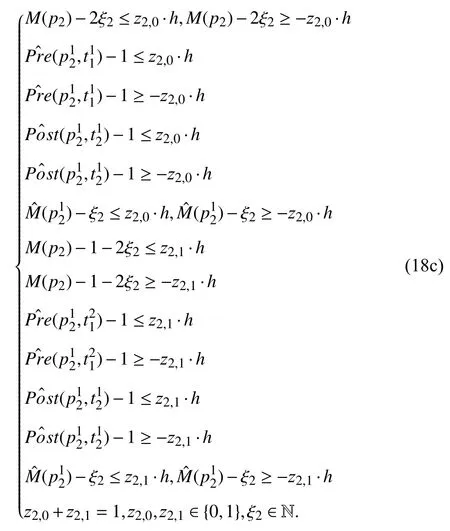
V. APPLICATION TO THE RESOURCE OPTIMIZATION PROBLEM

A. An Optimal Solution for Marking Optimization

This section demonstrates that the transformation approach discussed in Section IV can be further used to handle the marking optimization of TWMGs [28], [29]. Then, an optimal solution based on mixed integer quadratically constrained programming is developed.

The mathematical model of the marking optimization of a TWMG can be summarized as follows [29]:

It is worth mentioning that a mixed integer quadratically constrained programming is a non-convex optimization problem and thus a local optimal solution, which is easy to find, cannot guarantee global optimality [36].

This subsection is concluded with some discussion on its application to the cycle time optimization of TWMGs.Optimal approaches have been developed for TWMGs [30],[31]. However, theses approaches rely on solving mixed integer linear programming for a finite family of equivalent TMGs whose number could increase exponentially w.r.t. that of places. The transformation method proposed in this paper could also be used to the cycle time optimization of TWMGs with a similar technique as Proposition 2.

B. Illustrative Examples

This section applies the proposed approach to the marking optimization of a flexible manufacturing system (FMS) and the obtained results are compared with a previous approach in[29] that is based on the heuristic strategy.

Consider the TWMG of an FMS [28] depicted in Fig. 6. It consists of three machines U1, U2and U3and can manufacture two products, namely R1and R2. The production ratio for R1and R2is 60% and 40%, respectively. The manufacturing processes are as follows:R1:U1, U2, U3(denoted by transitions t1, t2, and t3, respectively) and R2: U2, U1(denoted by transitions t4and t5, respectively).Transitions t6, t7, t8, and t9are used to represent the cyclic manufacturing process.

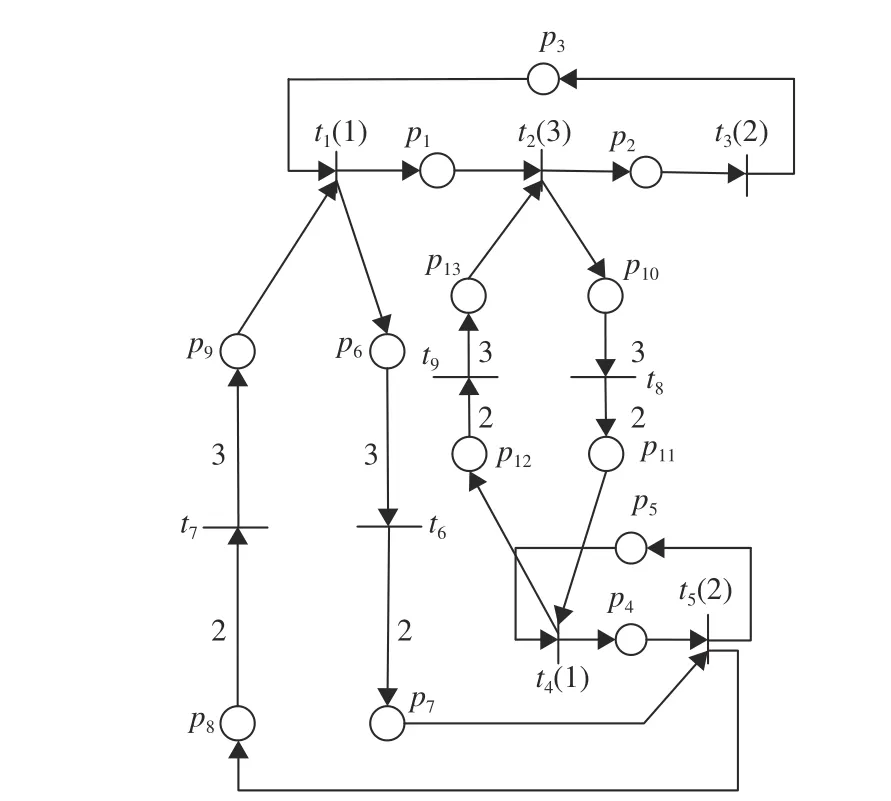
Fig. 6. The TWMG model of a flexible manufacturing system.

In Table I, the proposed approach is compared with the heuristic approach developed in [29] that is implemented by the PN tool HYPENS [38]. All cases run on a computer running Windows 10 with CPU Intel Core i7 at 3.60 GHz and 8 GB RAM. Case 1 is the flexible manufacturing system discussed above, Case 2 is an example taken from Fig. 6 in[29], Case 3 is a flexible manufacturing system studied in[27], and Case 4 is a real assembly line studied in [39] that consists of 41 places and 25 transitions. For each case, the tested approach, the upper bound on the cycle time, the objective function, and the CPU time are shown. Note that the first proposed approach is tested by using LINGO without the global optimal solver option which means that the obtained solution cannot guarantee the optimality, and the second proposed approach is tested by using LINGO with the global optimal solver option. In Table I, “o.o.t” (out of time) means that the solution cannot be found within 12 hours.

The results in Table I show that the locally optimal solutions obtained by the proposed approach (Loc. Opt.) and the heuristic approach in [29] for Cases 1 and 2 are also global optimal. The solution obtained by the heuristic approach in[29] is better than the locally optimal solution for Case 3,while only a locally optimal solution is found for Case 4. It should be noticed that the computational cost for finding an optimal solution is very high with the increase of the net size.Therefore, a locally optimal solution is also useful.

TABLE I SIMULATIONS RESULTS OF THE APPROACH IN [29] AND THE PROPOSED APPROACH

VI. CONCLUSIONS

This work aims to present an approach to transform a TWMG whose initial marking is not given into an equivalent parametric TMG system where the arcs have unitary weights.Using this transformation, a resource optimization problem for the original TWMG can be reduced to an optimization problem for the equivalent parametric TMG, which can be solved more efficiently. Particularly, this approach is used to handle the marking optimization problem of TWMGs and a mixed integer quadratically constrained programming method is developed for the equivalent parametric TMG system. To the best of our knowledge, the existing results for the marking optimization problem of TWMGs are all based on heuristic strategies. Future work aims to extend the developed approach to a general model where shared resources (i.e., conflicts)exist.