卧罐爆炸初始和二次碎片的特征及对立罐前壁和球罐支柱的危害性
2021-04-14李子杰孙东亮
李子杰,孙东亮
(华东理工大学 资源与环境工程学院,上海 200237)
多米诺效应是指危险化学品储罐爆炸产生的破坏性碎片撞击相邻储罐,使相邻储罐发生穿孔或塑性破坏,引发二次事故的现象[1-3]。爆炸碎片是引发多米诺效应的重要因素[4-5],因此,国内外诸多学者对此进行了研究。Gubinelli等[6-7]分析了143起爆炸碎片抛射事故后认为,卧罐事故最多,占70.6%,其次是球罐事故,占7.0%。Hauptmanns等[8]对产生碎片的46起事故进行了分析并认为卧罐爆炸产生的碎片数量服从对数正态分布,平均值为0.855 16,标准差为0.524 48。Mébarki等[9-10]使用最大熵原理研究碎片数量、形状、质量、抛射速度和抛射角度等参数的概率分布。Hu等[11]建立了大型立罐在爆炸冲击波作用下的有限元模型,并对碎片撞击储罐的损伤过程进行了研究。Sun等[12]采用蒙特卡罗模拟方法,研究了储罐爆炸碎片的抛射比例对碎片地面分布、与目标碰撞概率、使目标破裂概率和多米诺效应风险的影响。潘成光等[13]采用有限元分析软件对立方体碎片撞击储罐的过程及变形进行了数值模拟,并发现储罐受撞击产生的变形随碎片初始速度的增大逐渐增大。陈国华等[14]针对尖头碎片撞击小尺寸储罐的过程开展了模拟实验,得到了不同轴向撞击角对穿透形貌、穿透能量以及穿孔直径的影响规律。
先前的研究存在一定的局限性和不足之处。对于碎片的类型,还未研究到安全阀或者液位计这类储罐附件碎片以及爆炸荷载作用下周边建筑产生的脆性二次碎片。在碎片撞击储罐的相关模拟实验中,仅考虑了罐体撕裂所形成的大型碎片,然而在罐体撕裂过程中也会产生小型罐体碎片。对于碎片所造成的化工储罐事故类型考虑并不全面,未考虑碎片撞击球罐支柱等支撑结构的事故后果。
二次碎片是指储罐发生初始爆炸事故之后,其事故后果影响到相邻储罐或周边建筑设施,使它们发生失效破坏而产生的碎片。化工园区的二次碎片一般分为两种:储罐爆炸产生的初始碎片撞击相邻储罐使其发生再次爆炸而产生的二次碎片和储罐爆炸时冲击波产生的超压破坏周围设施产生的二次碎片。Sun等[15]研究了多重多米诺效应并提出了多重多米诺场景的模型:单元1(初始爆炸→碎片)→(破坏)单元2(二次爆炸→碎片)→(破坏)单元3(第三次爆炸→碎片)→(破坏)单元4(第四次爆炸→碎片)→……→(破坏)单元n-1(第n-1次爆炸→碎片)→(破坏)单元n。从多重多米诺场景的模型可以看出,初始爆炸之后碎片导致的第n-1次爆炸还会产生碎片并导致第n次爆炸,因此对于第n次爆炸,每个n-1次爆炸其实都可以看作独立的初始爆炸,其爆炸产生的碎片性质等同于初始爆炸所产生的碎片性质。
因此,综合考虑卧罐爆炸本体与安全附件碎片以及周边设施破坏后产生的二次碎片,按照文献[16]的爆炸事故类型,统计并分析文献[6-9,17-19]中的碎片数量,探索并建立卧罐爆炸初始与二次碎片的数量、质量与速度的概率分布模型。利用LS-DYNA软件对3种爆炸碎片在不同速度下撞击立罐前壁的过程进行数值模拟研究,获得不同种类爆炸碎片撞击容器后所产生的孔洞直径,分析其失效规律。最后模拟分析爆炸碎片撞击不同尺寸球罐支柱的过程,探究球罐整体失稳的可能性。
1 卧罐爆炸初始和二次碎片的特征
1.1 初始及二次碎片的数量
1.1.1 卧罐本体与安全附件的初始碎片数量
卧罐爆炸事故的类型包括沸腾液体扩散蒸气爆炸(BLEVE)、物理爆炸(ME)、受限空间爆炸(CE)、反应失控(RR)[16]。文献[8-9,17-19]研究了BLEVE事故所产生的碎片数量以及产生不同碎片数量所对应的事故频次,按事故的碎片数量将文献中的事故进行分类统计,所有数据整合结果如表1所示。

表1 卧罐BLEVE事故数据
然而,导致储罐爆炸产生碎片的事故类型不止一种,Gubinelli与Cozzani[6-7]考虑了BLEVE、ME、CE与RR 4种事故后果,并依据历史事故数据库的分析,根据卧罐各爆炸事故情形中的每种破裂形式确定其产生的碎片数量,结果如表2所示。

表2 Gubinelli与Cozzani的卧罐事故数据[6-7]
目前,学者们一致认为卧罐爆炸产生的碎片数量范围为[1,9],且都是储罐本体撕裂产生的大型碎片数量,并没有考虑由于焊接缺陷等原因导致爆炸时弹出的附件数量。JBT 4731—2005《钢制卧式容器》标准中所涉及的卧罐附件包括人孔、安全阀、压力表、液位计、支架和接头焊缝[20]。因此,综合卧罐爆炸后本体和附件碎片的数量,卧罐爆炸产生的碎片数量范围应为[1,15]。需要说明的是,当产生大型碎片之后,储罐内部的压力会得到瞬时释放,高压释放致使焊接断裂并导致附件弹出的可能性很小,即大型碎片与罐体附件碎片同时出现的可能性较小,因此,4种事故类型下产生碎片数量为[10,15]的事故频次总和小于产生9个碎片的事故频次。因此,得到包括罐体本体与安全附件的碎片数量和对应的爆炸事故频次以及同类型爆炸事故中的占比(表3和4)。
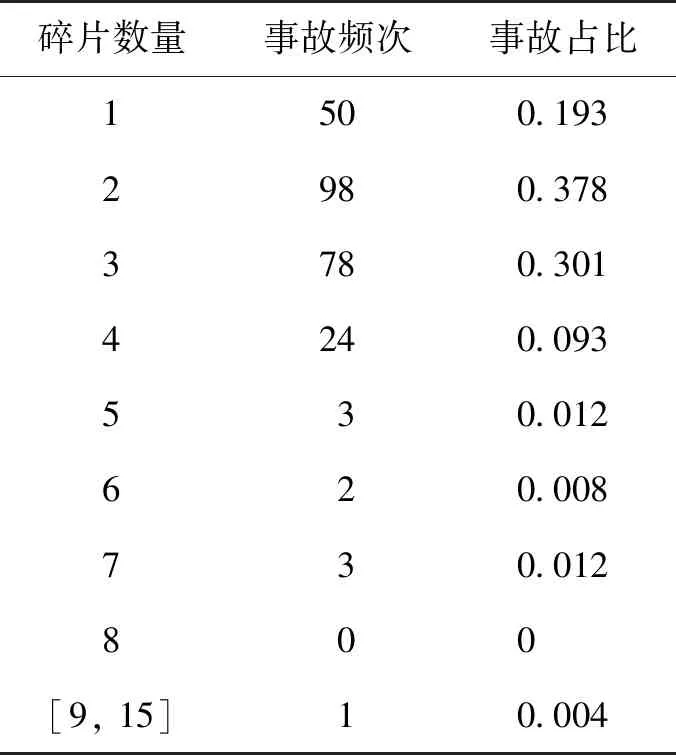
表3 卧罐BLEVE事故所产生的碎片数量和对应的事故频次以及事故占比
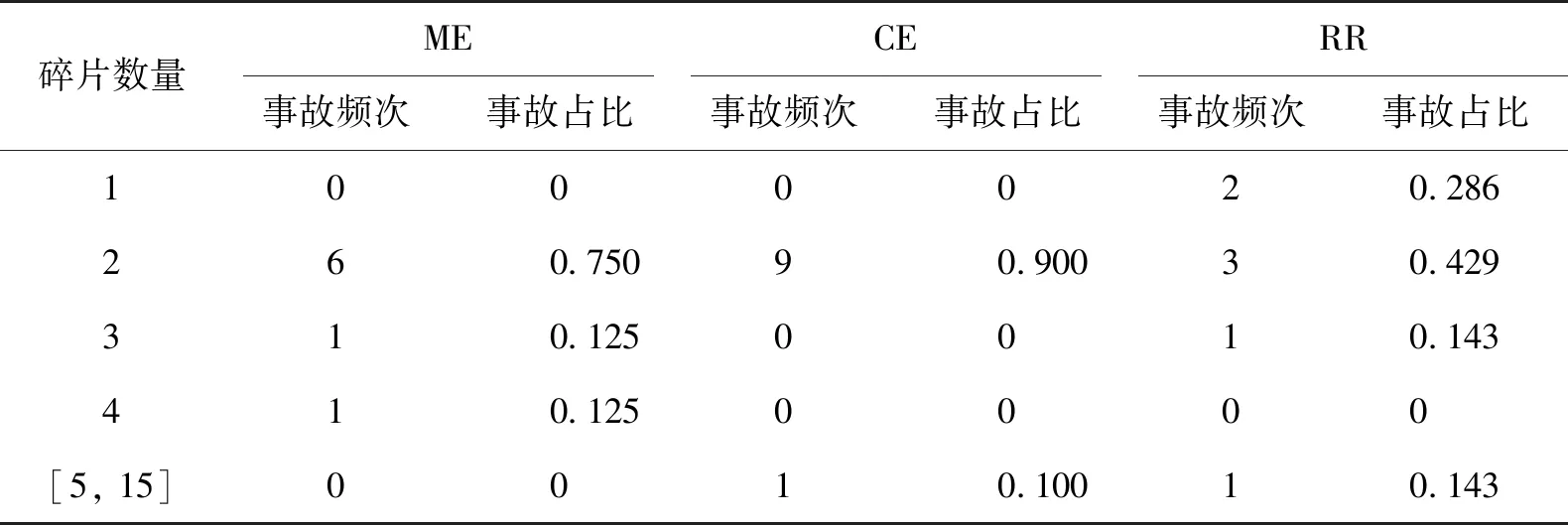
表4 卧罐ME、CE和RR事故所产生的碎片数量和对应的事故频次以及事故占比
由表3和4中数据计算各碎片数量的平均值(E1)和方差(E2),分别见式(1)和(2)。
(1)
(2)
式中po(i)为产生碎片数量i的事故占比。
依据最大熵原理,建立碎片数量概率(P(N))分布模型,见式(3)。
P(N)=e-λ0-λ1N-λ2N2
(3)
式中:N为初始碎片的数量;λ0、λ1、λ2为3个未知的拉格朗日因子。
因此,根据表3和4中的爆炸事故数据,建立式(4)的方程组,计算拉格朗日因子并代入式(3)。最后得到4种爆炸事故类型产生的碎片数量概率分布模型,结果如表5所示。
(4)

表5 碎片数量概率分布模型
1.1.2 周边设施产生二次碎片的数量
化工储罐周围可能存在由脆性材料建造而成的建筑设施。脆性材料在爆炸载荷作用下容易开裂、断裂并形成碎片。这些碎片可能再次影响附近的设施。
汪明[21]利用AUTODYN模拟了砌体填充墙在爆炸冲击作用下的破碎过程,得到了在爆炸荷载作用下形成碎片的广义体积极限分布密度函数。将公式进一步推导,得到周边设施二次碎片的数量概率(P(N′))分布模型,如式(5)所示。
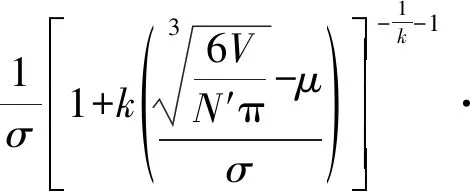
(5)
式中:N′为概率分布函数的独立变量,即二次碎片数量;μ、σ和k为概率参数,分别取0.008 97,0.004 12和0.568 20;V为脆性材料总体积。
1.2 初始和二次碎片的质量
1.2.1 初始碎片的质量
Hauptmanns[8]的研究表明碎片质量由储罐的总质量乘以服从β分布的系数所得。对于卧罐,在不考虑附件时,碎片质量由罐体质量表示,则初始碎片质量(mp)可由储罐和附件总质量推导出,见式(6)。
mp=k′(mt-me)
(6)
式中:mt为储罐总质量;me为附件总质量;k′为服从β分布的系数,k′的β分布概率PK(k′)见式(7),其中,a=0.412,b=1.393。
(7)
1.2.2 周边设施产生二次碎片的质量
以汪明[21]的研究为基础,进一步推导得出二次碎片的质量(ms)概率(P(ms))分布模型,见式(8)。
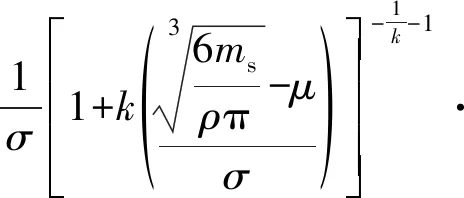
(8)
式中ρ为周边设施材料密度。
1.3 初始与二次碎片的抛射速度
1.3.1 初始碎片抛射速度
根据动能定理,速度可以用式(9)表示。
(9)
式中:vp为初始碎片速度,Ec为每个碎片获得的动能。
每个碎片的动能(Ec)可由总能量(E)导出[9-10],见式(10)—(12)。
Ec=αE
(10)
(11)
Pα(α)=e4.886 9-24.943 1α+0.479 3ln α
(12)
式中:Vt为容器体积,p0为失效压力,pe为大气压力,γ为绝热指数,Pα(α)为倍数因子α的概率分布函数。
1.3.2 周边设施产生二次碎片的抛射速度
储罐爆炸后的破坏效应包括冲击波超压、火灾热辐射和容器破裂产生的碎片。因此,储罐爆炸产生的总能量分别用于冲击波超压、火灾热辐射和爆炸碎片的产生。
冲击波产生的超压破坏周围设施产生二次碎片。根据文献[22]的研究结果,爆炸产生的火焰热辐射约占总能量的10%。因此,冲击波的能量消耗可以用式(13)计算。
Es=0.9E-NEc
(13)
式中Es为冲击波产生超压的总能量。
根据高斯定理,假设作用于二次碎片的能量(Ea)与至爆炸中心距离(r)的平方成反比,见式(14)。
(14)
以动能定理为基础,二次碎片的抛射速度(vs)可表示为式(15)。
(15)
二次碎片数量(N′)服从式(5)的数量概率分布。
2 卧罐爆炸初始和二次碎片对立罐前壁和球罐支柱的危害性
2.1 初始和二次碎片几何模型
卧罐附件包括人孔、安全阀、压力表、液位计等类型,此类附件带有圆形表盘或者其他的圆形结构,表面光滑且棱角较少,笔者将该类附件碎片简化为球体结构。根据Gubinelli等[7]对卧罐爆炸碎片的研究可知,带有厚度的罐壁在受到爆炸冲击时,储罐本体被撕裂成数量≤9的碎片,该类碎片具有长度、宽度以及厚度,笔者将小型罐体碎片简化为立方体结构。根据汪明[21]对爆炸荷载作用下砌体墙破碎过程的模拟研究可知,脆性设施在爆炸荷载作用下,内部形成大量微裂缝,并在较短时间内相交贯通,形成数量较多且尺寸较小的碎片。该类碎片带有鲜明的棱角或尖端,笔者将该类二次碎片简化为圆锥体结构。
综上所述,将爆炸碎片分别简化为等体积的代表附件碎片的球体(半径0.14 m)、代表小型罐体碎片的立方体(边长0.23 m)以及代表二次碎片的圆锥体(底面半径0.19 m,高0.30 m)模型,如图1所示。

图1 碎片几何模型Fig.1 Geometric models of fragments
球体模型(附件碎片)选择HPb63-3型铅黄铜材料,立方体模型(小型罐体碎片)选择与罐体材料一致的Q235a型钢材料,圆锥体模型(二次碎片)选择砖与砂浆的混合体材料,3类材料的特性如表6所示。

表6 材料属性
2.2 撞击立罐后果模拟
2.2.1 模拟参数设定
根据HG 21502.1—1992《钢制立式圆筒形固定顶储罐系列》标准[23],选取相应立式固定顶储罐参数:罐壁高度6 m,内径6 m,壁厚6 mm。由于碎片撞击立罐时仅对储罐的一侧产生影响,因此采用半结构实体建模,如图2所示。

图2 储罐几何模型Fig.2 Geometric models of tanks
利用Ls-Prepost软件对划分好网格的实体进行关键字的定义,使用关键字MAT_PLASTIC_KINEMATIC定义目标容器的材料属性,应变率用Cowper-Symonds模型[24]进行定义,立罐前壁屈服应力(σY)见式(16)。
(16)
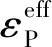
根据顾思阳等[25]对大型立罐的应力分析可知,在表面荷载、重力荷载作用下,罐壁的径向位移较明显,位移较大区域都在罐壁的中上部和罐壁的上沿处,此时不会发生罐体整体偏移。因此,在模拟过程中对储罐两边设置全约束,避免碎片撞击过程中罐体自身的移动,如图3所示。

图3 约束设置Fig.3 Constraint settings
选择CONTACT_ERODING_SURFACE_TO_SURFACE侵蚀接触,该接触类型能够自动删除因网格畸变而变形过大的网格,保证接触依旧在剩余的单元中进行。选择VELOCITY GENERATION关键字定义加载,碎片以30°的角度进行撞击。通过式(9)与(15)的碎片速度可以发现:当爆炸碎片数量一定时,附件碎片、小型罐体碎片以及二次碎片由于质量与体积相对较小,获得的抛射速度较大,结合Mebarki等[26]对碎片速度的计算方法,选取90~150 mm/ms的高抛射速度进行撞击。
2.2.2 模型验证
管公顺等[27]利用球形2017-T4铝弹丸与不同厚度的2A12铝合金板通过二级轻气炮进行超高速撞击实验,得到了不同弹丸撞击速度、弹丸尺寸与穿孔尺寸之间的影响规律。采用本文有限元模型对文献[27]的4组工况实验进行模拟分析,并比较穿孔直径的实验和模拟结果,见表7。

表7 数值模拟与实验结果对照表
由表7可见:模拟结果与文献[27]实验结果的误差范围为1.84%~15.33%,平均误差为8.89%。文献[27]中利用撞击穿孔的经验公式进行孔径大小的预测计算,其预测穿孔直径与实验结果误差为6%,与本模拟结果的平均误差接近。由于本文中所使用的材料参数与文献[27]实验中使用的铝合金参数存在些许偏差,进而造成误差略大。因此,表7的穿孔直径模拟结果是合理的,可以使用本文的有限元模型进行计算模拟。
2.2.3 撞击立罐结果分析
通过LS-DYNA有限元模拟软件模拟附件碎片撞击立罐前壁的过程,得到撞击不同阶段示意图,见图4。

图4 撞击不同阶段示意图Fig.4 Schematic diagram of different impacting stages
通过模拟发现,撞击速度为150 mm/ms时,球体附件碎片在短时间内完成与罐壁的接触、贯穿以及贯穿后飞行的3个阶段,罐壁受到冲击载荷后在接触面区域内形成大量微裂纹,并在极短时间内扩散、交汇,最终形成孔洞。碎片贯穿罐壁后孔洞有轻微的扩张现象,最终的孔洞直径约为380.30 mm。球体附件碎片贯穿罐壁所需时间为0.69 ms,此后碎片的抛射速度降至146.79 mm/ms,如图5所示。
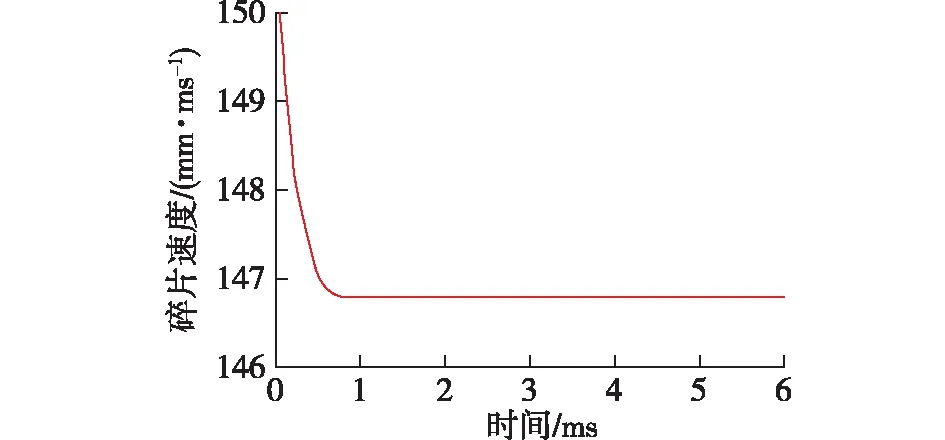
图5 附件碎片速度-时间曲线Fig.5 Velocity-time curve of accessory fragment
罐体表面的应力分布范围随球体附件碎片的侵蚀而逐渐增大。在碎片贯穿罐壁后,孔洞存在4个裂纹尖端,尖端附近应力较强,5 ms后该部分应力依然没有衰减,如图6所示。由图6可得:应力分布于撞击中心周围,且由里向外逐渐减小,高应力的分布范围在碎片完全贯穿罐壁后达到孔洞直径的近3倍。

图6 附件碎片贯穿罐壁5 ms时罐壁等效应力分布Fig.6 Effective stress distribution of the tank wall with accessory fragment penetrated for 5 ms
进一步模拟圆锥体二次碎片撞击罐壁的过程,其贯穿后的罐壁表面应力分布如图7所示。由图7可得:当碎片贯穿罐壁后,孔洞朝水平方向两边扩张,相比球体附件碎片,圆锥体二次碎片在罐壁上生成的整体应力范围较小。

图7 二次碎片贯穿罐壁5 ms时罐壁等效应力分布Fig.7 Effective stress distribution of the tank wall with secondary fragment penetrated for 5 ms
立方体小型罐体碎片撞击罐壁的过程中,其应力分布主要沿孔洞的棱角处扩散。碎片贯穿罐壁后,其孔洞附近的应力迅速衰减,如图8所示。

图8 小型罐体碎片贯穿罐壁5 ms时罐壁等效应力分布Fig.8 Effective stress distribution of the tank wall with small tank fragment penetrated for 5 ms
获取3种碎片撞击时罐体的内能-时间曲线图,如图9—11所示,其中,A代表罐体的整体内能变化趋势,B代表撞击过程中被删去的相关单元的内能变化趋势。由图9—11可以看出:碎片撞击后罐体的整体内能明显上升,球体附件碎片撞击储罐所生成的整体内能最高,在碎片贯穿后达到2.25×104J,其去除破损部分后剩下罐体的内能也最高,达到1.5×104J。

图9 附件碎片撞击时储罐内能-时间分布Fig.9 Internal energy-time curves of tank impacted by accessory fragment

图10 二次碎片撞击时储罐内能-时间分布Fig.10 Internal energy-time curves of tank impacted by secondary fragment

图11 小型罐体碎片撞击时储罐内能-时间分布Fig.11 Internal energy-time curves of tank impacted by small tank fragment
在控制其他参数不变的条件下,对于每种碎片类型,进一步选取90、110、130和150 mm/ms的撞击速度[26]模拟碎片撞击过程,并获取罐壁孔洞数据,将3类碎片的撞击速度与孔洞大小进行对比,结果如图12所示。由图12可见:在较低的撞击速度下,孔洞大小有明显的差异,在高速撞击时,穿孔直径差异很小。3类碎片中,圆锥体二次碎片撞击速度对孔洞直径影响最大,且在低速撞击时无法贯穿罐壁;球体附件碎片撞击速度对孔洞直径影响较小,其速度增长60%时孔洞直径的增长幅度维持在5%以内;立方体小型罐体碎片撞击速度与穿孔直径呈负相关关系。

图12 碎片撞击速度与穿孔直径关系Fig.12 Relationship between velocity and hole size
综合考虑碎片撞击罐壁后形成的孔洞大小、罐体的应力分布以及内能大小,可以得出:当碎片体积相等,以较低速度进行相同角度的撞击时,立方体小型罐体碎片撞击罐壁所形成的孔洞最大。而当撞击速度较高时,球体附件碎片所形成的孔洞最大,其贯穿后罐壁的内能最高,应力分布最广。
2.3 撞击球罐支柱后果模拟
根据GB 12337—2014《钢制球形储罐》标准[28],选择07MnNiMoVDR压力容器用调质高强钢作为球罐以及支柱材料,支柱与球壳的连接方式为赤道相切直接连接型结构。球罐外直径18 m,球罐体积3 000 m3,壳体厚度54 mm,支柱10根,支柱外直径630 mm,支柱壁厚14 mm,支柱高度10 600 mm,拉杆和支柱之间的夹角36°,拉杆直径34 mm,三维模型如图13所示。

图13 球罐模型Fig.13 Model of spherical tank
根据第2.2节中的模拟结果可知,当撞击速度较高时,形成最大孔洞的为球体附件碎片。因此,选择该类型碎片,并设定撞击速度为150 mm/ms,以30°入射角撞击球罐支柱,同时对整个球罐施加重力场。不同时间段受撞击后支柱表面等效应力分布如图14所示。

图14 不同时间段受撞击后支柱表面等效应力分布Fig.14 Equivalent stress distributions on the surface of the impacted pillar during different time periods
根据模拟计算结果可知,碎片贯穿支柱前壁所需时间约为2 ms,完全贯穿支柱需6 ms。碎片撞击球罐支柱过程中,应力均分布于受冲击支柱上,并未涉及球罐本体。7 ms后球罐的整体应力分布如图15所示。
由于大型球罐所含支柱数量比小型球罐多且支柱体积也相对较大,因此,等体积碎片撞击大型球罐支柱与小型球罐支柱时所产生的后果不同。进一步研究碎片撞击15 000和1 000 m3球罐支柱的后果,得到碎片撞击7 ms后两种球罐的应力分布,如图16和17所示。
根据模拟计算结果可知,碎片撞击15 000 m3球罐支柱时,未能穿透支柱前壁,且低应力会逐渐从支柱扩散至球罐,但并未影响球罐整体稳定性。
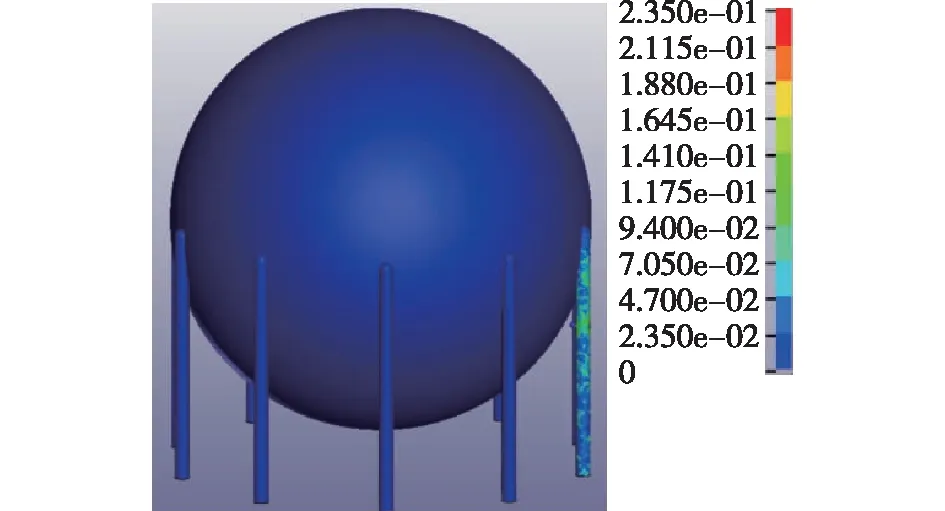
图15 3 000 m3球罐整体应力分布Fig.15 Global stress distribution of spherical tank of 3 000 m3

图16 15 000 m3球罐整体应力分布Fig.16 Global stress distribution of spherical tank of 15 000 m3

图17 1 000 m3球罐整体应力分布Fig.17 Global stress distribution of spherical tank of 1 000 m3
碎片贯穿1 000 m3球罐支柱前壁所需时间约为2.23 ms,完全贯穿支柱需6.3 ms,且球罐表面并未受到应力作用。
3 结论
本文综合考虑卧罐爆炸本体与安全附件碎片以及周边设施破坏后产生的二次碎片,对其特征和对立罐前壁以及球罐支柱的危害性进行研究,所获结论如下:
1)依据最大熵原理以及相关事故数据和文献研究结果,探索并建立了初始及二次碎片数量、质量以及速度概率分布模型,且卧罐爆炸初始碎片数量在统计区间[1,15]内均服从离散指数分布。
2)在碎片体积相等并且碎片抛射角度和抛射速度一致的情况下,圆锥体二次碎片由于其较低的质量,在撞击罐壁过程中速度衰减最明显,贯穿所需能量最大。
3)3种碎片中,圆锥体二次碎片撞击速度对孔洞直径影响最大,且在低速撞击时无法贯穿罐壁;球体附件碎片撞击速度对孔洞直径影响较小,其速度增长60%时孔洞直径的增长幅度维持在5%以内;立方体小型罐体碎片撞击速度与孔洞直径呈负相关关系。
4)当碎片体积相等,以较低速度进行相同角度的撞击时,立方体小型罐体碎片破坏性最大。而当撞击速度较高时,球体附件碎片贯穿罐壁后罐壁的内能最高,应力分布最广。
5)不同尺寸球罐支柱在爆炸碎片撞击作用下均不会发生失稳坍塌现象。
