基于模糊算法的四轮线控转向汽车操稳性研究*

屈文涛，李文锐，高 睿，杨 斌，徐剑波

（1. 西安石油大学机械工程学院，陕西 西安710065；2. 西南油气田纪检审计中心，四川 成都610000；3. 长庆油田分公司第三采气厂，内蒙古 乌审旗017300）

引 言

新能源汽车的研究随着世界能源紧张和环境问题而日益突出[1]。目前四轮转向电动汽车因污染小、转向灵活、易于计算机算法直接控制的特点而被广泛研究。电动汽车转向采用线控技术，取消了传统汽车的机械传动机构，采用四台轮毂电机和四台转向伺服电机分别实现车轮的驱动和转向，车轮的转角可以精确地跟踪和控制。在实际使用时，尤其在无人驾驶的线控转向上应尽量避免车辆在中高速转弯行驶时出现的侧滑和甩尾现象。为了提高线控转向对车辆转弯稳定性的控制，国内外的研究主要表现在线控转向下的前后轮转角分配和控制策略上。经典的转向方法为设置汽车前轮为主动轮，后轮为从动轮并与车身的惯性一起做摆动[2]，常常出现转向不足或转向过度的现象，影响操作稳定性。Sano提出固定转向比的四轮转向系统[3]，但这使得后轮转角的随动性变差，后轮转向的空间被限定。文献[4]阐述了转角比例控制方法，后轮与前轮转角遵循一定的比例，其中比例系数是关于车速及车辆结构参数的量，该比例可使转向时质心侧偏角接近零，操稳性（操纵稳定性）提高，但存在高速时横摆角速度太小致使转向不足的问题。文献[5]提出利用后轮反馈补偿的方法实现横摆率的稳定控制，但又限制了前轮的转向控制余地。因此，本文引入模糊推理下的前轮和后轮转角补偿的联合控制方法来对转弯操稳性进行控制。

1 车辆运动模型建立

车辆运动时需要知道自身在空间坐标系下的位置坐标。而坐标的寻找离不开基准定位点的选取。本文分析的是前后轮转向的四轮转向汽车，其底盘由可以前后自由转向的车轮组成，图1为其运动简图。该运动模型假设：

1）车辆只做平行于地面的平面运动。

2）只考虑前后转向轮对运动轨迹的影响，将系统简化为二自由度自行车模型[6]。

3）为了保证稳态转弯状态下质心侧偏角为零，取前后转向为前馈型后轮转向策略[7]。

图1 车辆自行车运动模型

这里，O为车辆的质心点，XO为质心的位置在绝对坐标系X 轴的分量，YO为质心的位置在绝对坐标系Y 轴上的投影。VO为车辆质心速度，前后轮转角分别为δf和δr，车身角速度为ω，车辆坐标系x轴与绝对坐标系X 轴的偏角为φ。u,v分别为质心速度的纵向分量和横向分量；β 为质心侧偏角。这里规定转角和角速度均逆时针为正和顺时针为负。式（1）与式（2）为质心的点运动方程。式（3）为小车的车辆坐标系x轴与绝对坐标系X 轴的偏角公式。

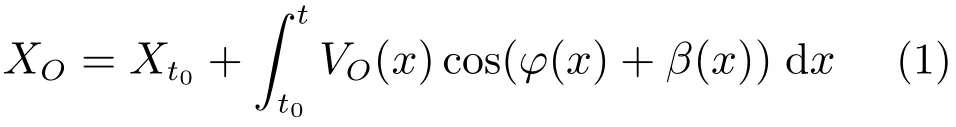
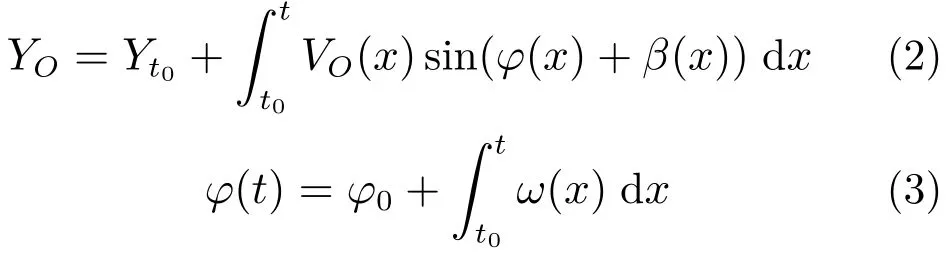
式中：t0为初始运动时刻；t为当前时刻；Xt0和Yt0为质心的初始起点坐标；φ0为初始偏角。

2 二自由度动力学模型建立

为了分析四轮线控转向技术的汽车的路径转弯，在不失准确性的基础上将其简化为二自由度动力学模型[8]，以减少控制算法的计算量，如图2所示。图中：αf为前轮侧偏角；αr为后轮侧偏角；Ff为前轮地面侧向力；Fr为后轮地面侧向力。

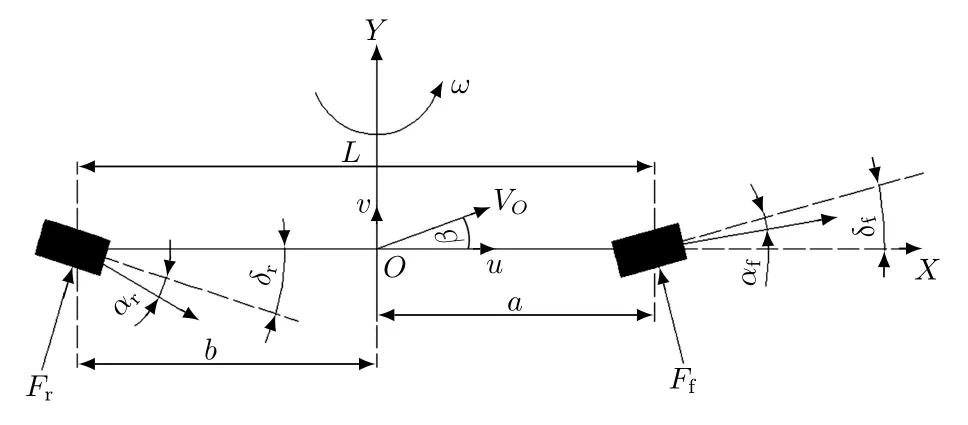
图2 车辆转弯二自由度模型

在研究转向时可以进行以下必要的假设：

1）质心速度的纵向分量u保持不变，四轮转向车辆侧向加速度在0.4g范围内。

2）中高速转弯时的车辆不做加速行驶，忽略回正力矩对转弯的影响，忽略横向和纵向空气动力学。

车体结构、轮胎特性参数设置见表1。

表1 车辆参数

由上述参数可以推得二自由度车辆横摆动力学模型具体公式。设前轮转角为δf，后轮转角为δr，横摆角速度为ω，得到二自由度微分方程：

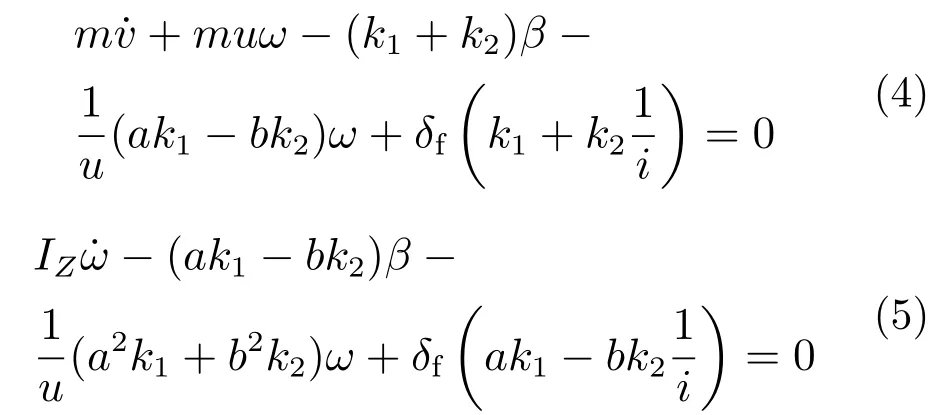
这里后轮输入通过转向比i折算到前轮输入，参考线性二自由度的汽车模型得到如下以前轮转角为输入，以车辆角速度和质心侧偏角为输出的传递函数方程。式（6）为角速度方程，式（7）为质心侧偏角方程，式（8）—式（16）为各参数计算公式。

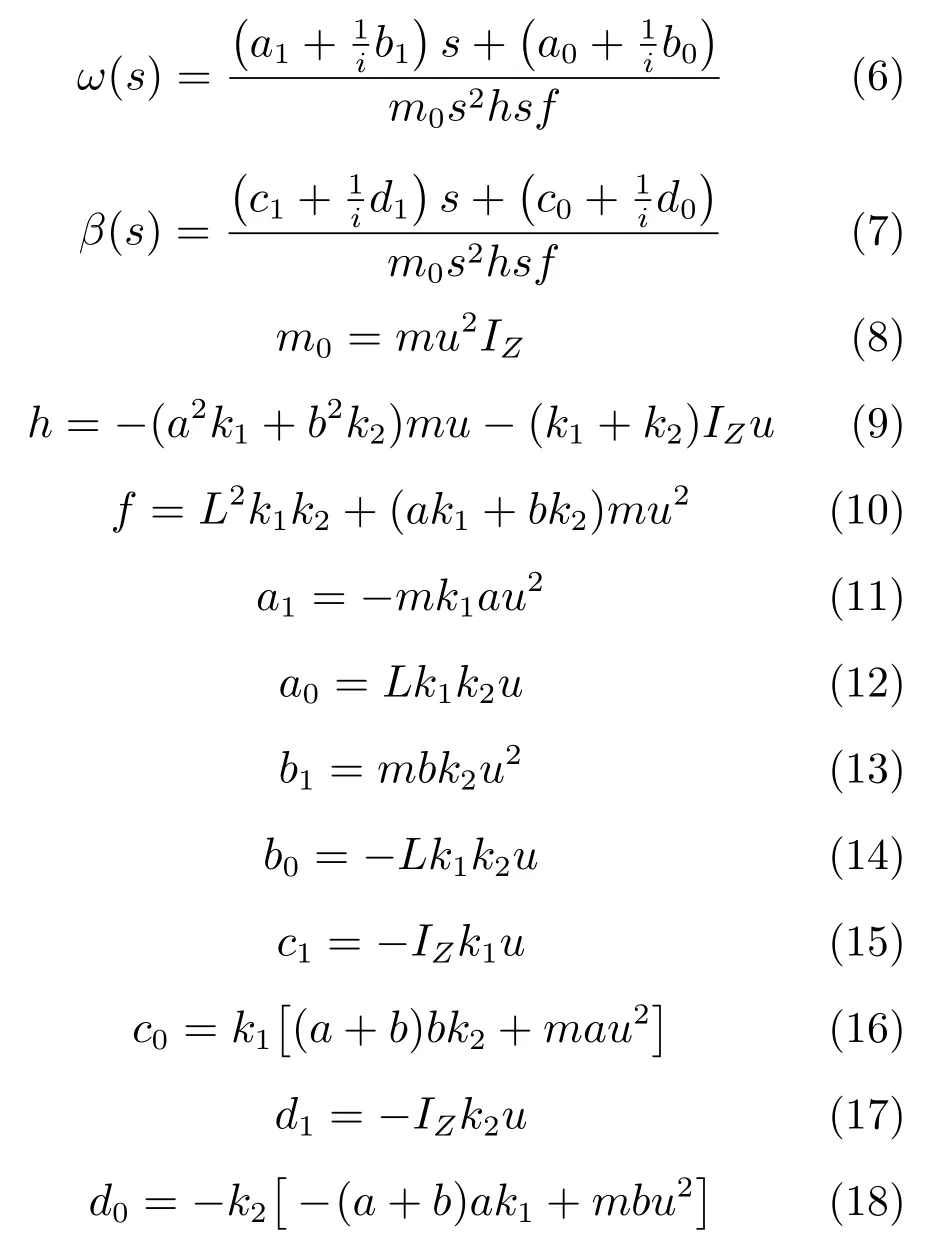
式中，s为拉普拉斯算子。

3 模糊转向补偿控制器设计

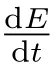
利用前轮给定转角先估算出稳态横摆角速度值，将此值与实际动态的横摆角速度比较后反馈给模糊PID，利用前轮比例前馈值和模糊PID来决定后轮应补偿的角度大小[9]。但是，这种策略限制了前轮转向的余地，整个车辆只是利用后轮的补偿在跟踪目标角速度，不能完全发挥四轮转向的优势。因此本文对上述策略进行进一步改进，引入模糊推理下的前轮和后轮转角补偿的联合控制方法来对转弯操稳性进行控制。系统框图见图4。

图3 模糊PID控制

图4 前后轮补偿的模糊控制框图

该方法利用输入的角速度误差及其变化率并结合自定义的模糊规则库来计算前轮和后轮需要增减的角度，实现车轮转角的动态补偿。同时前后轮转向比依据车体前后轴到质心的距离比确定，可以在运动学层面消除质心侧偏角。设置误差范围为[−2,2]，量化因子为0.5，误差变化率的范围为[−5,5]，量化因子为0.2。前后轮转角的补偿值论域均为[−0.174 5,0.174 5]，比例因子为1。输入和输出的隶属度函数为三角函数。图5为输入的隶属度函数和模糊变量取值。前后轮转角范围为±35°。隶属度等级从负大至正大依次以字符串NB，NM，NS，NZ，ZO，PZ，PS，PM和PB表示。

图5 误差隶属度函数

图6和图7为输入误差变化率的隶属度函数和输出前后轮补偿转角的隶属度函数。隶属度等级从负大至正大依次以字符串NB，NM，NS，ZO，PS，PM和PB表示。输出补偿转角的隶属度等级从减大至增大依次以字符串NB，NM，NS，ZO，PS，PM和PB表示。规定轮胎转向角逆时针转向为正，顺时针转向为负。

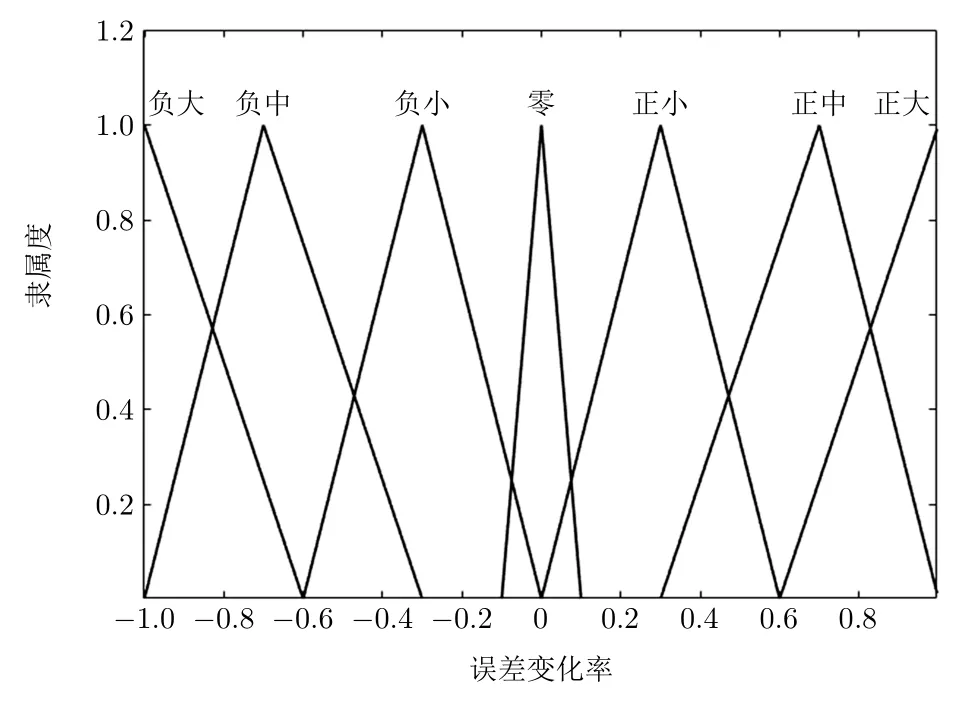
图6 输入误差变化率的隶属度函数

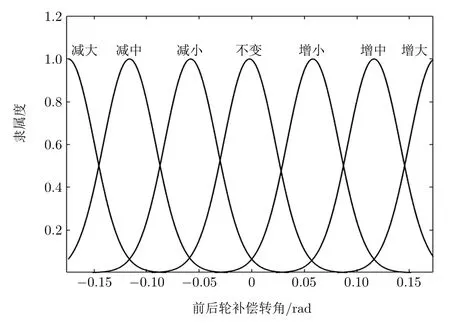
图7 输出补偿转角的隶属度函数

根据If (E is A) and (EC is B) then (U is C)的原则写出63 条模糊规则。其中E 为误差，EC 为误差变化率，U为输出，这里为前后轮的补偿转向角。当角速度大于预设值且有继续增大的趋势时，就减小前后轮转角，以降低横摆率。反之增大转向角以提高横摆率的增速。转角增减的幅度依据误差和误差变化率的大小及正负来动态调整。经过反复仿真调试，得到较为合理的模糊推理关系。图8为前轮转角补偿模糊控制规则，图9为后轮转角补偿模糊控制规则。图8和图9中第一行为误差变化率等级，第一列为误差等级，其余内容为对应前后轮转角补偿量的等级。

图8 前轮转角补偿模糊控制规则

图9 后轮转角补偿模糊控制规则

4 基于模糊控制的仿真分析

根据式（6）和式（7），结合拉普拉斯变换中的终值定理可以推出稳态横摆角速度增益P，见式（17）。稳定因数K 见式（18）。

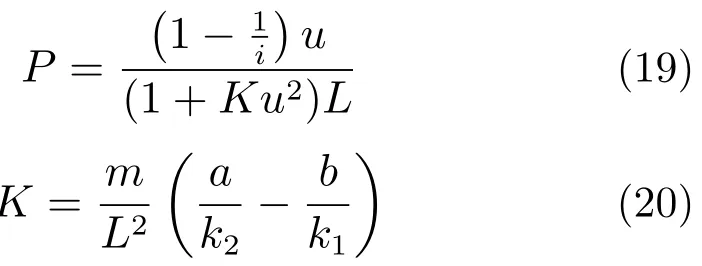
仿真参数设置：前轮转角为15°，前后轮采用前馈比例控制，其转动比为0.263 3，车辆的转弯时速为22.35 m/s，稳态增益2.456 7。稳态横摆角速度为0.643 2 rad/s，在得到车辆实际的横摆角速度误差和误差变化率后，模糊控制器会通过模糊推理得到需要补偿的前后轮转角，再利用转向伺服系统去跟踪这一补偿转角的信号，最终实现对车辆横摆角速度的控制。线控转向伺服电机控制的主要目的是使各车轮具有更加灵活、精确的转角控制和动态调整性。仿真选择的电机参数设置：额定电压48 V，电机转矩系数0.203 N·m/A，电枢电阻0.027 Ω，电感系数0.195 mH，额定转速2 000 r/min，额定电流31.5 A，转子惯量0.001 87 kg·m2。电机转角控制策略为3个闭环控制的伺服转向电机系统[10]，如图10所示。

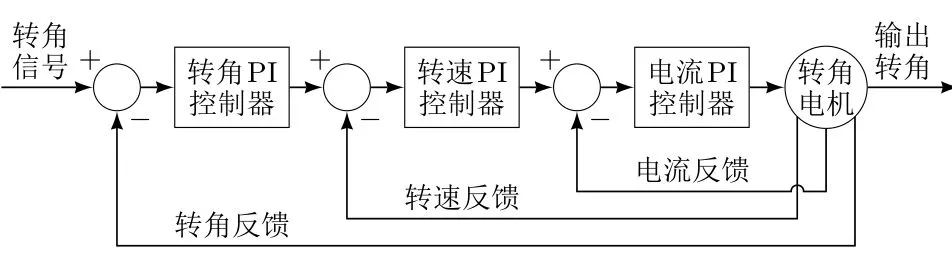
图10 伺服电机系统

将模糊补偿后的前后轮转角信号输入伺服转向系统后由电机来完成最终的转向操作。图11分别给出了模糊推理机控制下和前馈比例控制下的横摆角速度响应曲线[11]，图12分别给出了模糊推理机控制下和前馈比例控制下的质心侧偏角响应曲线。

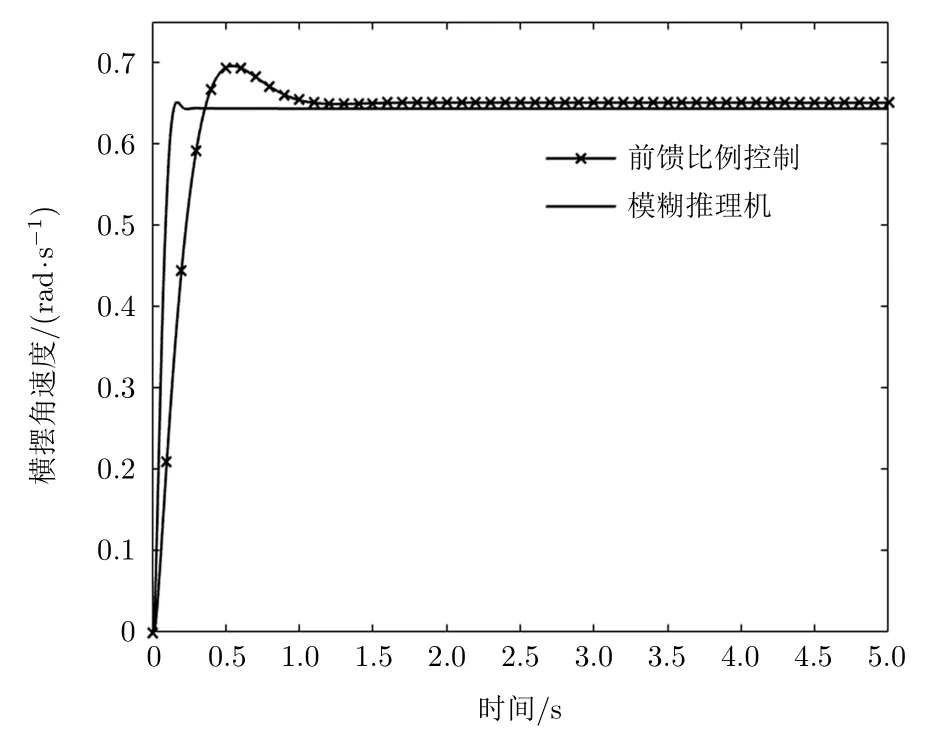
图11 横摆角速度响应

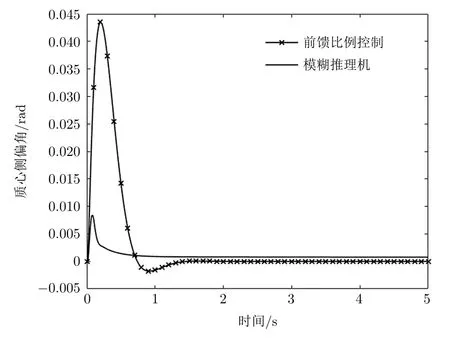
图12 质心侧偏角响应

5 结束语

通过对比前馈比例控制下的四轮转向系统和模糊推理机控制下的四轮转向补偿系统在转弯时的操稳性仿真结果，可得以下结论：

1）模糊推理下的前后轮转向控制系统可以降低动力学引起的横摆率偏差，控制前的横摆角速度超调量为0.052 4 rad/s，反应时间0.385 9 s。控制后的超调量为0.008 1 rad/s，反应时间0.258 2 s，在提高快速性的同时能显著降低横摆角速度的超调量，具有较强的稳定性。

2）控制前最大质心侧偏角超调量为2.492 4°，控制后超调量为0.481 3°。相比前馈比例转向控制的四轮转向系统，模糊推理系统能减小车辆转弯时质心侧偏角响应的稳定时间和超调量，提高了车辆转弯的操稳性，实现了对传统前馈比例转向控制策略的优化。